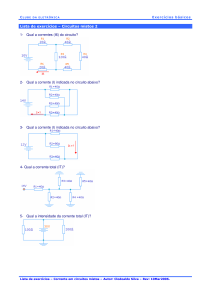
Circuitos RLC - Eletronica Basica
Anuncio
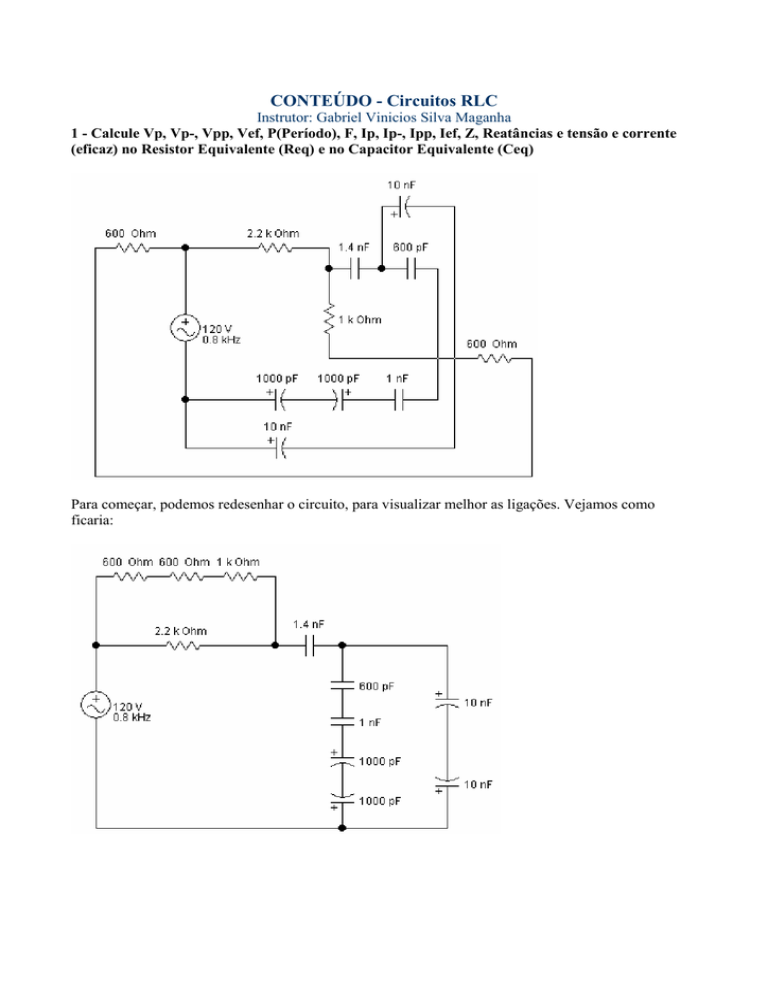
CONTEÚDO - Circuitos RLC Instrutor: Gabriel Vinicios Silva Maganha 1 - Calcule Vp, Vp-, Vpp, Vef, P(Período), F, Ip, Ip-, Ipp, Ief, Z, Reatâncias e tensão e corrente (eficaz) no Resistor Equivalente (Req) e no Capacitor Equivalente (Ceq) Para começar, podemos redesenhar o circuito, para visualizar melhor as ligações. Vejamos como ficaria: Vamos agora resolver as associações de resistores e capacitores, para encontrar Req e Ceq: Ra = 600 + 600 + 1K = 2,2 KOhm Req = 2,2K Ohm em paralelo com 2,2 KOhm -> Req = 1,1KOhm Ca = 1 1 1 1 1 + + 600 p 1n 1000 p 1000 p ⇒ Ca = 214,285 pF Cb = 10nF / 2 -> Cb = 5nF Ceq = 1 1 1 + 214,285 p 5n ⇒ Ceq = 205,478 pF Portanto, o circuito fica: Calculemos, então, a oposição que o capacitor oferece à passagem da AC, a Reatância Capacitiva (Xc): Xc = 1 ⇒ Xc = 968,690Ω 6,28.0,8k .205,478 p O circuito então fica: Falta agora apenas calcularmos a Impedância (Z): Z = 1.1k ² + 968,690² ⇒ Z = 1465,728Ω Conhecemos a Tensão total e também a Impedância do circuito. Podemos calcular a Corrente Total: It = 120 / 1465,73 -> It = 81,87mA Voltando ao circuito anterior, com a Resistência e a Reatância: IReq = 81,87mA Req = 1,1 KOhm Vreq = 90,057V Ic = 81,87mA Xc = 968,69 Ohm Vc = 79,306 V Só não podemos nos esquecer dos outros cálculos: Vef = 120V Vp = 120 . 1,414 -> Vp = 169,68V Vp- = -169,68V Vpp = 339,36 V Ief = 81,87mA Ip = 81,87 . 1,414 -> Ip = 115,764mA Ip - = 115,764mA Ipp = 231,528 mA P = 1 / 0.8k -> P = 1,25ms 2 - Calcule XL, R, Z, It, IR, IL, VL, VR, Vf (Tensão do Gerador), F e P (Período): Circuito série -> Corrente é a mesma. IR = IL = 350mA Calculemos então a tensão no Resistor: VR = 200 x 350m -> VR = 70V Quanto ao indutor, sabemos sua tensão e sua corrente. Podemos calcular sua reatância indutiva: XL = 105 / 350m -> XL = 300 Ohm Podemos aproveitar que conhecemos as tensões de VR e VL para calcular VF: Vf = 70² + 105² ⇒ Vf = 126,194V Se sabemos It e Vf, podemos, por lei de Ohm, descobrir a Impedância (Z) do circuito: Z = 126,194 / 350m -> Z = 360,55 Ohm Agora, falta apenas calcularmos a Frequência e o Período do Sinal. Repare: Nós já sabemos tudo sobre o Indutor, exceto a freqüência. Invertendo a fórmula, podemos encontrá-la. Vejamos: XL = 6,28.F .L ⇒ F = XL 6,28.L Assim: F= 300 = 612,444 Hz 6,28.78mH Agora ficou fácil calcular o período: P = 1 / 612,444 -> P = 1,6328 ms 3 - Calcule Z, It, IR e IL: XL = 6,28.0,8k.23m -> XL = 115,552 Ohm Z= 1 1 1 + 200² 115,552² ⇒ Z = 100,053Ω It = 120 / 100,053 -> It = 1,199A Calculando IR: IR = 120 / 200 -> IR = 600mA Calculando IL: IL = 120 / 115,552 -> IL = 1,038 A Podemos inclusive tirar a prova real: It = 600mA² + 1,038² ⇒ It = 1,199 A Portanto, a conta bate. 4 - Considerando a Freqüência do sinal do gerador como 1700 Hz e a tensão do gerador de 339,412Vpp, calcule a Impedância e as correntes do circuito abaixo: XL = 6,28 x 1700 x 23m -> XL = 245,548 Ohm Xc = 1 / (6,28 x 1700 x 780n) -> Xc = 120,087 Ohm R = 200 Ohm Z= 1 1 1 1 + − ² 200² 245,548 120,087 ⇒ Z = 152,316Ω Se Vpp é 339,412, então Vp e Vp- serão a metade: 169,706V Assim, Vef será: Vef = 169,706 / 1,414 -> Vef = 120V Sabendo a tensão do gerador e a impedância do circuito, conseguimos encontrar a corrente total: It = 120 / 152,316 -> It = 787,836 mA Vamos tirar a prova, calculando a corrente de cada um dos componentes individualmente e depois encontrando, a partir deles, o valor de It: IR = 120/200 -> IR = 600mA IL = 120 / 245,548 -> IL = 488,703 mA IC = 120 / 120,087 -> IC = 999,276 mA Agora, vamos ver se o It bate com o que calculamos logo acima: It = 600mA² + (999,276m − 488,703m)² ⇒ It = 787,836mA Portanto, comprovamos as fórmulas e os cálculos. 5 - A impedância de um circuito RC paralelo ligado em um gerador AC é 600 Ohms, enquanto que o valor do Resistor é de 1K Ohm. Calcule, a partir desses valores, qual é a reatância capacitiva do capacitor. Para fazermos o calculo, devemos isolar Xc da fórmula da impedância. Eis a fórmula original de Z do circuito RC paralelo: Z= Xc ² = 1 1 1 + R ² Xc ² 1 1 1 − Z ² R² → 1 = Z → Xc = 1 1 1 1 1 1 1 1 1 1 1 + → ² = + → = + → − = R ² Xc ² R ² Xc ² Z ² R ² Xc ² Z ² R ² Xc ² Z 1 1 1 − Z ² R² Assim, a conta ficará: Xc = 1 1 1 − 600² 1000² → Xc = 750Ω Vamos tirar a prova, para ver se realmente acertamos? 1 Z= 1 1 + R ² Xc ² → Z = 1 1 1 + 1000² 750² → 600Ω Perfeito! 6 - Quanto ao exercício anterior, digamos que o valor desse capacitor seja de 800 pF. Qual será, então, o período do sinal do circuito? Para sabermos o período, temos de ter a freqüência. Basta, então, isolarmos F na fórmula da Reatância Capacitiva: Xc = 1 1 1 → Xc.6,28.C = → F = 6,28.F .C F Xc.6,28.C E aplicá-la: F= 1 → F = 265,393Hz 750.6,28.800 p E encontrar o Período: P = 1 / 265,393 -> P = 3,768 us ou 3,768E-6s Dicas para a prova: Não esquecer que capacitores e indutores defasam a corrente ou a tensão em 90º no circuito. Portanto, as leis de Kirchoff podem ser aplicadas, mas sempre se usando soma vetorial e não soma algébrica. Isso significa que: - No circuito série, a corrente sempre será a mesma e as tensões serão encontradas se efetuarmos a soma vetorial (Pitágoras) delas. - No circuito paralelo, a tensão sempre será a mesma e as correntes serão encontradas se efetuarmos a soma vetorial delas. Portanto, as fórmulas são intuitivas e pouco esforço é necessário para entendê-las. Um abraço, fiquem com Deus, Gabriel.