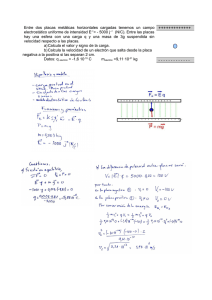
Desarrollo de ecuaciones y efecto de los concentradores de
Anuncio

UNIVERSIDAD SIMÓN BOLÍVAR DECANATO DE ESTUDIOS PROFESIONALES COORDINACIÓN DE INGENIERÍA DE MATERIALES DESARROLLO DE ECUACIONES Y EFECTO DE LOS CONCENTRADORES DE ESFUERZOS SOBRE LAS PROPIEDADES MECÁNICAS Realizado por: Joel Alfredo Campero Tiberio INFORME FINAL DE CURSOS EN COOPERACIÓN Presentado ante la ilustre Universidad Simón Bolívar como requisito parcial para optar al título de Ingeniero de Materiales Opción: Polímeros Sartenejas, octubre de 2007 UNIVERSIDAD SIMÓN BOLÍVAR DECANATO DE ESTUDIOS PROFESIONALES COORDINACIÓN DE INGENIERÍA DE MATERIALES DESARROLLO DE ECUACIONES Y EFECTO DE LOS CONCENTRADORES DE ESFUERZOS SOBRE LAS PROPIEDADES MECÁNICAS LABORATORIO “E” SECCIÓN DE POLÍMEROS UNIVERSIDAD SIMÓN BOLÍVAR TUTOR INDUSTRIAL: Ing. Héctor Rojas TUTOR ACADÉMICO: Prof. María Virginia Candal JURADO EVALUADOR: Prof. Miren Ichazo Sartenejas, octubre de 2007 UNIVERSIDAD SIMÓN BOLÍVAR DECANATO DE ESTUDIOS PROFESIONALES COORDINACIÓN DE INGENIERÍA DE MATERIALES ACTA FINAL DE PROYECTO DE GRADO DESARROLLO DE ECUACIONES Y EFECTO DE LOS CONCENTRADORES DE ESFUERZOS SOBRE LAS PROPIEDADES MECÁNICAS Presentado por: Joel Alfredo Campero Tiberio Este proyecto ha sido examinado por el siguiente jurado: ______________________________ Prof. María Virginia Candal (Tutor Académico) ______________________________ Ing. Héctor Rojas (Tutor Industrial) ______________________________ Prof. Miren Ichazo (Jurado Evaluador) Sartenejas, octubre de 2007 DESARROLLO DE ECUACIONES Y EFECTO DE LOS CONCENTRADORES DE ESFUERZOS SOBRE LAS PROPIEDADES MECÁNICAS Realizado por: Joel Alfredo Campero Tiberio RESUMEN El objetivo principal del presente trabajo consistió en el estudio de la influencia que presentan los concentradores de esfuerzos sobre las propiedades mecánicas de piezas plásticas inyectadas. Para esto cuatro geometrías distintas de entallas fueron evaluadas (triangular, rectangular, semicircular y circular) y finalmente, fue desarrollado un modelo de ecuación constitutiva para la obtención del factor Kt a través de herramientas CAD/CAE. Para esto inicialmente se realizó un análisis mediante el criterio de la convergencia, con la finalidad de que los resultados obtenidos por medio del programa simulador C-MOLD fuesen válidos. Seguidamente se llevaron a cabo simulaciones del proceso de inyección y ensayos mecánicos de tracción a placas de Poliestireno de Alto Impacto (PSAI), en donde se variaron las dimensiones del concentrador presente en cada caso, para luego realizarse las curvas del factor Kt en función de las relaciones geométricas d/D y r/d. A continuación se procedió al estudio de diferentes condiciones de operación (temperaturas del fundido y refrigerante, presión sostenida y velocidad de inyección), así como a la verificación de su influencia sobre el factor Kt. Igualmente para este caso, se elaboraron curvas para el factor Kt en función de la variable estudiada. Por último, un modelo de ecuación constitutiva fue desarrollado con el propósito de calcular un factor Kt teórico, así mismo, los valores obtenidos a través de este método fueron comparados con los conseguidos a través de las simulaciones, lográndose resultados coherentes y con un alto grado de validez, en donde para la mayor parte de los resultados se obtuvieron errores menores al 10%. Se verificó que el factor Kt es dependiente tanto de los parámetros geométricos, como de las condiciones de operación utilizadas, en donde para estas últimas se tiene que el factor Kt disminuye con el aumento tanto de la temperatura del fundido como de la temperatura del refrigerante, mientras que es incrementado a magnitudes mayores de presión sostenida. Por su parte, la velocidad de inyección es la variable que menos influencia presenta sobre este factor. ii A todas las personas que de una u otra manera siempre permanecieron a mi lado, apoyándome, dándome fuerzas y brindándome su amistad. “Aprendí… que uno nunca puede marchar hacia atrás, que no debería intentarse siquiera, que la esencia de la vida es ir hacia delante. La vida es, en realidad, una calle de sentido único”. Agatha Christie. “Quedarse en lo conocido por miedo a lo desconocido, equivale a mantenerse con vida pero no vivir”. Anónimo. iii AGRADECIMIENTOS A Dios, por acompañarme en cada momento de mi vida, protegiéndome, guiándome e iluminándome con su gracia. A mi Papá, mi Mamá y mi Hermana, quienes me han brindado todo su cariño, apoyo incondicional y confianza durante toda mi vida y que sin ellos, ninguno de mis logros hubiese sido posible. A toda mi familia y especialmente a mis abuelos, por ayudarme en cada momento en que los he necesitado y por esas palabras de aliento que llenan el corazón. A mi tutora María Virginia, quien más que una profesora, es un ángel que Dios envió a la tierra para guiarnos en nuestro camino y quien finalmente se convirtió en una amiga. A mi tutor Héctor Rojas, por siempre estar dispuesto a colaborar en mi trabajo y a encontrar las soluciones más viables a los problemas presentados. A todos mis profesores, quienes cada uno a su manera nos enseñaron el mundo de los polímeros, ese mundo que años atrás, ni siquiera sabíamos que existía. A mis queridos amigos polimeristas, Daniel, Kiri, Tutu, Ibra, Heli, Emira, Beto, Elizabeth, Marce, Rodo, Conde, Miguel, Angélica y todos aquellos con quienes pasé los mejores momentos de mi vida. Gracias por brindarme su amistad y por ser tan especiales como lo son. A mis amigos de toda la vida, Carlos, David, Ligia, Darwin, María, Oriella, Guille, Colombia, Joubert, Adri y Sheila, por permanecer a mi lado todo este tiempo y ser parte de mi vida. Finalmente, a todas las demás personas que de una u otra manera tocaron mi vida y permitieron que hoy por hoy, pueda ser la persona que soy. iv ÍNDICE GENERAL RESUMEN ii DEDICATORIA iii AGRADECIMIENTOS iv ÍNDICE GENERAL v ÍNDICE DE TABLAS vii ÍNDICE DE FIGURAS viii CAPÍTULO I: INTRODUCCIÓN 1 CAPÍTULO II: OBJETIVOS 3 CAPÍTULO III: MARCO TEÓRICO 5 3.1 Moldeo por Inyección 5 3.2 Propiedades Mecánicas 8 3.3 Concentradores de Esfuerzos 11 3.4 Herramientas de Diseño y Simulación de Procesos en Piezas Plásticas 14 3.5 Antecedentes 20 3.6 Justificación del Proyecto 22 CAPÍTULO IV: METODOLOGÍA 23 4.1 Revisión Bibliográfica 23 4.2 Diseño y Mallado Preliminar de las Placas en el Programa Modelador 24 Pro-ENGINEER 4.3 Montaje de los Sistemas en C-MOLD 26 4.4 Determinación del Número de Nodos Óptimo mediante el empleo 30 del Criterio de la Convergencia 4.5 Simulación del Proceso de Inyección y del Ensayo de Tracción, 31 para diferentes geometrías de Entallas y Variación de las Condiciones de Operación en C-MOLD 4.6 Determinación del Parámetro de Concentración de Esfuerzos 33 4.7 Desarrollo de una Metodología para la realización de Ecuaciones 34 Constitutivas CAPÍTULO V: DISCUSIÓN DE RESULTADOS 5.1 Criterio para la Convergencia de resultados en Simulaciones realizadas 36 36 bajo sistemas CAD/CAE 5.2 Determinación del factor de Concentración de Esfuerzos (Kt) v 45 5.3 Influencia de la Geometría de las entallas sobre el Factor de Concentración 49 de Esfuerzos (Kt) 5.3.1 Entallas Triangulares 50 5.3.2 Entallas Circulares 52 5.3.3 Entallas Semicirculares 53 5.3.4 Entallas Rectangulares 55 5.4 Influencia de las Condiciones de operación sobre el Factor de Concentración 57 de Esfuerzos (Kt) 5.4.1 Temperatura del Fundido 57 5.4.2 Presión Sostenida 60 5.4.3 Velocidad de Inyección 62 5.4.4 Temperatura del Refrigerante 64 5.5 Desarrollo de una Metodología y Elaboración de Ecuaciones para el Factor 66 de Concentración de Esfuerzos (Kt) 5.5.1 Revisión Bibliográfica 66 5.5.2 Elaboración de gráficas tipo Arrhenius para las Temperaturas del 68 Fundido y del Líquido Refrigerante 5.5.3 Obtención de las Expresiones Cuadráticas resultantes de cada una de 69 las relaciones graficadas para el Factor Kt, como función de las distintas condiciones evaluadas 5.5.4 Desarrollo de Expresiones Cuadráticas e Iteraciones, mediante el 70 empleo del Software ORIGIN CAPÍTULO VI: CONCLUSIONES Y RECOMENDACIONES 76 CAPÍTULO VII: REFERENCIAS BIBLIOGRÁFICAS 81 APÉNDICES 88 vi ÍNDICE DE TABLAS Tabla 4.1 Dimensiones empleadas para concentradores de esfuerzos triangular 25 y rectangular. Tabla 4.2 Dimensiones empleadas para concentradores de esfuerzos circular 26 y semicircular. Tabla 4.3 Propiedades de la resina empleada para las simulaciones en C-MOLD. 32 Tabla 4.4 Condiciones de operación utilizadas para las distintas simulaciones 33 realizadas. Tabla 5.1 Resultados adicionales estudiados para el criterio de la convergencia, en un 41 concentrador de esfuerzos de tipo semicircular. Tabla 5.2 Resultados adicionales estudiados para el criterio de la convergencia, en un 41 concentrador de esfuerzos de tipo triangular. Tabla 5.3 Magnitudes correspondientes a cada constante expresada en la ecuación constitutiva para los diferentes concentradores de esfuerzo estudiados. vii 72 ÍNDICE DE FIGURAS Figura 3.1 Representación de una máquina de inyección. 5 Figura 3.2 Ventana de procesabilidad para polímeros. 7 Figura 3.3 Máquina para ensayos de tracción. 8 Figura 3.4 Curcas típicas para ensayos de esfuerzo-deformación: (a) Fractura frágil, 9 (b) Fractura dúctil, (c) Formación de un cuello (punto de fluencia) y (d) Elastómeros. Figura 3.5 Tipos de concentradores de esfuerzos: (a) entalla triangular o tipo cuña, 12 (b) entalla semicircular, (c) entalla rectangular, (d) cambio de sección o tipo hombro, (e) entalla semicircular que finaliza con lados rectos y (f) agujero. Figura 3.6 Gráficas con los respectivos valores de Kt para barra rectangular metálica 13 con diferentes concentradores de esfuerzos: (a) tipo hombro, (b) entalla en forma de “U” y (c) agujero. dominio: 15 Figura 3.8 Ciclo de diseño y fabricación de un producto mediante la utilización de 18 Figura 3.7 Métodos numéricos para la representación de un (a) MEF y (b) MDF. herramientas CAD/CAE/CAM. Figura 4.1 Placas diseñadas en Pro-ENGINEER con sus dimensiones principales: 25 (a) Triangular, (b) Rectangular, (c) Circular y (d) Semicircular. Figura 4.2 Mallas realizadas a placas con entallas: (a) Triangular, (b) Rectangular, 26 (c) Circular y (d) Semicircular. Figura 4.3 Sistema empleado para las simulaciones correspondientes a la placa con 27 entalla triangular en C-MOLD. Figura 4.4 Sistema empleado para las simulaciones correspondientes a la placa con 28 entalla rectangular en C-MOLD. Figura 4.5 Sistema empleado para las simulaciones correspondientes a la placa con 28 entalla circular en C-MOLD. Figura 4.6 Sistema empleado para las simulaciones correspondientes a la placa con 28 entalla semicircular en C-MOLD. Figura 4.7 Fuerza nodal establecida en una de las placas estudiadas. 29 Figura 4.8 Restricciones establecidas en una de las placas estudiadas. 30 viii Figura 4.9 Placas con entalla circular y diferente número de nodos: (a) 10 nodos, 31 (b) 40 nodos y (c) 80 nodos. Figura 4.10 Detalle de los valores de esfuerzo tomados en la zona de la entalla 34 (Esfuerzo de Mises-Hencky para cargas de servicio). Figura 5.1 Resultados analizados para el criterio de convergencia de la entalla 38 semicircular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. Figura 5.2 Resultados analizados para el criterio de convergencia de la entalla 39 circular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. Figura 5.3 Resultados analizados para el criterio de convergencia de la entalla 39 rectangular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. Figura 5.4 Resultados analizados para el criterio de convergencia de la entalla 40 triangular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. Figura 5.5 Resultados utilizados para el estudio del criterio de la convergencia en 42 placas con concentradores de esfuerzos triangulares. Figura 5.6 Otros resultados utilizados para el estudio del criterio de la convergencia 43 en placas con concentradores de esfuerzos triangulares. Figura 5.7 Distribución de esfuerzos en placas con entallas semicirculares y diferentes 47 relaciones d/D: (a) 0.92, (b) 0.88, (c) 0.85, (d) 0.81, (e) 0.78, (f) 0.74, (g) 0.71 y (h) 0.67. Figura 5.8 Esquema de distribución de esfuerzos de Mises-Hencky en una placa 48 entallada. Figura 5.9 Verificación de tendencias descritas por los esfuerzos en el procesamiento, 48 cargas de servicio y resultante. Figura 5.10 Curvas obtenidas para placas con entallas triangulares del factor Kt en 50 función de: (a) d/D y (b) r/d. Figura 5.11 Curva obtenida para placas con entallas circulares del factor Kt en 52 función de d/D. Figura 5.12 Esfuerzos registrados en placas con entallas circulares de diámetro: (a) 7 mm y (b) 28 mm. ix 52 Figura 5.13 Distribución de esfuerzos alrededor de un agujero situado en una placa 53 delgada infinita. Figura 5.14 Curvas obtenidas para placas con entallas semicirculares del factor Kt en 54 función de: (a) d/D y (b) r/d. Figura 5.15 Curvas obtenidas para placas con entallas rectangulares del factor Kt en 55 función de: (a) d/D y (b) r/d. Figura 5.16 Disposición de los esfuerzos de Mises-Hencky medidos en las placas con 56 entallas rectangulares. Figura 5.17 Curvas de Kt obtenidas en función de la temperatura del fundido para 58 entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Figura 5.18 Líneas de soldadura en placas con entallas circulares para distintas 60 temperaturas del fundido: (a) 190 °C y (b) 270 °C. Figura 5.19 Curvas de Kt obtenidas en función de la presión sostenida para entallas de 61 tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Figura 5.20 Curvas de Kt obtenidas en función de la velocidad de inyección para 63 entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Figura 5.21 Curvas de Kt obtenidas en función de la temperatura del líquido 65 refrigerante para entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Figura 5.22 Ln (Kt) en función de 1/T refrigerante, para una placa con entalla 69 semicircular. Figura 5.23 Relaciones graficadas para placas con entallas semicirculares y 70 coeficientes importantes. Figura 5.24 Pasos para el establecimiento de un modelo de ecuación cuadrática en 71 ORIGIN: (a) Introducción de datos, (b) Módulo para sistemas no lineales y (c) Ecuación cuadrática genérica. Figura 5.25 (a) Establecimiento de valores iniciales en ORIGIN y (b) Iteraciones. 71 Figura 5.26 Factor de concentración de esfuerzos obtenido de manera simulada y 73 teórica para placas con entallas de tipo: (a) Triangular, (b) Rectangular, (c) Circular y (d) Semicircular. x CAPÍTULO I INTRODUCCIÓN A través de los últimos años la industria del plástico ha cobrado una importancia significativa en cuanto a la elaboración de productos basados en este material para muy diversos campos como lo pueden ser las industrias automovilística, aeronáutica, farmacéutica, de uso general, etc. Así mismo, la preferencia de piezas elaboradas de plástico en comparación a las metálicas o cerámicas se fundamenta principalmente en las tan atractivas propiedades de este material en cuanto a bajo peso y costo, translucidez, propiedades no corrosivas, entre otras. Los esfuerzos existentes en piezas con geometría constante sometidas a cargas (por ejemplo tracción), pueden ser determinados con una relativa simplicidad mediante el empleo de diferentes técnicas experimentales o teóricas, sin embargo cuando la pieza presenta variaciones en su geometría, el cálculo de estos esfuerzos puede ser considerablemente más complicado. A raíz de esto es importante tener en consideración que, al momento de diseñar y analizar cualquier tipo de pieza, en su mayoría éstas tendrán secciones transversales variables, producto de la existencia de entallas, agujeros y cualquier otro tipo de discontinuidades, las cuales de una manera u otra influyen sobre las propiedades de la pieza en cuestión, especialmente en sus propiedades mecánicas. Estas interrupciones en la sección transversal producirán concentraciones de esfuerzos que consecuentemente reducirán la resistencia mecánica del producto. Estas concentraciones de esfuerzos son especialmente significativas en piezas elaboradas de material plástico, debido a que son puntos altamente sensibles durante el proceso de transformación, haciendo posible tanto que el material pueda degradarse en las zonas circundantes a estas localidades, así como que se magnifique la concentración de esfuerzos. El parámetro utilizado para evaluar la intensidad de esfuerzos es conocido como factor de concentración de esfuerzos (Kt) y éste depende principalmente de la geometría de la discontinuidad presente en la pieza. Estudios recientes para plásticos indican que debido a 2 factores como la naturaleza visco-elástica, la baja conductividad térmica y otros factores intrínsecos del material, provocan que el coeficiente Kt dependa igualmente de las condiciones de fabricación o moldeo. Es necesario destacar que los diseñadores de piezas tanto metálicas como plásticas utilizan en sus cálculos magnitudes de Kt, que corresponden a una serie de curvas presentes en la literatura que han sido calculadas únicamente para metales. Por este motivo, al diseñar una pieza plástica solamente se está realizando una aproximación de la posible concentración de esfuerzos que se puede encontrar en ésta y no hallando un valor preciso para un diseño veraz. En vista de lo anterior, el objetivo de este trabajo será la construcción de curvas correspondientes al factor Kt para diferentes formas y geometrías de entallas concentradoras de esfuerzos, a la vez de que se pretende corroborar y especificar lo más posible la influencia que tiene la variación de las condiciones de operación en el proceso de inyección sobre este factor. Se trabajará con un Poliestireno de Alto Impacto (PSAI) y los concentradores de esfuerzos a utilizar serán: circular, triangular, rectangular y semicircular. Así mismo, este estudio será realizado mediante la aplicación de herramientas de diseño y simulación CAD/CAE, teniendo especial cuidado en el número de nodos empleados para cada caso con la finalidad de obtener la mayor convergencia posible entre los resultados; de esta manera, los resultados serán lo más parecidos a la realidad. El programa simulador a emplear será C-MOLD 2000, con el cual será posible obtener toda la información correspondiente a los esfuerzos en cargas de servicio y en procesamiento, resultantes de los ensayos de tracción para cada tipo de concentrador en particular, con los que se construirán las curvas de Kt y se desarrollarán modelos de ecuaciones constitutivas. Finalmente, en vista de la importancia que conlleva el estudio de la concentración de esfuerzos en todo tipo de piezas y de la falta de información pertinente al área de los polímeros, se ha decidido llevar a cabo este trabajo, de manera tal que se pueda constituir un precedente y una metodología para próximas investigaciones, además de establecer criterios y tendencias que describan el comportamiento de piezas plásticas bajo los efectos de diversas variables. CAPÍTULO II OBJETIVOS OBJETIVO GENERAL Estudio del factor de concentración de esfuerzos (Kt) en piezas plásticas inyectadas, mediante la utilización de herramientas de diseño CAD/CAE y modelos teóricos. OBJETIVOS ESPECÍFICOS • Evaluar la influencia que presentan los concentradores de esfuerzos de tipo rectangular, triangular, circular y semicircular, sobre las propiedades mecánicas de piezas inyectadas de PSAI mediante el empleo del software de simulación C-MOLD. • Estudiar la influencia de las condiciones de inyección (temperaturas del fundido y refrigerante, presión sostenida y velocidad de inyección) sobre las propiedades mecánicas de piezas inyectadas de PSAI simuladas en C-MOLD. • Determinar la magnitud del factor de concentración de esfuerzos Kt modificando la geometría de los concentradores y las condiciones del proceso de inyección (temperaturas del fundido y refrigerante, presión sostenida y velocidad de inyección). • Obtener las curvas características correspondientes a Kt, en función de los parámetros geométricos d/D y r/d para los concentradores triangular, rectangular, semicircular y circular, manteniendo las condiciones de operación constantes. • Obtener las curvas características correspondientes a Kt, mediante la variación de la presión sostenida, la velocidad de inyección y las temperaturas del fundido y del líquido refrigerante, manteniendo la geometría del concentrador de esfuerzos constante. • Estudiar el efecto del número de elementos sobre la convergencia de los resultados de llenado, enfriamiento y contracción reportados por el programa C-MOLD. 4 • Establecer una metodología para la elaboración de ecuaciones constitutivas relacionadas con el efecto de las variables del proceso de inyección y la geometría de la entalla sobre el factor Kt. • Desarrollar ecuaciones constitutivas para el factor Kt que incluyan tanto la geometría de las distintas entallas, así como los diferentes parámetros de inyección estudiados. CAPÍTULO III MARCO TEÓRICO 3.1 MOLDEO POR INYECCIÓN El moldeo por inyección es el principal proceso de transformación de plásticos encontrado en la industria, abarcando cerca del 50 % de esta. Este proceso es idealmente utilizado para elaborar piezas que requieran de una gran precisión dimensional, así como que tengan formas complejas (piezas electrónicas y médicas, partes para la industria automotriz, componentes para la construcción, etc.). Básicamente, éste es un proceso automatizado y en continuo que es desarrollado a alta velocidad, con el que se pueden elaborar gran cantidad de piezas utilizando casi cualquier material (termoplásticos, termoestables, elastómeros) [1-3]. El ciclo para este proceso de transformación da comienzo una vez cerrado el molde, seguido de la inyección del plástico fundido a la cavidad. Una vez la cavidad o las cavidades del molde son llenadas, es aplicada una presión de sostenimiento con el objetivo de compensar la contracción final de la pieza; simultáneamente el tornillo gira para cargar el material necesario para la próxima inyección. Por último, una vez enfriada la pieza, el molde se abre y ésta es expulsada proceso se encuentra [3] . Se puede decir entonces que en términos muy generales este comprendido por dos grandes etapas principales, la primera que corresponde al fundido del material plástico en estado sólido, mezclado, presurización y flujo, todo lo cual ocurre en la unidad de moldeo de la máquina de inyección, mientras que en la segunda etapa el material se encuentra dentro del molde de inyección, en donde será enfriado y tomará la forma final [4-5] . Seguidamente, en la figura 3.1 se puede observar una representación de una máquina de inyección con sus componentes y zonas principales. Figura 3.1 Representación de una máquina de inyección [6]. 6 Es importante mencionar que de todas las variables involucradas en el proceso de inyección, las más resaltantes son [1, 3, 5-9]: • Presión de Inyección: este parámetro puede variar ampliamente dependiendo del tamaño y tipo de máquina empleada, así como de la forma del molde. Esta corresponde a la presión que es ejercida sobre el material fundido que se encuentra en la parte frontal del tornillo durante la etapa de inyección, y afecta tanto la velocidad de avance del tornillo, como la entrada del material a la cavidad del molde. • Presión Sostenida: ésta es aplicada sobre el material fundido, y tiene como finalidad la de compensar los posibles efectos de contracción y alabeo al enfriarse la pieza. Por lo general, esta presión se ejerce hasta que la entrada se solidifica, debido a que luego de esto el polímero fundido ya no podrá entrar ni salir de la cavidad. • Tiempo de Presión Sostenida: corresponde al intervalo de tiempo durante el cual la presión sostenida es aplicada. • Velocidad de Inyección: es la velocidad con la cual es inyectado el material fundido a la cavidad del molde. Ésta es dependiente de factores como la viscosidad del fundido, la temperatura y condiciones del molde, tamaño y número de entradas de material, entre otras. Con la efectiva variación de este parámetro es posible obtener acabados brillantes en las piezas, así como corregir una serie de defectos superficiales. • Temperatura del Fundido: esta variable es de mucha importancia, debido a que es la que determina las propiedades estructurales de las piezas moldeadas. En vista de esto, debe mantenerse uniforme y constante al llegar a la zona de la boquilla, ya que de esto dependerá la densidad y contracción final obtenida. • Temperatura del Molde: esta temperatura se encuentra determinada por el material que va a ser procesado y presenta una fuerte influencia tanto en la productividad como directamente en las propiedades de las piezas moldeadas (calidad superficial, grado de cristalinidad, orientación, etc.). 7 • Tiempo de Ciclo: es el tiempo necesario para que se realicen todas las etapas del proceso de inyección. Éste involucra los tiempos de apertura y cierre del molde, tiempo de inyección, tiempo de enfriamiento y tiempo de expulsión de la pieza. Por otra parte, es importante mencionar que cada polímero presenta una región óptima recomendada para su transformación, la cual es denominada rango o ventana de procesabilidad y está determinada por valores extremos de temperatura y presión. Bajos valores de presión provocarán que la pieza no alcance su peso óptimo, a la vez de que el porcentaje de contracción sea muy alto, mientras que con altos valores de presión de inyección, se obtendrán piezas con rebabas y concentraciones internas de esfuerzos. Estas rebabas son originadas cuando la presión en la cavidad supera a la fuerza de cierre, por lo que entonces material puede fluir a través del plano de partición del molde. En el caso de la temperatura, bajos valores provocarán la obtención de piezas incompletas o de un gran aumento del tiempo de ciclo, mientras que si la temperatura del fundido es muy alta, el material va a sufrir de degradación térmica [2-3] . En la figura 3.2 es posible observar un ejemplo de ventana de procesamiento para polímeros. Figura 3.2 Ventana de procesabilidad para polímeros [10]. 8 3.2 PROPIEDADES MECÁNICAS El conocimiento y estudio de las propiedades mecánicas de los materiales, en general, constituye una herramienta fundamental en lo que se refiere al comportamiento de estos bajo distintas condiciones, a la vez de que proporciona restricciones en cuanto a su aplicación y uso final, las cuales son tomadas en consideración por los diseñadores de piezas. El estudio de las propiedades mecánicas se encuentra referido a la respuesta que presenta un cuerpo cuando se le somete a una fuerza externa, la cual genera relaciones del tipo tensorial con la deformación que sufre el material en cuestión. El análisis de las propiedades mecánicas es posible a través de diversas técnicas de ensayo, dependiendo en cada caso la propiedad que se desee evaluar, entre los tipos de ensayos más utilizados se pueden encontrar: tracción o tensión, compresión, fatiga, dureza e impacto. De los diferentes ensayos mencionados anteriormente, el más empleado es el ensayo de tensión uniaxial (en una sola dirección), el cual entrega la mayoría de los datos relevantes para un primer estudio mecánico de materiales. Este ensayo consiste principalmente en someter al material, el cual ha sido modelado con anterioridad en forma de una probeta normalizada, a una velocidad de deformación constante, y a continuación medir la fuerza necesaria para cada deformación, esto se realiza generalmente hasta que el material se fractura [11] . En la figura 3.3 se puede observar una representación esquemática del equipo utilizado para llevar a cabo el ensayo de tracción. Figura 3.3 Máquina para ensayos de tracción [12]. A partir de los datos obtenidos una vez realizado el ensayo de tracción, es posible calcular diversos valores del esfuerzo y la correspondiente deformación unitaria en el espécimen y luego graficar los resultados. La curva resultante es conocida como diagrama 9 esfuerzo-deformación y ésta es una característica del material particular que se está probando, a la vez de que también contiene información importante sobre las propiedades mecánicas y tipo de comportamiento [13-14]. En lo que se refiere al esfuerzo nominal o de ingeniería, éste es posible calcularlo dividiendo la carga P que está siendo aplicada entre el área Ao de la sección transversal original del espécimen. Este cálculo supone que el esfuerzo es constante en la sección transversal y está determinado por la siguiente ecuación: Esfuerzo = σ = P Ao ecuación 3.1 Así mismo, la deformación nominal o de ingeniería puede ser determinada al leer el calibrador o dividiendo el cambio en la longitud calibrada (δ), entre la longitud calibrada del espécimen Lo. Esto es representado a través de la siguiente expresión: Deformación = ε = δ Lo ecuación 3.2 En la figura 3.4 anteriormente mostrada, son presentados ejemplos de distintos tipos de curvas esfuerzo-deformación que pueden ser obtenidos dependiendo del material que sea Fuerza ensayado. Desplazamiento Figura 3.4 Curcas típicas para ensayos de esfuerzo-deformación: (a) Fractura frágil, (b) Fractura dúctil, (c) Formación de un cuello (punto de fluencia) y (d) Elastómeros [11]. De igual forma, a partir de estas curvas, es posible determinar entonces diferentes tipos de comportamiento así como etapas durante el proceso de deformación (dependientes del tipo de material ensayado), entre lo que se puede resaltar [11, 13-14]: 10 • Comportamiento Elástico: la curva es en realidad una línea recta en toda esta región, por lo que entonces el esfuerzo es proporcional a la deformación. Durante esta etapa el material regresa a su longitud original una vez retirada la carga. En general, en esta zona es posible aplicar la siguiente relación (análoga a la Ley de Hooke): σ = E *ε ecuación 3.3 en donde E corresponde al Módulo de Elasticidad o de Young, el cual es la constante que relaciona, en la zona elástica-lineal, la tensión con la deformación. • Fluencia: al sobrepasar el límite elástico de esfuerzo ocurre un proceso de deformación plástica, por lo que el material no será capaz de recuperarse completamente una vez retirada la carga. Primeramente, se puede observar un punto superior de fluencia, seguido de una disminución de la capacidad para soportar cargas hasta un punto inferior de fluencia luego del cual la pieza continúa deformándose sin un incremento considerable del esfuerzo requerido. • Endurecimiento por Deformación: durante esta etapa el material sufre cambios en su estructura cristalina (no ocurre en polímeros amorfos), de manera tal que es posible obtener una mayor resistencia a deformaciones adicionales. La carga finalmente alcanza su máximo valor (esfuerzo último). • Formación de cuello o Estricción: en el esfuerzo último, ocurre una disminución del área de la sección transversal en una sección localizada de la probeta. En vista de que el área está decreciendo continuamente la probeta solo será capaz de soportar cargas cada vez menores, por lo que entonces el diagrama esfuerzo-deformación tiende a curvarse hacia abajo hasta alcanzar el esfuerzo de fractura del material (σf). Este comportamiento es originado por planos de deslizamiento formados dentro del material. 11 3.3 CONCENTRADORES DE ESFUERZOS Cuando una carga axial es aplicada sobre una pieza, una complicada distribución de esfuerzos es generada alrededor de la zona o punto de aplicación de la fuerza. Si la sección transversal de ésta es uniforme y no se presenta ningún cambio abrupto, las ecuaciones de esfuerzos (ecuación 3.1) solo proporcionan los resultados para un esfuerzo promedio a lo largo de toda la sección transversal, no obstante, si existen discontinuidades en la pieza, el esfuerzo máximo en esta sección será considerablemente mayor que el esfuerzo promedio establecido en las ecuaciones anteriormente mencionadas. Estas posibles discontinuidades presentes en las piezas son conocidas como concentradores de esfuerzos y los altos esfuerzos generados por éstas, concentraciones de esfuerzos [13-15]. De lo anteriormente mencionado, la concentración de esfuerzos puede definirse entonces como una condición bajo la cual altos esfuerzos en zonas localizadas, son producidos como resultado de la geometría o forma de la pieza (irregularidades inherentes a ésta) [16-17]. Estas concentraciones de esfuerzos, por lo general, son expresadas en términos del factor Kt. Generalmente, el factor Kt se encuentra definido como la relación existente entre el esfuerzo máximo que determina el límite de proporcionalidad del material con el cual se elaboró la pieza (fluencia o ruptura) y el esfuerzo nominal basado en la sección transversal de la pieza. A continuación en la ecuación 3.4 se presenta el factor Kt para cargas de tracción y flexión, mientras que en la ecuación 3.5 es encontrado el Kt para cargas de torsión: Kt = σ max σ nom ecuación 3.4 Kt = τ max τ nom ecuación 3.5 El subíndice t presente en este factor indica que Kt siempre es una magnitud teórica, por lo que el factor experimental Kf (factor de concentración de esfuerzos experimental) será generalmente más bajo que Kt. De igual forma, es importante señalar que la magnitud de la concentración de esfuerzos depende de cuán abrupto sea el cambio de sección en la pieza [16, 18-21] . 12 Seguidamente en la figura 3.5 son presentados distintos ejemplos de concentradores de esfuerzos originados por ángulos afilados, cuñeros, elementos redondeados, agujeros y otros tipos de discontinuidades presentes en placas [22]: (a) (b) (c) (d) (e) (f) Figura 3.5 Tipos de concentradores de esfuerzos: (a) entalla triangular o tipo cuña, (b) entalla semicircular, (c) entalla rectangular, (d) cambio de sección o tipo hombro, (e) entalla semicircular que finaliza con lados rectos y (f) agujero [15-23]. Estos cambios en la geometría pueden provocar un estado tridimensional de esfuerzos en la pieza, por lo que la formación y propagación de las grietas será más crítica. Así mismo, es importante tener en consideración el tipo de material con el que se está trabajando, debido a que si es un material frágil el límite de proporcionalidad se encuentra en el esfuerzo de ruptura, provocando esto que al alcanzar este esfuerzo comience la formación de la primera grieta y en consecuencia se desarrolle una fuerte concentración de esfuerzo en su punta, lo cual simultáneamente conduce a la propagación de ésta y a la subsiguiente fractura súbita. Por este motivo es recomendable el empleo del factor Kt para el diseño de piezas con materiales frágiles. Por otra parte, cuando se trata de un material dúctil el límite de proporcionalidad se encuentra en la zona de fluencia, por lo que una vez alcanzado este valor no es probable que la pieza fracture, sin embargo, si existe la posibilidad de que pueda ocurrir una fractura frágil para este material el factor Kt debe ser tomado en consideración. Los factores Kt, por lo general, son reportados en forma de gráficas y es posible encontrarlos en manuales de ingeniería relacionados con el análisis de esfuerzos. En la figura 3.6 es posible observar algunas curvas de Kt para diferentes tipos de concentradores de esfuerzos [13, 23-24]: 13 Figura 3.6 Gráficas con los respectivos valores de Kt para barra rectangular metálica con diferentes concentradores de esfuerzos: (a) tipo hombro, (b) entalla en forma de “U” y (c) agujero [15]. En el pasado, el cálculo de estos factores solo había sido posible de realizar para casos simples, esto debido a las complejas dificultades matemáticas que implica, no obstante, en la actualidad es posible aplicar procedimientos de aproximación numérica, elementos finitos o ecuaciones diferenciales finitas con lo que problemas más complejos han sido posibles de calcular [24]. 14 3.4 HERRAMIENTAS DE DISEÑO Y SIMULACIÓN DE PROCESOS EN PIEZAS PLÁSTICAS El proceso de diseño ingenieril tiene como principal justificación, la concepción de ideas destinadas a la consiguiente solución de problemas tecnológicos, para lo cual se requiere el empleo de diferentes recursos, conocimientos y material ya existente. El diseño de un producto o de cualquier pieza plástica es un proceso de gran complejidad, en el cual la persona encargada de realizar el diseño debe conocer a cabalidad no solo aquellos aspectos relacionados a las condiciones finales y operativas del producto, sino también estar al tanto de las particularidades de los materiales con los que trabaja, además de todos aquellos factores que de una u otra forma ejercen influencia sobre la pieza durante su proceso de transformación [25-27]. Con la finalidad de llevar a cabo y facilitar la operación de todas las etapas del diseño, se han desarrollado nuevas tecnologías y programas computarizados. No obstante, hasta hace pocos años atrás el principal inconveniente para la utilización de estas herramientas era la necesidad de invertir grandes cantidades de dinero en complejos equipos informáticos, sin embargo, actualmente se ha hecho posible la generalización de estos software debido al constante crecimiento de la industria informática. Esta serie de programas permite que se pueda trabajar simultáneamente en todas las etapas del proceso de diseño, a la vez de que ofrecen una gran facilidad y versatilidad para la resolución de problemas complejos con una muy buena precisión. Es importante destacar que la gran mayoría de estos paquetes de software están basados en herramientas de discretización por métodos finitos, sumado a que es posible su aplicación a todo tipo de materiales. Además, en lo que se refiere a la industria plástica, existen programas particulares que pueden simular el proceso de inyección, el cual es el proceso de transformación empleado en este trabajo [26-28]. Entre las distintas formas de discretización existentes, el método de diferencias finitas (MDF) es el más simple de todos. Éste consiste en una aproximación de derivadas parciales por expresiones algebraicas, envolviendo los valores de la variable dependiente en un limitado número de puntos seleccionados. Como resultado de la aproximación, las ecuaciones diferenciales parciales que describen el problema son reemplazadas por un número finito de 15 ecuaciones algebraicas, escritas en términos de los valores de la variable dependiente en los puntos seleccionados. Sin embargo, es necesario tener en consideración que la discretización de ecuaciones diferenciales por métodos de diferencia finita presenta una serie de desventajas, entre las cuales se encuentran: la dificultad de satisfacer a plenitud las condiciones de borde y que la precisión de los resultados es pobre si no se trabaja con un número de elementos considerable [29-31]. Debido a esto, el método de elementos finitos (MEF) es la herramienta dominante en esta área debido a la gran flexibilidad que ofrece al estudio de piezas con geometrías complicadas, las cuales son las que comúnmente son encontradas en los productos elaborados por moldeo por inyección [32-35] . Este método, particularmente es usado para la resolución de ecuaciones diferenciales y sus respectivas condiciones de borde sobre una superficie de forma compleja. El dominio en cuestión es definido por un gran número de elementos finitos, los cuales a su vez se encuentran descritos por diferentes nodos. En la figura 3.7 es posible observar una representación de elementos finitos formando un dominio particular [36]. (a) (b) Figura 3.7 Métodos numéricos para la representación de un dominio: (a) MEF y (b) MDF [26-29]. Las herramientas computacionales desarrolladas y mencionadas anteriormente, se encuentran en la actualidad en una etapa de madurez, por lo que han abierto grandes posibilidades para el rediseño de piezas a la vez de que han contribuido a que los procedimientos de fabricación cambien radicalmente. Estas tecnologías pueden ser divididas en tres grandes grupos: Diseño Asistido por Computadora (CAD), Ingeniería Asistida por 16 Computadora (CAE) y Manufactura Asistida por Computadora (CAM), sin embargo es importante tener en cuenta que estos sistemas deben trabajar sinergísticamente para que los resultados sean los más óptimos. Seguidamente se presenta una descripción más detallada de cada uno de estos sistemas [37-39]: • Diseño Asistido por Computadora: permite la creación y diseño de la pieza o concepto principal a través de la computadora, haciendo posible el análisis y verificación del mismo. A su vez, es capaz de llevar a cabo distintas funciones, entre las que se pueden mencionar: − Base de datos de propiedades: diferente información a cerca de materiales, tolerancias, tratamientos térmicos, terminaciones superficiales. − Modelado geométrico tridimensional: a través de una descripción analítica del volumen, contorno y dimensiones del sistema, que incluye relaciones algebraicas y geométricas entre los distintos componentes. − Proyecciones bidimensionales del objeto o sistema: generación de planos con todo tipo de vistas, detalles, secciones y perspectivas posibles. • Ingeniería Asistida por Computadora: por medio de estos es posible realizar las simulaciones que reflejan el comportamiento del sistema en la realidad, así como su respectiva representación en la memoria del computador. Entre algunas de las principales aplicaciones CAE se encuentran: − Cálculo de propiedades físicas: masa, volumen, centro de gravedad, momentos de inercia, entre otros. − Análisis tensional y cálculo mecánico y estructural (lineal y no lineal). − Análisis de vibraciones. − Simulación del proceso de inyección de un molde: análisis dinámico y térmico del material inyectado (inyección virtual). − Simulación de procesos de fabricación: mecanizado, conformado de chapas metálicas, soldaduras, análisis de fijaciones (fabricación virtual). • Manufactura Asistida por Computadora: la principal función de esta herramienta es la búsqueda de la automatización en el proceso de manufactura de la pieza o producto que se desee realizar, esto a través de la traducción de las especificaciones de diseño a 17 especificaciones de producción. Entre las posibilidades de aplicación de los sistemas CAM se tiene: − Generación de programas de Control Numérico (CN). − Programación de soldaduras y ensamblajes robotizados. − Simulación de estrategias y trayectorias para el mecanizado del producto diseñado (partiendo de un modelo CAD), una vez establecidos todos los parámetros y variables necesarias. − Inspección asistida por computadora. − Ensayo asistido por computadora. Entre los principales beneficios que se pueden obtener al aplicar este tipo de tecnologías se encuentran, una mejora y aumento de la productividad, un mantenimiento del control de calidad más eficiente, mejor utilización de los recursos disponibles, progreso continuo en el desarrollo y perfección de piezas moldeadas. No obstante y a pesar de lo anteriormente expuestos, muchos empresarios mantienen la idea de que la adquisición de estos paquetes de software es un gasto innecesario, sin embargo, cada día el mercado de sistemas asistidos por computadora se posiciona más firmemente debido a la gran variedad de beneficios que ofrece [40]. En la figura 3.8 anteriormente presentada, se puede observar un esquema representativo del proceso de diseño y fabricación de un producto, con la respectiva aplicación de los sistemas CAD/CAE/CAM. 18 Figura 3.8 Ciclo de diseño y fabricación de un producto mediante la utilización de herramientas CAD/CAE/CAM [41]. Un par de herramientas que son muy representativas de estos programas de diseño y simulación corresponden a: A. PRO-ENGINEER: es descrito principalmente como un software de diseño tridimensional, no obstante éste posee distintos módulos, cada uno de los cuales puede desempeñarse en diferentes funciones CAD/CAE/CAM. De aquí que este sea una de las herramientas pilares al momento de desarrollar un producto mediante esta vía [42-43]. Entre las principales ventajas que presenta la utilización de este software, se encuentran: • Ser totalmente asociativo. Cualquier cambio que se realice en el diseño, inmediatamente es reflejado en todos los elementos subsecuentes. • Las aplicaciones totalmente integradas permiten desarrollar todo el proceso, desde el diseño inicial hasta la producción de la pieza. • Las prestaciones de creación de geometría proporcionan una diferenciación y fabricación superior de los productos. • El módulo de simulación permite mejoras en el rendimiento de los productos, así como la superación de los objetivos de calidad de los mismos. 19 • Dependiendo del módulo empleado se tiene a disposición información referente a herramientas de mecanizado, fresado, diseño de herramientas, control numérico, comportamiento de materiales, entre otros. B. C-MOLD: este corresponde a un sistema integrado CAE destinado al estudio del proceso de inyección de plásticos. Así mismo, este es capaz de proveer información sustancial y muy completa de todas las etapas correspondientes a diseño y manufactura del producto, a la vez de que puede establecer los lineamientos para la mejora de la productividad y calidad de la pieza. Este sistema CAE puede ser empleado para resolver problemas concernientes tanto al molde de inyección, como a las distintas variables que corresponden a este proceso de transformación de plásticos (tiempo de llenado, presión de inyección, contracción, alabeo, eficiencia del refrigerante, posición óptima de la entrada, temperatura de desmoldeo). De igual forma, es capaz de analizar y generar resultados para otros procesos de transformación e inyección no tradicional, entre los cuales se encuentran la co-inyección, el moldeo por inyección/compresión, el termoformado, el moldeo reactivo, etc. Otras características presentes en C-MOLD incluyen una interfaz gráfica con un fácil acceso a la visualización de resultados, un modelador para distintas geometrías, capacidad de integración con la mayoría de los sistemas CAD y CAE estructurales y capacidad de mallado mediante el empleo de elementos finitos [44-45]. Con respecto a esto último, se hace importante resaltar que en un estudio realizado por Candal y colaboradores [46], se observó que los valores obtenidos a partir de mallas realizadas en un programa modelador son más parecidos a los resultados experimentales, debido a que esta malla copia mejor los detalles de la pieza, además de que presenta la capacidad de modificar el tamaño y posición de los elementos empleados, mientras que con mallas CAE solamente el número de elementos puede ser variado, por lo que la distribución de estos es exactamente la misma a lo largo de todo el espécimen de estudio. 20 3.5 ANTECEDENTES La concentración de esfuerzos es un aspecto de vital importancia para el estudio de piezas metálicas o plásticas, debido a que de esto dependerán sus propiedades mecánicas y por lo tanto las aplicaciones finales a las que sean sometidas. Por su parte, González [22] evaluó la influencia que presenta la adición de múltiples concentradores de esfuerzos sobre el factor Kt. De esto se consiguió que la adición de agujeros colocados en distintas posiciones de una placa, de diferentes tamaños y distancias a partir del agujero central, permitiera aumentar el rendimiento de una pieza. De igual forma, los resultados fueron obtenidos a través de dos métodos, en donde el primero estuvo basado en la interpretación de tablas y gráficos disponibles en la literatura para materiales metálicos, como los publicados por Peterson [47] , mientras que el segundo se basó en el análisis matemático y la aplicación de herramientas computacionales. Estudios relacionados a la concentración de esfuerzos en piezas plásticas han sido llevados a cabo, tal es el caso de la investigación realizada por Candal y colaboradores [48], en donde se evaluó la concentración de esfuerzos en piezas moldeadas por inyección de un estuche para CD a través de herramientas computacionales y utilizando como materiales principales Poliestireno cristal (PS) y Poliestireno de Alto Impacto (PSAI). A partir de este trabajo fue posible determinar tres constantes para cada material, definidas como: (a) una constante cuyo esfuerzo nominal fue obtenido a través de simulaciones para condiciones de servicio (K1 servicio), (b) una constante relacionada a los esfuerzos tanto en el procesamiento como en condiciones de servicio (K1 procesamiento), y finalmente, (c) una constante cuyo esfuerzo nominal es establecido por medio de un programa modelador bajo condiciones de servicio (K2 servicio). De aquí se pudo obtener que la simulación de esfuerzos en cargas de servicio no toma en consideración los esfuerzos durante el procesamiento, ni la orientación inducida en la pieza, de manera que la distribución de esfuerzos es diferente a la real. Por otra parte, Jiménez [49] y Candal y colaboradores [7, 50-51] estudian el efecto de concentradores de esfuerzos triangulares sobre las propiedades mecánicas de piezas plásticas. De esta investigación se obtuvo que los resultados de esfuerzos y del factor Kt resultantes a través de simulación y experimentalmente se encontraron bastante cercanos, por lo que se establece la validez del método de simulación. Así mismo, bajo las condiciones de inyección empleadas, a medida de que la profundidad de la entalla disminuye, el factor Kt se 21 incrementa. En este trabajo, igualmente se estudió el efecto de las condiciones de operación sobre el factor Kt, de lo cual se obtuvo que este factor se incrementa con la presión de inyección hasta alcanzar un valor constante, mientras que con incrementos sucesivos de la presión sostenida el Kt disminuye. Otros estudios referentes a la concentración de esfuerzos en piezas plásticas bajo la influencia de concentradores de esfuerzos, están basados principalmente en el efecto que presentan las líneas de soldadura generadas por el encuentro de dos frentes de flujo sobre las propiedades mecánicas finales. La investigación realizada por Spoormaker y Heidweiller [52] demuestra que la capacidad para soportar cargas en una pieza con un concentrador de esfuerzo tipo circular, va a depender fuertemente de la temperatura del material fundido que es inyectado en el molde. Cuando la temperatura del fundido es baja, las moléculas cercanas a las paredes se van a encontrar sumamente orientadas y el tiempo de relajación será corto, mientras que cuando la temperatura es alta, las moléculas cercanas a las paredes serán menos orientadas y tendrán un tiempo más amplio para relajarse. En este caso, la fuerza de las piezas será inferior, pero la fuerza de la línea de soldadura aumentará. Sumado a esto, Heidweiller y Van Der Zwet [53] también realizaron estudios sobre piezas con agujeros en su interior, de donde concluyeron que en la medida de que el diámetro del agujero sea más grande, aumentará el área de concentración de esfuerzos. Igualmente obtuvieron que la línea de soldadura formada es el punto más débil de la pieza, no obstante, la reducción en la capacidad para soportar cargas es pequeña si se compara con la orientación inducida sobre el material. Finalmente esta investigación arrojó que las condiciones de operación no afectan directamente. Por último, en cuanto al establecimiento y desarrollo de ecuaciones constitutivas, es posible encontrar algunos modelos tanto para metales como para plásticos, entre los cuales vale la pena mencionar los modelos de Johnson-Cook, G´Sell-Jonas, Matsuoka y Brooks. Cada uno de estos modelos, presentan de una manera u otra diversas relaciones para el esfuerzo o esfuerzos generados sobre una pieza determinada con respecto a variables del proceso de manufactura, entre las cuales es posible encontrar velocidades de deformación, temperaturas, tiempos y constantes de cada material en particular [54-57] . De igual manera, otros trabajos que demuestran la influencia de las condiciones de operación sobre las propiedades mecánicas de los materiales han sido realizados. Tal es el caso de la investigación 22 llevada a cabo por Trejo y Villablanca [58], en donde se señala que el módulo elástico a flexión (Eb) y el esfuerzo máximo a la fluencia a flexión (σfm) presentan una ligera disminución al incrementarse la temperatura del fundido, atribuido esto a una menor orientación y tamaño de la piel, mientras que el comportamiento a impacto es fuertemente influenciado por los fenómenos de orientación y relajación de esfuerzos, observándose que la presión sostenida y la temperatura del fundido son los factores más influyentes en la ventana de proceso. 3.6 JUSTIFICACIÓN DEL PROYECTO Con el paso de los años, el diseño de piezas plásticas ha ido evolucionando e innovando fuertemente, esto debido a la inclusión de nuevas variables y tecnologías dispuestas para este propósito. No obstante, aún en nuestros días los diseñadores continúan utilizando parámetros que corresponden a materiales diferentes a los plásticos, en donde los más estudiados han sido los metales. Un parámetro que representa gran importancia al momento de diseñar cualquier pieza, corresponde al factor Kt, para el cual existe en la literatura toda una serie de ecuaciones y gráficos a los cuales se puede recurrir dependiendo del tipo de metal a emplear, sin embargo, se hace necesario señalar que para materiales plásticos no se han realizado ninguno de estos cálculos. Es por esto que este trabajo está orientado principalmente a estudiar y elaborar una serie de gráficas para este factor Kt, variando tanto la geometría de los diferentes concentradores, así como las condiciones de operación mediante el empleo de herramientas CAD/CAE, con la finalidad de que los diseños de piezas elaboradas de alguna resina plástica puedan ser cada vez más precisos y ajustados a la realidad. De igual manera, se pretende sentar un precedente en cuánto al cálculo y utilización de herramientas y variables de diseño, así como para la determinación de todas aquellas variables que puedan o no influir en estos parámetros. De esta manera, los diseñadores de piezas plásticas podrán tener consciencia de la importancia que esto tiene para la obtención de resultados cada vez más óptimos. CAPÍTULO IV METODOLOGÍA Con la finalidad de desarrollar todos los objetivos propuestos para este proyecto, se llevaron a cabo diferentes etapas las cuales constituyen la metodología empleada. Para la realización de este trabajo se tomó en consideración la metodología establecida por Jiménez [49] y Candal y colaboradores [7] , a partir de la cual fue posible seguir las siguientes fases: • Revisión bibliográfica. • Diseño y mallado preliminar de las placas en el programa modelador Pro-ENGINEER. • Montaje de los sistemas en C-MOLD. • Determinación del número de nodos óptimo mediante el empleo del criterio de la convergencia. • Simulación del proceso de inyección y del ensayo de tracción, para diferentes geometrías de entallas y variación en las condiciones de operación en C-MOLD. • Determinación del parámetro de concentración de esfuerzos (Kt). Por último, se llevó a cabo la determinación de ecuaciones constitutivas, con la finalidad de establecer un modelo matemático para la obtención del factor Kt en piezas plásticas. 4.1 REVISIÓN BIBLIOGRÁFICA Inicialmente se realizó un exhaustivo sondeo de las posibles fuentes de información disponibles, así como del contenido a investigar, sin embargo, es importante señalar que la gran cantidad de trabajos realizados en el área de concentración de esfuerzos, han sido desarrollados para materiales metálicos, por lo que el encontrar bibliografía especializada para plásticos se hizo una labor cuesta arriba, ya que existen contados trabajos que abarcan estos tópicos. No obstante, partiendo de los estudios en materiales metálicos, se mantiene un precedente por lo que es posible tener nociones a cerca de los potenciales comportamientos que puedan ser encontrados en piezas plásticas. 24 Así mismo, se recopiló toda la información requerida en cuanto a las propiedades mecánicas de los materiales, utilización de herramientas CAD/CAE, proceso de inyección, sus variables y cómo estas afectan las propiedades de las piezas inyectadas. Esta información sí fue de fácil accesibilidad a través de libros especializados, revistas electrónicas e impresas, papers, congresos, entre otras vías encontradas en las bibliotecas de la Universidad Simón Bolívar y el IVIC, además de internet. 4.2 DISEÑO Y MALLADO PRELIMINAR DE LAS PLACAS EN EL PROGRAMA MODELADOR Pro-ENGINEER Primeramente, se establecieron los tipos de concentradores de esfuerzos a trabajar, esto partiendo de la información disponible en la literatura y más específicamente en los concentradores presentados en la figura 3.5. De esta serie de concentradores de esfuerzos, finalmente se acordó emplear los del tipo circular, semicircular, triangular y rectangular. Una vez establecido esto, se procedió al diseño mediante el programa modelador ProENGINEER de todas las placas requeridas con sus respectivas entallas. Cuatro dimensiones principales fueron mantenidas presentes en cada una de las placas, esto de acuerdo a lo establecido en la bibliografía para barras rectangulares metálicas entalladas. Estas dimensiones corresponden a lo siguiente [15]: D= Ancho total de la placa h= Altura de la entalla d= Relación D-2h r= Ancho de la entalla A continuación en la figura 4.1 son presentadas las distintas placas diseñadas con sus respectivos concentradores de esfuerzos y dimensiones principales. Adicionalmente, en el Apéndice A es posible observar los planos realizados en Pro-ENGINEER para cada una de las placas evaluadas. 25 r r h d h D (a) D d (b) r h d/2 D d D d/2 (c) (d) Figura 4.1 Placas diseñadas en Pro-ENGINEER con sus dimensiones principales: (a) Triangular, (b) Rectangular, (c) Circular y (d) Semicircular. Seguidamente en las tablas 4.1 y 4.2 es posible observar las diferentes dimensiones de concentradores utilizadas. De igual manera, es importante mencionar que durante la evaluación de cada una de estas condiciones los parámetros de operación del proceso de inyección fueron mantenidos constantes en las siguientes magnitudes: temperatura del fundido (230 °C), presión sostenida (7 MPa), velocidad de inyección (5,5 cm/s) y temperatura del refrigerante (35 °C). Tabla 4.1 Dimensiones empleadas para concentradores de esfuerzos triangular y rectangular. Nº Entalla 1 2 3 4 5 6 7 8 9 10 11 12 13 Base (mm) 16 16 16 16 16 16 16 10 13 19 22 25 28 Altura (mm) 7 10 13 16 19 22 25 13 13 13 13 13 13 26 Tabla 4.2 Dimensiones empleadas para concentradores de esfuerzos circular y semicircular. Nº Entalla 1 2 3 4 5 6 7 8 Diámetro (mm) 7 10 13 16 19 22 25 28 Luego de diseñadas todas las placas, estas fueron malladas mediante la aplicación del módulo Pro-MECHANICA incluido en el sistema CAD empleado [49] . Seguidamente, en la figura 4.2 se presentan las distintas mallas creadas a través de la utilización de ProENGINEER. (a) (b) (c) (d) Figura 4.2 Mallas realizadas a placas con entallas: (a) Triangular, (b) Rectangular, (c) Circular y (d) Semicircular. 4.3 MONTAJE DE LOS SISTEMAS EN C-MOLD Se procedió al montaje del molde de las placas (unidad de inyección y sistema de refrigeración) bajo los parámetros establecidos por el software de simulación de polímeros 27 C-MOLD. Inicialmente se realizó un importe de la malla (.fem) al programa C-MOLD desde Pro-ENGINEER. En este punto, se comenzó con la construcción de todas las partes que corresponderían al molde, entre las cuales se encuentran las entradas, canales de alimentación, bebedero y canales de refrigeración, de igual forma las placas y demás partes fueron localizadas según lo descrito en los planos pertenecientes a un molde preexistente (Apéndice A). No obstante, es necesario señalar que una de las placas tuvo que ser levemente desplazada de su posición original, debido a que la entrada a la cavidad coincidía con el lugar dispuesto para las entallas. Una vez concluido el montaje principal (Figuras 4.3 a 4.6), se procedió al establecimiento de todas las variables involucradas en el proceso de inyección y que pueden ser manipuladas en C-MOLD. Primeramente y a partir de la base de datos del software, se seleccionaron el tipo de resina, máquina de inyección y material de elaboración de las placas del molde a utilizar, mientras que en una segunda etapa, fue posible la manipulación de parámetros de inyección como la presión sostenida, velocidad de inyección, temperatura del fundido y temperatura del líquido refrigerante. De igual manera, se verificaron variables como la temperatura de las placas del molde y el esfuerzo máximo permisible, con la finalidad de que se encontraran dentro de los rangos establecidos para la resina seleccionada. Figura 4.3 Sistema empleado para las simulaciones correspondientes a la placa con entalla triangular en C-MOLD. 28 Figura 4.4 Sistema empleado para las simulaciones correspondientes a la placa con entalla rectangular en C-MOLD. Figura 4.5 Sistema empleado para las simulaciones correspondientes a la placa con entalla circular en C-MOLD. Figura 4.6 Sistema empleado para las simulaciones correspondientes a la placa con entalla semicircular en C-MOLD. 29 Por otro lado, es importante mencionar el especial cuidado que se tuvo con el establecimiento y asignación de las fuerzas y restricciones necesarias para la simulación del ensayo de tracción. Para llevar a cabo esto, primeramente fueron colocados los nodos de la parte más externa de las placas de manera equidistante, de tal forma que la fuerza pudiese ser distribuida igualmente. Una vez logrado esto, se le asignó a cada nodo un punto de fuerza en la dirección a estudiar en el ensayo tensil. Seguidamente, la magnitud del esfuerzo de fluencia propio del material y disponible en la base de datos de C-MOLD fue multiplicada por el área transversal de la placa en la zona de la entalla, esto con la finalidad de obtener la fuerza máxima a aplicar (Fmáx), y posteriormente fue dividida entre n-1 nodos, en donde n corresponde al total de nodos dispuestos sobre el borde de la placa. En la figura 4.7 se puede apreciar la localización de las fuerzas en el extremo de una placa, en donde la magnitud de la fuerza asignada para los nodos N2 al N6 es igual a Fmáx/(n1) y para los nodos N1 y N7 es igual a Fmáx/2(n-1), esto último por estar los nodos dispuestos en las esquinas, con lo que el radio de acción de la fuerza sobre la placa es equivalente a la mitad del de los nodos interiores. N1 N2 N3 N4 N5 N6 N7 Figura 4.7 Fuerza nodal establecida en una de las placas estudiadas. De igual forma, fue necesaria la colocación de restricciones en todas las direcciones (de desplazamiento y rotacionales), con el objetivo de simular el efecto de las mordazas que sostienen a una muestra en una máquina de ensayos universales. En la figura 4.8 es posible observar un detalle de estas restricciones sobre una placa con entalla semicircular. 30 Figura 4.8 Restricciones establecidas en una de las placas estudiadas. 4.4 DETERMINACIÓN DEL NÚMERO DE NODOS ÓPTIMO MEDIANTE EL EMPLEO DEL CRITERIO DE LA CONVERGENCIA A través de la puesta en práctica de un criterio de convergencia, se pretende principalmente obtener resultados más precisos y ajustados a la realidad [59]. Para el desarrollo de este criterio, se seleccionó en cada forma de concentrador la geometría más pequeña, debido a que ésta debería corresponder a la más crítica en cada caso. A partir de esto, se realizaron mallados de las placas en cuestión con diferente número de nodos, en donde las magnitudes empleadas fueron 10, 20, 30, 40, 50, 60, 70 y 80 nodos. Esta variación en el número de nodos fue llevada a cabo únicamente en las secciones correspondientes a las entallas, debido a que es en los alrededores a estas zonas en donde los cambios de flujo se suponen serán más importantes, y por lo tanto, en donde se requiere que el estudio sea más exacto. Este procedimiento se efectuó nuevamente bajo lo establecido por Jiménez [49] en su metodología. De los resultados reportados por C-MOLD, los que se tuvieron en consideración para evaluar este criterio fueron los de tiempo de llenado, tiempo de ciclo, esfuerzo de corte en la pared del molde antes del tiempo de llenado y esfuerzo promedio en cargas de servicio. Esto debido a que se conocía con antelación la efectiva convergencia de estos resultados, de acuerdo a estudios realizados por Candal y colaboradores [46] , sin embargo, otros resultados fueron estudiados y analizados también, con la finalidad de verificar si en realidad existen resultados adicionales que convergen de la misma manera, además de encontrar aquellos que 31 no convergen y cuáles convergen desde el principio. El número de nodos óptimo corresponde al punto de la gráfica variable vs. número de nodos, a partir del cual ya no existen variaciones significativas en los resultados. A continuación, en la figura 4.9 se presentan placas con distinto número de nodos, en donde es posible verificar las diferencias en la zona correspondiente a las entallas. (a) (b) (c) Figura 4.9 Placas con entalla circular y diferente número de nodos; (a) 10 nodos, (b) 40 nodos y (c) 80 nodos. 4.5 SIMULACIÓN DEL PROCESO DE INYECCIÓN Y DEL ENSAYO DE TRACCIÓN, PARA DIFERENTES GEOMETRÍAS DE ENTALLAS Y VARIACIÓN DE LAS CONDICIONES DE OPERACIÓN EN C-MOLD Con la finalidad de realizar las simulaciones pertinentes a este estudio, fue seleccionada una máquina de inyección genérica de 200 toneladas, un acero P-20 como material de fabricación del molde y agua como líquido refrigerante. Así mismo, la resina empleada correspondió a un PSAI PS 8720 de la casa comercial BASF, el cual se encuentra dentro de la base de datos suministrada por C-MOLD, por lo que de antemano se contaba con las constantes reológicas y curva P-v-T necesarias para llevar a cabo las simulaciones. En la tabla 4.3 son presentadas algunas de las características disponibles para este material. 32 Tabla 4.3 Propiedades de la resina empleada para las simulaciones en C-MOLD. Propiedades Módulo tensil Esfuerzo tensil a fluencia Máximo esfuerzo de corte Valor (MPa) 1850 22 0,24 La simulación del proceso de inyección fue realizada en una primera instancia para todas las formas de concentradores de esfuerzos a estudiar y sus respectivas geometrías, las cuales fueron presentadas en las tablas 4.1 y 4.2 de este trabajo. Con esto, se pretendió evaluar el efecto de la concentración de esfuerzos a nivel geométrico únicamente, manteniéndose entonces las condiciones de operación constantes en todos los casos. En una segunda etapa, se estudió la influencia de estos concentradores de esfuerzos sobre las propiedades de las placas a medida de que se variaban los parámetros de operación establecidos para el ciclo de inyección. Para llevar a cabo esto, fue mantenida constante una sola geometría para cada concentrador empleado. Esta selección fue basada en una serie de gráficas esfuerzo en cargas de servicio vs. posición en la placa, las cuales fueron elaboradas para cada una de las geometrías disponibles, en donde finalmente fue escogida aquella dimensión en la cual la variación de los resultados de estas curvas fue la mayor. Finalmente, el ensayo de tracción en las placas fue simulado simultáneamente en cada caso, y de este fue posible obtener los resultados correspondientes a esfuerzos en cargas de servicio y durante el procesamiento, requeridos para el estudio y cálculo del factor Kt. A continuación en la tabla 4.4 son presentados los parámetros de operación empleados para las condiciones evaluadas en las diferentes placas. Los valores mostrados en la primera fila, corresponden a las condiciones fijas usadas en las simulaciones con cambios en la geometría de las entallas. De igual manera, los tiempos de enfriamiento y de molde abierto, así como la temperatura de las placas del molde fueron mantenidos constantes para todos los casos simulados, teniendo como magnitudes 40 s, 3 s y 50 °C respectivamente. 33 Tabla 4.4 Condiciones de operación utilizadas para las distintas simulaciones realizadas. Tfundido (°C) Psostenida (MPa) Vinyeccion (cm/s) Trefrigerante (°C) 230 7 5,5 35 230 5 5,5 35 230 6 5,5 35 230 7 5,5 35 230 8 5,5 35 230 9 5,5 35 190 7 5,5 35 210 7 5,5 35 230 7 5,5 35 250 7 5,5 35 270 7 5,5 35 230 7 4,5 35 230 7 5,5 35 230 7 6,5 35 230 7 7,5 35 230 7 8,5 35 230 7 5.5 25 230 7 5.5 35 230 7 5.5 48 4.6 DETERMINACIÓN DEL PARÁMETRO DE CONCENTRACIÓN DE ESFUERZOS Luego de obtenidos los valores resultantes de las distintas simulaciones para los ensayos tensiles, se procedió a la medición de los esfuerzos generados en la zona de las entallas y a través de las placas. Conforme a lo establecido en la literatura [14-21] , el factor Kt puede ser calculado de acuerdo a la siguiente ecuación: Kt = σ max σ nom ecuación 4.1 donde σmax corresponde al esfuerzo medido a través de la simulación, mientras que σnom equivale al esfuerzo nominal o teórico para el sistema estudiado. Para la obtención del factor Kt mediante el empleo de herramientas CAD/CAE, se hace necesario utilizar σmax como el esfuerzo de Mises-Hencky (en cargas de servicio y procesamiento) reportado por C-MOLD para una placa sin entalla, a la vez de que σnom como el esfuerzo de Mises-Hencky para las distintas placas con entallas. 34 Una vez calculados los valores correspondientes a Kt, tanto para variación de la geometría como para variación de las condiciones de operación, fueron graficadas una serie de curvas Kt vs. parámetro estudiado. A cada una de estas curvas se le realizó un ajuste del tipo polinómico de segundo grado en el programa Microsoft Excel, debido a que fue la de mejor concordancia en la mayoría de los casos. Así mismo, fueron obtenidas las ecuaciones características para cada curva. En la figura 4.10 es posible observar un detalle de los esfuerzos de Mises-Hencky medidos a través de la placa y en las áreas correspondientes a las entallas. σ 0 + Figura 4.10 Detalle de los valores de esfuerzo tomados en la zona de la entalla (Esfuerzo de MisesHencky para cargas de servicio). 4.7 DESARROLLO DE UNA METODOLOGÍA PARA LA REALIZACIÓN DE ECUACIONES CONSTITUTIVAS Para desarrollar estas ecuaciones, se partió del modelo establecido por G´Sell el cual está basado en expresiones que cumplen la ley de Norton-Hoff usualmente utilizada para metales [60-62] . El propósito fundamental para el desarrollo de este modelo, corresponde a la necesidad de obtener una herramienta confiable y eficaz a través de la cual pueda ser calculado el factor Kt en piezas plásticas, sin importar las condiciones bajo las cuales fue elaborada la pieza, así como la geometría y discontinuidades que presente. Así mismo, mediante este método se evita tener que realizar cualquier tipo de ensayo adicional, a la vez de que se facilita la manipulación de este factor al momento de diseñar cualquier pieza en particular. 35 La metodología a seguir para llevar a cabo este tipo de ecuaciones constitutivas corresponde a los pasos mostrados a continuación: • Revisión bibliográfica. • Elaboración de gráficas tipo Arrhenius para las temperaturas del fundido y del líquido refrigerante. • Obtención de las expresiones cuadráticas resultantes de cada una de las relaciones graficadas para el factor Kt, como función de las distintas condiciones evaluadas. • Desarrollo de expresiones cuadráticas e iteraciones, mediante el empleo del software ORIGIN. CAPÍTULO V DISCUSIÓN DE RESULTADOS 5.1 CRITERIO PARA LA CONVERGENCIA DE RESULTADOS EN SIMULACIONES REALIZADAS BAJO SISTEMAS CAE Como ha sido mencionado con anterioridad, el diseño y mallado de las distintas placas a trabajar fue realizado mediante la utilización del programa Pro-ENGINEER y más específicamente por medio de su módulo Pro-MECHANICA, el cual corresponde a una herramienta CAD o de diseño asistido por computadora. Esto fue realizado de esta manera, debido a que de acuerdo a estudios realizados por Candal y colaboradores [46], los resultados obtenidos en simulaciones con mallas efectuadas en programas modeladores se ajustan de una manera eficiente a los obtenidos experimentalmente, debido a que estas mallas copian mejor todos los detalles existentes en la pieza, a la vez de que presentan la posibilidad de modificar el tamaño y la posición de los elementos empleados, mientras que las mallas elaboradas a través de herramientas CAE únicamente permiten la variación del número de elementos, haciendo imposible un análisis exhaustivo y localizado de las zonas con cambios en su área transversal. De igual forma, los sistemas con mallas realizadas bajo programas modeladores exhiben una convergencia y tiempo de simulación más rápido que aquellos que han sido elaborados en algún software de simulación, como por ejemplo C-MOLD. El método de discretización de resultados empleado por este sistema corresponde al método de elementos finitos (MEF), esto debido a la generalidad sistemática que convierte a esta técnica en una herramienta muy poderosa y versátil para la solución de un amplio rango de problemas [23] . El MEF permite la colocación de una mayor cantidad de elementos alrededor de las zonas más críticas o intrincadas de la pieza, a diferencia del MDF para el cual es necesario la disposición de una mayor cantidad de elementos, lo que se ve fuertemente reflejado en el tiempo necesario para llevar a cabo la simulación. Sin embargo, si no se coloca la cantidad necesaria de elementos en este caso, entonces la simulación del proceso sobre la pieza no va a corresponderse con la realidad, a la vez de aumentará la dificultad para establecer propiedades en los elementos de borde [29-30]. 37 De igual manera, al llevar a cabo el mallado de la pieza en Pro-ENGINEER únicamente es posible seleccionar elementos cuadriliterales o triangulares, por lo que estos últimos fueron seleccionados debido a la capacidad de obtener el menor radio de aspecto posible, así como el mayor número de elementos por unidad de área. No obstante y a pesar de lo anteriormente descrito, en la actualidad existen plataformas computacionales más avanzadas y que permiten un control y manejo más eficiente del proceso de mallado mediante elementos finitos. Un evidente ejemplo de este caso corresponde al programa simulador Moldex3D, el cual a pesar de ser una herramienta CAE permite al usuario un eficiente modelamiento del mallado, a la vez de que rompe con la brecha que anteriormente existía entre los sistemas CAD y CAE. Así mismo, admite la creación y disposición de una mayor gama de geometrías para los elementos a colocar sin incrementar el tiempo de simulación, tales como hexagonales, prismáticos, triangulares, tetraédricos, e incluso ofrece la posibilidad de realizar un mallado híbrido, lo cual es lo más idóneo para piezas que presenten discontinuidades. Debido a estos beneficios y a muchos más, sería recomendable la adquisición y empleo de este tipo de software para futuras investigaciones [63]. La convergencia de resultados mediante el MEF, utilizando una configuración de refinamiento de la malla, es decir, incrementando el número de nodos o elementos se denomina convergencia-h, mientras que el tipo de convergencia basado en el aumento del grado polinómico se llama convergencia-p. De esto es necesario destacar que el método empleado durante este trabajo fue el de la convergencia-h, debido a que las distintas placas presentan cambios abruptos en su geometría por lo que fue necesario el suministrar una malla más densa alrededor de esas zonas, con la finalidad de conseguir resultados más precisos [64-66]. De todos los posibles resultados disponibles luego de las simulaciones, finalmente fueron tomados en consideración para el establecimiento del criterio de convergencia los referidos a tiempo de llenado de la pieza dentro del molde, tiempo de ciclo y esfuerzo de corte en la pared del molde antes del tiempo de llenado. Estos resultados en particular fueron seleccionados de acuerdo a un estudio previo elaborado por Candal y colaboradores [66] , a partir del cual se verifica la correcta convergencia de estos, así mismo, también se utilizó el resultado pertinente a esfuerzo promedio en cargas de servicio, debido a la gran relevancia 38 que presenta para el trabajo en cuestión y en donde se verificará más adelante que es el resultado que más tarda en converger. La figura 5.1 mostrada a continuación, corresponde a los gráficos de los resultados de la simulación empleados para el criterio de convergencia en función del número de nodos, para el caso de una entalla del tipo semicircular. Tiempo de llenado (s) 40 30 20 10 0 Esfuerzo de corte en la pared antes de t de llenado (MPa) 0 10 20 30 40 50 60 70 80 90 10 20 30 40 50 60 70 Nº de nodos en la entalla (a) (b) 0,2 0 10 0 Nº de nodos en la entalla 0,4 0 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 20 30 40 50 60 70 80 90 Esfuerzo promedio en cargas de servicio (MPa) Tiempo de ciclo (s) 50 Nº de nodos en la entalla (c) 80 90 80 90 80 40 0 0 10 20 30 40 50 60 70 Nº de nodos en la entalla (d) Figura 5.1 Resultados analizados para el criterio de convergencia de la entalla semicircular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. De aquí es posible observar que el primer resultado en converger es el de tiempo de llenado el cual lo hace para 20 nodos, seguidamente el resultado correspondiente al tiempo de ciclo alcanza el punto de convergencia en mallas a partir de 40 nodos, sin embargo tanto para el esfuerzo de corte en la pared del molde, como para el esfuerzo promedio en cargas de servicio es necesario que se cuente con al menos 50 nodos para que los valores puedan estabilizarse. Es por este motivo que finalmente para las simulaciones realizadas en placas con concentrador de esfuerzos de tipo semicircular, fue obligatorio el mallado de cada una de ellas con 50 nodos alrededor de la discontinuidad. El mismo procedimiento anterior fue seguido para las restantes geometrías de entallas estudiadas, para las cuales se obtuvo que el número de nodos óptimo para alcanzar la 39 convergencia en concentradores circulares fue de 40 nodos, mientras que para entallas rectangulares y triangulares el número de nodos fue de 70 en ambos casos. Al igual que para el caso del concentrador de esfuerzos semicircular, las gráficas correspondientes a estos últimos pueden ser observadas en las figuras 5.2 a 5.4 de este trabajo, haciéndose evidente 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 Tiempo de ciclo (s) Tiempo de llenado (s) que estas siguen exactamente las mismas tendencias explicadas para la primera entalla. 40 30 20 10 0 0 10 20 30 40 50 60 70 80 90 0 10 20 30 40 0,35 0,3 20 30 40 70 80 90 80 90 (b) 0,4 80 Esfuerzo promedio en cargas de servicio (MPa) Esfuerzo de corte en la pared antes de t de llenado (MPa) (a) 10 60 Nº de nodos en la entalla Nº de nodos en la entalla 0 50 50 60 70 80 40 0 0 90 10 20 30 40 50 60 70 Nº de nodos en la entalla Nº de nodos en la entalla (c) (d) 50 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 Tiempo de ciclo (s) Tiempo de llenado (s) Figura 5.2 Resultados analizados para el criterio de convergencia de la entalla circular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. 0 10 20 30 40 50 60 70 80 40 30 20 10 0 90 0 10 20 30 0,4 0,2 0 10 20 30 40 50 60 50 60 70 80 90 80 90 (b) Esfuerzo promedio en cargas de servicio (MPa) Esfuerzo de corte en la pared antes de t de llenado (MPa) (a) 0,6 0 40 Nº de nodos en la entalla Nº de nodos en la entalla 70 80 90 80 40 0 0 10 20 30 40 50 60 70 Nº de nodos en la entalla Nº de nodos en la entalla (c) (d) Figura 5.3 Resultados analizados para el criterio de convergencia de la entalla rectangular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. 50 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 Tiempo de ciclo (s) Tiempo de llenado (s) 40 40 30 20 10 0 0 10 20 30 40 50 60 70 80 0 90 10 20 0,6 0,4 0,2 0 10 20 30 40 50 60 70 50 60 70 80 90 80 90 (b) 0,8 0 40 Nº de nodos en la entalla (a) Esfuerzo promedio en cargas de servicio (MPa) Esfuerzo de corte en la pared antes de t de llenado (MPa) Nº de nodos en la entalla 30 80 90 Nº de nodos en la entalla (c) 120 80 40 0 0 10 20 30 40 50 60 70 Nº de nodos en la entalla (d) Figura 5.4 Resultados analizados para el criterio de convergencia de la entalla triangular: (a) Tiempo de llenado, (b) Tiempo de ciclo, (c) Esfuerzo de corte en la pared antes de t de llenado y (d) Esfuerzo promedio en cargas de servicio. Es importante señalar que se tuvo que mantener en consideración, el hecho de que al incrementarse el número de nodos en el mallado, igualmente se incrementa el tiempo necesario para llevar a cabo la simulación del proceso, tal como lo previera Villarroel y colaboradores [16] . Por ello, como anteriormente fue expresado se decidió realizar el estudio por convergencia-h, de manera que fuese posible la escogencia del número de elementos óptimo y con él realizar todas las simulaciones. Adicionalmente, fueron estudiados otros resultados disponibles en el C-MOLD para dos formas distintas de concentrador de esfuerzos (semicircular y triangular) con el objetivo analizar la presencia o no de convergencia y de este modo poder ampliar el espectro de posibles resultados a tomar en consideración al momento de aplicar esta metodología. En las tablas 5.1 y 5.2 mostradas a continuación, son presentados todos los resultados adicionales estudiados para entallas semicirculares y triangulares, así como una descripción en cada caso de la convergencia o no descrita y bajo qué cantidad de nodos es establecida en el caso de ser posible, esto último dentro del rango de 10 a 80 nodos evaluados en las 41 simulaciones realizadas. Sumado a esto, en las figuras 5.5 y 5.6 también son mostradas las gráficas elaboradas para el criterio de la convergencia en placas con entallas triangulares. Tabla 5.1 Resultados adicionales estudiados para el criterio de la convergencia, en un concentrador de esfuerzos de tipo semicircular. Resultado Convergencia N° de nodos óptimo Temperatura de desmoldeo (°C) Sí 20 Temperatura de la masa al final del llenado (°C) Sí 20 Fuerza de cierre (Ton) Sí 50 Temperatura del refrigerante (°C) Siempre Número de Reynolds Siempre Temperatura de la pared del molde (°C) Sí 20 Porcentaje total en peso (%) Sí 30 Presión al final del llenado (MPa) Sí 50 Porcentaje de rechupe (%) Sí 30 Diferencia de temperatura (°C) No Contracción volumétrica (%) Sí 30 Sí 50 Flujo de calor en la pared del molde (W/m2) Desplazamiento en dirección X (mm) Sí 60 Desplazamiento en dirección Y (mm) Sí 60 Desplazamiento en dirección Z (mm) No - Tabla 5.2 Resultados adicionales estudiados para el criterio de la convergencia, en un concentrador de esfuerzos de tipo triangular. Resultado Convergencia N° de nodos óptimo Temperatura de desmoldeo (°C) Sí 20 Temperatura de la masa al final del llenado (°C) Sí 40 Fuerza de cierre (Ton) No Temperatura del refrigerante (°C) Siempre Número de Reynolds Siempre Temperatura de la pared del molde (°C) Sí 30 Porcentaje total en peso (%) Siempre Presión al final del llenado (MPa) No Porcentaje de rechupe (%) No Diferencia de temperatura (°C) No Contracción volumétrica (%) No Flujo de calor en la pared del molde (W/m2) Sí 70 Desplazamiento en dirección X (mm) No Desplazamiento en dirección Y (mm) Sí 70 Desplazamiento en dirección Z (mm) No - Fuerza de cierre (Ton) 150 100 50 0 0 10 20 30 40 50 60 70 80 90 Temperatura de desmoldeo (ºC) 42 50 40 30 20 10 0 0 10 50 40 30 20 10 0 20 30 40 50 60 70 6 4 2 0 0 80 90 10 20 30 40 50 60 70 80 90 Nº de nodos en la entalla 1,2E+04 1,0E+04 Temperatura del refrigerante (ºC) Número de Reynolds 1,4E+04 8,0E+03 6,0E+03 4,0E+03 2,0E+03 0,0E+00 10 20 30 40 50 60 70 80 90 40 35 30 25 20 15 10 5 0 0 50 40 30 20 10 0 10 20 30 40 50 60 70 Nº de nodos en la entalla 10 20 30 40 50 60 70 80 90 Nº de nodos en la entalla 80 90 Temperatura de la masa al final del llenado (ºC) Temperatura de la pared del molde (ºC) Nº de nodos en la entalla 0 80 90 8 Nº de nodos en la entalla 0 60 70 10 Máximo esfuerzo de corte en procesamiento (MPa) Máximo esfuerzo de corte en cargas de servicio (MPa) 60 10 40 50 Nº de nodos en la entalla Nº de nodos en la entalla 0 20 30 300 250 200 150 100 50 0 0 10 20 30 40 50 60 70 80 90 Nº de nodos en la entalla Figura 5.5 Resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos triangulares. 120 100 80 60 40 20 0 0 10 20 30 40 50 60 70 80 90 Porcentaje de rechupe (%) Porcentaje total en peso (%) 43 2,5 2 1,5 1 0,5 0 0 10 20 100 80 60 40 20 0 0 10 20 30 40 50 60 70 80 90 30 40 50 60 70 80 90 Desplazamiento en X (mm) Contracción volumétrica (%) 20 0,20 0,15 0,10 0,05 0,00 30 40 50 60 70 Nº de nodos en la entalla 80 90 Desplazamiento en Z (mm) Desplazamiento en Y (mm) 0,25 20 80 90 0,4 0,3 0,2 0,1 0 0 10 20 30 40 50 60 70 80 90 0,30 0,25 0,20 0,15 0,10 0,05 0,00 0 10 20 30 40 50 60 70 80 90 80 90 Nº de nodos en la entalla 0,30 10 70 0,5 Nº de nodos en la entalla 0 60 Nº de nodos en la entalla 4 4 3 3 2 2 1 1 0 10 50 0,6 Nº de nodos en la entalla 0 40 Nº de nodos en la entalla Diferencia de temperatura (ºC) Presión al final del llenado (MPa) Nº de nodos en la entalla 30 0,05 0,04 0,03 0,02 0,01 0,00 0 10 20 30 40 50 60 70 Nº de nodos en la entalla Figura 5.6 Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos triangulares. 44 A partir de esto, se puede decir que los resultados de temperatura de desmoldeo, temperatura de la masa al final del llenado, temperatura de la pared del molde, flujo de calor en la pared del molde, porcentaje en peso y desplazamiento en la dirección “Y” presentan convergencia en todos los casos, mientras que la temperatura del refrigerante y el número de Reynolds convergen siempre. Por otra parte, los resultados correspondientes a diferencia de temperatura y desplazamiento en la dirección “Z” nunca presentan convergencia dentro del rango estudiado. Finalmente, existe una serie de resultados que dependiendo del caso de estudio exhiben o no convergencia, entre los cuales se encuentran el porcentaje de rechupe, fuerza de cierre, presión al final del llenado, contracción volumétrica y desplazamiento en la dirección “X”. Al analizar estos datos, es posible encontrar que aquellos resultados correspondientes a la fase de llenado de la pieza en la cavidad, no presentan ningún tipo de inconvenientes por lo que efectivamente pueden alcanzar la convergencia. No obstante, el problema es encontrado para los resultados vinculados a la fase de enfriamiento y contracción, además de la fuerza de cierre ejercida por la máquina de inyección. Esto es principalmente ocasionado, a que las curvas P-v-T elaboradas para los distintos materiales disponibles en la base de datos de C-MOLD, fueron realizadas bajo condiciones de compresión isotérmica y teniendo en cuenta únicamente a la temperatura del fundido y a la presión de inyección. En vista de esto, la velocidad de enfriamiento no fue tomada en consideración, por lo que los resultados obtenidos para el volumen específico en cada caso, no se corresponden a la realidad, lo cual puede ser evidenciado al observar la variación de las curvas de volumen específico en función de presión y temperatura, para diferentes velocidades de enfriamiento, como las realizadas por Pantani y Titomanlio [67], en donde éstas presentan grandes cambios en sus formas. Desde el punto de vista ingenieril, la influencia de las condiciones del proceso y particularmente de la velocidad de enfriamiento, ejercen un notable peso sobre el volumen específico, el cual a su vez es una importante propiedad del material, ya que éste determina la posible contracción o alabeo final de la pieza. Para el caso de piezas con espesores variables, la aproximación realizada por C-MOLD variará fuertemente, no obstante, para piezas con espesores relativamente uniformes, como las empleadas en este trabajo, la aproximación realizada no es tan incongruente, sin embargo, no es exacta y por ello se presentan los errores obtenidos y la no convergencia de estos resultados [68]. 45 Las gráficas correspondientes a las placas con entallas semicirculares, de donde fue suministrada la información anteriormente mostrada en la tabla 5.1 pueden ser encontradas en el Apéndice B. 5.2 DETERMINACIÓN DEL FACTOR DE CONCENTRACIÓN DE ESFUERZOS (Kt) Una vez llevado a cabo todo lo concerniente a los montajes de los distintos sistemas en el programa C-MOLD y de los posteriores procedimientos para la simulación en cada caso, se prosiguió a las mediciones de los diferentes resultados para esfuerzos reportados por el programa simulador. Entre los posibles criterios para el estudio del comportamiento plástico ideal en la mecánica clásica se puede encontrar el criterio de Tresca (ecuación 5.1), el cual fue el primer criterio desarrollado para describir el comportamiento a fluencia principalmente de metales y que propone que la fluencia ocurre cuando un valor crítico para el esfuerzo de corte σs es alcanzado. σs = (σ 1 − σ 3 ) ecuación 5.1 2 Adicionalmente, es posible encontrar el criterio de Coulomb (ecuación 5.2), el cual es propuesto por la literatura como más apropiado que el de Tresca para ser aplicado en polímeros. Este criterio está basado en la premisa de que el esfuerzo crítico de corte τ para fluencia ocurre en cualquier plano que varíe la linealidad con respecto al plano del esfuerzo normal, e incluye a un término llamado cohesión (τc) y al coeficiente de fricción interna (µ). τ = τ c − µσ N ecuación 5.2 Finalmente, el criterio de Von Mises (ecuación 5.3) asume que el comportamiento a fluencia es independiente de la presión hidrostática, así como que los esfuerzos de fluencia en tensión simple y compresión son iguales. Igualmente bajo este criterio puede ser expresado que la condición de fluencia ocurre cuando la energía de esfuerzo-deformación en el material alcanza un valor crítico que puede ser expresado como una relación simétrica de los esfuerzos principales [47, 69-70]. (σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 = Cons tan te ecuación 5.3 46 En función a lo anteriormente descrito, es necesario señalar que los resultados utilizados en este trabajo corresponden a los esfuerzos de Mises-Hencky tanto para cargas en servicio, como en procesamiento, los cuales a su vez están basados en el criterio para el comportamiento plástico en fluencia de Von Mises y que de acuerdo a lo señalado por Candal [65] , éste representa el esfuerzo más similar encontrado bajo el contexto real de piezas poliméricas, es decir, el que puede ofrecer los resultados más ajustados a la realidad, debido a que a diferencia de los demás modelos, este toma en consideración los esfuerzos en las tres direcciones principales “X”, “Y” y “Z”, hecho que toma mayor importancia al tratarse de piezas gruesas. Durante el análisis de resultados de los esfuerzos reportados por C-MOLD tanto para la variación de la geometría de las distintas entallas, como para la modificación de las condiciones de operación durante el proceso de inyección, se obtuvo que los esfuerzos de Mises-Hencky en cargas de servicio únicamente presentaron cambios para el primero de los casos, mientras que en aquellas simulaciones en las que fueron cambiados los parámetros de operación este esfuerzo en cargas de servicio permaneció prácticamente invariable. De igual forma, al analizar y tomar anotaciones de los esfuerzos de Mises-Hencky durante el procesamiento, fue posible encontrar un comportamiento exactamente opuesto al anterior, lo cual es un resultado completamente lógico debido a que este esfuerzo toma únicamente en consideración la orientación inducida sobre el material durante el proceso de inyección, así como aquellos esfuerzos internos que puedan ser generados, hecho que es precisamente lo que se pretende evaluar al realizar simulaciones en donde las condiciones de operación son modificadas. Sin embargo, hay que mantener en cuenta que la distribución final de esfuerzos estudiada sobre las distintas placas, comprende la influencia de ambos esfuerzos, tanto en cargas de servicio, como durante el procesamiento por lo que fue necesario establecer una expresión que permitiera de una manera u otra obtener una resultante o promedio de ambos valores. Esto es sumamente importante para polímeros debido a que al ser inyectadas las piezas, los efectos de orientación y llenado afectan las propiedades finales de las piezas. Por lo cual se deben sumar estos dos resultados para considerar el efecto del uso de la pieza con su fabricación. Para esto fue utilizada la siguiente expresión: 47 σ r = (σ servicio ) 2 + (σ proceso ) 2 ecuación 5.4 en donde: σservicio= Esfuerzo de Mises-Hencky en cargas de servicio reportado por C-MOLD(MPa) σproceso= Esfuerzo de Mises-Hencky en el procesamiento reportado por C-MOLD(MPa) σr= Esfuerzo de Mises-Hencky resultante (MPa) A continuación en la figura 5.7, es posible observar la distribución de esfuerzos presentados a lo largo del eje de posición de la entallas para placas con concentrador de 15 10 5 20 servicio (MPa) Esfuerzo en cargas de 20 servicio (MPa) Esfuerzo en cargas de esfuerzos de tipo semicircular y distinta geometría. -4 -2 0 2 4 10 5 0 0 -6 15 -6 6 -4 -2 10 5 2 4 15 10 5 0 0 0 -6 6 -4 -2 10 5 2 4 6 4 6 10 5 -6 6 -4 -2 0 2 Ub icació n e n la p laca (f) (e) 15 10 5 20 servicio (MPa) Esfuerzo en cargas de 20 sercicio (Mpa) 4 15 Ub icació n e n la p laca Esfuerzo en cargas de 6 0 0 0 4 20 servicio (MPa) Esfuerzo en cargas de 15 -2 2 (d) 20 servicio (MPa) Esfuerzo en cargas de (c) -4 0 Ub icació n e n la p laca Ub icació n e n la p laca -6 6 20 servicio (MPa) Esfuerzo en cargas de 15 -2 4 (b) 20 servicio (MPa) Esfuerzo en cargas de (a) -4 2 Ub icació n e n la p laca Ub icació n e n la p laca -6 0 15 10 5 0 0 -6 -4 -2 0 2 Ub icació n e n la p laca (g) 4 6 -6 -4 -2 0 2 Ub icació n e n la p laca (h) Figura 5.7 Distribución de esfuerzos en placas con entallas semicirculares y diferentes relaciones d/D: (a) 0.92, (b) 0.88, (c) 0.85, (d) 0.81, (e) 0.78, (f) 0.74, (g) 0.71 y (h) 0.67. 48 Al examinar esta serie de gráficas es posible notar que los mayores esfuerzos se encuentran ubicados en las zonas circundantes a los concentradores de esfuerzos. Este resultado es coincidente con lo presentado por Jiménez [49] para placas de PS y entallas triangulares. De igual manera, este hecho es debido a que al aplicar una carga o estar involucrado un concentrador de esfuerzos en una pieza, dicha discontinuidad provoca alteraciones en la distribución tensional, lo que provoca que el esfuerzo máximo disminuya progresivamente en la medida en que incrementa la distancia referente al punto de aplicación de la carga. Este comportamiento es definido como el Principio de Saint-Venant [14] . A continuación, en la figura 5.8 se presenta una representación de la distribución de esfuerzos para una placa con entalla circular, en donde claramente es posible observar la mayor intensidad (color rojo) en el área circundante al agujero. Figura 5.8 Esquema de distribución de esfuerzos de Mises-Hencky en una placa entallada. Seguidamente, en la figura 5.9 es presentada una gráfica en donde se puede verificar que los esfuerzos de Mises-Hencky en el procesamiento (verde), en cargas de servicio (rojo) y el esfuerzo resultante (azul) calculado a través de la ecuación 5.4, cumplen con la misma tendencia. 1,400 1,200 1,000 0,800 0,600 0,400 0,200 0,000 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 r/ D Figura 5.9 Verificación de tendencias descritas por los esfuerzos en el procesamiento, cargas de servicio y resultante. 49 Luego de obtenidas las magnitudes resultantes para los esfuerzos generados en las placas de PSAI con las diferentes entallas, se realizó el mismo procedimiento, pero en este caso para una placa estándar de las mismas dimensiones y sin ningún tipo de variación en su sección transversal. Esto fue llevado a cabo con el objetivo de obtener la información pertinente a los esfuerzos de Mises-Hencky existentes en la dirección de su eje, de donde finalmente el valor de uno de sus extremos fue utilizado como magnitud referente al esfuerzo máximo posible y cuyo valor constante obtenido de los ensayos corresponde a σmáx= 14,13 MPa. Es importante mencionar que es imprescindible trabajar con el esfuerzo máximo y no con un esfuerzo promedio, tanto en cargas de servicio como en el procesamiento, para analizar los resultados, ya que de esta manera es posible calcular posibles fallas presentes. Una vez extraída toda la información necesaria, se procedió a la aplicación de la ecuación 4.1, de donde fue posible entonces obtener el valor del factor Kt para cada caso de estudio. En el Apéndice C son mostrados todos los valores de Kt calculados en este trabajo, así como las condiciones involucradas en cada uno. 5.3 INFLUENCIA DE LA GEOMETRÍA DE LAS ENTALLAS SOBRE EL FACTOR DE CONCENTRACIÓN DE ESFUERZOS (Kt) Para el desarrollo de esta parte de la investigación, se pretendió evaluar la influencia o efecto que tiene la presencia de concentradores de esfuerzos en placas de PSAI, esto tomando en consideración cuatros distintas geometrías para las entallas (triangular, circular, semicircular y rectangular), así como diferentes dimensiones para cada uno de los casos. De acuerdo a lo descrito por Jiménez [49] , una vez calculados los valores correspondientes al Kt, es necesario realizar curvas de este factor en función de los parámetros geométricos d/D y r/d de cada una de las placas. El esfuerzo máximo para una placa sin entalla fue obtenido mediante la utilización de la ecuación 5.4 y mantenido como un valor constante e igual a σmáx= 14,13 MPa, el cual será utilizado en todos los tipos de placas entalladas por medio de la ecuación 4.1. En el Apéndice D, es posible observar un ejemplo de cálculo en donde se emplea éste valor. 50 5.3.1 Entallas triangulares En particular, en lo que se refiere al estudio de placas con concentradores de esfuerzos de tipo triangular, en la figura 5.10 son mostradas las curvas obtenidas para el factor Kt en función de los parámetros geométricos. 0,650 0,700 0,650 0,600 Kt Kt 0,600 0,550 0,550 0,500 0,450 0,400 0,30 0,40 0,50 0,60 0,70 0,80 0,90 0,500 0,10 0,20 0,30 d/D r/d (a) (b) 0,40 0,50 Figura 5.10 Curvas obtenidas para placas con entallas triangulares del factor Kt en función de: (a) d/D y (b) r/d. En la figura 5.10 (a) es representado el factor Kt en función de la relación geométrica d/D para una dimensión r constante, en donde en la medida en que esta relación se hace más grande implica que la dimensión d aumenta, ocasionado esto a que la altura h de las entallas disminuye, es decir, las entallas son cada vez más pequeñas. En éste caso, para valores pequeños de d/D es imposible observar un comportamiento específico, debido a que la concentración de esfuerzos es tan alta que es indiferente el tamaño de d/D, pero en la medida en que la relación d/D aumenta ya es posible apreciar una tendencia más clara, en donde el Kt incrementa ligeramente a medida que las entallas se hacen más pequeñas, esto debido a que los esfuerzos residuales van a aumentar nuevamente en vista de que las entallas cada vez se van a ser más agudas, lo que repercute en una reducción del esfuerzo tensil de la placa entallada, por lo que de acuerdo a la ecuación 4.1 va a acrecentar la magnitud de Kt [71]. . Por su parte, en la figura 5.10 (b) fue obtenida una relación para el Kt en función del coeficiente r/d para una dimensión d constante. Para este caso sí fue posible encontrar una tendencia clara a partir de la cual se puede afirmar que en la medida en que la relación r/d aumenta, el factor Kt también se incrementa. Este resultado es obtenido debido al hecho de que para los casos en que r/d es mayor, el ancho de la entalla se hace cada vez más grande, lo que causa que el tamaño lateral de ésta incremente, por lo que el polímero fundido al entrar a la cavidad se va a encontrar con una discontinuidad más abrupta, impidiendo así el libre flujo 51 de éste a través de la placa y por consiguiente, provocando una mayor concentración de esfuerzos, especialmente en las zonas cercanas a los ángulos agudos de la entalla. A partir de esto es posible concluir que para placas de PSAI con concentradores de esfuerzo de tipo triangular, en la medida en que el tamaño de la entalla aumenta en su dimensión r, el factor Kt será incrementado. De igual forma, el caso contrario también puede ser justificado, es decir, mientras el tamaño lateral de la entalla sea menor el factor Kt también disminuirá, por la menor concentración de esfuerzos originada. Al comparar los resultados obtenidos para el factor Kt durante este trabajo y para este caso, con los obtenidos por Jiménez en su investigación [49] , se consigue con el hecho de que en este último caso las magnitudes para los distintos factores Kt son mayores que los conseguidos a través de nuestras simulaciones. Sin embargo esto puede ser explicado a partir de la naturaleza química y comportamiento mecánico de los materiales empleados en cada caso. El material empleado por Jiménez [49] en sus experimentos fue un Poliestireno cristal (PS), el cual es un polímero rígido, duro y de naturaleza frágil, por lo que su curva esfuerzodeformación cumple con la ley de Hooke en todo su campo para ensayos de tracción. Este material está caracterizado por procesos de cavitación, en donde la capacidad de deformación se encuentra sumamente restringida, lo que es originado cuando las fuerzas cohesivas entre átomos son superadas por las solicitaciones externas inducidas. Durante este proceso son producidas micro-grietas que ponen de manifiesto la existencia de un componente de dilatación encontrado bajo condiciones de tensión. Debido a esto, el material no presenta un mecanismo de fluencia por lo que no es capaz de relajar tensiones residuales tan fácilmente, y de aquí que las magnitudes de concentración de esfuerzos sean altas y críticas. Por su parte, en el caso de esta investigación fue utilizado un PSAI, el cual corresponde a un polímero multiface basado en una matriz de PS reforzado con partículas de caucho, las cuales son capaces de controlar las condiciones bajo las cuales micro-grietas pueden ser producidas, por lo que de esta manera la deformación plástica dentro del material es incrementada, así como su capacidad de absorción de energía. Por tal razón, es que al utilizar este material las concentraciones de esfuerzos finales en piezas serán menores y por consiguiente, el factor Kt también será bajo [69, 72-73]. 52 5.3.2 Entallas circulares Para el caso de placas con entallas de tipo circular, solamente fue posible obtener una relación para el factor Kt en función del parámetro geométrico d/D, esto debido a que como la discontinuidad es encontrada justo en el punto central de la placa, no es posible establecer una dimensión r de acuerdo a lo presentado anteriormente en la figura 4.1. Igualmente para este caso, la distancia d tuvo que ser considerada mediante una relación del ancho total de la placa, menos la longitud correspondiente al diámetro de la entalla. En la figura 5.11 presentada a continuación, es posible observar una gráfica del factor Kt en función de la relación geométrica d/D, en donde en la medida en que esta relación aumenta, el factor Kt disminuye progresivamente. Este hecho puede ser traducido de manera de que a medida que el diámetro del agujero situado en el centro de la placa es mayor, los esfuerzos generados en ésta van a ser incrementados y por ende la resistencia tensil disminuye, lo cual a su vez puede ser apreciado en la figura 5.12, en donde se presentan los dos diámetros extremos para las entallas circulares empleados, con sus respectivas escalas de esfuerzos alcanzados. 0,700 Kt 0,650 0,600 0,550 0,500 0,60 0,70 0,80 0,90 1,00 d/D Figura 5.11 Curva obtenida para placas con entallas circulares del factor Kt en función de d/D. Figura 5.12 Esfuerzos registrados en placas con entallas circulares de diámetro: (a) 7 mm y (b) 28 mm. 53 Una posible explicación para esto, puede ser que en la medida en que el diámetro de la entalla presente en la placa sea más grande, va a existir una mayor probabilidad de que se pueda suscitar o inducir a un estado tridimensional de esfuerzos en ésta, por lo que la producción de crazes o micro-grietas va a ser un factor de riesgo a tener en consideración, ya que éstas pueden suprimir la capacidad de deformación plástica del material vía mecanismos de fluencia. De igual forma, si el tamaño del agujero es grande va a significar un cambio abrupto e importante en la dirección de flujo del polímero fundido dentro de la cavidad, por lo que los esfuerzos residuales generados van a ser mayores, mientras que si el diámetro de éste es disminuido, la trayectoria de flujo del material se va a suavizar, haciéndose más uniforme. Sin embargo, sería necesario llevar a cabo simulaciones en placas con entallas circulares de diámetros mayores con el objetivo de verificar si esta tendencia continúa presente. Así mismo, como ya ha sido mencionado con anterioridad estos cambios presentes en la superficie del material resultan en concentraciones de esfuerzos que pueden alcanzar altos esfuerzos locales. En este caso en particular, estos esfuerzos picos están situados únicamente en el área circundante al diámetro del agujero [52] y en el programa simulador C-MOLD pueden ser apreciados por los colores de mayor intensidad. En la figura 5.13 es posible observar una representación esquemática de lo anteriormente descrito. Figura 5.13 Distribución de esfuerzos alrededor de un agujero situado en una placa delgada infinita [52]. 5.3.3 Entallas semicirculares Seguidamente y bajo los mismos criterios de evaluación empleados en los casos anteriores, placas de PSAI con concentradores de esfuerzos de tipo semicircular fueron 54 estudiadas. A continuación en la figura 5.14 son presentadas las curvas correspondientes al factor Kt en función de los parámetros geométricos d/D y r/d. 1,150 1,090 1,085 Kt Kt 1,100 1,080 1,050 1,075 1,000 0,60 0,70 0,80 0,90 1,00 1,070 0,00 0,10 0,20 0,30 d/D r/d (a) (b) 0,40 0,50 0,60 Figura 5.14 Curvas obtenidas para placas con entallas semicirculares del factor Kt en función de: (a) d/D y (b) r/d. Al analizar la figura 5.14 (a) es posible afirmar que para concentradores de esfuerzos tipo semicirculares, el factor Kt describe un comportamiento constante como función de la relación geométrica d/D, ya que los valores resultantes de las simulaciones se encuentran muy cercanos entre si. Por otra parte, en lo que se refiere a la figura 5.14 (b) en donde es graficado el factor Kt en función de la relación r/d, se observa un evidente compromiso entre ambos valores. En esta oportunidad el factor Kt es alto a bajos valores de r/d, es decir, en aquellos casos en donde se trabaja con entallas pequeñas, tanto en su ancho como en su altura. Posteriormente, en la medida en que r/d se incrementa, el factor Kt disminuye su magnitud progresivamente hasta llegar a un punto a partir del cual este factor comienza a aumentar nuevamente mientras las entallas continúan haciéndose más grandes. La razón del comportamiento presentado en este caso, es debida a que para muy bajos valores de la relación r/d el radio de curvatura de la entalla es tan pequeño que ésta se torna aguda, por lo que entonces el polímero fundido dentro de la cavidad del molde al entrar en contacto con esta zona va a sufrir grandes esfuerzos de corte, por lo que la concentración de esfuerzos y consiguientemente, el factor Kt va a resultar alto. En la medida en que el radio de curvatura de la entalla es incrementado, ésta será menos aguda y por lo tanto, los esfuerzos generados serán de menor intensidad. Sin embargo, esta tendencia se mantiene hasta llegar a un punto crítico, a partir del cual el radio de curvatura de la entalla es tan grande que ya la entalla comienza a ser un obstáculo o restricción importante para el flujo del material. En este punto, la entalla ha incrementado tanto sus dimensiones que el polímero fundido al llegar a 55 ésta se encuentra con una pared que debe bordear, lo que produce nuevamente altas concentraciones de esfuerzos. Al comparar las curvas obtenidas para el factor Kt en función de la relación r/d en placas de PSAI, con las disponibles en la literatura para placas metálicas con concentradores de esfuerzos tipo “U” (Apéndice E), es posible observar una semejanza en el comportamiento presentado para ambas a bajos valores de r/d, no obstante para altos valores de esta relación los comportamientos cambian por completo. A partir de este hecho, se puede afirmar entonces que el factor Kt no depende únicamente de los parámetros geométricos establecidos para las entallas, ya que de ser así los comportamientos y tendencias deberían ser iguales en todo el rango de estudio, sino que también es una función de las condiciones de operación empleadas durante la fabricación de la pieza, así como del tipo y naturaleza del material seleccionado para su elaboración. 5.3.4 Entallas rectangulares Finalmente, el último tipo de concentrador de esfuerzos estudiado corresponde al de tipo rectangular y en la figura 5.15 es posible observar las curvas del factor Kt versus las relaciones geométricas obtenidas para este caso. 0,650 0,700 0,600 Kt Kt 0,650 0,600 0,550 0,550 0,500 0,30 0,40 0,50 0,60 0,70 0,80 0,90 0,500 0,10 0,20 0,30 d/D r/d (a) (b) 0,40 0,50 Figura 5.15 Curvas obtenidas para placas con entallas rectangulares del factor Kt en función de: (a) d/D y (b) r/d. De la relación para el factor Kt en función de d/D mostrada en la figura 5.15 (a), no fue posible obtener resultados contundentes en vista de que a partir de los puntos situados en la curva, no se puede establecer una tendencia clara. Sin embargo, para la figura 5.15 (b) se presenta un comportamiento comparable al descrito para placas con concentradores de esfuerzos de tipo semicirculares a bajos valores de r/d. El hecho de que esta relación 56 geométrica disminuya, implica que la entalla se va a hacer cada vez más aguda, provocando incrementos en los esfuerzos de corte registrados sobre el material, aunado a los distintos ángulos rectos existentes en la entalla, los cuales a su vez incrementan esta generación de esfuerzos. En caso contrario, a medida de que la entalla se haga más grande, lo que implica que la relación r/d aumente, los esfuerzos inducidos sobre el polímero van a ser cada vez de menor magnitud. El estudio de este tipo de concentradores de esfuerzos fue particularmente distinto al de los demás, debido a que a diferencia de las otras formas de entallas en las cuales los esfuerzos máximos se encontraban y fueron medidos exactamente en el vértice de ellas, para este caso los esfuerzos de Mises-Hencky máximos fueron encontrados en las zonas cercanas a los ángulos rectos que conforman la entalla y siendo de iguales magnitudes para ambos ángulos de la misma. En la figura 5.16, es posible apreciar una representación de la medición de los esfuerzos empleada a lo largo de una placa con entalla rectangular. Figura 5.16 Disposición de los esfuerzos de Mises-Hencky medidos en las placas con entallas rectangulares. Por último y a partir de todo lo anteriormente descrito, se puede recomendar el estudio posterior de placas con concentradores de esfuerzos triangulares de mayores relaciones r/d que las estudiadas durante este trabajo, así como evaluar y comparar entallas semicirculares y rectangulares con similares relaciones geométricas [50]. 57 5.4 INFLUENCIA DE LAS CONDICIONES DE OPERACIÓN SOBRE EL FACTOR DE CONCENTRACIÓN DE ESFUERZOS (Kt) Adicionalmente, en este trabajo se llevó a cabo una investigación referente al efecto de las condiciones de operación empleadas durante el proceso de inyección de las piezas, esto mediante la variación de la temperatura del fundido (Tf), presión sostenida (Psos), velocidad de inyección (Viny) y temperatura del líquido refrigerante (Tref). Es importante señalar, que al modificar cualquiera de las condiciones anteriormente presentadas todas las demás fueron mantenidas constantes, esto con la finalidad de poder realizar el estudio de una sola variable a la vez. De igual forma, los valores utilizados en todos los casos fueron seleccionados a partir de los presentes en la base de datos del programa simulador C-MOLD y teniendo en cuenta de que estuviesen dentro del rango de procesabilidad permisible para el material (PSAI), de manera que el proceso de inyección transcurriera sin eventualidades, así como evitando la posible degradación del polímero. 5.4.1 Temperatura del fundido En lo que se refiere a la temperatura del fundido, los valores utilizados durante las simulaciones fueron 190, 210, 230, 250 y 270 °C, los cuales se encuentran dentro del rango recomendado por C-MOLD para éste material en particular (176 a 273 °C). A partir de los resultados obtenidos se procedió a la construcción de curvas Kt en función de la temperatura del fundido, para una geometría de entalla constante en cada caso. El comportamiento presentado por las distintas curvas se encontró acorde con lo esperado teóricamente, ya que en la medida en que la temperatura del polímero fundido es incrementada, el factor de Kt disminuye progresivamente. Este hecho es debido a que altas temperaturas inducen a una mayor reacción molecular por parte del material, lo que a su vez provoca la reducción en los esfuerzos residuales. Este comportamiento es coincidente con los estudios realizados por Timm y Couts [74] , quienes señalan que esta menor concentración de esfuerzos ocurre producto de una disminución de la viscosidad del polímero, ya que se va a facilitar la relajación de la orientación inducida al flujo de material al entrar a la cavidad del molde. 58 De igual manera, otros estudios plantean que cuando la temperatura del fundido es muy baja, las moléculas al entrar en contacto con las paredes del molde se van a encontrar bajo grandes esfuerzos de corte, así como una alta orientación, ya que debido a la más alta viscosidad del polímero, se requerirá de una mayor presión para lograr que éste pase a través de los canales de flujo. Así mismo, a una temperatura menor el material va a solidificar más rápidamente, lo que a la vez provoca que el tiempo resultante para la relajación de estos esfuerzos sea bajo [71-75]. En la figura 5.17 son presentadas las curvas para el factor Kt con respecto a la temperatura del fundido para las cuatro distintas formas de concentrador de esfuerzos 0,800 0,800 0,700 0,700 0,600 0,600 Kt Kt estudiadas, con sus respectivos ajustes cuadráticos. 0,500 0,400 0,300 0,400 y = -3E-05x2 + 0,0106x - 0,4246 R2 = 0,8728 0,200 170 190 210 230 250 0,500 0,300 270 y = -2E-05x2 + 0,0086x - 0,1052 R2 = 0,914 0,200 170 290 190 210 230 250 270 290 Temperatura del fundido (ºC) Temperatura del fundido (ºC) (a) (b) 1,100 0,800 0,700 1,000 Kt Kt 0,600 0,900 0,800 170 0,400 y = 2E-05x2 - 0,0079x + 1,9075 R2 = 0,8249 190 210 230 250 0,500 0,300 270 Temperatura del fundido (ºC) 290 y = -1E-05x2 + 0,004x + 0,356 R2 = 0,9055 0,200 170 190 210 230 250 270 290 Temperatura del fundido (ºC) (c) (d) Figura 5.17 Curvas de Kt obtenidas en función de la temperatura del fundido para entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Como ya fue mencionado, en la medida en que la temperatura del fundido sea más alta, esto incrementará los movimientos vibracionales atómicos y moleculares, a la vez de que la viscosidad del material se verá disminuida, así mismo las moléculas en contacto con las paredes estarán menos orientadas, por lo que el tiempo y la efectividad de la relajación aumentarán. Así mismo, para mayores valores registrados de temperatura, el tiempo de enfriamiento para la pieza necesariamente va a ser incrementado, por lo que existe una adición en el tiempo de relajación disponible para el material [7, 51-52] . Con la disminución de 59 estos esfuerzos residuales y por consiguiente, del factor Kt, es posible afirmar que la pieza va a presentar una mayor resistencia y capacidad para soportar cargas al ser procesada a más altas temperaturas, hecho que concuerda con previas investigaciones llevadas a cabo por Chen y colaboradores [71]. Como es posible observar en las figuras 5.17 (a), (b) y (d), las curvas presentan exactamente el comportamiento descrito anteriormente, no obstante, para la curva correspondiente a la entalla circular los valores conseguidos para el factor de concentración de esfuerzos, resultaron estar muy cercanos entre sí, por lo que podría afirmarse que para valores encontrados dentro del rango de temperaturas estudiado el parámetro Kt permanece prácticamente constante. Sin embargo, puede existir otra variable que ejerce influencia sobre estos resultados y ésta es la fuerte línea de soldadura, que ha diferencia de los demás casos, en este tipo de geometría es encontrada. De acuerdo a trabajos presentados por Heidweiller y Van Der Zwet [53] , ésta línea de soldadura corresponde al punto más débil encontrado alrededor de la entalla y ocurre cuando el flujo de material fundido es separado por la presencia de un obstáculo presente en el molde, luego del cual los distintos frentes de flujo del polímero pueden encontrarse nuevamente [52]. No obstante, para este caso de estudio pasa a ser un punto muy crítico para las placas simuladas y ensayadas a tensión, debido a que sin importar la temperatura a la cual se realice la simulación del proceso de inyección, la línea de soldadura se va a mantener presente y casi invariable en cuanto a su agudez y dimensiones, lo que directamente ejerce influencia sobre la disminución de las propiedades mecánicas. De acuerdo a Morales y colaboradores [16], lo que se espera es que al incrementarse la temperatura del fundido, de igual manera aumente la resistencia de la línea de soldadura, por lo que las piezas presentarán una mayor resistencia tensil. Sin embargo, para éste caso en particular, será posible señalar que el rango de temperaturas utilizado, no fue suficiente para disminuir los efectos acarreados por la presencia de la línea de soldadura formada luego de la etapa de llenado. En la figura 5.18 se muestra la línea de soldadura presente en las placas con concentradores de esfuerzos circulares, ensayadas a la más baja y más alta temperatura del fundido. 60 (a) (b) Figura 5.18 Líneas de soldadura en placas con entallas circulares para distintas temperaturas del fundido: (a) 190 °C y (b) 270 °C. 5.4.2 Presión sostenida En lo que se refiere a la presión sostenida o de sostenimiento, ésta es aplicada sobre el material fundido, y tiene como finalidad la de compensar los posibles efectos de contracción y alabeo al enfriarse la pieza. Por lo general, esta presión se ejerce hasta que la entrada se solidifica, debido a que luego de esto el polímero fundido ya no podrá entrar ni salir de la cavidad. Es importante señalar que si se excede en aplicar esta presión, se pueden producir tanto rebabas, como una compactación tal que originará que las piezas se peguen en el lado fijo del molde [1-9]. Si un colchón de material está presente dentro de la máquina de inyección y el tiempo para la aplicación de la presión es suficiente, al incrementar la magnitud de la presión sostenida generalmente se aumenta también la orientación del material debido a dos razones principales. Primeramente, material adicional puede fluir dentro de la cavidad del molde con la finalidad de compensar los efectos de contracción o alabeo post moldeo, causados por el proceso de enfriamiento de la pieza, así mismo, este material adicional que está siendo inyectado provoca una alta orientación interna o del núcleo de la pieza, por lo general, en la zona cercana a la entrada. Por otra parte, altas presiones reducirán la relajación del polímero fundido por lo que la orientación y consecuentemente, los esfuerzos residuales serán conservados [40]. En la figura 5.19 presentada a continuación, son mostradas las curvas obtenidas para el factor de Kt en función de la presión sostenida, resultantes de las simulaciones para las placas entalladas y cuyo rango de valores estudiados se encontró entre 5 y 9 MPa. 0,800 0,800 0,700 0,700 0,600 0,600 Kt Kt 61 0,500 0,400 0,400 y = -0,001x2 + 0,0731x + 0,11 R2 = 0,9966 0,300 y = -0,0038x2 + 0,1043x + 0,1226 R2 = 0,9981 0,300 0,200 0,200 4 5 6 7 8 9 10 4 5 6 7 8 Presión sostenida (MPa) Presión sostenida (MPa) (a) (b) 9 10 0,800 1,200 1,100 1,000 0,900 0,800 0,700 0,600 0,700 0,600 Kt Kt 0,500 0,500 y =0,0022x2 - 0,0381x +1,1584 0,400 R2 =0,9618 0,300 y = -0,001x2 + 0,0613x + 0,1545 R2 = 0,9886 0,200 4 5 6 7 8 9 Presión sostenida (MPa) (c) 10 4 5 6 7 8 9 10 Presión sostenida (MPa) (d) Figura 5.19 Curvas de Kt obtenidas en función de la presión sostenida para entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. Al apreciar las curvas presentadas en la parte superior, así como los altos valores exhibidos por el R2, es posible notar que los puntos y las tendencias de comportamiento para las distintas entallas, se corresponden altamente a un ajuste cuadrático. De igual forma y consecuentemente con el comportamiento esperado teóricamente, a bajos valores de presión sostenida el material dentro de la cavidad del molde se va a encontrar menos compactado, lo que provoca un aumento en el volumen libre existente entre las cadenas poliméricas. Este hecho trae consigo una mayor facilidad para que el polímero pueda moverse y por lo tanto, relajar lo más posible todas aquellas orientaciones o esfuerzos remanentes que hayan podido formarse durante el proceso de llenado [51]. En la medida en que se va incrementando la magnitud de la presión de sostenimiento, este volumen libre es reducido debido a la mayor compactación del material dentro del molde, lo que dificulta a su vez el proceso de relajación de esfuerzos, ya que las cadenas poliméricas no van a tener la suficiente libertad, ni el tiempo necesario para reordenarse, lo cual coincide con la investigación realizada por Pantani y colaboradores [76], en donde se establece que en la medida en que la presión sostenida es mayor, la orientación molecular dentro de la muestra aumenta, por lo que más tiempo de relajación será necesario. Adicionalmente, al trabajar con una mayor presión sostenida, la presión en la cavidad también aumenta, debido a que la 62 transmisión de ésta es mucho mayor, lo que a su vez contribuye al más fuerte empaquetamiento del material y que puede ser evidenciado a través de mediciones de peso como las realizadas por Chen y Gao [77] , en donde se demuestra que el peso de la pieza aumenta con el incremento de la presión de sostenimiento. En consecuencia de lo anteriormente señalado, los esfuerzos residuales dentro de la pieza serán mayores, así como el factor Kt resultante de estos casos [51, 78-79]. De igual manera es necesario señalar, que la curva correspondiente a la figura 5.19 (c) y resultante de las simulaciones para placas con concentradores de esfuerzos de tipo circular, es la única que no sigue la tendencia anteriormente descrita. Para este caso los valores obtenidos del factor Kt se encuentran muy cercanos entre sí, por lo que los cambios son imperceptibles. Nuevamente es puesto de manifiesto la fuerte influencia que tiene la línea de soldadura producida durante el llenado de estas piezas, la cual fue descrita detalladamente en la sección anterior. 5.4.3 Velocidad de inyección La velocidad de inyección también fue una de las condiciones de operación cuyo efecto sobre las propiedades mecánicas de piezas inyectadas fue evaluado a través de simulaciones. Las máquinas de inyección están en la capacidad de operar y trasladar el polímero fundido hacia la cavidad del molde a distintas velocidades, de las cuales generalmente las más rápidas permiten el moldeo de piezas de pared delgada, a la vez de que pueden reducir el tiempo de ciclo. Este parámetro está referido a la máxima velocidad con que la unidad de inyección es capaz de alimentar el material hacia el molde, es decir, se puede definir como el volumen de material que entra a la cavidad por unidad de tiempo durante el período de inyección. Esta velocidad es una función directa de la capacidad hidráulica de bombeo de la máquina, así pues, la velocidad de flujo hidráulico controla la velocidad de inyección, mientras que la presión hidráulica controla la presión de inyección [7-40]. . De igual forma, el nivel o intensidad de la velocidad de corte ( γ ) impuesto sobre el material durante la etapa de llenado se encuentra directamente relacionado con esta variable. 63 De esta manera se espera que para los más altos valores de caudal de inyección, la temperatura de la masa de polímero fundido al final del llenado sea incrementada, lo que trae consigo una baja conducción de calor y probablemente, una más alta disipación de éste [80]. De acuerdo a lo establecido en la literatura, altas velocidades de inyección pueden inducir a una mayor orientación en la superficie de las piezas y menor orientación en el núcleo, esto debido a los más grandes esfuerzos de corte producidos cerca de la pared del molde. Por otra parte, bajas velocidades de inyección minimizan la orientación en la superficie, mientras que el núcleo resulta más altamente orientado que incluso cuando se trabaja con altas velocidades, sin embargo, en este caso el molde tiene más tiempo para enfriar al fundido mientras éste fluye a través de la cavidad, por lo que una mejor distribución de la orientación es producida y los esfuerzos residuales son disminuidos. No obstante si se trabaja con muy bajas magnitudes de velocidad, lo que correspondería a casos extremos, el polímero puede solidificarse antes de tiempo y no llenar completamente el molde [40-81]. En la figura 5.20 son presentadas las curvas referentes a la influencia de la velocidad 0,800 0,800 0,700 0,700 0,600 0,600 Kt Kt de inyección sobre el factor Kt en placas con distintas geometrías de entallas. 0,500 0,400 0,500 y = 0,0007x2 - 0,0134x + 0,6204 0,400 R2 = 0,9981 0,300 0,300 0,200 y = 0,0006x2 - 0,0094x + 0,7416 R2 = 0,9749 0,200 4 5 6 7 8 9 4 5 6 7 8 Velocidad de inyección (cm/s) Velocidad de inyección (cm/s) (a) (b) 1,100 9 0,800 0,700 1,000 Kt Kt 0,600 0,900 0,500 y = 0,0015x2 - 0,0218x + 1,0973 0,400 R2 = 0,92 0,300 y = -0,0012x2 + 0,0169x + 0,4829 R2 = 0,3022 0,200 0,800 4 5 6 7 8 9 4 5 6 7 8 Velocidad de inyección (cm/s) Velocidad de inyección (cm/s) (c) (d) 9 Figura 5.20 Curvas de Kt obtenidas en función de la velocidad de inyección para entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. 64 A pesar de lo esperado teóricamente, en donde la velocidad de inyección induce una mejor transferencia de la presión en el molde, a la vez de que en la medida en que aumenta ésta velocidad se van a producir mayores esfuerzos de corte y calentamiento viscoso, por lo que la temperatura del fundido incrementa [40] , para las simulaciones realizadas durante este trabajo no fue posible obtener un comportamiento o tendencia apreciable, en vista de que para todos y cada uno de los casos evaluados las magnitudes para el factor de Kt se mantuvieron casi constantes. Este hecho trae consigo dos premisas, una primera hipótesis que establece que el rango de velocidades empleado (4,5 – 8,5 cm/s) para llevar a cabo las distintas simulaciones no fue suficiente como para obtener cambios apreciables en la concentración de esfuerzos por parte del material, por lo que se puede recomendar la continuación de esta investigación mediante la simulación de nuevos casos que impliquen mayores velocidades. Así mismo, como segunda posible explicación para este comportamiento es viable plantear que la velocidad de inyección sea una de las variables del proceso de inyección que menos influencia imparta sobre este tipo de resultados. 5.4.4 Temperatura del refrigerante Finalmente, la última variable estudiada corresponde a la temperatura del líquido refrigerante, el cual fue agua pura en cada una de las simulaciones realizadas. De igual manera, las magnitudes utilizadas fueron 25, 35 y 48 °C, las cuales se encuentran dentro del rango permisible de funcionalidad recomendado para el PSAI, el cual es de 21 a 48 °C. Para la evaluación de este parámetro es necesario tener en cuenta los principios básicos de transferencia de calor. El calor fluye desde un cuerpo que se encuentra a más alta temperatura hacia uno con menor temperatura, lo cual es conocido como diferencia de temperaturas y en la medida en que esta diferencia sea mayor, la transferencia de calor entre los cuerpos va a aumentar. En el caso de operaciones de moldeo por inyección, la transferencia de calor por conducción tiene una vital importancia, debido a que tanto el material de fabricación del molde como el sistema de refrigeración incluido en su interior contribuyen a la conducción del calor desde el plástico fundido hacia las paredes del molde. Posteriormente, luego de que 65 el equilibrio térmico es alcanzado, el calor fluye en dirección inversa con el objetivo de mantener a la pieza moldeada al nivel deseado [40]. 0,600 0,600 Kt 0,800 Kt 0,800 0,400 0,400 y = 1E-05x2 - 0,006x + 0,7628 R2 = 1 0,200 y = -9E-06x2 - 0,0039x + 0,8113 R2 = 1 0,200 20 25 30 35 40 45 50 20 25 30 35 40 45 50 Temperatura del refrigerante (ºC) Temperatura del refrigerante (ºC) (a) (b) 0,800 1,000 0,600 Kt Kt 1,200 0,800 0,400 y = -7E-05x2 + 0,007x + 0,8363 R2 = 1 y = -3E-05x2 - 0,0021x + 0,6548 R2 = 1 0,200 0,600 20 25 30 35 40 45 Temperatura del refrigerante (ºC) 50 20 25 30 35 40 45 50 Temperatura del refrigerante (ºC) (d) (c) Figura 5.21 Curvas de Kt obtenidas en función de la temperatura del líquido refrigerante para entallas de tipo: (a) Triangular, (b) Semicircular, (c) Circular y (d) Rectangular. En la figura 5.21 anteriormente mostrada es posible observar la tendencia presentada por el factor Kt en función de la temperatura del líquido refrigerante. Para las curvas 5.21 (a), (b) y (d), se observa que en la medida en que la temperatura de refrigerante empleado es más baja, la diferencia de temperaturas entre el molde de inyección y el material fundido que está dentro de la cavidad del molde va a ser mayor, esto origina que la transferencia de calor aumente por lo que el enfriamiento de la pieza va a ocurrir de una manera más rápida, al comparar todas las condiciones. Debido a esto, para bajas magnitudes de temperatura del refrigerante la pieza va a solidificar en un menor tiempo por lo que las tensiones y esfuerzos inducidos durante la inyección del material van a ser congeladas, imposibilitando su efectiva relajación. Mientras que en el caso contrario, cuando el refrigerante se encuentra a una temperatura mayor, la pieza va a necesitar de más tiempo para enfriarse por lo que las cadenas poliméricas van a poder ejercer un mayor proceso de relajación, lo cual es coincidente con la investigación realizada por Chen y colaboradores [71] , en donde se afirma la obtención de mayores propiedades tensiles en una pieza que fue elaborada mediante una mayor temperatura del refrigerante o del 66 molde, debida a la menor concentración de esfuerzos residuales. Para el caso de la placa con entalla circular nuevamente no se apreció ningún efecto significativo, por lo que los resultados obtenidos permanecen prácticamente constantes. 5.5 DESARROLLO DE UNA METODOLOGÍA Y ELABORACIÓN DE ECUACIONES CONSTITUTIVAS PARA EL FACTOR DE CONCENTRACIÓN DE ESFUERZOS (Kt) Luego de haber estudiado y analizado todos los resultados anteriormente expuestos, se procedió al desarrollo de un modelo que ajustara y relacionara el factor Kt tanto a la geometría presentada por las piezas, como a las condiciones de operación más influyentes dentro del moldeo por inyección de plásticos. En vista de que no existen expresiones para describir el comportamiento del factor Kt, fue necesario primeramente establecer una metodología para ser aplicada durante este estudio. 5.5.1 Revisión bibliográfica Una gran cantidad estudios han sido realizados, con la finalidad de desarrollar modelos matemáticos que puedan describir las relaciones de esfuerzo-deformación presentes en los materiales, por lo que éstos serán tomados como punto de partida para este trabajo. Entre las diferentes investigaciones y expresiones elaboradas, es posible señalar el estudio realizado por Johnson y Cook [56-60] , los cuales inicialmente propusieron un modelo constitutivo fenomenológico que describe el comportamiento plástico de metales dúctiles y en donde se establece que el esfuerzo presenta dependencia con respecto a la deformación, velocidad de deformación y temperatura durante la deformación plástica en materiales metálicos. De igual manera, los primeros estudios referidos al área de los polímeros fueron llevados a cabo mediante combinaciones aditivas de las leyes de Hooke y Newton, debido al comportamiento viscoelástico que caracteriza a este tipo de materiales [60]. Posteriormente, se han realizado otras investigaciones como la de G´Sell y Jonas [55] , quienes propusieron un modelo de ecuación constitutiva para el comportamiento a esfuerzo-deformación de polímeros semicristalinos, en donde es integrada la viscoelasticidad y la viscoplasticidad en 67 una única expresión, sin embargo, éste tiene como principal limitación la de no poder ser aplicada a polímeros amorfos. De igual manera y con motivo de solventar la limitación antes presentada, Matsuoka [54] estableció una ecuación constitutiva para predecir el comportamiento de polímeros amorfos. A través de éste modelo, es posible representar la viscoelasticidad no lineal, fluencia y comportamiento a deformación, no obstante, no se ajusta correctamente al trabajar con grandes deformaciones. Adicionalmente y de acuerdo a lo establecido en la literatura para el desarrollo de ecuaciones constitutivas a partir de curvas esfuerzo-deformación, dos tipos de modelos analíticos son propuestos para su aplicación en polímeros sólidos: el de tipo aditivo y el de tipo multiplicativo. En el primer caso, la influencia de la deformación y de la velocidad de deformación es separada de manera aditiva, como se muestra a continuación [55, 81-85]: • • σ (ε , ε ) = f (ε ) + g (ε ) ecuación 5.5 mientras que para el modelo multiplicativo se tiene lo siguiente: • • σ (ε , ε ) = f ′(ε ) * g (ε ) ecuación 5.6 La escogencia de expresiones multiplicativas o aditivas no constituye un verdadero inconveniente, debido a que ambos sistemas no son más que expresiones elaboradas a partir de un mismo set de resultados y condiciones previamente evaluadas. No obstante, para este trabajo se utilizó un modelo multiplicativo, ya que según lo expuesto por G´Sell y Duffo [61] , este tipo de sistemas son más convenientes para ser utilizados en programas de computación, a la vez de que expresiones de este tipo presentan analogía con la ley de Norton-Hoff usualmente considerada para metales. Como ya fue mencionado anteriormente, no existen ecuaciones constitutivas que describan al factor Kt, por lo que se decidió partir de este tipo de modelos analíticos para éste desarrollo, y en donde la expresión general que interpreta el comportamiento de éste factor tiene la siguiente forma: K t = f (Geometría) * g (Corrección) ecuación 5.7 68 y la función de corrección presenta dependencia de las condiciones de operación utilizadas en el moldeo por inyección: g (Corrección) = g (T f , Psos , Tref ,Viny ) ecuación 5.8 Finalmente, entre los criterios o suposiciones presentes para el desarrollo del modelo en cuestión se encuentran los siguientes [62, 64-65]: • La deformación es local y homogénea en todo el material. • Los esfuerzos a través de la dirección del espesor son despreciables. • El material es incompresible (λ1λ2λ3 = 1). • El factor de concentración de esfuerzos cumple con una función multiplicativa. • Cada una de las variables de inyección tomadas en consideración para este estudio, son independientes unas de otras. • El efecto de la velocidad de inyección sobre el factor Kt se puede considerar como despreciable. • Tanto la temperatura del fundido como la temperatura del refrigerante cumplen con un ajuste de tipo Arrhenius. 5.5.2 Elaboración de gráficas tipo Arrhenius para las temperaturas del fundido y del líquido refrigerante Es importante señalar que el comportamiento tanto para la temperatura del fundido, como para la temperatura del líquido refrigerante fue establecido mediante una correlación y ajuste que sigue la ley de Arrhenius, por lo que para este caso el factor Kt es tratado como una variable de un sistema determinado para un amplio rango de valores de temperatura [86]. Para realizar estos ajustes, primeramente fue necesario convertir los valores correspondientes a las distintas temperaturas que se encontraban en °C a sus equivalentes magnitudes en °K. Seguidamente, fueron elaboradas gráficas de Ln (Kt) en función de 1/Temperatura (fundido o líquido refrigerante dependiendo del caso), esto con la finalidad de poder obtener de la pendiente de la ecuación, la constante necesaria para poder ser incluida posteriormente en el desarrollo matemático. En la figura 5.22 se muestra un ejemplo de gráfica tipo Arrhenius, para un caso en particular. 69 -0,0034 -0,00335 -0,0033 -0,00325 -0,0032 -0,00315 -0,0031 0 -0,1 Ln (Kt) y = -670,45x - 2,5911 2 R = 0,9968 -0,2 -0,3 -0,4 -0,5 -0,6 -1/T re f (1/°K) Figura 5.22 Ln (Kt) en función de 1/T refrigerante, para una placa con entalla semicircular. Finalmente, la expresión obtenida de este desarrollo y a ser utilizada en la ecuación constitutiva, presenta la siguiente forma: m Kt = e T ecuación 5.9 en donde m corresponde al valor de la pendiente reportado por el ajuste lineal realizado en EXCEL y T a la temperatura del polímero fundido o del líquido refrigerante. 5.5.3 Obtención de las expresiones cuadráticas resultantes de cada una de las relaciones graficadas para el factor Kt, como función de las distintas condiciones evaluadas Como siguiente paso a seguir para el desarrollo de las ecuaciones constitutivas, fue necesaria la elaboración de todas las gráficas pertinentes al factor Kt como función de las distintas condiciones simuladas, tanto para variación de la geometría de las entallas, como para aquellas placas en las que fueron cambiadas las condiciones de operación. Seguidamente, se le realizó a cada curva un ajuste cuadrático mediante el empleo de EXCEL, con el propósito de obtener las ecuaciones características de cada una, y de ellas los coeficientes requeridos para ser introducidos como semillas o valores iniciales en el programa ORIGIN. En la figura 5.23, es posible observar las curvas elaboradas para un caso en particular, además de que son señalados los distintos coeficientes extraídos de cada una de las relaciones cuadráticas. Adicionalmente, es importante señalar que este procedimiento fue llevado a cabo de igual manera en todas las geometrías de concentradores de esfuerzos estudiadas. Todas las condiciones evaluadas para el factor Kt durante este trabajo fueron graficadas, no obstante para la elaboración del modelo constitutivo únicamente fueron 70 empleadas la relación geométrica d/D, la presión sostenida y las temperaturas del fundido y del líquido refrigerante. Por su parte, la relación r/d no fue incluida debido a que ésta no puede ser calculada en placas con concentradores de esfuerzos tipo circulares, mientras que la velocidad de inyección fue considerada como poco influyente. 1,150 0,800 0,700 Kt 0,600 Kt 1,100 1,050 0,500 0,400 P1 P2 2 P3 1,000 0,60 P4 2 P5 P6 y = -9E-06x - 0,0039x + 0,8113 0,300 y = 0,6215x - 1,0043x + 1,4794 0,200 0,70 0,80 0,90 1,00 20 d/D 25 30 (a) 40 45 50 (b) 0,800 0,800 0,700 0,700 0,600 0,600 Kt Kt 35 Tem peratura del refrigerante (ºC) 0,500 0,400 0,500 0,400 P7 0,300 P8 2 P9 0,200 4 5 6 7 8 9 P10 0,300 y = -0,0038x + 0,1043x + 0,1226 10 0,200 170 Presión sostenida (MPa) 2 P11 P12 y = -2E-05x + 0,0086x - 0,1052 190 210 230 250 270 290 Tem peratura del fundido (ºC) (c) (d) Figura 5.23 Relaciones graficadas para placas con entallas semicirculares y coeficientes importantes. 5.5.4 Desarrollo de expresiones cuadráticas e iteraciones, mediante el empleo del Software ORIGIN El ajuste matemático fue realizado mediante la utilización del programa computacional ORIGIN, el cual está basado principalmente en modelos Newton-Rapsom. Esto tuvo como finalidad, el poder lograr la obtención de expresiones estandarizadas y bien definidas, aún sin haber contado con programas simuladores o sin haber realizado medidas experimentales y ensayos mecánicos a placas plásticas reales. Primeramente fueron introducidos los valores correspondientes a Kt y d/D al programa, tal como se puede observar en la figura 5.24 (a) y seguidamente, fue seleccionado el módulo para sistemas no lineales encontrado en la barra de herramientas (figura 5.24 (b)). Posteriormente y ya dentro de éste módulo, se creó un modelo de ecuación cuadrática genérica del tipo Kt = Ax2*Bx*C3 (figura 5.24 (c)). 71 (a) (c) (b) Figura 5.24 Pasos para el establecimiento de un modelo de ecuación cuadrática en ORIGIN: (a) Introducción de datos, (b) Módulo para sistemas no lineales y (c) Ecuación cuadrática genérica. A continuación, se introdujeron al sistema semillas o valores iniciales bajo las cuales comenzarían las distintas iteraciones. Es importante recordar que estos valores corresponden a las constantes obtenidas de las ecuaciones o ajustes cuadráticos mostrados en la parte anterior y más específicamente a los correspondientes a P1, P2 y P3 (ver figura 5.25 (a)). En este punto, se procedió a llevar a cabo el proceso de iteraciones, con la finalidad de conseguir los resultados que más se ajustaran al comportamiento de las variables introducidas. Esto puede ser apreciado seguidamente en la figura 5.25 (b). (a) (b) Figura 5.25 (a) Establecimiento de valores iniciales en ORIGIN y (b) Iteraciones. De estas iteraciones, el programa arroja tres resultados, los cuales van a corresponder a las nuevas constantes A, B y C que componen la expresión cuadrática genérica y que va a ser empleada en el próximo paso. Inmediatamente, se procede a repetir toda la metodología ya expuesta, pero en este caso se va a trabajar con los resultados de temperatura del líquido 72 refrigerante. Es necesario hacer la acotación, de que en esta oportunidad la expresión que va a ser introducida en ORIGIN presenta la forma Kt = (Ax2*Bx*C3)*f(x)*(expm/T), en donde f(x) es una magnitud constante obtenida luego de sustituir el valor de d/D fijo con el cual se realizaron los ensayos para variación de las condiciones de operación. Por su parte, el otro término de la expresión (ecuación 5.9), fue obtenido con anterioridad a través del ajuste de Arrhenius para estas temperaturas. Una vez llevado a cabo todo esto, se obtendrán tres nuevas constantes con las que se repetirá el procedimiento, ahora para la presión sostenida y luego tres constantes finales, con las que se trabajará la temperatura del fundido. Para terminar, a partir de la última ecuación conseguida se desglosan los términos involucrados en la expresión, por separado y de manera regresiva hasta lograr un modelo en donde se puedan apreciar las distintas variables involucradas en el proceso. Finalmente, la expresión general resultante o modelo para la ecuación constitutiva obtenida en este trabajo tiene la siguiente forma: [ ][ ] J K d 2 T T d 2 2 K t = A + B + C * D(Psos ) + E (Psos ) + F * G(T f ) + H (T f ) + I * exp ref * exp f D D ecuación 5.10 De igual manera, en la tabla 5.3 presentada a continuación, se muestran los valores correspondientes a las constantes expresadas en la ecuación constitutiva, para cada geometría de concentrador de esfuerzo. Tabla 5.3 Magnitudes correspondientes a cada constante expresada en la ecuación constitutiva para los diferentes concentradores de esfuerzo estudiados. Geometría Constantes Triangular Rectangular Circular Semicircular A 10,428 8,823 -0,826 5,106 B -12,626 -12,185 1,200 -8,241 C 13,295 11,828 -0,089 12,786 D -2,00E-3 -1,77E-03 3,53E-03 -3,66E-03 E 0,126 0,109 -0,063 0,099 F 0,193 0,271 1,969 0,107 G -3,00E-04 -2,10E-04 4,08E-06 -1,40E-04 H 0,254 0,176 -0,004 0,131 I -53,318 -26,929 1,679 -25,931 J -866,38 -802,03 191,23 -670,45 K -863,99 -1051,60 119,85 -718,73 73 Tal y como es posible observar en el modelo de ecuación constitutiva, ésta solamente es dependiente de la relación geométrica d/D, de la presión sostenida y de las temperaturas del fundido y del líquido refrigerante. Para este caso no se incluyó a la velocidad de inyección a pesar de que fue una de las variables de operación estudiada, y esto es debido a que como ya pudo ser apreciado con anterioridad en la figura 5.20, el factor Kt permaneció prácticamente invariable en todas las simulaciones realizadas para las distintas velocidades en cada uno de los concentradores evaluados. A partir de esto, fue posible entonces descartar este parámetro de operación como posible variable dentro de la ecuación desarrollada, ya que su influencia es despreciable al ser comparada con los demás parámetros. Seguidamente en la figura 5.26, se presentan gráficamente los resultados obtenidos para el factor Kt obtenido de las simulaciones (calculado a través de la ecuación 4.1) y del factor Kt teórico calculado a partir de la ecuación constitutiva desarrollada para las diferentes placas entalladas, evaluadas bajo condiciones de operación constantes y variación de la geometría de las entallas en sus dimensiones principales. De igual manera, son presentados los errores promedios resultantes entre ambas magnitudes. 0,80 0,80 Error Promedio = 3,69% Error Promedio = 2,24% 0,70 Kt Kt 0,70 0,60 0,60 0,50 0,50 0,40 0,40 0,3 0,4 0,5 0,6 0,7 0,8 0,3 0,9 0,4 0,5 d/D Simulación Simulación Teórico 0,7 0,8 0,9 Teórico (b) (a) 1,20 1,20 1,00 1,00 Error Promedio = 44,03% 0,80 Kt Kt 0,6 d/D 0,60 Error Promedio = 32,22% 0,80 0,60 0,40 0,40 0,3 0,4 0,5 0,6 0,7 0,8 (c) 1,0 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 d/D d/D Simulación 0,9 Teórico Simulación Teórico (d) Figura 5.26 Factor de concentración de esfuerzos obtenido de manera simulada y teórica para placas con entallas de tipo: (a) Triangular, (b) Rectangular, (c) Circular y (d) Semicircular. 74 Como es posible observar en las gráficas anteriormente mostradas, las magnitudes obtenidas para el factor Kt teórico y de las simulaciones, para placas con entallas de tipo triangular y rectangular, resultaron estar muy cercanas entre sí lo cual es evidenciado con mayor claridad a través de los errores promedios reportados para estas series de datos. A partir de este hecho sería posible afirmar que para placas con este tipo de concentradores de esfuerzos, la ecuación constitutiva desarrollada se ajusta bastante bien y arroja resultados acordes con los reales, o para este caso, con los obtenidos mediante el empleo de simuladores. Sin embargo, al analizar las curvas correspondientes a placas con concentradores de esfuerzos de tipo circular y semicircular, el error promedio entre estas mediciones resulta ser alto por lo que las magnitudes calculadas para el factor Kt a través de la ecuación constitutiva no concuerdan con los valores reales, aunque esto ocurre únicamente para los casos en que se varía la geometría de las entallas (Apéndice C). Este hecho es debido a que el modelo que está siendo planteado durante este trabajo está basado en la suposición inicial de que las condiciones de operación del proceso de inyección son independientes unas de otras, lo cual es una afirmación incorrecta, ya que todas estas variables de una u otra manera forman parte de un conjunto o sumatoria de influencias durante el proceso de transformación y cada una ejerce un efecto sobre el total. Como ejemplo a esto es posible mencionar efectos conocidos tales como, al incrementar la velocidad de inyección, directamente los esfuerzos de corte ejercidos sobre el material se elevan, lo cual sumado al mayor calentamiento por disipación viscosa, va a influir sobre el polímero incrementando la temperatura del fundido. De igual manera, el hecho de aumentar la velocidad de inyección implica que la presión de inyección también deberá ser más alta y por consiguiente, la magnitud de presión sostenida a utilizar incrementará. No obstante y a pesar de lo anteriormente justificado, es posible afirmar que las ecuaciones constitutivas desarrolladas para los distintos casos de estudio presentan un alto nivel de validez, debido a que en el caso de las placas con concentradores de esfuerzos de tipo triangular y rectangular la diferencia promedio entre los factores Kt simulados y teóricos obtenidos es menor al 10%, la cual es una muy buena aproximación, mientras que para el caso de placas con entallas semicirculares y circulares, el error es igualmente bajo al utilizar placas con relaciones geométricas de 0,81 y 0,92 respectivamente (Apéndice C). Los errores más 75 elevados que pudieron ser observados en las figuras 5.26 (c) y (d), corresponden únicamente a los resultados conseguidos para la variación de las distintas relaciones d/D, sin embargo, si se estudia el asunto a mayor profundidad se encontrará que un error del 40% para una placa entallada cuyo factor Kt es de aproximadamente 1,096 (la cual fue la mayor magnitud calculada entre todas las condiciones), no implica una diferencia trascendental en la capacidad para soportar cargas o esfuerzos en una pieza elaborada con PSAI. Finalmente, el desarrollo y construcción de un modelo de ecuación constitutiva para el cálculo del factor Kt en piezas plásticas, puede y deberá ser refinado, por lo que dentro de esto será necesario mantener presente los distintos efectos que tienen las condiciones de operación entre sí. Sin embargo, a partir de los estudios e investigación realizada, ha sido posible proponer un esquema de trabajo para la obtención del factor Kt a través de herramientas CAD/CAE, así como hacer de conocimiento la influencia de este factor sobre piezas con distintas geometrías de entallas, además de tener en cuenta cuáles condiciones de operación ejercen o presentan una mayor influencia sobre este parámetro. CAPÍTULO VI CONCLUSIONES Y RECOMENDACIONES 6.1 CONCLUSIONES • Es de vital importancia el establecimiento de un criterio para la convergencia en simulaciones realizadas mediante sistemas CAE, debido a que a través de éste será posible la obtención de resultados precisos y ajustados a la realidad. • Los resultados utilizados y que fueron proporcionados por el programa C-MOLD para el análisis de convergencia fueron el tiempo de ciclo, tiempo de llenado, esfuerzos de corte en la pared antes del tiempo de llenado y esfuerzo promedio en cargas de servicio, no obstante luego de llevar a cabo este estudio en base a otros resultados y para dos geometrías distintas de concentradores, se encontró que no todos presentan convergencia bajo las mismas condiciones. • Resultados como la temperatura de desmoldeo, temperatura de la masa al final del llenado, temperatura de la pared del molde, flujo de calor en la pared del molde, porcentaje en peso y desplazamiento en dirección “Y”, presentaron rápida convergencia en ambos casos de estudio, mientras que la temperatura del líquido refrigerante y el número de Reynolds convergen desde el principio en todo el rango de elementos simulado. • Los resultados correspondientes a diferencia de temperatura y desplazamiento en la dirección “Z” nunca presentaron convergencia dentro del rango estudiado, mientras que resultados como el porcentaje de rechupe, fuerza de cierre, presión al final del llenado, contracción volumétrica y desplazamiento en la dirección “X”, convergen dependiendo del caso evaluado, esto debido al problema de sobreestimación de la contracción y fuerza de cierre presente en C-MOLD. • Para el cálculo del factor Kt mediante la utilización de herramientas CAD/CAE, es necesario tomar el σmax como el esfuerzo de Mises-Hencky (en cargas de servicio y 77 procesamiento) reportado por C-MOLD para una placa sin entalla, a la vez de que σnom como el esfuerzo de Mises-Hencky para las distintas placas entalladas. • Para el caso de placas con entallas triangulares, en la medida en que el tamaño de la entalla disminuye en su dimensión h, el factor Kt incrementa ligeramente, mientras que si la dimensión r es mayor, el factor Kt también aumenta. • Para el caso de placas con entallas rectangulares, a medida de que la entalla se haga más grande, lo que implica que la relación r/d aumente, el factor Kt va a disminuir. • Para el caso de placas con entallas circulares, en la medida en que la relación geométrica d/D aumenta, el factor Kt disminuye progresivamente. • Para el caso de placas con entallas semicirculares, existe un compromiso entre el factor Kt y la relación r/d, ya que éste es alto para valores pequeños y grandes de r/d mientras que su magnitud disminuye para valores intermedios de la relación geométrica. • Al comparar las curvas del factor Kt en función de las relaciones geométricas obtenidas en placas con entallas semicirculares, con las existentes para placas metálicas con concentradores de tipo “U”, es posible observar diferencias entre éstas, con lo cual se puede afirmar que para polímeros el Kt no es solo dependiente de la geometría del concentrador sino también de las condiciones de operación. • Al aumentar la temperatura del polímero fundido, el factor Kt disminuye progresivamente en placas con entallas triangulares, rectangulares y semicirculares. Para placas con entalla circular, el factor Kt se mantiene prácticamente invariable. • Con el incremento de la magnitud de la presión sostenida, el factor Kt aumenta en placas con entallas triangulares, rectangulares y semicirculares. Para placas con entalla circular, el factor Kt se mantiene prácticamente invariable. • Para las simulaciones realizadas mediante la variación de la velocidad de inyección, el factor Kt se mantuvo prácticamente constante en todos los casos, por lo que es posible 78 afirmar que este parámetro es el que menor influencia imparte sobre este tipo de resultados. • A más altas temperaturas del líquido refrigerante, el factor Kt va a ser menor en placas con entallas triangulares, rectangulares y semicirculares. Para placas con entalla circular, el factor Kt se mantiene prácticamente invariable. • Placas con concentrador de esfuerzos de tipo circular presentan una marcada línea de soldadura en todo el rango de procesamiento evaluado, lo cual es causante de que el efecto de las condiciones de operación sobre el factor Kt no sea apreciable. • A pesar de no tomar en consideración la influencia que presentan las condiciones de operación entre si, el modelo de ecuación constitutiva desarrollado tiene un alto grado de validez, ya que a excepción de los casos en los que se varía la geometría de las entallas para placas con concentradores semicirculares y circulares, los errores promedios entre los valores teóricos y los obtenidos de las simulaciones siempre son menores al 10%. 6.2 RECOMENDACIONES • Con la finalidad de reafirmar la veracidad de los resultados obtenidos mediante simulaciones, es necesario llevar a cabo pruebas experimentales y ensayos mecánicos bajo condiciones iguales a las utilizadas durante este trabajo. • Estudiar el efecto que presenta el método de elaboración de postizos en pruebas realizadas a placas reales, esto mediante la ejecución de ensayos mecánicos sobre placas manufacturadas mediante la disposición de postizos mecanizados o previamente inyectados. • Calcular el factor Kt mediante la metodología establecida durante este trabajo, de placas elaboradas a partir de distintos materiales termoplásticos y termoestables, con la finalidad de ampliar el espectro de curvas y datos necesarios para ser empleados en el diseño de piezas plásticas. 79 • Llevar a cabo los pasos de mallado de las piezas y simulación de procesos, en un software más actualizado como lo es el Moldex3D, de manera de optimizar el tiempo requerido y disminuir las posibles fuentes de errores. De acuerdo a esto, se recomienda la compra de este programa. • Se debe realizar un análisis de placas con concentradores de esfuerzos triangulares de mayores relaciones r/d que las estudiadas durante este trabajo, con el propósito de verificar la mantenencia del comportamiento presentado en los casos de estudio, ya que la mayor relación r/d empleada fue de 0,47. • Realizar simulaciones en placas con entallas circulares de diámetros mayores a los empleados, con el objetivo de verificar si la tendencia expuesta continúa presente o por el contrario a mayores diámetros de entalla, comienzan a incrementarse nuevamente los esfuerzos generados en las piezas. • Evaluar y comparar todas las formas de entallas estudiadas en esta investigación, partiendo de relaciones geométricas similares. • Elaborar nuevas simulaciones para el estudio del efecto de las condiciones de operación, utilizando un rango más amplio de velocidades de inyección. • Hacer las curvas de Kt para metales con los mismos concentradores utilizados en este caso, de manera que se pueda tener un mayor punto de comparación y así poder establecer concretamente las diferencias entre ellos. • Realizar un modelo de ecuación constitutiva para el cálculo del factor Kt, que tome en consideración el efecto que las condiciones de operación presentan entre si. • Incluir la relación geométrica r/d a la ecuación constitutiva, de manera que se puedan obtener resultados más precisos sin importar las dimensiones que presenten las entallas en las placas. 80 • Desarrollar una ecuación constitutiva basada en el modelo aditivo y comparar con los resultados obtenidos durante esta investigación. • Simular procesos de inyección con placas entalladas en donde sean variados otros parámetros de operación adicionales. Por ejemplo, la presión de inyección. CAPÍTULO VII REFERENCIAS BIBLIOGRAFICAS [1] Malloy, R., “Plastic Part Design for Injection Molding”, Hanser/Gardner Publications, Inc., USA (1994). [2] Ram, A., “Fundamentals of Polymer Engineering”, Plenum Press, USA (1997). [3] Osswald, T., “Polymer Processing Fundamentals”, Hanser/Gardner Publications, Inc., USA (1998). [4] Tadmor, Z., Gogos, C., “Principles of Polymer Processing”, John Wiley & Sons, Inc., USA (1979). [5] Holmes, W., “Polymer Conversion”, Applied Science Publishers Ltd., Londres (1975). [6] “Diseño de Moldes de Inyección de Termoplásticos”, Universidad de Antioquia. Disponible en: http://docencia.udea.edu.co/ingenieria/moldes_inyeccion/unidad_2/maquina.html. Consulta: [Mayo, 2007]. [7] Candal, M. V., Rojas, H. y Jiménez, J., “Effect of the injection molding process conditions over the determination of Kt curves for plastic parts”, Polymer Plastics Technology and Engineering. A publicar (2007). [8] Rao, N. y O´Brien, K., “Design Data for Plastics Engineers”, Hanser/Gardner Publications, Inc., USA (1998). [9] “Manual de Inyección de Plásticos”. Disponible http://www.mailxmail.com/curso/vida/inyecciondeplasticos/capitulo5.htm. en: Consulta: [Junio, 2007]. [10] Wenskus, J., “¿Cómo establecer la ventana de procesamiento? MAD, un método sencillo y económico”, Plástico (Julio-2005). Disponible en: www.plastico.com/tp/secciones/TP/ES/MAIN/IN/ARTICULOS/doc_41536_HTML.html?id Documento=41536. Consulta: [Junio, 2007]. [11] Palza, H., “Introducción a las Propiedades Mecánicas de Polímeros”, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile. Disponible en: http://cabierta.uchile.cl/revista/25/articulos/pdf/edu4.pdf. Consulta: [Mayo, 2007]. [12] Pontífica Universidad Católica de Chile, Escuela de Ingeniería. Disponible en: http://www2.ing.puc.cl/~icm2312/apuntes/materiales/figura7.gif. [Mayo, 2007]. Consulta: 82 [13] Hibbeler, R. C., “Mecánica de Materiales”, Prentice Hall, Inc., Tercera Edición, México (1997). [14] Gere, J., “Mecánica de Materiales”, Internacional Thomson Editores, Quinta Edición, México (2002). [15] Fitzgerald, R., “Mechanics of Materials”, Addison-Wesley Publishing Company, Segunda Edición, USA (1982). [16] Morales, R., Villarroel, S. y Garmendia, D., “Plastic piece stress analysis using simulation software”, SPE’s ANTEC Proceeding (2000), p. 900. [17] Roark, R. y Young, W., “Formulas for Stress and Strain”, McGraw-Hill Book Company, Quinta Edición, USA (1975). [18] Morales, R., Marín, A., Carao, J. y Alvizu, A., “CD Case Design using a Simulation Software for Injection Molding Processing”, SPE´s ANTEC Proceedings (2001), s/p. [19] Candal, M. V., Morales, R. y González, O., “Aplicación de herramientas CAE para la evaluación mecánica de estuches para discos compactos”, Revista de la Facultad de Ingeniería de la Universidad Central de Venezuela (2004). [20] Dieter, G., “Mechanical Metallurgy”, McGraw-Hill Publishing Company, Tercera Edición, USA (1986). [21] Polakowski, N. H. y Ripling, E. J., “Strength and Structure of Engineering Materials”, Prentice Hall, Inc., USA (1966). [22] González, D., “Determinación del Factor de Concentración de Esfuerzos en una Placa con Múltiples Concentradores de Esfuerzo Mediante Algor”, Tesis de Pregrado, Departamento de Ingeniería Mecánica, Universidad de las Américas, Puebla, México (2003). Disponible en: http://catarina.udlap.mx/u_dl_a/tales/documentos/lim/gonzalez_d_e/portada.html. Consulta: [Mayo, 2007]. [23] Budynas, R., “Advanced Strength and Applied stress Analysis”, Irwin McGraw-Hill, USA (1977). [24] Popov, E. P., “Mechanics of materials”, Prentice Hall, Inc., Segunda Edición, USA (1976). [25] Rojas, O. y Rojas, L., “Diseño asistido por computador”, Industrial Data (2006). Disponible en: http://www.scielo.org.pe/pdf/id/v9n1/a02v9n1.pdf. Consulta: [Mayo, 2007]. [26] Sánchez, M., Gordillo, A. Y Martínez, A., “Diseño Optimizado de Piezas de Plásticos”, Plásticos Universales, (Febrero-Marzo 1997). Disponible en: 83 http://www.plastunivers.com/Tecnica/Hemeroteca/ArticuloCompleto.asp?ID=4808. Consulta: [Mayo, 2007]. [27] Gordillo, A., Sánchez, M. Y Martínez A., “Simulación del Proceso de Inyección en el Diseño de Piezas de Plástico”, Plásticos Universales, (Abril-Mayo 1997). Disponible en: http://www.plastunivers.com/Tecnica/Hemeroteca/ArticuloCompleto.asp?ID=5035. Consulta: [Mayo, 2007]. [28] León, H. B., Morales, R. A. y González, A., “Design of an injection mold using C-Mold software”, SPE’s ANTEC Proceeding (2000), s/p. [29] Tassi, P. A. y Engelberger, C. R., “Introducción al Método de Diferencias Finitas”. Disponible en: http://elasticidad.esmartstudent.com/diferencias_finitas.pdf. Consulta: [Agosto, 2007]. [30] Hernández, G., “El Método de Diferencias Finitas”. Disponible en: Consulta: http://mmc.igeofcu.unam.mx/cursos/hidrogeologia/NOTAS_MDF-06.pdf. [Agosto, 2007]. [31] Weaver, W. y Johnston, P., “Finite Elements for Structural Analysis”, Prentice-Hall, Inc., USA (1984). [32] Lo, Y. W., Reible, D. D., Collier, J. y Chen, C. H., Polym. Eng. Sci., 43, 1393 (1994). [33] Young, W. B., Polym. Composites, 15, 118 (1994). [34] Rajupalem, V., Talwar, K. y Friedl C., 670, ANTEC 1997, Toronto (1997). [35] Hetu, J. F., Gao, D. M., Gracia-Rejon, A. y Salloum, G., Polym. Eng. Sci., 38, 223 (1998). [36] Ross, C. T. F., “Finite Element Methods in Engineering Science”, Ellis Horwood Limited, Inglaterra (1990). [37] Vivancos, J., Fenollosa, F. y Costa, L., “Tendencias actuales de los sistemas CAD/CAE/CAM”, Universidad Politécnica de Cataluña. Disponible en: http://www.teleworkspain.com/Art019.htm. Consulta: [Mayo, 2007]. [38] Rojas, O. y Salas, J., “Producción automatizada sistemas CAD/CAE/CAM”, Industrial Data (1999). Disponible en: http://sisbib.unmsm.edu.pe/bibvirtual/Publicaciones/indata/v02_n1/produccion.htm. Consulta: [Mayo, 2007]. [39] “Incorporación de nuevos sistemas CAD/CAM/CAE”, UTecNoticias, N° 16 (Marzo 2004). Disponible en: http://www.frbb.utn.edu.ar/utec/16/n04.html. Consulta: [Mayo, 2007]. [40] Rosato, D. V. y Rosato, M. G., “Injection Molding Handbook”, Kluwer Academic Publishers, Tercera Edición, USA (2000). 84 [41] “Introducción al CAD/CAM”. Disponible en: http://www3.uji.es/~jperis/dfao/apuntes/tema1.pdf. Consulta: [Junio, 2007]. [42] “Soluciones CAD superiores para proyectos grandes y pequeños”. Disponible en: http://www.ptc.com/appserver/mkt/products/home.jsp?k=403. Consulta: [Mayo, 2007]. [43] “Pro-Engineer Overview”. Disponible en: http://www.ptc.com. Consulta: [Mayo, 2007]. [44] Kalnin, F. y Zluhan, G., “Injection mold’s problems solved by CAE analysis”, SPE’s ANTEC Proceeding (1999), s/p. [45] C-Mold Injection/Compression User´s Guide, Ithaca, New York, USA. Disponible en: http://www.dc.engr.scu.edu/cmdoc/IC_doc/IC00_title_TOC.html. Consulta: [Mayo, 2007]. [46] Candal, M. V., Morales, R. y Gorrin, K., “Influence of the Elements Number of a Mesh Over the Simulations Results”, Journal of Plastics Technology. A publicar (2007). [47] Peterson, R., “Stress Concentration Design Factors: Charts and Relations Useful in Making Strength Calculations for Machine Parts and Structural Elements”, John Wiley & Sons, USA (1953). [48] Candal, M. V., Morales, R., D´Armas, H. y Rojas, H., “Stress Concentration Evaluation in an Injected Commercial Piece using Computational Tools”, SPE’s ANTEC Proceeding (2005), p. 3384. [49] Jiménez, J., “Influencia de los Concentradores de Esfuerzos sobre las Propiedades Mecánicas de Placas Plásticas”, Tesis de Pregrado, Universidad Simón Bolívar, Venezuela (2006). [50] Candal, M. V., Rojas, H. y Jiménez, J., “Determination of Kt Curves for Plastic Parts with a Triangular Stress Concentrators”, Polymer Plastics Technology and Engineering. A publicar (2007). [51] Candal, M. V., Rojas, H. y Jiménez, J., “Influence of the Triangular Stress Concentrator on the Mechanical Properties of Plastics Parts”, SPE’s ANTEC Proceeding (2007), p. 615. [52] Spoormaker, J. L. y Heidweiller, A. H., “Failures due to stress concentrations”, SPE’s ANTEC Proceeding (2002), s/p. [53] Heidweiller, A. J. y Van Der Zwet, M. J., “Load-Carrying Ability of Injection Molded Products with Holes”, SPE’s ANTEC Proceeding (2000), s/p. [54] Brostow, W. y Corneliussen, R. D., “Failure of Plastics”, Macmillan Pub., USA (1986). [55] G´Sell, C. y Jonas, J. J., “Determination of the plastic behavior of solid polymers at constant true strain rate”, J. Mater. Sci., 14, 583 (1979). 85 [56] Johnson, G. R. y Cook, W. H., Proc. 7th Int. Symp. on Ballistics, Hague, Holanda (1983). [57] Brooks, J. W., “Processing Wrought Nickel and Titanium Superalloy”, Thermomechanical Processing: Theory, Modeling and Practice. A conference organized in celebration of the 75th anniversary of the Swedish Society for Material Technology (1996). [58] Trejo, M. y Villablanca, V., “Efecto de las Variables de Inyección en las Dimensiones y Propiedades mecánicas de Probetas de PP”, Tesis de Pregrado, Universidad Simón Bolívar, Venezuela (2005). [59] “Método de los Elementos Finitos Para Análisis Estructural”, Criterios de Convergencia, Campus Tecnológico de la Universidad de Navarra. Disponible www.tecnun.es/asignaturas/Estructuras2/Criterios%20convergencia.pdf. en: Consulta: [Mayo, 2007]. [60] Duan, Y., Sargal, A. y Greif, R., “A Uniform Phenomenological Constitutive Model for Glassy and Semicrystalline Polymers”, Polym. Eng. Sci., 41, 1322 (2001). [61] Duffo, P., Monasse, B., Haudin, J., G´Sell, C. y Dahoun, A., “Rheology of polypropylene in the solid state”, J. Mater. Sci., 30, 701 (1995). [62] Tshai, K. Y., Harkin-Jones, E. M. A., Martin, P. J. y Menary, G., “A Unified Approach of Modeling Polypropylene for Thin-Gauge Solid-Phase Thermoforming Applications”, SPE’s ANTEC Proceeding (2004), p. 919. [63] Moldex3D-Mesh. Disponible en: http://www.moldex3d.com/en/products/p04.php. Consulta: [Agosto, 2007]. [64] Reddy, J., “An Introduction to the Finite Element Method”, Segunda Edición, McGrawHill (1993). [65] Candal, M. V., “Diseño y Evaluación de un Nuevo Estuche de CD Utilizando Herramientas de CAD/CAE/CAM”, Tesis de Maestría, Coordinación de Ingeniería Mecánica, Universidad Simón Bolívar (2001). [66] Candal, M. V., Morales, R. y González, O., “Effect of the Finite Element Meshing for Designing Plastic Pieces”, Polymer-Plastics Technology and Engineering, 44, 1573 (2005). [67] Pantani, R. y Titomanlio, G., “Description of PVT Behavior of an Industrial Polypropylene–EPR Copolymer in Process Conditions”, Journal of Applied Polymer Science, 81, 267 (2001). [68] Zuidema, H., Peters, G. W y Meijer, H. E., “Influence of Cooling Rate on PVT-Data of Semicrystalline Polymers”, Journal of Applied Polymer Science, 82, 1170 (2001). 86 [69] Young, R. J. y Lovell, P. A., “Introduction to Polymers”, Segunda Edición, Chapman and Hall, Londres (1991). [70] Ward, I. M. y Sweeney, J., “An Introduction to the Mechanical Properties of Solid polymers”, John Wiley & Sons, Ltd., Segunda Edición, Inglaterra (2004). [71] Chen, S. C., Jong, W. R., Chang, Y. P., Kang, Y., Peng, H. S., Huang, L. T. y Yang, L. K., “Structure Performance of Thin-Wall Injection Molded Parts”, SPE’s ANTEC Proceeding (2001), s/p. [72] Bikales, N., “Mechanical Properties of Polymers”, in “Encyclopedia of Polymers Science and Technology, Vol 8, Wiley-Interscience, USA (1971). [73] Brydson, J. A., “Materiales Plásticos”, Editorial Gráficas Herrera, Tercera Edición, España (1977). [74] Timm, M. W y Couts, M. J., “Relationship of Predicted Shear Stress to Molded Plastic Parts”, SPE’s ANTEC Proceeding (2003), p. 3373. [75] Beaumont, J. P., Nagel, R. y Sherman, R., “Successful Injection Molding. Process, Design and Simulation”, Hanser Gardner Publications, Inc., USA (2002). [76] Pantani, R., Coccorullo, I., Speranza, V. y Titomanlio, G., “Morphology evolution during injection molding: Effect of packing pressure”, Polymer, 48, 2778 (2007). [77] Chen, X. y Gao, F. “A study of packing profile on injection molded part quality”, Materials Science and Engineering, A358, 205 (2003). [78] Morales, R. A., Villarroel, S. y Candal, M. V., ” Effect of Process Variable on the Cavity Pressure in Injection Molding”, Polymer Processing Society (2003). [79] Coxe, M., Barry, C., Bank, D. y Nichols, K., “The Establishment of a Processing Window for Thin Wall Injection Molding of Syndiotactic Polystyrene”, VII International Research/Expert Conference Trends in the Development of Machinery and Associated Technology TMT 2003. Lloret de Mar, Barcelona, España. [80] Viana, J. C., “Development of the skin layer in injection moulding: phenomenological model”, Polymer, 45, 993 (2004). [81] Velarde, D. y Yeagley, M., “Linear Shrinkage Differences in Injection Molded Parts”, SPE’s ANTEC Proceeding (2000), p. 60. [82] G´Sell, C., Rev. Phys. Appl., 23, 1085 (1988). [83] G´Sell, C., Aly-Helal, N. A., Semiatin, S. L. y Jonas, J. J., Polymer, 33, 1244 (1992). [84] Andrews, J. M. y Ward, I. M., J. Mater. Sci., 5, 411 (1970). [85] G´Sell, C., Aly-Helal, N. A. y Jonas, J. J., J. Mater. Sci., 18, 1731 (1983). [86] Chang, R., “Química”, McGraw-Hill, Séptima Edición, USA (2002). 87 [87] Cantal, M. V., Morales, R. y Villaroel, S., “C-MOLD, Guía del estudiante y ejercicios guiados”, Departamento de Mecánica, Universidad Simón Bolívar, Venezuela (2001). APÉNDICES APÉNDICE A: Planos del molde y las placas con entallas Figura A.1 Placa portacavidades del molde [87]. APÉNDICE B: Gráficas elaboradas para el estudio del criterio de la convergencia 0 10 20 30 40 50 60 70 80 90 Temperatura de desmoldeo (ºC) Fuerza de cierre (Ton) 140 120 100 80 60 40 20 0 50 40 30 20 10 0 0 10 35 30 25 20 15 10 5 0 0 10 20 30 40 50 60 70 80 90 Temperatura del refrigerante (ºC) Número de Reynolds 1,2E+04 1,0E+04 8,0E+03 6,0E+03 4,0E+03 2,0E+03 0,0E+00 20 10 0 40 50 60 70 Nº de nodos en la entalla 80 90 Temperatura de la masa al final del llenado (ºC) Temperatura de la pared del molde (ºC) 30 30 80 90 80 90 3 2 1 0 0 10 20 30 40 50 60 70 40 35 30 25 20 15 10 5 0 10 20 30 40 50 60 70 80 90 80 90 Nº de nodos en la entalla 40 20 70 4 0 50 60 70 80 90 50 10 60 5 Nº de nodos en la entalla 0 50 Nº de nodos en la entalla 1,4E+04 10 20 30 40 40 6 Nº de nodos en la entalla 0 30 Nº de nodos en la entalla Máximo esfuerzo de corte en procesamiento (MPa) Máximo esfuerzo de corte en cargas de servicio (MPa) Nº de nodos en la entalla 20 300 250 200 150 100 50 0 0 10 20 30 40 50 60 70 Nº de nodos en la entalla Figura B.1 Resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos semicirculares. 100 80 60 40 20 0 0 10 20 30 40 50 60 70 80 90 Porcentaje de rechupe (%) Porcentaje total en peso (%) 120 2,5 2 1,5 1 0,5 0 0 10 20 80 70 60 50 40 30 20 10 0 0 10 20 30 40 50 60 70 80 90 3 2 1 0 40 50 60 70 80 90 Desplazamiento en X (mm) Contracción volumétrica (%) 4 20 30 0,20 0,15 0,10 0,05 0,00 30 40 50 60 70 Nº de nodos en la entalla 80 90 Desplazamiento en Z (mm) Desplazamiento en Y (mm) 0,25 20 80 90 0,3 0,2 0,1 0 0 10 20 30 40 50 60 70 80 90 0,30 0,25 0,20 0,15 0,10 0,05 0,00 0 10 20 30 40 50 60 70 80 90 80 90 Nº de nodos en la entalla 0,30 10 70 0,4 Nº de nodos en la entalla 0 60 Nº de nodos en la entalla 5 10 50 0,5 Nº de nodos en la entalla 0 40 Nº de nodos en la entalla Diferencia de temperatura (ºC) Presión al final del llenado (MPa) Nº de nodos en la entalla 30 0,07 0,06 0,05 0,04 0,03 0,02 0,01 0 0 10 20 30 40 50 60 70 Nº de nodos en la entalla Figura B.2 Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos semicirculares. APÉNDICE C: Relaciones geométricas, condiciones de operación, esfuerzos y Kt obtenidos en las placas estudiadas Tabla C.1 Relaciones geométricas, condiciones de operación y esfuerzos obtenidos para el cálculo de Kt en placas con entallas triangulares. Placa 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 D d h R d/D (mm) (mm) (mm) (mm) 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 71,50 65,50 59,50 53,50 47,50 41,50 35,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 7,00 10,00 13,00 16,00 19,00 22,00 25,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 10,00 13,00 19,00 22,00 25,00 28,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 19,00 0,84 0,77 0,70 0,63 0,56 0,49 0,42 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 r/d 0,22 0,24 0,27 0,30 0,34 0,39 0,45 0,17 0,22 0,32 0,37 0,42 0,47 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 Tfundido Psostenida Vinyección (°C) (Mpa) (cm/s) 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 190,00 210,00 230,00 250,00 270,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,00 6,00 7,00 8,00 9,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 4,50 5,50 6,50 7,50 8,50 5,50 5,50 5,50 Trefrigerante σ servicio σ proceso (°C) (MPa) (MPa) 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 25,00 35,00 48,00 20,02 21,12 21,67 20,58 21,99 19,47 22,01 21,73 21,90 22,07 19,02 19,95 19,48 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 21,81 11,72 12,22 12,29 12,44 12,15 11,93 11,69 12,51 12,28 12,29 11,52 11,76 11,84 8,07 10,36 12,10 13,24 15,26 15,31 16,88 12,10 9,98 8,38 11,87 12,10 12,19 12,23 12,39 15,15 12,10 9,66 (σs2 + σp2)1/2 23,20 24,40 24,91 24,05 25,12 22,83 24,92 25,07 25,11 25,26 22,24 23,16 22,80 23,26 24,15 24,94 25,51 26,62 26,65 27,58 24,94 23,98 23,36 24,83 24,94 24,99 25,00 25,08 26,56 24,94 23,85 σ placa sin entalla (MPa) 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 10,53 12,40 14,18 16,37 18,28 15,85 17,70 14,18 12,15 11,02 14,26 14,18 14,08 13,99 14,00 16,49 14,18 12,03 Kt simul Kt teo Error (%) 0,609 0,579 0,567 0,588 0,563 0,619 0,567 0,564 0,563 0,559 0,635 0,610 0,620 0,453 0,513 0,569 0,642 0,687 0,595 0,642 0,569 0,507 0,472 0,574 0,569 0,563 0,560 0,558 0,621 0,569 0,504 0,643 0,625 0,613 0,608 0,609 0,617 0,632 0,613 0,613 0,613 0,613 0,613 0,613 0,482 0,549 0,613 0,676 0,737 0,555 0,596 0,613 0,603 0,561 0,613 0,613 0,613 0,613 0,613 0,558 0,613 0,687 3,401 4,564 4,586 1,966 4,605 0,198 6,458 4,900 5,000 5,400 2,200 0,300 0,700 2,900 3,600 4,400 3,400 5,000 4,000 4,600 4,400 9,600 8,900 3,900 4,400 5,000 5,300 5,500 6,300 4,400 18,300 Tabla C.2 Relaciones geométricas, condiciones de operación y esfuerzos obtenidos para el cálculo de Kt en placas con entallas rectangulares. Placa 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 D d h r d/D (mm) (mm) (mm) (mm) 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 71,50 65,50 59,50 53,50 47,50 41,50 35,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 59,50 7,00 10,00 13,00 16,00 19,00 22,00 25,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 13,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 10,00 13,00 19,00 22,00 25,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 28,00 0,84 0,77 0,70 0,63 0,56 0,49 0,42 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 r/d 0,22 0,24 0,27 0,30 0,34 0,39 0,45 0,17 0,22 0,32 0,37 0,42 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 0,47 Tfundido Psostenida Vinyección (°C) (Mpa) (cm/s) 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 190,00 210,00 230,00 250,00 270,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,00 6,00 7,00 8,00 9,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 4,50 5,50 6,50 7,50 8,50 5,50 5,50 5,50 Trefrigerante σ servicio σ proceso (°C) (MPa) (MPa) 35,00 35,00 35,00 35,00 35,00 35,00, 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 25,00 35,00 48,00 20,24 23,45 20,29 21,69 21,70 21,80 19,61 20,43 21,17 21,11 22,23 23,36 24,15 22,56 23,87 22,83 23,18 23,08 23,12 23,18 22,83 22,76 22,64 23,62 22,83 22,85 22,97 22,80 22,92 22,83 22,90 12,75 12,81 11,89 12,15 11,81 11,28 11,58 11,55 11,89 12,45 12,85 12,64 13,19 7,62 10,60 12,67 15,48 17,96 11,87 15,65 12,67 10,09 8,56 12,77 12,67 12,60 12,54 12,48 16,57 12,67 10,00 (σs2 + σp2)1/2 23,92 26,72 23,52 24,86 24,71 24,55 22,77 23,47 24,28 24,51 25,68 26,56 27,52 23,81 26,12 26,11 27,87 29,24 25,99 27,97 26,11 24,90 24,20 26,85 26,11 26,09 26,17 25,99 28,28 26,11 24,99 σ placa sin entalla (MPa) 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 10,53 12,40 14,18 16,37 18,28 15,85 17,70 14,18 12,15 11,02 14,26 14,18 14,08 13,99 14,00 16,49 14,18 12,03 Kt simul Kt teo Error (%) 0,591 0,529 0,601 0,568 0,572 0,576 0,621 0,602 0,582 0,576 0,550 0,532 0,513 0,442 0,475 0,543 0,587 0,625 0,610 0,633 0,543 0,488 0,455 0,531 0,543 0,540 0,535 0,539 0,583 0,543 0,481 0,562 0,552 0,549 0,551 0,560 0,575 0,597 0,549 0,549 0,549 0,549 0,549 0,549 0,447 0,499 0,549 0,597 0,642 0,519 0,542 0,549 0,537 0,504 0,549 0,549 0,549 0,549 0,549 0,503 0,549 0,610 2,881 2,332 5,229 1,664 1,174 0,058 2,416 5,300 3,300 2,700 0,100 1,700 3,600 0,500 2,400 0,600 1,000 1,700 9,100 9,100 0,600 4,900 4,900 1,800 0,600 0,900 1,400 1,000 8,000 0,600 12,900 Tabla C.3 Relaciones geométricas, condiciones de operación y esfuerzos obtenidos para el cálculo de Kt en placas con entallas semicirculares. Placa 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 D d h r d/D (mm) (mm) (mm) (mm) 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 78,50 75,50 72,50 69,50 66,50 63,50 60,50 57,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 69,50 3,50 5,00 6,50 8,00 9,50 11,00 12,50 14,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 8,00 7,00 10,00 13,00 16,00 19,00 22,00 25,00 28,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 16,00 0,92 0,88 0,85 0,81 0,78 0,74 0,71 0,67 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 0,81 r/d 0,09 0,13 0,18 0,23 0,29 0,35 0,41 0,49 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 0,23 Tfundido Psostenida Vinyección (°C) (Mpa) (cm/s) 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 190,00 210,00 230,00 250,00 270,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,00 6,00 7,00 8,00 9,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 4,50 5,50 6,50 7,50 8,50 5,50 5,50 5,50 Trefrigerante σ servicio σ proceso (°C) (MPa) (MPa) 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 25,00 35,00 48,00 18,74 18,15 16,45 17,25 16,63 15,23 15,33 14,93 17,37 17,37 17,37 17,37 17,37 17,37 17,37 17,37 17,37 17,37 15,67 15,64 15,67 15,67 15,67 17,37 17,37 17,37 12,06 12,17 12,11 12,16 12,18 12,16 12,08 12,02 8,02 10,42 12,44 14,65 16,97 14,77 17,15 12,44 10,12 8,52 12,53 12,54 12,36 12,29 12,27 15,52 12,44 9,82 (σs2 + σp2)1/2 13,06 13,16 13,10 13,15 13,17 13,15 13,07 13,02 19,13 20,26 21,37 22,72 24,28 22,80 24,41 21,37 20,10 19,35 20,06 20,05 19,96 19,91 19,90 23,29 21,37 19,95 σ placa sin entalla (MPa) 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 10,53 12,40 14,18 16,37 18,28 15,85 17,70 14,18 12,15 11,02 14,26 14,18 14,08 13,99 14,00 16,49 14,18 12,03 Kt simul Kt teo Error (%) 1,082 1,074 1,079 1,075 1,073 1,075 1,081 1,085 0,550 0,612 0,664 0,721 0,753 0,695 0,725 0,664 0,604 0,570 0,711 0,707 0,705 0,703 0,704 0,708 0,664 0,603 0,758 0,755 0,754 0,753 0,753 0,755 0,757 0,760 0,619 0,691 0,753 0,807 0,851 0,688 0,730 0,753 0,754 0,729 0,753 0,753 0,753 0,753 0,753 0,700 0,753 0,822 32,398 31,865 32,533 32,200 31,967 32,034 32,400 32,467 6,900 7,900 8,900 8,600 9,800 0,700 0,500 8,900 15,000 15,900 4,200 4,600 4,800 5,000 4,900 0,800 8,900 21,900 Tabla C.4 Relaciones geométricas, condiciones de operación y esfuerzos obtenidos para el cálculo de Kt en placas con entallas circulares. Placa 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 D d (mm) (mm) Tfundido Psostenida Vinyección Trefrigerante σ servicio (°C) (Mpa) (cm/s) (°C) (MPa) σ proceso d/D 78,50 75,50 72,50 69,50 66,50 63,50 60,50 57,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 78,50 0,92 0,88 0,85 0,81 0,78 0,74 0,71 0,67 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 0,92 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 190,00 210,00 230,00 250,00 270,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 230,00 12,61 12,64 12,59 12,61 12,62 12,64 12,65 12,68 8,06 10,57 12,70 15,17 17,36 14,05 16,60 12,70 10,19 8,69 12,46 12,44 12,42 12,38 12,32 15,79 12,70 9,99 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 85,50 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,00 6,00 7,00 8,00 9,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 7,00 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 5,50 4,50 5,50 6,50 7,50 8,50 5,50 5,50 5,50 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 35,00 25,00 35,00 48,00 21,01 19,32 18,37 18,09 18,73 18,22 18,08 17,79 6,39 6,39 6,39 6,39 6,39 6,39 6,39 6,39 6,38 6,39 6,12 6,12 6,12 6,12 6,12 6,39 6,39 6,39 (MPa) (σs2 + σp2)1/2 24,50 23,09 22,27 22,05 22,58 22,18 22,07 21,85 10,29 12,35 14,22 16,46 18,50 15,43 17,79 14,22 12,02 10,79 13,88 13,86 13,85 13,81 13,76 17,03 14,22 11,86 σ placa sin entalla (MPa) 14,13 14,13 14,13 14,13 14,13 14,13 14,13 14,13 10,53 12,40 14,18 16,37 18,28 15,85 17,70 14,18 12,15 11,02 14,26 14,18 14,08 13,99 14,00 16,49 14,18 12,03 Kt simul Kt teo Error (%) 0,577 0,612 0,634 0,641 0,626 0,637 0,640 0,647 1,023 1,004 0,997 0,995 0,988 1,027 0,995 0,997 1,011 1,021 1,027 1,023 1,017 1,013 1,017 0,968 0,997 1,014 1,000 1,032 1,058 1,077 1,090 1,096 1,096 1,089 1,024 1,010 1,000 0,994 0,992 1,015 1,005 1,000 1,000 1,005 1,000 1,000 1,000 1,000 1,000 1,021 1,000 0,975 42,293 41,999 42,360 43,577 46,350 45,878 45,562 44,202 0,100 0,600 0,300 0,100 0,400 1,200 1,000 0,300 1,100 1,600 2,700 2,300 1,700 1,300 1,700 5,300 0,300 3,900 APÉNDICE D: Cálculo de Kt teórico, simulado y error porcentual De acuerdo a lo descrito en el capítulo IV, el factor de concentración de esfuerzos Kt fue calculando mediante el empleo de la siguiente ecuación: Kt = σ max σ nom (ecuación 1) en donde σmax corresponde al esfuerzo de Mises-Hencky resultante, calculado a partir de los esfuerzos en cargas de servicio y procesamiento mediante la ecuación 5.1 para una placa sin entalla, a la vez de que σnom es el esfuerzo de Mises-Hencky resultante para las distintas placas entalladas. A partir de los valores reportados para los esfuerzos y que son presentados en las tablas del Apéndice C, fue obtenido el factor Kt. Ejemplo: Para la placa N° 1 con entalla de tipo triangular y relaciones geométricas d/D= 0,84 y r/d= 0,22 se tiene lo siguiente: σmax = 14, 13 MPa σnom = 23,20 MPa Kt = 14,13MPa = 0,609 23,20 MPa De igual manera, el cálculo del factor de concentración de esfuerzos teórico se llevó a cabo a través de la utilización de la ecuación 5.6, la cual luego de sustituir los valores para cada una de las constantes presentadas en la tabla 5.3 tiene la siguiente forma: [ ][ ] Kt = 10,428*(0,84) −12,626*(0,84) +13,295* − 2,00E − 03*(7MPa) + 0,126*(7MPa) + 0,193 [ 2 2 ] −866,38 308,15° K * − 3,00E − 04* (503,15°K ) + 0,254* (503,15°K ) − 53,318 * exp 2 −863,99 503,15° K * exp = 0,643 Finalmente, el error porcentual fue obtenido a partir de los valores para el Kt anteriormente calculados y mediante el uso de la expresión mostrada a continuación: Error = ( Kt exp erimental − Kt teórico ) 2 * 100 (ecuación 2) en donde al sustituir los valores correspondientes se obtiene el siguiente resultado: Error = (0,609 − 0,643) 2 * 100 = 3,396% APÉNDICE E: Gráficas de Kt con respecto a los parámetros geométricos d/D y r/d para placas metálicas con entallas tipo “U” Figura E.1 Kt en función de d/D para barras metálicas sometidas a tracción con concentradores de esfuerzos tipo “U” (r/d de 0,001 a 0,05) [47]. Figura E.2 Kt en función de r/d para barras metálicas sometidas a tracción con concentradores de esfuerzos tipo “U” (r/d de 0 a 0,3) [47]. Figura E.3 Kt en función de r/d para barras metálicas sometidas a tracción con concentradores de esfuerzos tipo “U” (r/d de 0,3 a 100) [47].