Extrapolacion de Tafel

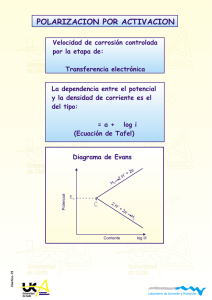
TÉCNICAS ELECTROQUÍMICAS DE CORRIENTE DIRECTA PARA LA
DETERMINACIÓN DE LA VELOCIDAD DE CORROSION
TÉCNICA DE EXTRAPOLACIÓN DE TAFEL O DE INTERSECCIÓN
J. Genescá. Dpto. Ingeniería Metalúrgica. Facultad Química. UNAM. Ciudad
Universitaria. 04510 México D.F. genesca@servidor.unam.mx
COEFICIENTES DE TAFEL
Si la concentración de los reactivos y de los productos es uniforme en el electrolito, la
ecuación de Butler-Volmer toma la forma
η
j = j 0 exp a
 βa

η
 − j 0 exp  c

 βc



Donde β a y β c, son los coeficientes de Tafel anódico y catódico respectivamente:
βa =
RT
αnF
βc =
RT
(1 − α ) nF
Esta ecuación se aplica a las reacciones electródicas en las cuales la velocidad está
controlada por el proceso de transferencia de carga en la interfase electrodo/electrolito.
Esta situación se conoce a menudo como control por activación o control activacional y
el sobrepotencial correspondiente como sobrepotencial de activación, ηA.
El valor de los coeficientes de Tafel , β a y β c, depende del mecanismo de las reacciones
que tiene lugar en los electrodos, los cuales comprenden muy a menudo varias etapas. Sin
embargo, no es necesario conocer este mecanismo para poder utilizar la ecuación de
Butler-Volmer, ya que ésta describe la cinética del proceso de transferencia de cargas de
una manera global, independientemente del mecanismo, a partir de tres magnitudes
fácilmente medibles: j0 , β a y β c.
Las siguientes fórmulas definen los coeficientes de Tafel anódico y catódico.
βa =
dE
d ln j a
βc = −
dE
d ln j c
RECTAS DE TAFEL
Para determinar experimentalmente los parámetros cinéticos j0 , βa y β c , es recomendable
una representación gráfica en la que la densidad de corriente esté en una escala
logarítmica, ya que así se pone en evidencia la relación lineal existente entre el logj y el
sobrepotencial, η, especialmente cuando este último, en valor absoluto, tiene un valor
grande.
Se denomina región ó dominio de Tafel anódico (zona Tafeliana), aquella región en la
cual el potencial que corresponde a η/β a >> 1. La ecuación se convierte en
η 
j = j a = j 0 exp  a 
 βa 
Tomando logaritmos se obtiene:
η = − β a ln j 0 + β a ln j
Pasando a logaritmos de base diez y definiendo las constantes de Tafel anódicas, aa y ba
se obtiene la ecuación de Tafel de una reacción anódica, también llamada recta de Tafel
anódica:
η = a a + ba log j
a a = −2.303β a ln j 0
ba = 2.303β a
De manera análoga, para el dominio catódico de Tafel, η/βc <<1:
 η
j = jc = − j 0 exp  − c
 βc
η = β c ln j 0 − β c ln j



Lo cual permite expresar las constantes de Tafel catódicas, ac y bc de la ecuación de Tafel
de una reacción catódica:
η = a c − bc log i
a c = 2.303β c ln j 0
bc = 2.303 β c
Las ecuaciones de Tafel describen los límites anódico y catódico de la ecuación de
Butler-Volmer. Su descubrimiento a principios del siglo veinte, en el año de 1904, por
Tafel al estudiar el comportamiento del sobrepotencial para la reacción de
desprendimiento de H2 en función de la densidad de corriente, precedió durante muchos
años a la ecuación de Butler-Volmer.
Cuando se obtiene una curva de polarización experimental, la extrapolación de la recta
que aparece en el dominio Tafeliano al valor del potencial de equilibrio, permite
determinar la densidad de corriente de intercambio, j0 , Figura 1. El inverso del valor de la
pendiente de estas rectas proporciona el valor de los coeficientes de Tafel, β a y β c.
ECUACION DE BUTLER-VOLMER DE UN ELECTRODO MIXTO
La ecuación de Butler-Volmer se puede aplicar a un electrodo mixto, por ejemplo, al caso
concreto de la corrosión del acero en HCl, en ausencia de gradientes de concentración.
Tienen lugar simultáneamente dos reacciones:
Fe → Fe2+ + 2e
reacción anódica
2H+ + 2 e → H2
reacción catódica
Si se toma al acero como electrodo de trabajo en una celda electroquímica y se aplica un
determinado potencial, resulta en una densidad de corriente medible, cuyo valor
corresponde a la suma de las densidades de corriente parciales
j = jFe + jH = ja,Fe + jc,Fe + ja,H +jc,H
Figura 1. Esquema de una reacción anódica en un diagrama de Tafel. E0 a : potencial de
equilibrio, j0 a: densidad corriente intercambio, b: pendiente de Tafel = 2.303β
Los subíndices Fe e H se refieren a las reacciones parciales. Cerca del potencial de
corrosión, Ecorr, la contribución de jc,H y ja,H se puede considerar despreciable. (jc,H ≅ ja,H ≅
0) lo que permite simplificar la ecuación:
j = jFe + jH = ja,Fe +jc,H
En el potencial de corrosión (E = Ecorr), la densidad de corriente j es cero.
j = ja,Fe(Ecorr) +jc,H(Ecorr) = 0
Se ha supuesto por una parte que la transferencia de carga en la interfase metal/solución
constituye la etapa limitante y por otra, que las cinéticas de las dos reacciones parciales
son independientes. La densidad de corriente parcial de cada reacción obedece entonces
a la ecuación de Butler-Volmer.
 η
j Fe = j a , Fe + j c , Fe = j 0 , Fe exp  Fe
 β a , Fe
 η
j H = j a , H + j c , H = j 0 , H exp  H
 β a, H


 − j 0 , Fe exp  − η Fe

 β c , Fe




 − j 0 , H exp  − η H

 β
c ,H










Las mediciones de polarización llevaron al desarrollo, en 1930, de la teoría del potencial
mixto, con el objeto de poder explicar los resultados experimentales obtenidos. La Figura
2a muestra una representación esquemática de una reacción anódica y catódica, típicas de
un proceso de corrosión, así como, Figura 2b, la correspondiente curva de polarización
experimental que se puede derivar de las mismas.
METODOS ELECTROQUIMICOS DE ESTIMACION DE LA VELOCIDAD DE
CORROSION
Cuando toman parte en la reacción especies cargadas, como es el caso de los procesos de
corrosión, la barrera de energía que debe vencerse en la transferencia de carga es afectada
por el campo eléctrico y puede demostrarse, a partir de la teoría de la cinética
electroquímica que las densidades de corriente de los procesos parciales
Me ⇔ Men+ + neO2 + 2 H2O + 4 e- ⇔ 4 OHSe ajustan a las expresiones
 αnFη 
j a = j corr exp 

 RT 
− (1 − α )nFη 
j c = − j corr exp 

RT


Donde T representa la temperatura absoluta, R la constante de los gases perfectos, F la
constante de Faraday, n el número de electrones intercambiados en el proceso redox, α y
(1-α) los coeficientes de transferencia de carga, relacionados con la caída de potencial a
través de la doble capa que rodea el electrodo (normalmente el valor de ambos es
próximo a 1/2), η la polarización (sobrepotencial) aplicada y jcorr la densidad de corriente
de corriente de corrosión buscada, que puede transformarse en pérdida de peso o de
espesor a partir de la segunda ley de Faraday.
El equilibrio eléctrico existente en el potencial de corrosión libre, expresado como:
It = Ia + Ic = 0
Ia = Ic = Icorr
impide la determinación directa de jcorr. Cuando se rompe dicho equilibrio, imponiendo
una polarización al electrodo, se aprecia experimentalmente una corriente externa,
resultante de la suma algebraica de las correspondientes a los procesos parciales:
  αnFη a 
 − (1 − α ) nFη c
j t = j a + j c = j corr  exp 
 − exp 
RT

  RT 



Partiendo de esta ecuación, conocida como de Wagner y Traud (1), se consigue, a través
de dos casos límite, la aproximación de alto campo o alto sobrepotencial (extrapolación
de Tafel o intersección) y la de bajo campo o bajo sobrepotencial (método de resistencia
de polarización), una estimación de jcorr, es decir, de la velocidad de corrosión.
METODO DE EXTRAPOLACIÓN DE TAFEL O DE INTERSECCION
Para polarizaciones suficientemente grandes:
η ≥
RT
α nF
o bien
−η ≥
RT
(1 − α ) nF
la ecuación general de Wagner y Traud se reduce a las ecuaciones de las semireacciones
anódica y catódica que se corresponden con las rectas de Tafel respectivas, con
pendientes
ba =
2.3 RT
αnF
o bien
bc =
− 2.3 RT
(1 − α ) nF
Para comprobarlo basta tomar logaritmos en cualquiera de las citadas ecuaciones, por
ejemplo en la reacción anódica
log j a = log j corr +
de donde:
αnF
η
2.3RT
η=
− 2.3RT
2.3 RT
log j corr +
log j a = a + ba log j a
αnF
αnF
Entonces, para un sistema metal/electrolito dado, jcorr tiene un valor determinado y el
primer término del segundo miembro puede englobarse en la constante a de la ley de
Tafel.
En las proximidades de Ecorr, para polarizaciones pequeñas, los procesos anódicos y
catódicos se influyen mutuamente y las curvas de polarización experimentales se apartan
del curso semilogarítmico previsto por la ley de Tafel. Sin embargo, para η=0 (es decir,
cuando E = Ecorr), de cualquiera de las ecuaciones resulta:
ja = |jc| = jcorr
lo cual permite determinar la jcorr buscada sin mas que extrapolar cualquiera de las rectas
de Tafel obtenidas a polarizaciones grandes hasta el valor E=Ecorr, tal como se
esquematiza en la Figuras 2b y 3a. En la Figura 3a se presenta el diagrama de Tafel para
el proceso de corrosión de un metal en un medio ácido con oxígeno disuelto, mientras
que en la Figura 3b se reproduce el mismo diagrama, pero tomando en consideración lo
que suele ocurrir frecuentemente en los casos reales, cuando el proceso catódico de
reducción del O2 está controlado por difusión. La Figura 4 reproduce un diagrama de
Tafel experimental correspondiente al proceso de corrosión de un acero dulce en una
salmuera.
La principal ventaja y desventaja de este método, derivado en principio por Wagner y
Traud (1) y Evans y Hoar (2), y que tiene una amplia aplicabilidad en la práctica, reside
en la necesidad del trazado completo de las curvas de polarización que por una parte
posibilita un análisis electroquímico de la cinética del proceso de corrosión y, por otra,
puede dar lugar a modificaciones de la superficie del electrodo por efecto de las elevadas
polarizaciones aplicadas. Inversamente, si se llega a una concordancia entre los valores
de las velocidades de corrosión derivadas de los ensayos gravimétricos de pérdidas de
peso y las obtenidas con la utilización de este método, puede concluirse que el proceso de
corrosión se realiza según un mecanismo electroquímico característico.
El cálculo de la velocidad de corrosión por el método de extrapolación de Tafel, conocido
también como método de intersección, se basa en la extrapolación de la zona lineal o de
Tafel en un diagrama experimental E vs. log j. Según este método se puede obtener la jcorr
sin más que extrapolar cualquiera de las rectas de Tafel hasta el valor del Ecorr, tal como
se representa en la Figura 1.
Para un buen desarrollo experimental de esta técnica se recomienda consultar las
siguientes normas ASTM:
•
•
ASTM G 3 - 89. Standard Practice for Conventions Applicable to Electrochemical
Measurements in Corrosion Testing.
ASTM G 5 - 94. Standard Reference Test Method for making Potentiostatic and
Potentiodynamic Anodic polarization Measurements.
•
•
ASTM G 59 - 97. Standard Test Method for Conducting Potentiodynamic
Polarization Resistance Measurements.
ASTM G 102 - 89. Standard Practice for Calculation of Corrosion rates and
Related Information from Electrochemical Measurements.
Figura 3a. Diagrama de Tafel correspondiente a la corrosión de un metal, M, en un
electrolito ácido en presencia de oxígeno disuelto.
En la práctica se acostumbra a la representación gráfica del log I versus E que también se
conoce como diagrama de Tafel. El diagrama de Tafel de la Figura 1 se puede generar
directamente a partir de la ecuación de Butler-Volmer.
En la práctica, muchos sistemas de corrosión están controlados cinéticamente por la
polarización de activación y obedecen por tanto a la ecuación de Butler – Volmer. Si éste
es el caso, la representación gráfica del logaritmo de la corriente respecto al potencial
aplicado debe presentar un comportamiento lineal (Tafeliano) en sentido anódico y
catódico que indica precisamente el control cinético del sistema bajo estudio. Sin
embargo, pueden existir complicaciones, como por ejemplo:
1. Polarización por concentration, cuando la velocidad de la reacción está controlada por
la velocidad a la que llegan las especies reactivas a la superficie metálica. A menudo las
reacciones catódicas presentan una polarización por concentración para altos valores de
corriente, cuando la difusión del O2 o de los iones H+ no es lo suficientemente rápida
como para mantener un control cinético activacional.
2. La formación de óxidos, los cuales pueden llevar o no a la pasivación del metal, pero
alteran la superficie de la muestra metálica ensayada. El estado de la superficie puede
afectar los valores de las constantes de la ecuación. Oxide formation, which may or may
not lead to passivation, can alter the surface of the sample being tested. The original
surface and the altered surface may have different values for the constants in Equation 12.
3. Otros efectos que puedan modificar la superficie, tales como la disolución preferencial
de un componente de una aleación son también causa de problemas.
4. Un control mixto del proceso de corrosión cuando mas de una reacción, anódica o
catódica, pueden ocurrir simultáneamente, puede complicar el modelo. Un ejemplo de
control mixto es la reducción simultánea del O2 y H+.
5. Por último, otra causa de error en el modelo cinético controlado únicamente por
activación necesario para la validez de la ecuación de Tafel es la caída de potencial que
tiene lugar como resultado del paso de la corriente que circula por la celda a través de la
resistencia eléctrica del electrolito de la misma celda. Si este efecto no es muy severo
puede llegar a corregirse (compensarse) con el dispositivo de compensación de IR del
propio potenciostato. Finalmente, las caídas de potencial resultado del paso de una
corriente a través de la resistencia de la solución en la celda produce errores en el modelo
cinético. Este último efecto, si no es muy severo, puede ser corregido mediante la
compensación IR del propio potenciostato.
En muchos casos, las complicaciones como las indicadas anteriormente, pueden ser la
causa de la no-linealidad en las gráficas de Tafel. Todos los resultados derivados de una
gráfica de Tafel que no tenga una bien definida región lineal deben ser utilizados con
mucha precaución..
Como ya se ha indicado anteriormente, el análisis clásico de Tafel se lleva a cabo
mediante la extrapolación de la porción lineal de la curva de polarización (log j vs E),
anódica y/o catódica, al valor del potencial de corrosión, como se muestra en la Figura
2b. El valor tanto de la corriente anódica como de la catódica en la intersección, es decir
la correspondiente al Ecorr, es Icorr . Desafortunadamente, los sistemas de corrosión reales
no presentan, muy a menudo, en sus curvas de polarización, una región lineal lo
suficientemente extensa que permita una extrapolación con garantías. La mayoría de los
equipos modernos disponen de un software adecuado para este tratamiento. Por ejemplo,
el Gamry Instruments' DC105 DC Corrosion Techniques software, puede llevar a cabo un
ajuste numérico de la ecuación de Butler – Volmer. Los valores experimentales se
ajustan a la ecuación de Butler – Volmer, modificando los correspondientes valores del
Ecorr, Icorr , ba, and bc. Este método de ajuste de la curva tiene la ventaja que no requiere
una bien definida porción lineal en la correspondiente curva de polarización.
Figura 3b. Curva de polarización (diagrama de Tafel) correspondiente al proceso de
corrosión del acero en un medio ácido con oxígeno disuelto, estando el proceso catódico
controlado por la difusión del O2 .
After 24 hr, 0 rpm
-0.35
A 25ppm
-0.40
C 25ppm
E (V vs SCE)
-0.45
-0.50
-0.55
-0.60
-0.65
1E-06
1E-05
1E-04
1E-03
1E-02
-2
i (A cm )
Figura 4. Curva de polarización de un acero 1018 en una solución de salmuera con
inhibidor tipo imidazolina (25 ppm) a temperatura ambiente (3).
REFERENCIAS
1. C. Wagner y W. Traud, Z. Elektrochem. 44, 391 (1938).
2. U.R. Evans y T.P. Hoar, Proc. Roy. Soc. A., 137, 343 (1932).
3. J. Mendoza, R. Duran and E. Garcia, Corrosion’2002, Paper # 02491. Houston
(2002).