METODOS DE SOLUCION DE PROBLEMAS DE RAZONAMIENTO
Anuncio

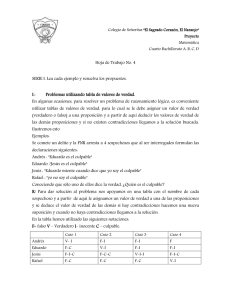
SEGUNDO BIMESTRE SEMANA 14 LÓGICA MATEMÁTICA 4to. Bachillerato en Computación METODOS DE SOLUCION DE PROBLEMAS DE RAZONAMIENTO LOGICO Problemas de razonamiento lógico son los que no dependen tanto del contenido sino del razonamiento lógico (natural, adecuado, correcto), aunque es muy difícil establecer esto debido a que para resolver cualquier problema tenemos que razonar; sí podemos afirmar que existen problemas en los que predomina el razonamiento lógico, siendo el contenido matemático que se necesita muy elemental. Por conveniencia, sin pretender clasificar los mismos, hemos dividido estos problemas didácticamente para que ustedes puedan comprender algunas vías, métodos y procedimientos de cómo enfrentarse a la resolución de problemas de razonamiento lógico, desarrollar su modo de actuación y prepararlos para la vida. PROBLEMAS UTILIZANDO TABLA DE VALORES DE VERDAD En algunas ocasiones, para resolver un problema de razonamiento lógico, es conveniente utilizar tablas de valores de verdad, para lo cual se le debe asignar un valor de verdad (verdadero o falso) a una proposición y a partir de aquí deducir los valores de verdad de las demás proposiciones y si no existen contradicciones llegamos a la solución buscada. Ilustremos esto mediante tres ejemplos: 1) Se comete un delito y la PNR arresta a 4 sospechosos que al ser interrogados formulan las declaraciones siguientes: Andrés : "Eduardo es el culpable" Eduardo :"Jesús es el culpable" Jesús : "Eduardo miente cuando dice que yo soy el culpable" Rafael : "yo no soy el culpable" Conociendo que sólo uno de ellos dice la verdad, ¿Quién es el culpable? R/ Para dar solución al problema nos apoyamos en una tabla con el nombre de cada sospechoso y a partir de aquí le asignamos un valor de verdad a una de las proposiciones y se deduce el valor de verdad de las demás si hay contradicciones hacemos una nueva suposición y cuando no haya contradicciones llegamos a la solución. caso 1 caso 2 caso 3 caso 4 Andrés : V-I F-I F-I F Eduardo: F-C V-I F-I F-I Jesús: F-I-C F-C-C V-I-I F-I-C Rafael: F-C F-C F-C V-I En la tabla hemos utilizado las siguientes notaciones: F- falso V – Verdadero I- inocente C – culpable. Caso 1: Si suponemos que Andrés dice verdad, es inocente, entonces Eduardo y Rafael son culpables y Jesús sería inocente y culpable a la vez, lo que es imposible y se descarta esta posibilidad. Caso 2: Si suponemos que Eduardo dice la verdad este sería inocente al igual que Andrés, entonces Jesús y Rafael serían culpables y como es uno solo el culpable se descarta esta posibilidad. Caso 3: Suponiendo que Jesús diga la verdad, deducimos fácilmente que Andrés, Eduardo y Jesús son inocentes y solo Rafael aparece como único culpable y esta es una posible solución. Caso 4: Si Rafael dice verdad llegamos rápidamente a una contradicción, pues Jesús sería inocente y culpable a la vez y esto es imposible. Haciendo una valoración de los cuatro casos podemos concluir que el único en que no se llega a una contradicción es en el tercero, por lo tanto Rafael es el culpable. 2) En cierto planeta cada habitante es veraz o mentiroso. Al llegar a este planeta encontramos tres extraterrestres. ET1 dice: "ET2 y yo somos iguales" ET2 dice: "ET3 es veraz" ET3 dice: "ET1 y yo somos diferentes" ¿Cómo es cada uno de ellos veraz o mentiroso? R/ Este puede ser llevado a una tabla, diferenciando dos casos, como aparece a continuación: Caso 1: Si ET1 dice verdad, entonces ET2 es veraz al igual que ET3, llegando a una contradicción ya que ET3 plantea que él y ET1 son diferentes y son iguales, por lo tanto desechamos esta posibilidad. Caso 2: Supongamos que ET2 dice verdad, entonces ET3 es veraz y ET1 es mentiroso y como no hay contradicción esta es la solución. ET1 ET2 ET3 caso 1 V V V caso 2 F V V 3) Eduardo miente los miércoles, jueves y viernes y dice la verdad el resto de la semana, Andrés miente los domingos, lunes y martes y dice la verdad el resto de la semana. Si ambos dicen "mañana es un día en el que yo miento" ¿Qué día de la semana será mañana? R/ Hagamos una tabla donde aparezcan Eduardo, Andrés y los días de la semana, marquemos los días que dicen verdad con V y los que mienten por F. Haciendo un análisis parecido a los anteriores llegamos a la conclusión de que ese día se obtiene cuando el valor de verdad de ambos se cambia al día siguiente y esto solo ocurre cuando se pasa de martes para miércoles, luego concluimos que mañana será miércoles. L Eduardo V Andrés F M V F M F V J F V V F V S V V D V F _______________________________________________________________________________ R/ Este puede ser llevado a una tabla, diferenciando dos casos, como aparece a continuación: Caso 1: Si ET1 dice verdad, entonces ET2 es veraz al igual que ET3, llegando a una contradicción ya que ET3 plantea que él y ET1 son diferentes y son iguales, por lo tanto desechamos esta posibilidad. Caso 2: Supongamos que ET2 dice verdad, entonces ET3 es veraz y ET1 es mentiroso y como no hay contradicción esta es la solución. Elaborado por Cynthia Rodas