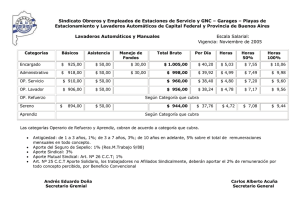
Aprendizaje por refuerzo Aprendizaje por refuerzo
Anuncio

Aprendizaje por refuerzo
José M. Sempere
Departamento de Sistemas Informáticos y Computación
Universidad Politécnica de Valencia
Aprendizaje por refuerzo
1.
2.
3.
4.
5.
Introducción al aprendizaje por refuerzo
Modelos de Decisión de Markov. Taxonomía de los métodos de aprendizaje
Métodos basados en técnicas de Programación Dinámica
Métodos libres de modelo
Métodos basados en el modelo
Bibliografía
•
T. Mitchell.
Mitchell. Machine Learning.
Learning. McGrawMcGraw-Hill. 1997.
•
R. Sutton,
Sutton, A. Barto.
Barto. Reinforcement Learning.
Learning. An Introduction.
Introduction. The MIT Press.
Press. 1998.
•
B. Sierra. Aprendizaje automático: conceptos básicos y avanzados.
avanzados.
PearsonPearson-Prentice Hall. 2006.
1
Aprendizaje por refuerzo
Algunas características:
(1) Es completo (contempla el problema en su totalidad, mediante funciones objetivo)
(2) Es interactivo (recibe información del entorno y puede modificar el mismo)
(3) Es no supervisado (sustituye la información supervisada por información del tipo
acción/reacción)
(4) Es dirigido por objetivos (el fin del aprendizaje es alcanzar un máximo)
(5) El aprendiz debe explotar las acciones que le beneficien y explorar nuevas acciones
Elementos del aprendizaje por refuerzo:
(1) La política que define el comportamiento del aprendiz en cada momento
(2) La función de recompensa que define el objetivo a alcanzar
(3) La funciòn de evaluación que permite establecer la respuesta recibida a partir de
cada posible acción
(4) Opcionalmente un modelo del entorno
Un ejemplo: El trestres-enen-raya (tic-tac-toe)
X
X
X
X
• Los estados del entorno son las posibles configuraciones de O y X ( o blancos) en las
casillas del tablero
• A cada configuración se le asigna la probabilidad de ganar el juego desde ese estado
• Las configuraciones con tres-en-raya tienen probabilidad 0 (o 1)
• El resto de configuraciones tienen inicialmente probabilidad 0.5
• Las probabilidades se actualizan mediante un criterio de aprendizaje por diferencias
temporales siguiendo una ecuación del estilo
V(s) = V(s) + α [V(s’) – V(s)]
donde s’ es el estado alcanzado a partir de s y α es un parámetro que influencia el ratio
de aprendizaje
2
Esquema general del aprendizaje por refuerzo
aprendiz
recompensa
estado
S = { s0, s1, … } es el conjunto de estados del
entorno
A = { a0, a1, … } es el conjunto de acciones que
puede realizar el aprendiz
ri es la recompensa que recibe el aprendiz tras
haber realizado la acción ai en el estado si
acción
entorno
s0
a0
r0
s1
a1
r1
s2
Objetivo: Aprender una política π: S → A que maximice una función de recompensa
acumulada con descuento por ejemplo
∞
V π ( st ) = rt + γ ⋅ rt +1 + γ 2 ⋅ rt + 2 + ... = ∑ γ i ⋅ rt +i
γ es denominado ratio de descuento
i =0
y pondera las recompensas futuras respecto de las
actuales (toma valores entre 0 y 1).
π
A la política óptima la denotaremos por π* y se puede expresar como π * = argmax V ( s ), (∀s )
π
Denominaremos episodio a una secuencia de acciones-estados completa, es decir desde
el inicio hasta un estado objetivo o sumidero. El aprendizaje se divide en episodios de forma
natural (p.ej. partidas de un juego, secuencias de movimientos hasta llegar a una meta, etc.)
Procesos de decisión de Markov
Un Proceso de Decisión de Markov (MDP) se define mediante la tupla <S,A,T,R> donde
S es un conjunto de estados
A es un conjunto de acciones
T : S × A → Pr(S) es una distribución de probabilidad
R : S × A → R es una función de refuerzo
Un MDP es finito si S y A son conjuntos finitos
La propiedad de Markov
Pr{st+1=s’, rt+1=r | st , at, rt, st-1, at-1, …, r1, s0, a0} = Pr{st+1=s’, rt+1=r | st, at}
En este caso se cumple que
T(s,a,s’) = Pr{st+1=s’ | st=s, at=a}
R(s,a) = E{rt+1 | st=s, at=a}
3
Funciones de valor
Las funciones de valor evalúan las políticas que ejerce el aprendiz, es decir la secuencia
de acciones y estados que el aprendiz ejecuta y en los que se sitúa a lo largo del tiempo.
La función de valor-estado (state-value)
∞
V π ( s ) = Eπ {∑ γ i ⋅ rt +i +1 | st = s}
i =0
La función de valor-acción (action-value)
∞
Qπ ( s, a ) = Eπ {Rt | st = s, at = a} = Eπ {∑ γ i ⋅ rt +i +1 | st = s, at = a}
i =0
Para una política óptima π* se maximizan las funciones anteriores
V * ( s ) = max V π ( s ) (∀s ∈ S )
π
Q * ( s, a) = max Qπ ( s, a) (∀s ∈ S ) (∀a ∈ A)
π
Una taxonomía de los métodos de aprendizaje por refuerzo
Los métodos de resolución en un problema de aprendizaje por refuerzo (considerando
que sea un Proceso de Decisión de Markov) se pueden clasificar en función del
conocimiento que se tenga del modelo
Resolución a partir de un conocimiento completo
Se conocen el conjunto de estados y acciones, la función de transición
de estados y la función de refuerzo.
La resolución se basa en la Programación Dinámica (PD) como técnica de
optimización.
Resolución a partir de un conocimiento incompleto
No se conoce el modelo. Posibles soluciones
(a) Aplicar técnicas sin el conocimiento del modelo (métodos libres de modelo)
(b) Aprender el modelo y la política del mismo (métodos basados en el modelo)
4
Métodos basados en técnicas de Programación Dinámica (I)
Los métodos parten de un conocimiento completo del modelo. Se cumplen
las ecuaciones de optimalidad de Bellman
Principio de optimalidad de Bellman
Una política óptima tiene la propiedad de que cualesquiera que sean el estado inicial y la primera decisión
tomada, el resto de decisiones deben constituir una política óptima respecto al estado resultante de la
primera decisión. Se cumplen las siguientes ecuaciones
V * ( s) = max E{rt +1 + γV * ( st +1 ) | st = s, at = a} = max ∑ T ( s, a, s' )[ R ( s, a) + γV * ( s' )]
a
a
a
Q* ( s, a ) = E{rt +1 + max Q * ( st +1 , a ' ) | st = s, at = a} = ∑ T ( s, a, s ' )[ R( s, a ) + γ max Q * ( s ' , a ' )]
a
s'
a'
Dado que las anteriores ecuaciones son recursivas, utilizamos esquemas de Programación Dinámica
para resolverlas.
Métodos basados en técnicas de Programación Dinámica (II)
Inicialización: (∀ s ∈ S) V(s) ∈ R y π(s) ∈ A arbitrarios
Método:
Repetir
(1) Evaluación de la Política
Repetir
∆←0
V(s) ← Σs’ T(s,π(s),s’)[R(s,π(s)) + γV(s’)]
∆ ← max(∆,|v-V(s)|)
hasta que ∆ < θ (entero positivo)
(2) Mejora de la Política
política_estable ← cierto
Para cada s ∈ S
b ← π(s)
π(s) ← argmaxa Σs’ T(s,a,s’)[R(s,a) + γV(s’)]
Si b ≠ π(s)
entonces política_estable ← falso
hasta que política_estable = cierto
Algoritmo de Iteración de Política
5
Métodos basados en técnicas de Programación Dinámica (III)
Inicialización: (∀ s ∈ S) V(s)=0 (o cualquier valor arbitrario)
Método:
Repetir
∆←0
Para cada s ∈ S
v ← V(s)
V(s) ← maxaΣs’ T(s,a,s’)[R(s,a) + γV(s’)]
∆ ← max(∆,|v-V(s)|)
hasta que ∆ < θ (entero positivo)
Dar como salida una política determinista π tal que
π(s) = argmaxa Σs’ T(s,a,s’)[R(s,a) + γV(s’)]
Algoritmo de Iteración de Valor
Métodos libres de modelo
Los métodos parten de un conocimiento completo del conjunto de estados y del
conjunto de acciones modelo. No se conocen los efectos de las acciones sobre
el entorno (interacción).
Posibles estrategias:
(1) Extraer secuencias completas de comportamiento del aprendiz y
basar el aprendizaje de la política en esas secuencias (métodos
Monte Carlo)
(2) Basar el aprendizaje en las acciones inmediatas que realice el
aprendiz (métodos de Diferencias temporales ó TD, Aprendizaje-Q)
(3) Establecer secuencias intermedias para el aprendizaje (métodos
TD(λ))
Variantes dentro de las estrategias:
(1) Métodos basados en la política: La política que se está aprendiendo
se aplica sobre el entorno.
(2) Métodos fuera de política: La política de interacción sobre el entorno
es independiente de la que se está aprendiendo
6
Métodos Monte Carlo
Inicialización: (∀ s ∈ S) (∀ a ∈ A)
Q(s,a) ← valor arbitrario
π(s) ← valor arbitrario
ganancias(s,a) ← lista vacía
Método:
Repetir
Iniciar un episodio usando inicio exploratorio y π
Para cada par (s,a) que aparece en el episodio
R ← ganancia obtenida tras la primera ocurrencia del par (s,a)
Añadir R a ganancias(s,a)
Q(s,a) ← promedio(ganancias(s,a))
Para cada s en el episodio
π(s) ← argmaxa Q(s,a)
siempre
Algoritmo Monte Carlo ES
(Monte Carlo con inicio exploratorio)
Métodos mediante Diferencias Temporales (I)
Inicialización: V(s) arbitrariamente
Método:
Repetir (para cada episodio)
a ← acción dada por π y s
Ejecutar la acción a. Observar el refuerzo recibido r y el estado siguiente s’
V(s) ← V(s) + α[r + γV(s’)-V(s)]
s ← s’
hasta que s’ sea un estado terminal
(α es un parámetro que pondera las actualizaciones con respecto a los valores anteriores.
Para dominios deterministas α=1)
Algoritmo TD(0)
(aprendizaje de la función valor-estado)
7
Métodos mediante Diferencias Temporales (II)
Inicialización: Q(s,a) arbitrariamente
Método:
Repetir (para cada episodio)
Inicializar s
Repetir para cada paso del episodio
Seleccionar una acción a a partir de s utilizando la política derivada de Q
Ejecutar la acción a. Observar el refuerzo recibido r y el estado siguiente s’
Actualizar la tabla Q(s,a)
Q(s,a) ← Q(s,a) + α[r + γ maxa’Q(s’,a’) - Q(s,a)]
s ← s’
hasta que s’ sea un estado terminal
(α es un parámetro que pondera las actualizaciones con respecto a los valores anteriores.
Para dominios deterministas α=1)
Algoritmo de Aprendizaje-Q
(aprendizaje de la función valor-acción,
método fuera de la política)
Métodos mediante Diferencias Temporales (III)
Inicialización: Q(s,a) arbitrariamente
Método:
Repetir (para cada episodio)
Inicializar s
Seleccionar una acción a a partir de s utilizando la política derivada de Q
Repetir para cada paso del episodio
Ejecutar la acción a. Observar el refuerzo recibido r y el estado siguiente s’
Elegir a’ a partir de s’ utilizando la política derivada de Q
Actualizar la tabla Q(s,a)
Q(s,a) ← Q(s,a) + α[r + γ maxa’Q(s’,a’) - Q(s,a)]
s ← s’
a ← a’
hasta que s’ sea un estado terminal
(α es un parámetro que pondera las actualizaciones con respecto a los valores anteriores.
Para dominios deterministas α=1)
Algoritmo SARSA
(aprendizaje de la función valor-acción,
método basado en la política)
8
Métodos basados en el modelo
Los métodos fuerzan el aprendizaje del modelo (aprendizaje de las funciones T y
R) y aplican técnicas de Programación Dinámica sobre el mismo.
Inicialización: Q(s,a) y Modelo(s,a) arbitrariamente
Método:
Repetir (siempre)
Inicializar s
Seleccionar una acción a a partir de s utilizando la política derivada de Q
Q(s,a) ← Q(s,a) + α[r + γ maxa’Q(s’,a’) - Q(s,a)]
Modelo(s,a) ← (s’,r)
s ← s’
Repetir N veces
s ← estado ya visitado elegido aleatoriamente
a ← acción aleatoria ejecutada anteriormente desde s
(s’,r) ← Modelo(s,a)
Q(s,a) ← Q(s,a) + α[r + γ maxa’Q(s’,a’) - Q(s,a)]
(α es un parámetro que pondera las actualizaciones con respecto a los valores anteriores.
N es un parámetro de actualizaciones de la función que fija el usuario)
Algoritmo Dyna-Q
(entorno determinista)
9