POTENCIA Model (1)

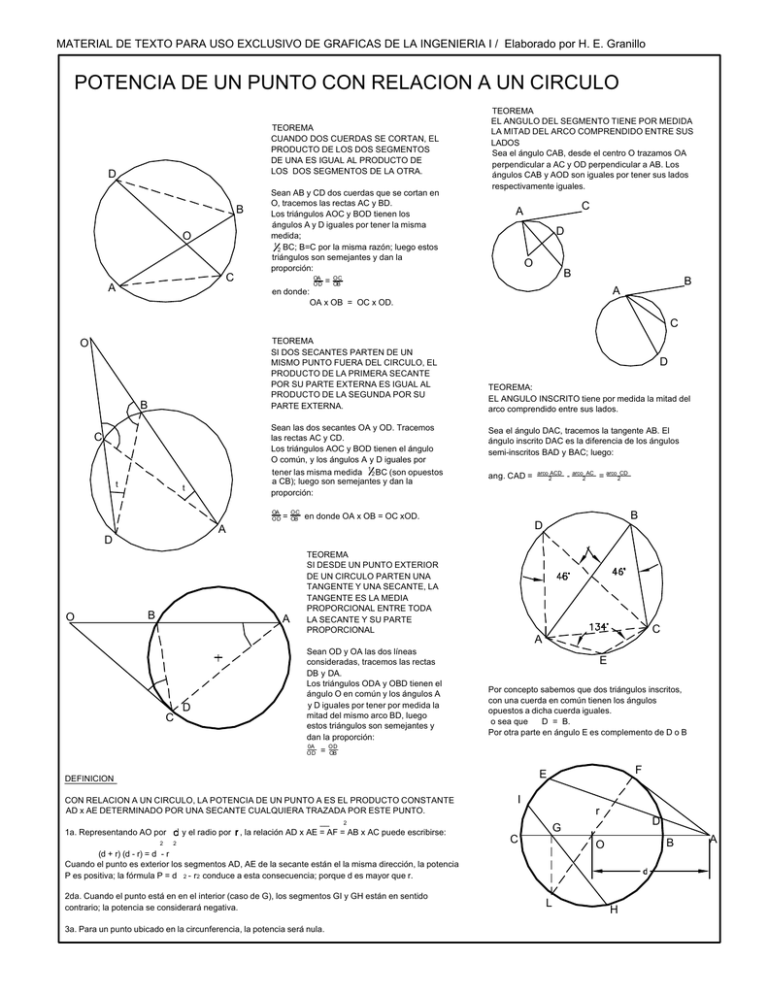
MATERIAL DE TEXTO PARA USO EXCLUSIVO DE GRAFICAS DE LA INGENIERIA I / Elaborado por H. E. Granillo
POTENCIA DE UN PUNTO CON RELACION A UN CIRCULO
TEOREMA
CUANDO DOS CUERDAS SE CORTAN, EL
PRODUCTO DE LOS DOS SEGMENTOS
DE UNA ES IGUAL AL PRODUCTO DE
LOS DOS SEGMENTOS DE LA OTRA.
D
B
O
Sean AB y CD dos cuerdas que se cortan en
O, tracemos las rectas AC y BD.
Los triángulos AOC y BOD tienen los
ángulos A y D iguales por tener la misma
medida;
1 BC; B=C por la misma razón; luego estos
2
triángulos son semejantes y dan la
proporción:
C
A
OA
OD
=
TEOREMA
EL ANGULO DEL SEGMENTO TIENE POR MEDIDA
LA MITAD DEL ARCO COMPRENDIDO ENTRE SUS
LADOS
Sea el ángulo CAB, desde el centro O trazamos OA
perpendicular a AC y OD perpendicular a AB. Los
ángulos CAB y AOD son iguales por tener sus lados
respectivamente iguales.
C
A
D
O
B
OC
OB
B
A
en donde:
OA x OB = OC x OD.
C
TEOREMA
SI DOS SECANTES PARTEN DE UN
MISMO PUNTO FUERA DEL CIRCULO, EL
PRODUCTO DE LA PRIMERA SECANTE
POR SU PARTE EXTERNA ES IGUAL AL
PRODUCTO DE LA SEGUNDA POR SU
PARTE EXTERNA.
O
B
Sean las dos secantes OA y OD. Tracemos
las rectas AC y CD.
Los triángulos AOC y BOD tienen el ángulo
O común, y los ángulos A y D iguales por
tener las misma medida 1 2 BC (son opuestos
a CB); luego son semejantes y dan la
proporción:
C
t
t
OA
OD
OC
OB
TEOREMA:
EL ANGULO INSCRITO tiene por medida la mitad del
arco comprendido entre sus lados.
Sea el ángulo DAC, tracemos la tangente AB. El
ángulo inscrito DAC es la diferencia de los ángulos
semi-inscritos BAD y BAC; luego:
ang. CAD =
B
A
arco ACD
2
- arco_AC
= arco_CD
2
2
B
en donde OA x OB = OC xOD.
D
A
D
O
=
D
TEOREMA
SI DESDE UN PUNTO EXTERIOR
DE UN CIRCULO PARTEN UNA
TANGENTE Y UNA SECANTE, LA
TANGENTE ES LA MEDIA
PROPORCIONAL ENTRE TODA
LA SECANTE Y SU PARTE
PROPORCIONAL
C
A
C
D
Sean OD y OA las dos líneas
consideradas, tracemos las rectas
DB y DA.
Los triángulos ODA y OBD tienen el
ángulo O en común y los ángulos A
y D iguales por tener por medida la
mitad del mismo arco BD, luego
estos triángulos son semejantes y
dan la proporción:
0A
OD
=
E
Por concepto sabemos que dos triángulos inscritos,
con una cuerda en común tienen los ángulos
opuestos a dicha cuerda iguales.
o sea que
D = B.
Por otra parte en ángulo E es complemento de D o B
OD
OB
F
E
DEFINICION
CON RELACION A UN CIRCULO, LA POTENCIA DE UN PUNTO A ES EL PRODUCTO CONSTANTE
AD x AE DETERMINADO POR UNA SECANTE CUALQUIERA TRAZADA POR ESTE PUNTO.
__
2
1a. Representando AO por
y el radio por , la relación AD x AE = AF = AB x AC puede escribirse:
2
2
I
r
D
G
C
B
O
(d + r) (d - r) = d - r
Cuando el punto es exterior los segmentos AD, AE de la secante están el la misma dirección, la potencia
P es positiva; la fórmula P = d 2 - r2 conduce a esta consecuencia; porque d es mayor que r.
2da. Cuando el punto está en en el interior (caso de G), los segmentos GI y GH están en sentido
contrario; la potencia se considerará negativa.
3a. Para un punto ubicado en la circunferencia, la potencia será nula.
L
H
A
MATERIAL DE TEXTO PARA USO EXCLUSIVO DE GRAFICAS DE LA INGENIERIA I / Elaborado por H. E. Granillo
EL EJE RADICAL ES EL LUGAR GEOMÉTRICO DE LOS PUNTOS DESDE LOS QUE
SE PUEDEN TRAZAR TANGENTES IGUALES A DOS CIRCULOS.
EJE RADICAL
G
TEOREMA:
El lugar de los puntos de
igual potencia con relación a
dos círcunferencias es una
perpendicular a la recta de
los centros.
Este lugar se llama EJE
RADICAL de las dos
circunferencias.
---------------------------Sean las circunferencias A y
B de radios a y b
respectivamente, y C un
punto igual de potencia con
relación a estas
circunferencias.
Desde el punto C bajemos la
perpendicular CD sobre la
recta de los centros; se
necesita comprobar que CD
es el eje radical.
C
H
F
D
A
B
E
N
M
C
En efecto, haciendo AC = d y BC = d
potencia, se tiene:
2
2
2
2
2
1=
2
1,
puesto que C es un punto de igual
a
2
b
d - a = d 1- b
ó
d-d
a-b
2
m
El punto C es tal que la diferencia de los cuadrados de sus distancias a los
puntos fijos A y B sea constante; y siempre será una perpendicular a AB, para
nuestro caso la recta CD; y se explica:
A
2
EJE RADICAL
A
PT2
C
O2
D
PT8
EJE RADICAL
PT6
B
Se presentan las distintas rectas
tangentes posibles a dos arcos de
radios diferentes, O1 y O2.
Existen 4 posibles tangentes entre
ambos arcos:
PT1-PT2; PT3-PT4; PT5-PT6; y
PT7-PT8
(PT = Punto de Tangencia)
Los puntos medios de las tangentes se
indican por los puntos A, B, C y D.
PT4
PT7
2
ILUSTRACION DEL EJE RADICAL DE
DOS ARCOS DE DIFERENTE
TAMAÑO.
PT5
m
B
o' 2 cm = k 2
k2
sea
m=
2c
Luego, la distancia m es constante, y C pertenece a
una perpendicular levantada en D sobre AB.
La recta CM es la mediana del triángulo ACB
PT3
O1
D
a - b = 2 cm
Sea C un punto del lugar de los puntos tales que la diferencia de los cuadrados
de las distancias de los puntos A y B sea una constante "k".
En el triángulo ABC tenemos:
PT1
M
El punto "m" es el punto medio entre
ambos centros. Nótese que el eje
radical se encuentra más cercano al
centro de la circunferencia de radio
menor.
MATERIAL DE TEXTO PARA USO EXCLUSIVO DE GRAFICAS DE LA INGENIERIA I / Elaborado por H. E. Granillo
Conceptualmente la tangencia es aquella relación geométrica entre un arco y una recta, o entre dos arcos que da por
resultado un punto en común.
TANGENCIA:
Se llama TANGENTE a una recta cualquiera que no tiene más que un punto en común a una circunferencia. Cuando
una recta es tangente a una circunferencia, la circunferencia es igualmente tangente a la recta.
La tangente debe considerarse
como el límite de las posiciones
que toma una secante CD que
gira al rededor del punto C,
tendiendo al segundo punto de
intersección a confundirse con
el primero.
D
D
RECTA NORMAL en un punto
de una curva es la
perpendicular a la tangente
trazada por este mismo punto.
D
A
B
C
A
B
C
Sea OC el radio trazado en el
punto de contaco de la tangente
AB.
Estando fuera del círculo todos
los puntos de AB con excepción
de C, por tanto OC es la línea
más corta que se puede trazar
desde el punto O a la recta AB.
Por tanto OC es perpendicular a
AB, y recíprocamente AB es
perpendicular a OC.
O
A
B
C
D
TEOREMA: "Toda recta
perpendicular a la extremidad
de un radio es tangente a la
circunferencia."
El radio OC es al mismo tiempo
perpendicular a AB, y
cualquiera otra recta OD es
oblícua, por consiguiente mayor
que el radio OC (OD > OC), y el
punto D queda fuera del círculo.
Así es que la recta AB no tiene
más que el punto C común con
la circunferencia.
O
RECIPROCA: La recta
tangente a una circunferencia
es perpendicular al radio que
termina en el punto de
tangencia (PT).
D
COROLARIOS:
1.- En todo punto de la circunferencia se le pueden trazar una tangente, y solo
una;
2.- La perpendicular trazada del centro sobre la tangente pasa por el punto de
tangencia (PT);
3.- Todos los puntos de la tangente son exteriores al círculo, con excepción del
punto de tangencia;
4.- Se puede trazr a una circunferencia dos tangentes paralelas a una
dirección dada; son perpendiculares en los extremos del diámetro
perpendicular a ésta dirección.
DEFINICION: Dos circunferencias son
tangentes entre sí cuando se tocan en un
solo punto. Si dos circunferencias se
cortan, se les denomina circunferencias
secantes.
TEOREMA: Si dos circunferencias son
tangentes, el punto de tangencia está
sobre la recta que une los centros (son
colineales). Si no fuera así este punto
debería tener otro punto común simétrico
del primero y entonces estas
circunferencias serían secantes.
O
O'
PT
m
TEOREMA: Si dos circunferencias son
tangentes, la perpendicular levantada
sore la recta de los centros por el punto
de tangencia, es una tangente común a
ambas circunferencias; porque esta recta
es perpendicular a la extremidad de cada
uno de los radios. (Principio de
Tangencia).
O'
B
A
0
n
CIRCUNFERENCIAS SECANTES
O'
PT
O
O'
CIRCUNFERENCIAS TANGENTES
A
B
O