Análisis de la varianza. - Universidad de Castilla

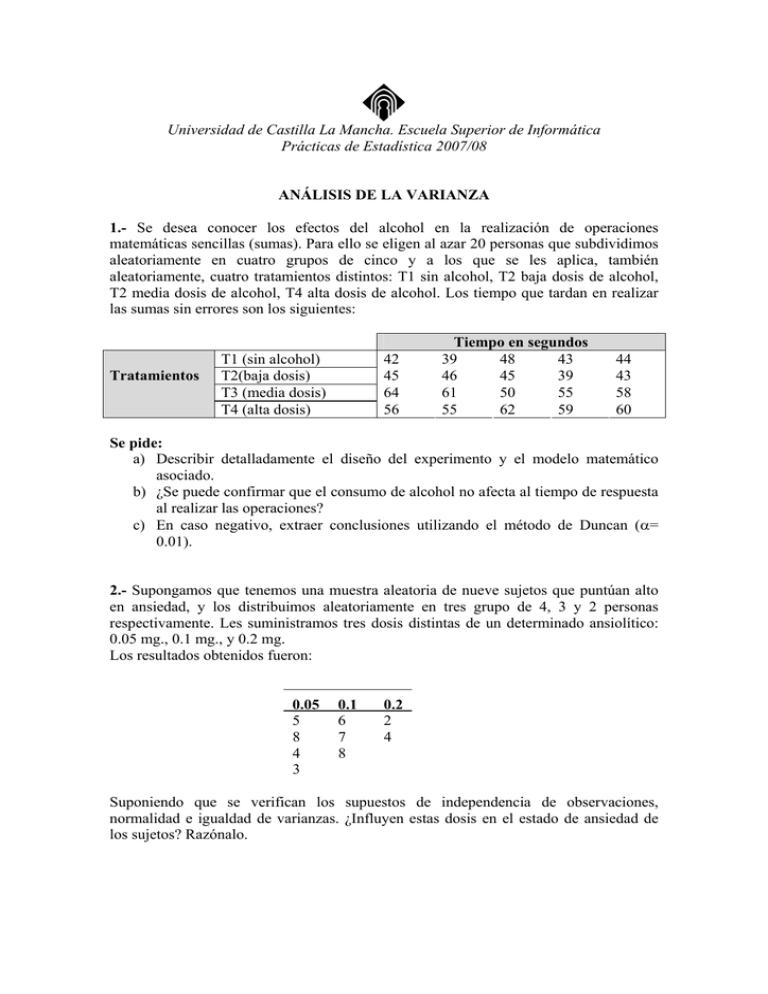
Universidad de Castilla La Mancha. Escuela Superior de Informática
Prácticas de Estadística 2007/08
ANÁLISIS DE LA VARIANZA
1.- Se desea conocer los efectos del alcohol en la realización de operaciones
matemáticas sencillas (sumas). Para ello se eligen al azar 20 personas que subdividimos
aleatoriamente en cuatro grupos de cinco y a los que se les aplica, también
aleatoriamente, cuatro tratamientos distintos: T1 sin alcohol, T2 baja dosis de alcohol,
T2 media dosis de alcohol, T4 alta dosis de alcohol. Los tiempo que tardan en realizar
las sumas sin errores son los siguientes:
Tratamientos
T1 (sin alcohol)
T2(baja dosis)
T3 (media dosis)
T4 (alta dosis)
42
45
64
56
Tiempo en segundos
39
48
43
46
45
39
61
50
55
55
62
59
44
43
58
60
Se pide:
a) Describir detalladamente el diseño del experimento y el modelo matemático
asociado.
b) ¿Se puede confirmar que el consumo de alcohol no afecta al tiempo de respuesta
al realizar las operaciones?
c) En caso negativo, extraer conclusiones utilizando el método de Duncan (α=
0.01).
2.- Supongamos que tenemos una muestra aleatoria de nueve sujetos que puntúan alto
en ansiedad, y los distribuimos aleatoriamente en tres grupo de 4, 3 y 2 personas
respectivamente. Les suministramos tres dosis distintas de un determinado ansiolítico:
0.05 mg., 0.1 mg., y 0.2 mg.
Los resultados obtenidos fueron:
0.05
5
8
4
3
0.1
6
7
8
0.2
2
4
Suponiendo que se verifican los supuestos de independencia de observaciones,
normalidad e igualdad de varianzas. ¿Influyen estas dosis en el estado de ansiedad de
los sujetos? Razónalo.
3.- Se sospecha que la temperatura del medio en el que se activan las baterías afecta a su
vida activa. Se prueban 30 baterías homogéneas, 6 a cada una de 5 temperaturas y se
obtienen los datos que muestra la siguiente tabla que indica la vida activada en
segundos:
0
55
55
57
54
54
56
TEMPERATURA (º C)
25
50
75
60
70
72
61
72
72
60
73
72
60
68
70
60
77
68
60
77
69
100
65
66
60
64
65
65
a) Realizar un análisis de varianza y establecer una conclusión sobre si la sospecha
es cierta o no.
b) De serlo, indicar entre qué temperaturas hay diferencias en las medias de vida
activa de las baterías.
c) Calcular intervalos de confianza para esas diferencias.
4.- Supongamos que disponemos de un conjunto de pinos clasificados por alturas (en
metros) y por especies según los datos de la siguiente tabla:
Especie
Pinea
Pinaster
Silvestris
Pinea
Pinaster
Laricio
Halapensis
Laricio
Silvestris
Silvestris
Pinaster
Pinea
Pinea
Halapensis
Pinaster
Altura
8.52
6.45
7.41
7.15
8.73
7.55
6.54
7.74
8.65
8.81
8.52
6.43
6.21
7.07
8.83
Especie
Pinaster
Laricio
Silvestris
Laricio
Pinaster
Pinea
Halapensis
Pinaster
Silvestris
Pinea
Pinaster
Silvestris
Laricio
Pinaster
Pinaster
Altura
8.53
7.84
8.59
7.41
8.94
8.13
7.17
8.40
8.87
6.12
8.91
8.81
7.40
8.19
8.56
a) Ajustar los datos a un modelo del análisis de la varianza para contrastar si
pueden considerarse iguales todas las especies de pinos en cuanto a altura.
b) Agrupar los datos en grupos homogéneos de especies en cuanto a algura
realizando comparaciones de especies dos a dos.
c) Hallar intervalos de confianza para las diferencias de alturas medias entre los
diferentes pares de especies.