ejemplo de estimación paramétrica usando R
Anuncio
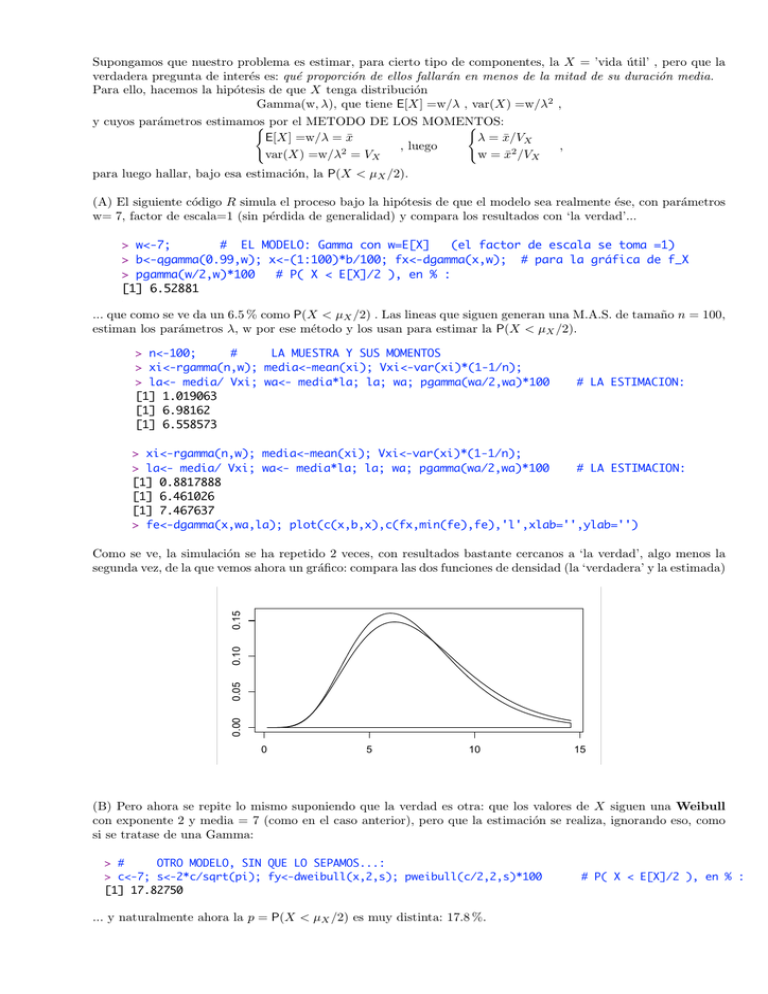
Supongamos que nuestro problema es estimar, para cierto tipo de componentes, la X = ’vida útil’ , pero que la verdadera pregunta de interés es: qué proporción de ellos fallarán en menos de la mitad de su duración media. Para ello, hacemos la hipótesis de que X tenga distribución Gamma(w, λ), que tiene E[X] =w/λ , var(X) =w/λ2 , y cuyos parámetros estimamos ! por el METODO DE LOS MOMENTOS: ! E[X] =w/λ = x̄ λ = x̄/VX , luego , 2 var(X) =w/λ = VX w = x̄2 /VX para luego hallar, bajo esa estimación, la P(X < µX /2). (A) El siguiente código R simula el proceso bajo la hipótesis de que el modelo sea realmente ése, con parámetros w= 7, factor de escala=1 (sin pérdida de generalidad) y compara los resultados con ‘la verdad’... 0.00 0.05 0.10 0.15 > w<-7; # EL MODELO: Gamma con w=E[X] (el factor de escala se toma =1) > b<-qgamma(0.99,w); x<-(1:100)*b/100; fx<-dgamma(x,w); # para la gráfica de f_X > w<-7; # EL MODELO: Gamma con w=E[X] (el factor de escala se toma =1) > pgamma(w/2,w)*100 # P( X < E[X]/2 ), en % : >> b<-qgamma(0.99,w); x<-(1:100)*b/100; fx<-dgamma(x,w); para la gráfica f_X w<-7; # EL MODELO: Gamma con w=E[X] (el factor#de escala se tomade =1) [1] 6.52881 >> pgamma(w/2,w)*100 # P( X < E[X]/2 ),fx<-dgamma(x,w); en % : b<-qgamma(0.99,w); x<-(1:100)*b/100; # para la gráfica de f_X > [1] 6.52881 > pgamma(w/2,w)*100 # P(X P( X<<µ E[X]/2 ),lineas en %que : siguen generan una M.A.S. de tamaño n = 100, ... que> como se ve da un# 6.5 % como /2) . MOMENTOS Las n<-100; LA MUESTRA YX SUS > [1] 6.52881 estiman los parámetros λ, w media<-mean(xi); por ese método y los Vxi<-var(xi)*(1-1/n); usan para estimar la P(X < µX /2). > xi<-rgamma(n,w); >> n<-100; # LA MUESTRA Y SUS MOMENTOS > la<- media/ Vxi; wa<- media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: n<-100; # LA MUESTRA Y SUSVxi<-var(xi)*(1-1/n); MOMENTOS >> xi<-rgamma(n,w); media<-mean(xi); [1] 1.019063 xi<-rgamma(n,w); media<-mean(xi); >> la<media/ Vxi; wa<media*la; la;Vxi<-var(xi)*(1-1/n); wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: [1] 6.98162 > la<media/ Vxi; wa<- media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: [1] 1.019063 [1] 6.558573 [1] 1.019063 [1] 6.98162 > [1] fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') [1] 6.98162 6.558573 > >[1] n<-100; # LA MUESTRA Y SUS MOMENTOS 6.558573 fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') > >> xi<-rgamma(n,w); media<-mean(xi); fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') n<-100; # LA MUESTRA Y SUSVxi<-var(xi)*(1-1/n); MOMENTOS > >> la<media/ Vxi; la;Vxi<-var(xi)*(1-1/n); wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: n<-100; # wa<LA media*la; MUESTRA Y SUS MOMENTOS xi<-rgamma(n,w); media<-mean(xi); [1] 0.8817888 xi<-rgamma(n,w); media<-mean(xi); >> la<media/ Vxi; wa<media*la; la;Vxi<-var(xi)*(1-1/n); wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: [1] 6.461026 > la<media/ Vxi; wa<- media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION: [1] 0.8817888 [1] 7.467637 [1] 0.8817888 [1] 6.461026 > [1] fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') [1] 6.461026 7.467637 > >[1] 7.467637 fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') > >> # fe<-dgamma(x,wa,la); OTRO MODELO, SIN plot(c(x,b,x),c(fx,min(fe),fe),'l',xlab='',ylab='') QUE LO SEPAMOS...: > > c<-7; fy<-dweibull(x,2,c); P( X <a E[X]/2 ), en : > ve, # la simulación OTRO MODELO, QUE pweibull(c/2,2,c)*100 SEPAMOS...: Como se se ha SIN repetido 2LOveces, con resultados bastante #cercanos ‘la verdad’, algo% menos la > # OTRO MODELO, SIN QUE LO SEPAMOS...: [1] 22.11992 c<-7; pweibull(c/2,2,c)*100 # P( X <(laE[X]/2 ), en : segunda> vez, de lafy<-dweibull(x,2,c); que vemos ahora un gráfico: compara las dos funciones de densidad ‘verdadera’ y la%estimada) > c<-7; fy<-dweibull(x,2,c); pweibull(c/2,2,c)*100 # P( X < E[X]/2 ), en % : > [1] xi<-rweibull(n,2,c); media<-mean(xi); Vxi<-var(xi)*(1-1/n); 22.11992 [1] 22.11992 > >la<-media / Vxi; wa<-media*la; la; wa; Vxi<-var(xi)*(1-1/n); pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: xi<-rweibull(n,2,c); media<-mean(xi); xi<-rweibull(n,2,c); media<-mean(xi); >> la<-media la; wa; Vxi<-var(xi)*(1-1/n); pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: [1] 0.6122461 / Vxi; wa<-media*la; > la<-media [1] 0.6122461/ Vxi; wa<-media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: [1] 3.739277 [1] 0.6122461 [1] 3.739277 [1] 15.38061 [1] 3.739277 15.38061 > [1] fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') [1] 15.38061 > fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') > fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') 0 > w<-7; # 5 EL MODELO: Gamma con w=E[X] 10 15 (el factor de escala se toma =1) (B) ahora se repite lox<-(1:100)*b/100; mismo suponiendo fx<-dgamma(x,w); que la verdad es otra: de X > Pero b<-qgamma(0.99,w); # que paralos lavalores gráfica de siguen f_X una Weibull con > exponente n<-100; 2 y media = 7 (como en el caso anterior), pero que la estimación se realiza, ignorando eso, como si >se tratase de una Gamma: > > # OTRO MODELO, SIN QUE LO SEPAMOS...: > c<-7; s<-2*c/sqrt(pi); fy<-dweibull(x,2,s); pweibull(c/2,2,s)*100 # P( X < E[X]/2 ), en % : [1] 17.82750 > ... >y xi<-rweibull(n,2,s); naturalmente ahora la p media<-mean(xi); = P(X < µX /2) es Vxi<-var(xi)*(1-1/n); muy distinta: 17.8 %. > la<-media / Vxi; wa<-media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: [1] 0.6276832 [1] 4.525886 [1] 12.35883 > fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') 0.00 0.05 0.10 0.15 > b<-qgamma(0.99,w); x<-(1:100)*b/100; fx<-dgamma(x,w); # para la gráfica de f_X > n<-100; > > > # QUE LOdeSEPAMOS...: El código queOTRO sigueMODELO, repite laSIN operación antes, produce el resultado (en el que naturalmente los ‘parámetros > c<-7;nos<-2*c/sqrt(pi); # peor P( X que < E[X]/2 estimados’ se corresponden confy<-dweibull(x,2,s); nada y la estimación depweibull(c/2,2,s)*100 p es, como cabı́a esperar, mucho antes) y), en % [1] 17.82750 produce un gráfico que compara las dos funciones de densidad (la ‘verdadera’ y la ‘estimada’): > > xi<-rweibull(n,2,s); media<-mean(xi); Vxi<-var(xi)*(1-1/n); > la<-media / Vxi; wa<-media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: [1] 0.6276832 [1] 4.525886 [1] 12.35883 > fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') > > 0 5 10 15 (C) Vemos por último, para comparar sus formas, 3 densidades Gamma con distintos w (todas con factor de *** caught bus error *** escala =1), y el código que las produce. address 0x9, cause 'invalid alignment' ylab = "") 0.20 0.25 Traceback: 1: plot.new() 2: plot.default(c(x, b, x), c(fy, min(fe), fe), "l", xlab = "", 3: plot(c(x, b, x), c(fy, min(fe), fe), "l", xlab = "", ylab = "") 0.05 0.10 0.15 Possible actions: 1: abort (with core dump, if enabled) 2: normal R exit 3: exit R without saving workspace 4: exit R saving workspace Selection: Selection: 0.00 Selection: > xi<-rweibull(n,2,c); media<-mean(xi); Vxi<-var(xi)*(1-1/n); > la<-media / Vxi; wa<-media*la; la; wa; pgamma(wa/2,wa)*100 # LA ESTIMACION ERRONEA: [1] 0.7035025 0 5 10 15 [1] 4.072229 [1] 14.00203 Gamma con w = 3, 7, 11 > fe<-dgamma(x,wa,la); plot(c(x,b,x),c(fy,min(fe),fe),'l',xlab='',ylab='') > > # LA 'FORMA' DE LAS Gamma > fxw<- c(dgamma(x,3),0,dgamma(x,7),0,dgamma(x,11)) > plot(c(x,b,x,b,x),fxw,'l',xlab='Gamma con w = 3, 7, 11',ylab='') >