Problema 1 El planeta Marte, de radio R M = 3400 km rota alrededor
Anuncio

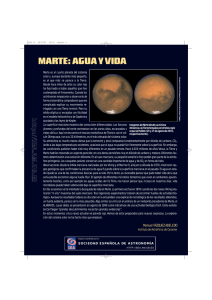
Problema 1 El planeta Marte, de radio RM = 3400 km rota alrededor del sol a lo largo de una órbita casi circular de radio rM = 2,28 · 108 km. Las medidas efectuadas por la sonda Viking I permiten afirmar que su temperatura al sol está comprendida, dependiendo de la estación, entre −20◦ C y −100◦ C. Se intentará recuperar este orden de magnitud a partir del balance térmico, suponiendo que la temperatura de Marte es uniforme. Se utilizarán los siguientes datos: el Sol radia como un cuerpo negro a TS = 5800K. la radiación solar que recibe una superficie de la Tierra, perpendicular a la dirección Sol-Tierra vale ET = 1300W m− 2 La Tierra, de radio 6400 km, gira alrededor del sol sobre una órbita de radio medio rT = 1,5 · 108 km. 1. Determinar la radiación solar EM sobre Marte en función de ET , rM y rT . (1) 2. Determinar la temperatura del suelo de Marte, TM , considerando que es un cuerpo negro calentado por el Sol. 3. Las observaciones de espectro de Viking I permitieron establecer la ley de evolución espectral del suelo del planeta rojo: eλ = ε1 = 0,8 λ ≤ 0,55µm eλ = ε2 = 0,1 0,55 ≤ λ ≤ 1µm eλ = ε1 = 1 λ ≥ 1µm Deducir: a) La absortancia total AS del suelo de Marte respecto de la radiación solar. b) La emisividad total εM del suelo de Marte. (2) c) La temperatura media de Marte, TM . 4. El valor obtenido en el punto anterior para la temperatura de Marte es inferior al valor medio experimental (−60◦ C) obtenido por Viking I. Se propone mejorar el modelo teniendo en cuenta el hecho de que, como la Tierra, Marte está constituido por un núcleo caliente de temperatura TN ≈ 2000◦ C, recubierto de una corteza de espesor δ = 5 km, de conductividad térmica k = 10W m− 1K − 1. a) Escribir la nueva ecuación de balance térmico retomando, para la radiación, los datos del punto anterior. (3) b) Deducir el valor de la temperatura promedio del suelo de Marte TM . Solución: 1. Radiación solar sobre Marte: ET A1 = EM A2 r2 Entonces EM = ET r2T M EM ≈ 563W m− 2. 2. Consideramos a Marte un cuerpo negro, La radiación efectiva que recibe es sólo función del factor de forma FSM . Para ello, asimilamos la geometrı́a al caso de una esfera (Marte) cercana a una superficie plana (Sol). Es, en este caso F12 = 1/2. Luego, considerando que sólo llega la mitad de la radiación emitida por el Sol, ES /2. EM = ES /2 · FSM = ES /4 4 En equilibrio, como Marte es un cuerpo negro, EM = σTM , σ = 5,67 · 10−8 W/m2 K 4 , luego TM = 223K = −50◦ C. a) Caracterı́sticas espectrales del suelo de Marte: Recordamos que definimos como potencia emisiva monocromática, Ebλ de una superficie negra como la energı́a radiante por unidad de área de la superficie y por unidad de longitud de onda, como define la ley de Planck: Ebλ = C1 1 5 C /λT 2 λ (e − 1) [W m−3 ] Integrando sobre todas las longitudes de onda, es posible obtener una expresión para la potencia radiantes por unidad de superficie: Z ∞ Eb = Ebλ dλ 0 El cálculo se simplifica utilizando la función fraccionaria externa fe , que puede consultarse, pej en la Tabla 6.5 pag 571 de [1]. El coeficiente de absortancia total se estima según: αtot = α1 fe (λ1 TS ) + α2 (fe (λ2 TS ) − fe (λ1 TS )) + α3 (1 − fe (λ2 TS )) Reemplazando, se obtiene αT OT = 0,57. b) En la determinación de la emisividad, se considera la temperatura propia del cuerpo. Ésta es, del primer cálculo, de aproximadamente −50◦ C. Entonces, εT OT ≈ 1. Notamos que la variación de TM alrededor de el valor anterior, no modifica este último resultado. c) La temperatura de Marte, en base a los coeficientes calculados: A partir del balance térmico, 2 2 4 αtot (πRM )ES = εT OT 4πRM EM siendo EM = σTM (2) Luego, TM = −79◦ C 3. Dado que δ RM , podemos adoptar un modelo plano. a) La continuidad del flujo térmico en la superficie de Marte nos permite asegurar: (3) (3) 2 2 2 k [TN − TM ] = εM 4πRM σ(TM )4 − αtot πRM ES 4πRM δ (3) Obtenemos el valor de TM = −76◦ C. El modelo no permite recuperar el valor medio de temperatura medido por la sonda pues no se incluyó en él la influencia de la atmósfera de Marte. Problema 2 Una construcción agrı́cola de grandes dimensiones está recubierta por un techo de tejas que forman un diedro de ángulo θ en el vértice superior. Este edificio se halla lleno de heno hasta el nivel de la base del techo, de superfice S3 . Se pide calcular la temperatura estacionaria T3 de esta superficie, considerada como adiabática, en los dos casos siguientes: 1. La radiación solar cae en forma vertical sobre el techo (sol en el cénit). 2. La radiación solar cae en forma perpendicular a un de los dos costados del techo. Se adoptan las siguientes hipótesis: La radiación solar sobre una superficie perpendicular a los rayos es: ES = 750W/m2 Todas las superficies son negras. Los intercambios de calor en el interior del techo son radiativos puros. Los intercambios de calor por convección y radiación con el exterior se resumen con la ayuda de un sólo coeficiente h = 30W/m2 K. La temperatura exterior es de T0 = 295K. La conducción t´ermica de las tejas, de espesor e = 3cm es k = 1W/mK Servirán para el primer caso, las simetrı́as de la situación. Caso 1 Por simetrı́a T1 = T2 y el factor de forma F12 = F13 = F21 = F23 = 1/2. El balance térmico en el interior del granero, sobre la cara 3, 1 1 σT34 = σT14 + σT24 (1) 2 2 Luego, T3 = T1 = T2 . El balance de calor aplicado sobre el conjunto de las dos placas del techo (1 y 2): ES S = 2hS(T10 − T0 ) (2) Como todas las caras del interior del techo se hallan a la misma temperatura, no hay transferencia de calor y, por ende, no hay gradiente de temperatura de T10 a T1 . T10 = T1 . Luego, se deduce el valor para T3 directamente de la ecuación (2). T3 = T1 = T10 = T0 + E2hS = 34,5◦ C. Caso 2 Los rayos del sol caen perpendiculares a S1 . El balance térmico en el interior es igual que en (1) 1 1 σT34 = σT14 + σT24 2 2 Sobre cada placa realizamos el balance térmico de la superficies internas y externas1 . s / Placa 1: 1 k 0 1 (T1 − T1 ) = σT14 − σT24 − σT34 e 2 2 k 0 0 (T − T1 ) = ES − h(T1 − T0 ) e 1 interior (3) exterior (4) interior (5) exterior (6) s / Placa 2: k 0 1 1 (T2 − T2 ) = σT24 − σT14 − σT34 e 2 2 k 0 0 (T − T2 ) = 0 − h(T2 − T0 ) e 2 1 Recordar que h involucra radiación y convección externas. Tenemos entonces 5 incógnitas T1 , T2 , T3 , T10 , T20 y 5 ecuaciones a resolver. Podemos hallar T3 resolviendo el sistema no lineal o bien, podemos simplificar las ecuaciones haciendo uso de una linearización de las mismas. Para ello, decimos que: Ti4 − Tj4 ' Tm3 (Ti − Tj ). En este ejemplo Tm = T0 + E2hS . Se llega entonces a que T3 ' 35◦ C. Bibliografı́a [1] Mills, Transferencia de Calor, Ed Irwin 7