LA ESTRUCTURA DEL SUBMARINO
Anuncio

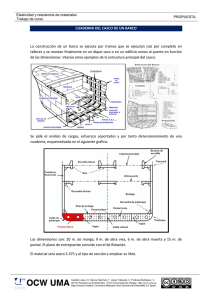
CASCO Y ESTRUCTURAS Parte 2 P. Sosa. © 03-2007 Caso 3. Anillo inicialmente ovalado Como referencia, se tiene que el anillo, supuesto totalmente circular, de 6 m de diámetro, cargado con presión uniforme exterior de 300 mca, exclusivamente, contrae su radio, de forma uniforme, 2,91 mm (5,82 mm en diámetro). Proporcional para otras presiones. En previsión de que el anillo esté inicialmente ovalado, por construcción, se va a hacer el cálculo con este ya deformado. La presión exterior se ha fijado como la correspondiente a 300 m a la parte baja del anillo (quilla), supuesto este en posición horizontal. Se ha supuesto una ovalización del 0,5% en radio, en el límite (industrial) de lo admisible, lo que representa 3000*0,005 = 15 mm de error en radio. Así que supondremos el diámetro vertical de una longitud 6030 mm y el diámetro horizontal de 5970 mm. La ovalización en este sentido es la mas perniciosa, como ya se vio ya que por la carga hidrostática base los anillos tienden a aplastarse en el sentido Br- Er. Efectuado un cálculo por separado, (utilizando una entrada de datos más perfecta en cuanto a la definición de los puntos de la elipse y la presión), para carga de presión uniforme de 294 m y una ovalización inicial, también de 15 mm en radio, el resultado es que el radio horizontal se contrae unos 8 mm (7,97 mm), (a adicionar a los 15 mm iniciales de construcción), debido a los momentos que se generan. Los resultados obtenidos para la carga combinada de hidrostática base (triangular), mas los pesos internos (peso propio del anillo mas peso distribuido en el fondo), de equilibrado del empuje que la anterior proporciona, mas la presión uniforme de 294 m (que con la triangular completan los 300 m en la quilla), se presentan a continuación, gráficamente: 35 La deformación radial (ovalización) se incrementa en 10 mm sobre la que ya llevaba de origen, 15 mm. O sea que si la presión hidrostática uniforme lo ha deformado en 2,9 mm radiales (reducción general del radio), el resto, los 7,1 mm, son debidos al efecto de los momentos producidos por la presión exterior uniforme (próximos a los 8 mm que se obtuvieron de reducción del radio en el cálculo por separado y con la misma excentricidad). El momento en el fondo del anillo, pasa de 3,76*104 N*m que había en el Caso 1, de carga hidrostática triangular y anillo totalmente circular, a 1,11*105,. Es decir se multiplica por 3 y así lo hará las tensiones debidas a la flexión, dando 965 daN/cm2 de compresión en el ala, que sumada a la esfuerzo de compresión medio por fuerza axial, (de 4,97*105 daN / 250 cm2 = 1988 daN/cm2) suponen una tensión de unos 3000 bar, en el material que forma el ala de la cuaderna, como primera aproximación. Ya veremos, mas adelante, en los capítulos que siguen, que el forro y las cuadernas no se cargan axialmente de forma uniforme. Las platabandas de las cuadernas, por estar un poco mas al interior del anillo, toman una ligeramente mayor carga axial que el forro, pero este a su vez está sometido a unas flexiones longitudinales muy fuertes (debido a la existencia de las cuadernas), por lo cual, globalmente, las cuadernas están siempre trabajando con unas tensiones (circunferenciales, uniaxiales) que son del orden del 7080% de las del forro. 36 Al ser el cálculo efectuado del tipo lineal no sabemos lo que habría ocurrido si las fuerzas de presión se hubiesen trasladado a las nuevas posiciones de la deformada. Seguramente que hubiesen producido nuevos desplazamientos, etc. Un método posible, simplificado, de obviar este problema, si no se dispone de programas que ajusten la posición de las cargas a las nuevas posiciones que va tomando la deformada es asumir que la máxima flecha de la deformada es proporcional a la ovalización inicial (sin carga). Para confirmar esta hipótesis se han calculado, a presión uniforme exterior, anillos con ovalizaciones iniciales crecientes, definidas por la reducción de su radio o semi-eje horizontal de 0, 10, 15, 25, 40, 50, 60 y 100 mm, (y un incremento equivalente del radio vertical), relativos a una circunferencia perfecta de 6 m de diámetro. Las deformaciones que se obtienen, tanto en el semieje horizontal como en el vertical, tienden a pronunciar estas ovalizaciones iniciales, como era de prever. Las elipses propuestas (con su diámetro vertical un poco mayor que le horizontal) se han achatado en el sentido horizontal, con reducción del diámetro en este mismo sentido y aumento del diámetro vertical. 37 Los resultados de esta prueba son los siguientes, para 100 mca, de presión uniforme y diversas ovalizaciones. Para 10 mca los resultados de las deformaciones hay que dividirlos por 10. Las deformaciones (movimientos) incluyen aquellas producidas por las fuerzas axiales y las producidas por los momentos flectores, combinadas. La ovalización absoluta de un anillo se va a definir de la forma siguiente, siendo a y b los semiejes vertical y horizontal respectivamente, (por convención, a>b). Ovalizació n ⇒ OOC = (a. − b) / 2 Defecto ⋅ o ⋅ exceso ⋅ de ⋅ radio ± ∆R = = (a + b ) / 2 radio ⋅ medio Rmedio Para un radio medio dado, la ovalización se puede caracterizar también por del coeficiente (a-b) / 2. En este caso particular, en carga, el radio medio puede disminuir algunos milímetros, debido a las fuerzas de compresión axial, pero como esta contracción es despreciable respecto a radio de los anillos, lo consideremos constante a efectos de cálculo de la OOC. Los resultados de estos cálculos iniciales son los siguientes, para 100 mca, de presión uniforme y diversas ovalizaciones. Para 10 mca los resultados de las deformaciones hay que dividirlos por 10. Las deformaciones (movimientos) incluyen aquellas producidas por las fuerzas axiales y las producidas por los momentos flectores, combinadas. TABLA 7.3. MOVIMIENTOS. RADIO MEDIO = 3,00 m. PRESION 100 mca. Mov. vertical punto A = 2v, Mov. horizontal punto B=u, MOVIMIENTOS hacia el centro de la elipse (+), hacia fuera de la elipse (+), RADIOS A Y B en mm en mm OVALIZACIONES 3000-3000 +0,971 -1,942 OOC =0 mm 3010-2990 +2,12 +0,357 38 OOC=10 mm 3015-2985 OOC=15 mm 3025-2975 OOC=25 mm 3040-2960 OOC=40 mm 3050-2950 OOC=50 mm 3060-2940 OOC=60 mm 3100-2900 OOC=100 mm +2,71 +1,500 +3,88 +3,774 +5,65 +7,153 +6,85 +9,38 +8,05 +11,60 +12,92 +20,28 Los movimientos de la columna derecha hay que dividirlos por 2 para obtener el movimiento del punto A, relativo al centro de la elipse. En el gráfico que sigue, construido a base de aplicar una presión uniforme de 10 mca, alrededor del anillo, con las ovalizaciones iniciales anteriores, se observa que los resultados de las deformaciones calculadas son muy coherentes entre si, y siguen trazados perfectamente lineales, por lo menos con las ovalizaciones que se estudian, que son pequeñas. En eje X se presenta la ovalización nominal, o sea la diferencia entre el los semidiámetros vertical y horizontal iniciales, de construcción, partida por dos, referida a un circulo de 3 m de radio, sin carga. E el eje Y se presentan los movimientos, relativos al centro de la elipse, de los puntos extremos de los semiejes horizontal (u) y vertical (v). En ambos ejes existe una reducción del radio local debida a la fuerza axial (compresión) mas la deformación producida por lo momentos flectores. Puede observarse, que para muy pequeñas ovalizaciones (inferiores a 10 mm) y para el escalón de carga propuesto (10 mca), el corrimiento del extremo del eje vertical es hacia adentro, debido a que el efecto de la compresión, que tiende a mover este punto hacia el interior del anillo, se impone al de la flexión, que tiene a moverlo hacia afuera. Estas líneas tienen unas pendientes y puntos de origen que aumentarán en proporción directa a la carga aplicada. Las deformadas que se presentan corresponden a una presión uniforme exterior de 10 m.c.a. para que las deformaciones sean pequeñas y se pueda asumir que se ven afectadas por las variaciones de la geometría inicial, sobre la que se calcula, con lo que los efectos no-lineales, debido al cambio de geometría, (post-carga), si existen, serán muy pequeños y despreciables. Efectivamente, p.e. para una ovalización previa de 40 mm, la ovalización total después de la carga (10 mca) es de 40+0,462 =40,462 mm, muy cercana a la anterior. Se han obtenido las ecuaciones de estas líneas, que son rectas muy bien definidas. La línea de color azul corresponde a los acortamientos del semidiámetro horizontal y la de color rojo a los alargamientos del semidiámetro vertical, bajo una presión uniforme de 10 mca, en función de la ovalización inicial. La línea de color verde, corresponde a la semisuma de los corrimientos en uno y otro eje y equivale al incremento de ovalización habido y que será la base para la integración que se efectuará para obtener los resultados no-lineales. Gráfico 1 39 DEFORMADAS (u,v) DE SEMIEJES a y b. P= 10 mca uniforme Corrimientos adicionales en los ejes, en carga (mm) 1,4 1,2 y = 0,0119 x + 0,0913 1 MOVIMIENTO SEMIEJE HORIZONTAL (HACIA DENTRO) 0,8 OVALIZACION ADICIONAL 0,6 MOVIMIENTO DEL SEMIEJE VERTICAL y = 0,01150 x 0,4 y = 0,0111 x - 0,0914 0,2 0 0 10 20 30 40 50 60 70 80 90 100 -0,2 OOC = Ovalización inicial , mm (R = Cte = 3 m) La línea de contracciones horizontales (u) corta al eje y, del gráfico a unos + 0,1 mm (0,097 mm) y el de contracciones verticales (v) en lo mismo, pero por debajo, (– 0,1 mm). Esto se justifica, en anillos totalmente circulares, (ovalización inicial cero) en que contraen uniformemente por efecto de la compresión axial, reduciéndose su diámetro. Por ese motivo el extremo del semieje horizontal se desplaza hacia la izquierda (contrae) y el semieje vertical (donde está el patín) desciende (signo negativo). El termino independiente de las ecuaciones es lo que se mueve por las contracción por compresión axial. Si se asume que el material del anillo tiene una respuesta lineal, es decir el modulo E se mantiene constante, y a cada carga adicional le corresponde una deformación, (sea cual fuera el estado inicial de carga o de tensiones del mismo), que se añade de forma algebraica a la anterior, se puede recurrir a un proceso de carga paso a paso, de 10 en 10 m.c.a. (por ejemplo), con objeto de obtener las deformaciones acumuladas, teniendo en cuenta que la deformación de un paso se acumula a la ovalización inicial y a la deformación producida por el paso anterior. Lo ideal es que estos incrementos fuesen infinitesimales, pero se estima que 30 pasos, desde 10 a unos 300 m.c.a. darán una precisión aceptable. Suponiendo una ovalización inicial de construcción de 15 mm (a = 3015 mm, b = 1985 mm), por el método directo lineal, un salto, se obtendrían, según Tabla 7.3, los siguientes movimientos, para 100 y 300 mca: Movimiento vertical Movimiento MOVIMIENTOS horizontal punto B punto A = 2v, en mm RADIOS A Y B =u, en mm OVALIZACIONES 100 mca Dmax-Dmin 3015-2985 +2,71 +1,500 OOC=15 300 mca Dmax-Dmin 3015-2985 +8,13 +4,500 OOC=15 Para 300 mca, el movimiento horizontal (u) se compone de dos componentes (ver ecuación en Gráfico nº 1, afectada por el factor 30) 1) el de compresión pura: 0,0913 *30 = 2,739 ≈ 2,74 mm 40 2) el de flexión: 0,0119 *15 *30 = 5,355 mm El movimiento total relativo, respecto ala posición inicial (+15 mm) es de 2,74+5,34 = 8,08 mm Sumados a la deformación inicial, la posición final total absoluta del punto B del eje x, después de la carga es de 15 + 8,08 = 23,08 mm. Ahora, se va a efectuar un cálculo paso a paso, de las deformaciones, hasta los 300 mca. Efectuada esta integración, utilizando ovalizaciones crecientes, l aposición absoluta total del punto B del semidiámetro horizontal, es de 24,16 mm de los que hay que descontar los 15 mm (de deformación inicial) por lo cual el corrimiento del punto B es de 9,16 mm, a comparar con los 8 mm aproximados calculados por el programa, para esta mismas condiciones de carga, pero con un solo paso. La diferencia es de un 14 % aproximadamente. Hay que observar que de estos, hay una cantidad fija que corresponde a la contracción del casco por fuerzas axiales, constante para ambos casos, (2,74 mm) por lo que la comparativa hay que hacerla entre 6,42 mm (9,16-2,74=6,42) y 5,4 mm del caso anterior. O sea, el efecto de la no-linealidad es un incremento del 19% relativo a las tensiones de flexión. Si se efectúa el cálculo con pasos de solo 2 mca el resultado para esta cota es de 24,5 mm lo cual demuestra que hay una convergencia rápida y los pasos de 10 mca dan una suficiente precisión. La diferencia es pequeña y demuestra que el impacto del incremento de la ovalización, en el cálculo de las deformaciones que se obtienen, paso a paso, es relativamente moderado. Es decir que, para estas ovalizaciones tan reducidas, la respuesta en deformación es casi lineal con la carga. Hay poca progresividad en las deformaciones. Esta baja progresión de la deformación ha ocurrido porque la inercia propuesta de la sección recta de las cuadernas es bastante grande, (21000 cm4) y, por consiguiente, las deformaciones de flexión (dependientes de EI) resultan muy moderadas. La carga crítica elástica de pandeo general (ovalización) de esta cuaderna está por los 850 m de cota, por lo cual es muy estable, muy poco reactiva. Si la inercia hubiese sido, p.e. de 1/3 de la anterior las deformaciones de flexión hubiesen sido 3 veces mayores y las pendientes de las líneas de los gráficos tres veces mayores. Hechos los números la deformación total, para los 300 mca es de unos 50 mm y descontando los 15 iniciales, resultan 35 mm de deformación pura, debida a la presión, a comparar con los 3 x 8 = 24 mm que se hubiesen obtenido por el método lineal directo, (un 45% mas). Pero a esta presión, las tensiones son excesivamente altas (axial de 1980 daN/cm2 para A = 250 cm2 mas flexión, 6150 daN/cm2) para la mayoría de los aceros normalmente utilizados. Además, de no ser así, se hubiese incurrido ya en la inestabilidad elástica (que ocurriría a los 850/3 = 283 m aprox.). El anillo no es capaz de mantener el estado de tensiones que se hubiese generado, aunque estas hubiesen sido inferiores a la de fluencia del material. En conclusión, para el rango de ovalizaciones en que nos movemos, el resultado de un cálculo lineal, respecto a las deformaciones de flexión y las tensiones correspondientes, se queda un 20 % corto, como cifra indicativa, genérica. Entrada de DATOS CASO 1. ANILLO CIRCULAR SIN CUBIERTA. CARGA HIDROSTÁTICA DE BASE 41 PARAMETROS $ par val den 1025.0 grav 9.81 k den*grav s 0.55 HQ 300 ro HA FP ang1 ang2 ang3 ang4 ang5 si1 co1 si2 co2 si3 co3 si4 co4 si5 co5 $ kg/m3 $ clara, m $ cota m quilla 3.0 HQ-2*ro k*HA*s $m $ cota m en parte alta $ fuerza radial/metro circunf. pi/12.0 2*ang1 3*ang1 4*ang1 5*ang1 $ rad $ rad $ rad $ rad $ rad 15 grados 30 45 60 75 sin(ang1) cos(ang1) sin(ang2) cos(ang2) sin(ang3) sin(ang3) sin(ang4) cos(ang4) sin(ang5) cos(ang5) PUNTOS $ pun X 0 0.0 1 0.0 2 ro*si2 3 ro*si4 4 ro 5 ro*co2 6 ro*co4 7 0.0 LINEAS $ lin tipo 1 ARC 2 ARC 3 ARC 4 ARC 5 ARC 6 ARC Y 0.0 -ro -ro*co2 -ro*co4 0.0 ro*si2 ro*si4 ro pun 012 023 034 045 056 067 MATERIALES $ mat pro 1 YOU 2.05e+11 DEN 7850.0 PROPIEDADES $ pro are iner 1 2.5e-2 21.0e-5 ELEMENTOS_LINEAS $ lin tipo mat pro 1 RIG 1 1 2 RIG 1 1 42 3 4 5 6 RIG RIG RIG RIG 1 1 1 1 1 1 1 1 DESPLAZAMIENTOS_IMPUESTOS_PUNTOS $ pun est DX DY GZ 1 1 0.0 0.0 0.0 7 1 0.0 libre 0.0 1 2 0.0 0.0 0.0 7 2 0.0 libre 0.0 CARGAS_LOCALES_LINEAS $ lin est tipo qX 1 1 PAR 0 0 0 k*ro*(1+1)*s 2 1 PAR 0 0 0 k*ro*(1+co2)*s 3 1 PAR 0 0 0 k*ro*(1+co4)*s 4 1 PAR 0 0 0 k*ro*s 5 1 PAR 0 0 0 k*ro*(1-si2)*s 6 1 PAR 0 0 0 k*ro*(1-si4)*s 1 2 3 4 5 6 2 2 2 2 2 2 UNI UNI UNI UNI UNI UNI 0 0 0 0 0 0 FP FP FP FP FP FP CARGAS_GLOBALES_LINEAS $ lin est tipo qX qY 1 1 UNI 0.0 -3.0e+4 2 1 UNI 0.0 -1.35e+4 0 0 0 0 0 0 qY k*ro*(1+co1)*s k*ro*(1+co3)*s k*ro*(1+co5)*s k*ro*(1-si1)*s k*ro*(1-si3)*s k*ro*(1-si5)*s k*ro*(1+co2)*s k*ro*(1+co4)*s k*ro*s k*ro*(1-si2)*s k*ro*(1-si4)*s 0.0 dI 0 0 0 0 0 0 dF 0 0 0 0 0 0 0 0 0 0 0 0 dI dF 0 0 0 0 CARGAS_GRAVITATORIAS $ est aX aY 1 0.0 -grav COMBINACIONES_ESTADOS_CARGAS $ estc est1 coef1 est2 coef2 3 1 1.0 2 1.0 Caso 2. Anillo circular con cubierta La entrada de datos es idéntica a la anterior (sin cubierta) con la salvedad de que se ha introducido una línea mas (POL) entre el punto 0, se ha metido un nuevo Material con sus propiedades (la barra no pesa para que no altere el balance peso-desplazamiento inicial), y se han fijada unas condiciones de contorno para esta barra (0, libre,0). Caso 3. Casco elíptico - Hidrostática elemental + P uniforme PARAMETROS $ par val den 1025.0 grav 9.81 k den*grav s 0.55 HQ 300 rv 3.015 $ kg/m3 $ clara, m $ cota m quilla $m 43 rh HA FP 2.985 HQ-2*rv k*HA*s ang1 ang2 ang3 ang4 ang5 pi/12.0 2*ang1 3*ang1 4*ang1 5*ang1 si15 co15 si30 co30 si45 co45 si60 co60 si75 co75 sin(ang1) cos(ang1) sin(ang2) cos(ang2) sin(ang3) sin(ang3) sin(ang4) cos(ang4) sin(ang5) cos(ang5) r15 r30 r45 r60 r75 $m $ cota m en parte alta $ fuerza radial/metro circunf. $ rad $ rad $ rad $ rad $ rad 15 grados 30 45 60 75 3.01296206 3.00741528 2.99988725 2.99241600 2.98698171 PUNTOS $ pun X 0 0.0 1 0.0 2 r30*si30 3 r60*si60 4 rh 5 r60*si60 6 r30*si30 7 0.0 Y 0.0 -rv -r30*co30 -r60*co60 0.0 r60*co60 r30*co30 rv LINEAS $ lin tipo pun 1 ARC 0 1 2 2 ARC 0 2 3 3 ARC 0 3 4 4 ARC 0 4 5 5 ARC 0 5 6 6 ARC 0 6 7 MATERIALES $ mat pro 1 YOU 2.05e+11 DEN 7850.0 PROPIEDADES $ pro are 1 2.5e-2 iner 21.0e-5 ELEMENTOS_LINEAS $ lin tipo mat pro 1 RIG 1 1 2 RIG 1 1 3 RIG 1 1 4 RIG 1 1 44 5 RIG 1 1 6 RIG 1 1 DESPLAZAMIENTOS_IMPUESTOS_PUNTOS $ pun est DX DY GZ 1 1 0.0 0.0 0.0 7 1 0.0 libre 0.0 1 2 0.0 0.0 0.0 7 2 0.0 libre 0.0 CARGAS_LOCALES_LINEAS $ lin est tipo qX 1 1 PAR 0 0 0 k*rv*(1+1)*s 2 1 PAR 0 0 0 k*r30*(1+co30)*s 3 1 PAR 0 0 0 k*r60*(1+co60)*s 4 1 PAR 0 0 0 k*rv*s 5 1 PAR 0 0 0 k*r60*(1-si30)*s 6 1 PAR 0 0 0 k*r30*(1-si60)*s 1 2 3 4 5 6 2 2 2 2 2 2 UNI UNI UNI UNI UNI UNI 0 0 0 0 0 0 qY dI dF k*r15*(1+co15)*s k*r30*(1+co30)*s 0 0 k*r45*(1+co45)*s k*r60*(1+co60)*s 0 0 k*r75*(1+co75)*s k*rh*s 0 0 k*r75*(1-si15)*s k*r60*(1-si30)*s 0 0 k*r45*(1-si45)*s k*r30*(1-si60)*s 0 0 k*r15*(1-si75)*s 0.0 0 0 FP FP FP FP FP FP CARGAS_GLOBALES_LINEAS $ lin est tipo qX qY 1 1 UNI 0.0 -3.0e+4 2 1 UNI 0.0 -1.35e+4 0 0 0 0 0 0 0 0 0 0 0 0 dI dF 0 0 0 0 CARGAS_GRAVITATORIAS $ est aX aY 1 0.0 -grav COMBINACIONES_ESTADOS_CARGAS $ estc est1 coef1 est2 coef2 3 1 1.0 2 1.0 7.4.- Tipos de Fallo 7.4.1.- Introducción Los cascos de los submarinos representan actualmente las estructuras soldadas más grandes que existen, resistentes a la presión. Independientemente de sus dimensiones, estas estructuras reúnen características peculiares tanto en la concepción como en las tecnologías empleadas. El margen de seguridad, muy reducido, con que están dotadas, si se tiene en cuenta los efectos dinámicos, el choque a que pueden estar expuestas y la gran agresividad del agua de mar, necesita una gran precisión en el cálculo de los esfuerzos y sus diferentes modos de fallo así como una ejecución muy cuidada de los elementos que las integran. En la actualidad, el coeficiente de seguridad para la estructura completa oscila de 1,65 a 2, para profundidades moderadas. Un coeficiente tan pequeño obliga a conocer perfectamente como se produce la rotura o ruina de la estructura, a qué cargas y de que forma, con el fin de asegurar su integridad en las condiciones normales de trabajo. El margen de seguridad tan bajo obedece a la necesidad de ahorrar peso para equipos, propulsión etc., sin los cuales el submarino poseería una cualidades operativas mas reducidas y quizás inaceptables o en franca desventaja con sus competidores. Independientemente de la calidad de los materiales empleados y exceptuando aquellos fallos producidos por agrietamiento del material por no reunir las características de 45 ductilidad necesarias, por defectos internos locales o defectos de soldadura y todos aquellos derivados de procesos tecnológicos inadecuados, los fallos por los que un casco resistente se destruye son, fundamentalmente, los que se describen a continuación. Se entiende como "fallo" el modo en que la estructura deja de ser útil para los fines a que se destina, es decir, mantener su capacidad resistente, aunque no suponga realmente un "fallo" en el sentido de equivocación o defecto de cálculo del dimensionamiento. En muchos casos, los fallos, que pueden ser de naturaleza diversa, no se producen de forma singular o independiente, de fácil identificación sino que, una vez comenzado uno de ellos, cualquiera otro de los restantes modos o todos ellos simultáneamente, pueden verse afectados, provocados, anticipados, mezclándose con el inicial. A efectos teóricos, evidentemente, puede tener mucho interés el estudio de las interacciones, pero una vez iniciado cualquier tipo de fallo, ya no tiene importancia, a título práctico, conocer si se ha producido algún otro simultáneamente o con cierto desfase puesto que la estructura ya se debe dar por perdida, Lo que si debe ser estudiado con todo detalle son las interacciones entre los diferentes modos de fallo, en el comportamiento de la estructura, antes de que cualquiera de ellos se produzca. Es decir la posibilidad de un fallo combinado, provocado por la acción de los más susceptibles aunque no se llegase teóricamente a la ruina con ninguno de ellos tomados de forma independiente. Esto suele ocurrir cuando las presiones calculadas de fallo de dos o mas modos están muy próximas. Por este motivo es conveniente que las presiones calculadas de fallo en cada uno de los modos estén separadas lo mas posible y no se interfieran entre si y no afecten demasiado el modo mas propenso a ocurrir. Es necesario, por consiguiente, asegurarse de que la estructura inicie el fallo de un solo modo o que la interacción de los probables esté perfectamente controlada. Afortunadamente, se dispone de numerosos resultados experimentales que permiten establecer ciertas reglas prácticas de interacción aunque su cálculo teórico sea aún un asunto bastante confuso e impreciso. Hasta hace pocos años se tenia la certeza de que aquellas estructuras que gozaban de menor peso, es decir las mas eficientes, eran las que se caracterizaban por tener todos los modos de fallo situados a una misma presión, ligeramente superior a la de cálculo, quizá bajo la influencia del razonamiento de que así el material, la estructura, estaría trabajando al máximo en todas sus facetas, en todos sus modos. Sin embargo, en la actualidad se ha demostrado que esto no es cierto. Se pueden conseguir estructuras que, dando el peso mínimo, posean modos de fallo muy alejados de la mínima presión teórica, es decir, que fallan de un solo modo bien diferenciado y el resto pude estar disperso a presiones criticas mas altas. Ello es debido básicamente, a que muchos de los modos de fallo consisten en inestabilidades estructurales que no dependen de las características mecánicas del material utilizado sino del dimensionamiento geométrico y de la armonía de proporciones de los elementos integrantes de la estructura, junto con el módulo E del material. En realidad la llamada armonía de proporciones equivale a coordinar perfectamente las medidas de las claras entre cuadernas respecto al espesor del forro, el valor de la anchura respecto al espesor de almas de refuerzos, etc. Los fallos que se describen a continuación se refieren a estructuras solicitadas estáticamente. Pueden aparecer fallos distintos en estructuras sometidas a cargas dinámicas, tales como explosiones cercanas, colisiones o golpes de mar, que suelen producir abolladuras o desgarramientos más o menos localizados, de características muy variadas. Asimismo, por efecto de la fatiga del material pueden aparecer grietas o fisuras en ciertas zonas muy cargadas de la estructura (concentración de tensiones) que no son contempladas como fallos estructurales sino del material, por lo cual no las incluimos en el concepto de los fallos que estamos tratando. Como estructuras, se consideran básicamente cilindros y conos de baja apertura reforzados por cuadernas y domos de diversos tipos. 46 De los posibles tipos de cuadernas se van a considerar básicamente las formadas por una T, o sea compuestas por un alma y una platabanda soldada esta, con el por el lado libre del alma soldada al forro que se pretende reforzar. Este tipo de cuaderna es el mas adecuado ya que permite el acceso fácil al cordón de soldadura del alma al forro, no tiene zonas ocultas (como pasaría en una cuaderna en U) por lo que la inspección es mas fácil, y es la mas sencilla de construir. Las cuadernas trabajan asociadas al forro, y como en cualquier buque, existe un ancho efectivo de este para el cálculo de la inercia combinada. Con el objeto de obtener grandes inercias combinadas, es decir una mayor capacidad de absorber esfuerzos flectores, las platabandas deberán estar lo mas alejadas que ello sea posible del forro, lo cual implica almas de una altura respetable. Asimismo, el área de la sección recta de las platabandas conviene que sea también alta. Ambos elementos, alma y platabanda, se suelen construir a base de pletinas gruesas soldadas entre si, o bien a base de laminados específicos en forma de T, aunque, al ser de materiales poco comerciales y geométricamente fuera de norma, la laminación de una cuaderna completa es un método costoso y poco usual. Los fallos más comunes de un recinto reforzado por cuadernas, sometido a presión exterior, se pueden clasificar en tres tipos, a efectos analíticos: 1) Fallos que afectan exclusivamente a las cuadernas 2) Fallos que afectan al forro 3) Fallos de la estructura completa o de inestabilidad del tipo general Deslindar estos fallos es por simplificar, ya que cuando las cuadernas o el forro se deforman, aunque sean por motivos claramente achacables a cada uno de estos elementos, siempre queda afectado o involucrado, de alguna manera, el elemento colindante, íntimamente unido a el. En todos ellos, aunque el origen se concrete en alguno (o varios simultáneamente) de los fallos anteriormente citados, se produce, a la postre, un colapso generalizado que produce la ruina total de la estructura. En los Apartados que siguen mas adelante, (Apdos. 7. 19 y siguientes) se analizarán todos estos fallos con mayor precisión, de forma numérica, las tensiones que los producen, etc. pero, por el momento se presentan estos, de forma ilustrativa, para ir familiarizando al lector con los modos en que los cascos (resistentes) de los submarinos colapsan y se destruyen. 7.4.2.- Fallo por inestabilidad de las cuadernas Las cuadernas, tomadas en conjunto con el forro, por estar soldadas a este, no pueden colapsar o deformarse independientemente y separadamente de el, sobre todo cuando se consideran anillos macizos de una sección muy compacta, del tipo que se muestra en la figura de más abajo. Pero las cuadernas reales están formadas por perfiles esbeltos y abiertos que pueden adolecer de un dimensionamiento incorrecto de sus elementos integrantes, ala y alma, y estos sí pueden estar expuestos a deformaciones locales, inadmisibles, que pueden ser el origen de fallos generales. 47 Como consecuencia se deberán respetar unos criterios de dimensionamiento para evitar que, con el afán de reducir peso, se obtengan almas o alas muy esbeltas y expuestas a deformaciones o alabeos prematuros que pudieran acarrear la perdida de su capacidad resistente provocando el fallo total de la estructura. Las cuadernas pueden estar situadas por el interior o el exterior del casco resistente. A efectos de pandeo o inestabilidad, las situadas por el exterior son un poco más estables, por su forma de trabajar. En estas, el forro del casco, al reducir su radio por efecto de la presión exterior, tira radialmente hacia dentro del alma de la cuaderna y esta, a su vez lo hace del ala, obligándola a reducir su radio. En todos los casos, estos elementos están sometidos a una tensión circunferencial que los comprime en el sentido transversal pero las almas, en las cuadernas exteriores, están sometidas a una cierta tracción radial lo que les proporciona una mejora de su estabilidad. En las exteriores, es difícil que las cuadernas como conjunto se plieguen o se vuelquen sobre el forro del casco, ya que estas tienden a separarse del el. Por el contrario, las almas de las cuadernas interiores empujan el casco hacia afuera, apoyadas y respaldadas por las alas, que son flotantes, y que tenderán a ladearse o tumbarse para descomprimirse. Por ser las cuadernas elementos muy básicos e importantes, sobre los que se apoya el forro formando una unidad con estas, es necesario aplicar criterios muy conservadores de resistencia y estabilidad. Además, por representar una parte relativamente pequeña del peso total, un ligero sobredimensionamiento no supone una gran penalización en el peso. En lo que sigue nos referiremos a cuadernas situadas por el interior del casco resistente. Si están por el exterior el dimensionamiento es similar, aunque son un poco mas estables “per se”. Puesto que las cuaderna (en T) se componen solo de dos piezas que son el ala (o platabanda) y el alma, el criterio mas extendido y mas seguro para el dimensionamiento de estos elementos es el de establecer unas relaciones máximas entre anchura y espesor (en alas) y entre la altura y espesor en almas, para cada acero (o material) considerado. Los fallos más comunes que aparecen en las cuadernas son los siguientes. Ver Fig. nº 14. 1. Abolladura del alma, en almas de espesor reducido, (tipo 1) 2. Alabeo del ala, (tipo 2). 3. Pandeo de las cuadernas como conjunto, (tipo 3). Los fallos del tipo 1 y 2 corresponden a la inestabilidad de las almas o las alas tomadas de forma independiente. Es decir su prueba consistiría en sujetarlas firmemente a unas guías, por separado, y someterlas a compresión (que puede asimilarse a una compresión de barras o placas largas), siguiendo su directriz. Las almas y alas aunque son de forma circular, puesto que su radio es muy grande comparado con su anchura y espesor, 48 relativamente, se pueden tratar como placas planas de cantos rectos, es decir rectangulares. Las placas (tiras de material) de las almas se suponen colocadas en dos guías muy fuertes, una en cada borde, que les permiten resbalar longitudinalmente y girar en los bordes, transversalmente. Si se someten a unas cargas axiales crecientes, (simulando la compresión que estas soportan cuando forman el anillo cerrado), llega un momento que las almas empiezan a abollarse por el centro, alternativamente a un lado y a otro, entre las dos guías, formando unas ondas longitudinales, aunque los bordes sigan rectos, a causa de que están firmemente sujetos por las guías. Lo mismo se puede aplicar a las alas, con la salvedad de que solo se tendrían una guía, central, que impediría que la línea central del ala se curvase. Se deformarían en forma de festón Estos pandeos se ven favorecidos si el montaje de las cuadernas sobre el casco no está bien hecho. En la figura anexa se presentan las tolerancias que se emplean, con carácter general, en el montaje y posicionamiento de las cuadernas, que deberán respetarse una vez soldadas. Estas tolerancias varían de acuerdo con las instrucciones técnicas de cada Reglamento o Norma y pueden ser modificadas en función de las hipótesis de cálculo de las mismas. Pandeo del alma de las cuadernas Las almas pueden ser propensas a abollarse. La abolladura del alma (tipo 1) se produce en almas de muy poco espesor comparado con su altura. Consiste en una serie de abolladuras alternadas (para un lado y otro del plano del alma) que corren a lo largo del alma de la cuaderna, en sentido perimetral. Las almas y alas están sometidas a compresión pura en sentido circunferencial, siendo pequeños los efectos debidos a la eventual flexión, a la fuerza cortante y a la tensión radial. Para poder aprovechar al máximo las almas, será necesario que puedan soportar, sin deformarse, las cargas exteriores que se apliquen (en borde de la cuaderna, procedentes del forro) hasta que estas lleguen al límite de fluencia. Cuando decimos deformarse nos referimos a deformarse fuera de su plano porque, evidentemente, todo material sometido a tensiones se deforma. La deformación dentro de su plano es inevitable (correspondiente a una compresión pura) pero no entraña peligro dando lugar solo a una reducción del radio medio de la cuaderna, manteniendo su forma circular. La tensión crítica teórica de abolladura, de un alma, en régimen elástico, es: σcrítica ⋅ (elástica ) = σ cr = K * π 2E ⎡ espesor ⋅ del ⋅ alma ⎤ ∗⎢ ⎥ 2 12 ⋅ (1 − ν ) ⎣ altura ⋅ del ⋅ alma ⎦ 49 2 Esta expresión es una generalización de la utilizada para placas apoyadas o empotradas en sus bordes comprimidas en su plano. El alma se considera apoyada en el forro y en la platabanda, si la lleva. El valor de K varía de 0,59 para cuadernas desprovistas de ala, a 4,0 para cuadernas con platabanda o ala muy robusta. Esta platabanda deberá reunir unos requisitos mínimos para que pueda considerarse como apoyo efectivo. Su dimensionamiento se considerará en los apartados que siguen. A esta tensión crítica teórica es necesario aplicarle unos coeficientes reductores experimentales para tener en cuenta las pequeñas distorsiones iniciales de la plancha, las tensiones internas, las inexactitudes del montaje, etc. cuyo valor es de 2 a 2,5, y que designamos por el factor gamma (γ) Para que no aparezca abolladura antes de que el alma alcance el límite de fluencia se deberá tener entonces que, siendo σ y la tensión de fluencia del material utilizado. 50 σ cr (régimen elástico) >> σ y En cuadernas con platabanda, K = 4,0, resultando: γ⋅ dw π ≤ tw 3 E ⋅ (1 − ν 2 ⋅ 1 σy donde dw = altura del alma tw = espesor del alma 6 Para E =2,05 • 10 bar, … ν = 0,3… y …..γ = 2, resulta: dw 2690 1345 ≤ ≅ tw γ ⋅ σ y σy (4-1) σy = tensión de fluencia del material, en bar Se observa que cuanto mayor el límite de fluencia del material que forma la cuaderna, menor es la esbeltez admisible para el alma, definida como el cociente dw/tw o relación altura / espesor (o anchura de la tira de plancha que forma el alma y su espesor). Por ejemplo, para un acero con un limite de fluencia de 6900 bar, la relación altura/espesor de alma admisible sería de 16,25. Se podría subir hasta dw/tw = 18, si se tiene en cuenta que los cordones de soldadura ocupan algo del altura del alma quedando una menor altura libre efectiva de la misma, o a base de reducir algo el factor de seguridad. Si se tiene un alma de 12 mm de espesor, la altura libre admisible sería de unos 12 *16,25 mm = 195 mm, mas unos 20 mm de soladura (cordones alma-forro y alma-ala) darían una altura admisible máxima del alma de unos 215 mm. En construcción civil este valor (dw/tw) es del orden de 40, aunque, en submarinos, la compresión axial suele ser mucho mayor. Lo mismo se puede decir para el ala. Para que el ala pueda considerarse apoyo efectivo es necesario que su anchura cumpla lo siguiente, df ≥ 0,50 ⋅ ( dw + tf / 2) (4-2) donde df = la anchura total del ala, de borde a borde y tf su espesor. En general las almas cumples este requisito sobradamente porque se suelen construir poco esbeltas, o sea, muy compactas. En esencia lo anterior equivale a afirmar que la anchura del ala sea mayor que el 55 % de la altura del alma que rigidiza. Esto corresponde a alas con el mismo espesor que el alma. Para alas de mayor espesor este % puede reducirse algo, aunque no sea esto conveniente. Esta relación de anchuras es la comúnmente utilizada en las estructuras industriales de acero rigidizadas por refuerzos de borde o labios, por lo que su efectividad está avalada por la práctica. La relación anchura del ala / altura del alma (df/dw) suele ser del 0,5 al 0,75. Este valor en la construcción civil oscila entre un 0,5 y 1.0 51 Pandeo del ala de las cuadernas Cuando una cuaderna se somete a fuerzas radiales, las almas transmiten a sus alas o platabandas parte de estas fuerzas radiales, tomando estas últimas tensiones circunferenciales. Puesto que las alas no tienen un soportado lateral, solo la soldadura que las une sus almas, tienden a zafarse de las tensiones mediante alabeo de sus bordes en forma de sinusoide o volcando. Para que el borde libre de las alas no se alabee por efecto de la compresión circunferencial a la que están sometidas, es necesario que la relación anchura /espesor de estas no supere el valor siguiente, (K = 0.5). γ⋅ Para, E = 2,05 • 106 bar…. π df E 1 ≤ ⋅ ⋅ tf 6 1− ν 2 σy (4-3) ν = 0,3 … y γ = 3 df 1901 800 ≤ ≅ tf γ ⋅ σy σy 4-4) siendo: df = altura del ala (flange) tf = espesor del ala El alabeo a que nos referimos consiste en un giro alternativo, con torsión, del ala respecto a su posición original. En resumen, en el dimensionamiento, de las cuadernas se tendrá en cuenta las siguientes normas: 1) Evitar pandeo individual del alma: 2) Estabilizar la cuaderna, total: 3) Evitar pandeo individual del ala: dw 1345 ≤ tw σy df ≥ 0,50 ∗ ( dw + tf / 2) df 800 ≤ tf σy (4-5a) (4-5b) (4-5c) Existe una cuarta condición práctica que es la siguiente, a efectos de aumentar la inercia de la cuaderna todo lo posible, y la compacidad del ala: 4) Espesor conveniente del ala: tf > 2 tw (4-5d) El espesor del ala, tf, suele ser igual al espesor del forro, por cuestiones constructivas, o un poco mayor para maximizar la inercia. Por consiguiente, para cuadernas en T en acero HY~100, de unos 69 hbar de límite de fluencia, tendríamos las siguientes relaciones dimensionales 1) 3) 2) 4) alma = > altura /espesor < 16,2 ==>>>> 18 anchura ala > 55 % altura de alma (o > 50% de la altura total de la cuaderna) ala = > anchura /espesor < 9,6 espesor ala > 2 * espesor alma ······ => espesor de forro (por eficacia) 52 En la práctica se pueden aumentar ligeramente estas relaciones de esbeltez, ya que las zonas soldadas del alma y ala, por ser más gruesas, no deberían contarse. Así, a un alma de 220 mm de altura deberían descontarse 10+10 =20 mm del espesor medio de los cordones que la sujetan al forro y al ala, para obtener su altura “libre”. Es necesario señalar que los valores aquí recomendados coinciden prácticamente por los dados por la norma BS 5500 y otros Códigos, ya que su origen es puramente matemático, derivados de la resistencia de materiales, comprobados y validados experimentalmente y, por consiguiente, aceptados universalmente. Así, para una cuaderna de un alma de 200 mm de altura (incl. soldaduras), en acero HY100, se tendrán los siguientes valores límites (límites mínimos o máximos en cada caso): dw neta = altura de referencia: 180 mm, aprox. (altura real 200 mm) tw => dw/16,25 => 11,08 mm… (5,54 % de la altura total) df = > (50% dw bruta ) => 100 mm (mínimo) tf = > 100/9,6 => 10,5 mm (10,5% de df mínimo) por inestabilidad propia tf = > 2 * tw = 24 mm (por eficacia) Esto no quiere decir que las cuadernas óptimas, desde el punto resistente del anillo sobre el que van soldadas, deban ser así. Por ejemplo una cuaderna bastante común en sus proporciones, para el HY100, (69 hbar), es la que tiene, tomando como referencia la altura del alma, dw: - un espesor de alma del orden de 6,5 al 7% de dw una anchura de ala (df) que es el 60-70 % de dw un espesor de ala (tf) del orden del 20%-25% de df, (o similar al espesor de forro) Una cuaderna real típica, para un casco de unos 6 m de diámetro y una cota de destrucción de unos 600 sería la siguiente, (HY 100): o o o o altura del alma: espesor del alma: espesor de platabanda : anchura de platabanda: 180-210 mm 12-14 mm 30 a 35 mm 125 a 150 mm Se suele apurar mucho con la relación altura / espesor de alma, es decir se diseñan almas del menor espesor posible, para beneficiar la inercia de las cuadernas con un peso reducido del sus almas (reciben fuerzas cortantes reducidas). La anchura del ala se suele también ajustar mucho, (a base de aumentar su grosor) para poder aprovechar mejor el espacio entre las cuadernas. Estas recomendaciones se pueden generalizar para otros tipos de cuadernas. Para cuadernas sin platabanda, es decir formadas por una simple pletina circular soldada al forro, o con un pequeño bulbo, mucho menos estables que las de T, que solo se utilizan en recipientes muy pequeños, se deberá cumplir: dw / tw ≤ 1000 / σ y Para este mismo tipo de cuadernas, pero punteadas al forro y con cierta libertad de giro respecto a este, se debe tener, 650 dw / tw ≤ σy 53 Pandeo de las cuadernas tomadas como un conjunto ala-alma Es evidente que, cuanto mas altas sean las cuadernas, menor sea el espesor del alma y menor la anchura del ala, las cuadernas van a ser mas esbeltas y menos estables. Con la relación anchura/espesor del ala no hay problemas ya que las alas suelen ser bastante compactas, es decir relativamente compactas por motivos resistentes (inercia). Existen varias formas de inestabilidad o de fallo que corresponden al fallo de la cuaderna como conjunto ala-alma, aunque raramente ocurren si se dimensionan según las recomendaciones anteriores. No obstante es conveniente comprobar si es posible su aparición a pesar del dimensionamiento prescrito. Estas formas o modos son: Modo 1: Pandeo lateral de la cuaderna completa, formando ondas, alternativamente hacia un costado y hacia el otro, de su plano, (nº de ondas >1). Modo2: Desplazamiento uniforme del ala de la cuaderna hacia un costado (Tipo 3). El ala de la cuaderna se desplaza hacia proa o popa, (n = 0) en toda su longitud. Modo 1: En este modo, las cuadernas se inclinan alternativamente a un lado y a otro del pié de cuaderna, haciendo una especie de ondulación circunferencial, para así conseguir rebajar su carga axial. Rechazan su puesta en carga. El modo 1 es equivalente al que ocurre en perfiles abiertos rectos con uno de sus bordes guiado (el pié de cuaderna) o sujeto a un soporte recto indeformable, sometidos a una presión axial. Este modo de fallo se suprime dándole al ala de las cuadernas una cierta anchura mínima; la platabanda toma así la configuración de cilindro corto y esto evita que pueda girar y retorcerse, por sectores. Es decir, debe tener una cierta inercia transversal mínima (= inercia de su sección recta respecto a un eje en dirección radial pasando por el centro geométrico del ala). Esto se traduce en que cuanto mas ancha es el ala, respecto ala altura de la cuaderna, mejor. La tensión crítica de pandeo lateral, en régimen elástico, para este modo, es: σ cr = Siendo, Is A Rg d E ⋅ Is ≥ σy A ⋅ Rg d (4-6) inercia de la cuaderna respecto a su eje de simetría (línea radial) área de sección recta de la cuaderna radio de su centro de gravedad distancia del forro (pié de cuaderna) al centro de gravedad de la cuaderna aislada (sin considerar forro asociado) En esta expresión se supone que la cuaderna puede girar libremente respecto el forro, en su punto de contacto (pié de cuaderna). Bajo compresión axial, la cuaderna se inclina a un lado y a otro, alternativamente, con una torsión. Al estar soldada, es decir empotrada en el forro, el giro se ve dificultado y con esta fórmula se obtienen resultados conservadores. Esta tensión crítica deberá ser mayor que el límite elástico del material para conseguir que la cuaderna pueda absorber toda la carga posible sin ladearse o retorcerse. En general, esta condición equivale a la expuesta en la expresión (4-5b), aunque esta última sea más sencilla. En la mayor parte de de los casos la expresión (4-6) es excesivamente exigente y puede conducir a un sobredimensionamiento del ala, aunque puede servir de referencia. No se conocen expresiones sencillas para el caso real, de cuadernas soldadas, por lo que si desea más exactitud es necesario el cálculo específico de este modo de pandeo. El método a aplicar figura en la Ref. nº 56. 54 Modo 2: Cuando, por defecto de montaje, las cuadernas no se sitúan perfectamente perpendiculares al forro, en toda la circunferencia, la reacción radial, hacia fuera, del ala de la cuaderna, al no estar en el plano del alma, produce una compresión y un momento flector lateral que puede doblar (potencialmente)el alma hacia un mismo lado, (deformación tipo 3, de la Fig. 14). El ala apenas se alabea, permanece paralela al forro, al ser un cilindro corto. La rigidez de la cuaderna, en el sentido radial, disminuye algo y por consiguiente, su reacción sobre el forro también, equivaliendo, a cuadernas de una menor sección o robustez (menor coeficiente K de rigidez). El alma hace algo de muelle, especto al ala. Un control regular de la perpendicularidad (escuadría, en términos navales) de las cuadernas sobre el forro, durante el montaje y soldadura, permite evitar este fenómeno. Se estima que una falta de perpendicularidad inferior a 1 grado es totalmente permisible (industrialmente hasta 2º). En el Apartado correspondiente a las tensiones en las cuadernas se muestra el cálculo de la reacción radial del ala sobre el alma que nos permite la obtención de las fuerzas y momentos radiales que actúan sobre una cuaderna, procedentes del forro. Aparte de estos requerimientos, relativos exclusivamente a cuestiones estructurales primarias, conviene dar a las almas algunos mm de sobre-espesor (ya que este es relativamente pequeño en comparación con el forro), para mejorar algunos aspectos de la soldabilidad; para compensar las fuerzas laterales producidas por la presión de los fluidos contenidos en los tanques, cuando las cuadernas se incorporan a los mamparos que sirven de cierre de estos, por proa o por popa; para compensar la posible corrosión en sentinas; compensación de los orificios de desagüe, groeras, etc. (hay que evitar estos orificios al máximo y realizarlos con esmero, sin entallas, etc.) Por ser difícil, en la práctica, obtener un posicionamiento perfecto de las almas respecto al forro, sobre todo teniendo en cuenta que, durante la soldadura hay deformaciones angulares, las cuadernas se tumban por el lado por el que están siendo soldadas, conveniente que el área del ala no sea excesivamente grande respecto a la del alma, para evitar que una gran reacción del ala sobre un alma (muy justa de espesor), con cierta inclinación, pueda sobrecargarla (es como empujar con un cilindro hidráulico una chapa de canto). Se recomienda la siguiente relación, area ⋅ del ⋅ ala E R 1 ≤ ⋅ ⋅ area ⋅ del ⋅ alma 3000 dw σ y (4-7) Toda esta formulación gira sobre le mismo fenómeno, pero viéndolo desde varios ángulos, y que es la estabilidad del alma/ala cuando el ala aprieta sobre el alma. Se deduce de esta expresión que cuanto mayor sea la altura de la cuaderna y mayor el limite elástico del material utilizado (ya que se pueden trasmitir mayores cargas sin superarlo), menores deben ser las relaciones área del ala / área del alma. No obstante, los requerimientos de esta ecuación no se oponen a los anteriores, aunque los restringen, permitiendo poder montar alas de secciones rectas 1,5 a 1,8 veces mayores que las almas, en aceros de hasta 60 hbar de límite elástico y relaciones radio del anillo/altura de cuaderna de 14. En aceros de más alto límite de fluencia, el HY100, HY130, o sus equivalentes el 80HLES y el 100 HLES se aplicarán las mismas fórmulas, que se convierten en requisitos más restrictivos, a efectos de tener una alta inercia del perfil, pero aun aceptables. Además, como las platabandas de las cuaderna nunca llegan a cargarse al 100 % del limite de fluencia (antes lo hace el forro), esta relación se puede aumentar en un 20%, aproximadamente. Los perfiles comerciales, barras rectas, (IPN, IPE, etc.) pueden dar una idea de las proporciones relativas de los dos elementos que componen una cuaderna. Las alas comprimidas de estos perfiles, en montajes corrientes responden unas solicitaciones parecidas. No obstante, en la mayor parte de los casos estos perfiles están sometidos a flexiones que varían a lo largo de su longitud, con unas alas comprimidas y otras 55 extendidas que sirven como elemento estabilizador, o están arriostradas, o insertadas en cubiertas rígidas, por lo cual el problema de la inestabilidad es mas liviano, comparado con la forma de trabajo del alma del ala o de una cuaderna completa, que no van arriostrados. Se ha sugerido que, para evitar que las cuadernas vuelquen o se desplacen hacia un costado, se podrían poner entre las cabezas de estas, en sentido de la eslora del buque, contretes o distanciadores que la mantuviesen todas paralelas (no es de prever un movimiento de todas ellas al mismo tiempo hacia el mismo costado). Este sistema ha demostrado que es inadecuado, ya que el casco contrae longitudinalmente. La contracción longitudinal, para un submarino en el entorno en que nos movemos, es del orden de 0,6 mm / metro (a 600 m de cota). Esto supone una contracción de 6 mm en 10 metros, por lo que las cuadernas situadas a esta distancia de un origen fijo, se verían empujadas hacia un lado, u otro, por la presión de los contretes o presillas, (que no toman carga longitudinal de origen hidrostático), lo cual no es admisible desde el punto de vista de las tensiones, en el pié de las cuadernas, ni de la fatiga. En resumen, al casco hay que dejarlo “respirar”. Hay un problema de este tipo que se plantea con los soportes grandes de abordo, soldados a varias cuadernas consecutivas, los tanques de combustible, etc. que crean impedimentos a libre juego de estos refuerzos (expansión o desplazamiento de los mismos de acuerdo con las dilataciones del casco). Todo lo anteriormente descrito se aplica a cuadernas en forma de T con el alma en el eje de simetría. Un tipo de cuaderna menos corriente es la del tipo U que, soldadas al forro, forman un cajón y por ello se las denomina, a veces “de cajón". Esta clase de cuadernas tiene la ventaja de que son muy estables al no estar expuestas a pandeo lateral, inestabilidad del ala o flexión lateral. Solo pueden estar expuestas a la abolladura de sus almas o alas. Tienen además la ventaja de que reducen la clara o el vano libre del forro entre cuadernas, por se mas anchas. Su peso suele ser más elevado que el correspondiente a cuadernas en T (por llevar dos almas) y son de una construcción más laboriosa. Tienen el defecto fundamental de que su soldadura al forro no se puede revisar por dentro y quedan zonas ocultas a la vista, dentro del cajón, de difícil inspección por lo cual que si hay una corrosión imprevista, por fisura del forro, etc. o una entrada de agua (por las groeras), es difícil de detectar, lo cual es inadmisible en un submarino. Si las cuadernas se sitúan por el exterior, del tipo que fuese, se obtiene mas estabilidad, al estar el alma a tracción en sentido radial aunque su rigidez axial, por ser su radio medio mas grande, es menor que las situadas por el Interior. Estas están expuestas a mayor corrosión siendo necesario un ligero aumento de espesores y por este motivo las posibles ventajas se anulan. La corrosión de su soldadura al forro puede desprender las cuadernas dejando desprovisto al forro de su reforzado, sin poderse advertir, (la inspección visual nunca es completa por la gran cantidad de obstáculos que hay junto a las cuadernas), cosa que no ocurre en las interiores que pueden ir incluso punteadas (aunque no es admisible en submarinos militares, por la posibilidad de que los puntos, si se agrietan afecten al forro) ya que su forma normal de trabajo las oprime contra el forro. En general, cuando un anillo con sus cuadernas pandea, las cuadernas resultan deformadas en alto grado y es difícil determinar el modo de pandeo que ha provocado el colapso, si ha sido por culpa de las cuadernas, que han fallado prematuramente o del forro que las ha arrastrado y deformado de forma aleatoria. En las pruebas de cilindros reforzados, en tanques de presión, al objeto de poder dilucidar el modo de pandeo inicial, se suspende la prueba (es decir se anula o rebaja la presión exterior) justo en cuanto se detecta una disminución determinada del volumen del casco que se prueba, lo cual es síntoma del comienzo de colapso. Se obtiene así un proceso de pandeo “a cámara lenta”, pero aún así es preciso un análisis detallado de todos los factores que intervienen. 7.4.3. Fallo por plastificación del forro 56 En ensayos con modelos de recipientes a presión construidos a escala, la geometría a probar es la misma que la natural afectada del factor de escala, pero la presión de prueba y las características mecánicas del material son las mismas que las reales, sin afectar por ningún factor. Esto se deriva de las relaciones de presión, tensión y geometría aplicables a estos recintos. En la formula general de anillos y cilindros sometidos a presión se tiene que, Tensión ⋅ circunferencial ⇒ σ θ = p⋅r t Siendo p la presión, r el radio del recinto y t el espesor de pared. Resulta que para r y t a una misma escala, los valores de σ y p no se ven alterados. Esta ley se puede generalizar para cualquier forma de recinto o estructura de paredes delgadas, sometida a presión. El fallo, por plastificación, como su nombre indica, se produce por la plastificación local de la plancha que forma el recinto resistente o forro del casco de presión. Cuando las cargas hidrostáticas se van elevando, las tensiones que el material soporta lo hacen igualmente, de forma casi proporcional. Llega un momento en que se alcanza el límite proporcional de elasticidad del material en algún punto o zona de la estructura. Si se continúa aumentando las cargas se puede llegar al límite de fluencia y cuando las zonas en este régimen son lo suficientemente amplias, (el modulo de elasticidad que gobierna es el módulo tangente, mucho mas pequeño que el inicial) la estructura se deforma de modo característico, al perder su rigidez inicial frente a la deformación (en ciertos sentidos privilegiados). Figura: Modelo a escala para ser probado a presión 57 A partir de la superación del límite de proporcionalidad, la estructura se encuentra en un régimen llamado inelástico, y cuando alcanza la fluencia se denomina en régimen plástico, aunque no se detecte nada especial ya que este régimen solo afecta a zonas muy limitadas de la estructura, permaneciendo la gran parte de ella en régimen elástico o inelástico. En general, alcanzar el estado plástico es un caso raro ya que, al disminuir sustancialmente el modulo E, el pandeo por inestabilidad, en cualquiera de sus tipos, aparece irremisiblemente. Limitándonos al caso concreto de un cilindro reforzado por cuadernas regularmente espaciadas, sometido a una presión exterior creciente, se tiene que los puntos mas cargados por tensiones son los situados bien en el centro de las claras, parte exterior del forro, o bien los puntos de contacto cuaderna forro, por la parte interior del forro. Las tensiones máximas, pueden ser en el sentido transversal (circunferencial) o longitudinal (en sentido del eje del cilindro, producidas por los momentos que induce la existencia de las cuadernas), en función de la clara y el espesor de forro. Supongamos que los puntos más cargados son los correspondientes a los extremos de las claras, en su punto de contacto con las cuadernas, por el interior del forro, que es el caso más corriente, con tensiones máximas en el sentido longitudinal. Cuando la presión se eleva lo suficiente para que se alcance el límite de proporcionalidad del material en los puntos descritos, resultará que existirá una línea circunferencial, formando un anillo transversal que habrá superado este límite, en el extremo de cada clara. Por ser solo una fibra superficial y aislada esto no tiene trascendencia y no tiene carácter de peligro inminente, pensando en las tensiones exclusivamente. Si se sigue aumentando la presión, estas fibras se irán propagando (hacia el interior del forro y hacia las zonas contiguas) y se irán formando unas rótulas de carácter inelástico. Al mismo tiempo se puede ir formando otra rotula en el centro de la clara, empezando por la fibra mas externa, si las tensiones máximas están próximas alas que existían en el extremo de clara, ya que es la segunda zona mas cargada, aunque las tensiones máximas sean en sentido transversal y, llegado un momento, se puede producir un mecanismo con tres rótulas alineadas en cada clara. El material se deformará con facilidad y sobrevendrá la ruina de la estructura que, en este caso teórico, comenzará transformando el cilindro en una especie de acordeón, al aproximarse las cuadernas entre si. Lo mismo sucedería si es el punto central de las claras el primero que entra en plastificación, seguido por la plastificación de los puntos de extremo de clara. Obsérvese que esta explicación simplificada del fenómeno, no se ha tenido en cuenta que el estado de tensiones es bidireccional. Se han supuesto unas rotulas, pero que no son de la misma constitución. Las rótulas que se generan en el extremo de las claras tienen el eje de giro en sentido transversal al cilindro (están producidas por tensiones longitudinales que superan el limite de fluencia), sin embargo las tensiones transversales en estas rotulas son mas reducidas. Las rótulas que se generan en el centro de las claras son también con eje transversal, pero con las tensiones transversales también muy altas. Ya se verá como se determinan estas tensiones en los capítulos que siguen. En experimentos con modelos nunca se obtiene, o es muy difícil, la forma de acordeón perfecta y simétrica respecto al eje del cilindro, (ya que la respuesta mecánica del material no es homogénea, los espesores pueden ser ligeramente diferentes, con unas tensiones internas o deformaciones iniciales etc.), sino que pueden formarse arrugas en una zona de una sola clara, la mas débil. En la Figura nº 16 pude observarse este tipo de pandeo que solo ha afectado a una clara y además, solo parcialmente. De haberse continuado la prueba, probablemente hubiesen aparecido más ondas entre claras (en forma de fuelle). En pruebas con modelos en tanque de presión, al ser limitada la reserva de fluido presurizado, las deformaciones que se obtienen, una vez que se alcanza el estado de mecanismo, son de pequeña amplitud (ya que la bomba que alimenta el tanque de prueba es de un caudal limitado y la presión aplicada, externa, se reduce mucho al encogerse el 58 cilindro) pero en los casos reales, es decir, en el mar, la deformación progresa muy rápidamente hasta el aplastamiento total en sentido longitudinal, en el caso mas ideal. En la práctica, termina aplastándose según otros modos de fallo. Hay que entender que, en las figuras que presentan de modos de fallo, obtenidos en tanques de pruebas, sobre modelos, estas solo representan el comienzo o iniciación de los modos de colapso, suspendiéndose en este punto la prueba. De haber efectuado estas mismas pruebas en condiciones naturales, es decir sumergiendo los modelos en el mar, en resultado hubiera sido, en todos los casos, un colapso total y violento de estas estructuras, por lo cual la determinación del modo de fallo estaría expuesta a incertidumbres. Se ha supuesto, deliberadamente, que durante todas las fases del fenómeno de la plastificación y posterior colapso no han interferido otras posibles formas de fallo con el fin de describir tal como ocurriría de forma teóricamente pura. Se ha supuesto que la estructura posee suficiente rigidez o resistencia a los restantes modos de fallo, permitiendo a la estructura penetrar en el campo plástico sin contemplar ningún tipo de interferencias, lo que no siempre ocurre. Por lo general, cuando se ha formado un gran número de rótulas plásticas o rótulas alienadas, es muy difícil evitar que aparezcan, simultáneamente, otros tipos de inestabilidad local o general. En la Foto anexa se presenta el fallo por plastificación de una estructura provista de un anillo de forma tronco-cónica, en la parte superior. En este tipo de recintos cónicos, la plastificación entre cuadernas, en acordeón, es más propensa a ocurrir ya que las tensiones longitudinales son muy fuertes por motivo de los momentos flectores provocados por el cambio de radio. Las secciones de radio más pequeño se embuten en las de radio mayor. Obsérvese que en la parte cilíndrica, parte inferior de la figura, ha aparecido una deformación, muy bien marcada, de plastificación. Esto es típico en las zonas de unión de un cilindro de pared gruesa y otro de pared delgada (o entre un cilindro y un mamparo conexo) por las grandes tensiones de discontinuidad que aparecen. En estructuras cilíndricas de acero, una vez alcanzado el límite de proporcionalidad, si está cercano al de fluencia, las zonas inelásticas se propagan muy rápidamente, entrando en plastificación y posteriormente en ruina con moderados incrementos de la presión. El 59 proceso de propagación de la plastificación es muy complejo, habiéndose estudiado de forma teórica por numerosos autores entre los que destaca P. G. Hodge, ref nº 4 que ha obtenido aproximaciones muy buenas en las predicciones. Son soluciones, no obstante, muy elaboradas y de carácter muy teórico, necesitándose cierto tiempo para que puedan ser de aplicación práctica o de uso común. En la inmensa mayoría de los casos la presión de colapso se encuentra comprendida entre la que produce Ia primera fluencia (las primeras fibras que entran en fluencia) y un 110 % de esta. Por consiguiente una vez conocida la presión que produce la iniciación de la plastificación se está muy cerca de la verdadera presión de colapso. En este aspecto, hay algunos aceros de alto límite elástico, que muestran una separación apreciable entre el límite de proporcionalidad y el límite de fluencia. En este intervalo, hay puntos que, sin llegar a ser el limite de fluencia nominal, disponen de tan bajo modulo de rigidez, E, que, en la práctica, es como si la fueran. La rigidez de la estructura se descompone y se reduce tanto que jamás se alcanza el límite de fluencia nominal. La estructura colapsa por inestabilidad. Hay que señalar que la tensión de fluencia del forro, al estar sometido a un estado biaxial de tensiones, no corresponde exactamente con la tensión de fluencia nominal del material en ensayo uniaxial. En el caso de cilindros, en los que la tensión transversal media, es aproximadamente el doble que la axial o longitudinal media, la tensión de fluencia admisible, de cálculo es, aproximadamente, 1,16 veces la nominal, unidireccional, (Criterio de Von Mises-Hencky). 60 En el proyecto de cilindros reforzados se pretende que el modo de fallo preferente sea por plastificación. Ello será índice de se ha apurado el material al máximo, ya que no se puede concebir que el cilindro aguante unas tensiones superiores a las de fluencia, a compresión casi pura, sin deformarse o entrar en ruina. No obstante, la pericia del diseñador será obtener un reparto de tensiones que sea lo mas ajustado posible (minimizando las componentes de la tensión derivadas de la flexión) dentro de la geometría del modelo considerado, para retrasar su entrada en régimen inelástico, es decir evitando que haya puntos singulares o zonas muy cargadas y propensos a plastificar anticipadamente. Se ha creído, hace tiempo, que el mejor diseño de forro era aquél en que se igualaban las tensiones en los puntos mas significativos de la clara, (centro y extremo de clara), pero no es este el criterio exclusivo que define la rotura. La existencia de otros modos de fallo (elástico o inelástico) que dependen relativamente poco de las tensiones de clara, ha conducido a que esta igualdad no sea la que optimiza la resistencia global. No obstante, se considera que las tensiones máximas en los puntos significativos no deben diferir mas del 25% entre si, para aprovechar el material al máximo, todo ello compaginado con los modos de fallo que se prevean como mas críticos. 61 Una forma de reducir o anular la creación de un mecanismo por situación de una rótula en el centro de las claras es mediante el montaje de longitudinales entre cuaderna y cuaderna con poca separación entre si, soldados al forro. Con ello se aumenta la inercia longitudinal de la plancha entre cuadernas y permite retrasar el colapso, en este modo, de la estructura. Evidentemente esto supone mayor peso de la misma y una mayor complejidad constructiva, por lo que su uso solo está justificado para presiones de 100 bar (1000 m de cota) o mayores, a partir de las que esta forma de reforzado puede aventajar a la tradicional, a base únicamente de cuadernas. 7.4.4. Fallo por inestabilidad del forro entre cuadernas Este tipo de fallo se identifica por la creación de lóbulos o abultamientos, alternados hacia adentro y hacia afuera (estos menos pronunciados), repartidos circunferencialmente, en la franja de forro comprendida entre dos cuadernas. Estos lóbulos forman una especie de ondas en sentido circunferencial. Las cuadernas no se deforman apenas, limitándose a tomar una torsión alternada, en fase y a demanda del forro. Cuando este fenómeno sucede en varias claras contiguas, se produce con un desfase de media longitud de onda de los abultamientos de una clara y la contigua. En el sentido longitudinal las generatrices del cilindro forman una sinusoide. Por consiguiente, las deformaciones son anti-simétricas respecto a las cuadernas situándose sobre ellas el punto de inflexión de la ondulación longitudinal y permaneciendo estas circulares. Este tipo de pandeo puede ocurrir en el régimen elástico o inelástico del material. Ver Fig. nº 17. Su existencia teórica se conoce desde hace bastante tiempo, principios del siglo XX, pero su visualización ha sido difícil habiendo sido conseguido este modo de pandeo en ensayos efectuados en 1951, sobre modelos. Este tipo de fallo puede ocurrir en cascos con forros de poco espesor y cuadernas relativamente fuertes y separadas. Este fallo era el mas susceptible de ocurrir en los submarinos anteriores a la 2ª Guerra Mundial, que tenían pequeños espesores de forro, (de 14 a 18 mm). En los actuales, que precisan unos mayores espesores, al ser las cotas operativas más grandes, no es un modo crítico tan usual, ( y los proyectistas se esmeran en que no lo sea). En las optimizaciones que se efectúan en la actualidad, con el objeto de reducir del peso, se obtienen claras relativamente reducidas, lo que favorece la estabilidad, aunque el uso de aceros de alto limite elástico se contrapone al efecto anterior, ya que al poderse subir el nivel de tensiones la inestabilidad, de cualquier tipo, se favorece. Además, se tiende a aumentar las claras, respecto a las óptimas, para simplificar la construcción, al reducirse el número necesario de cuadernas a construir, su influencia en la disposición general, etc. Por consiguiente sigue siendo muy necesaria la estimación de la presión crítica de este modo de fallo. Existen también motivos de carácter no estructural que obligan a una separación determinada de las cuadernas, como puede ser la disposición de las baterías entre cuaderna y cuaderna, de unas medidas concretas, o la necesidad de que las brazolas de las escotillas no interrumpan o interfieran demasiado con las cuadernas. En general, aumentar la clara de las cuadernas es beneficioso para la disposición general, el montaje de los pasos de casco, etc, al haber mas espacio disponible entre unas y otras. El número de ondas en sentido circunferencial es de 8 a 10, como mínimo, siendo la longitud de las semi-ondas muy similar a la clara entre cuadernas. El colapso sobreviene como consecuencia de los grandes esfuerzos y momentos de flexión que aparecen en las planchas del forro provocados por esta deformación lobular asimétrica, lográndose instantáneamente, a continuación, el aplastamiento de la estructura completa. Como ya se ha dicho, en las pruebas con modelos, en tanques de presión, puede paralizarse la deformación en sus comienzos y así poder analizar su forma y características. Puede verse afectado este modo por la plastificación de zonas locales del 62 forro por lo que es muy difícil disociarlo del colapso por plastificación, en estructuras de espesores medianos. El estudio teórico de este modo de inestabilidad se efectuará en el Apartado de cilindros. Este modo de inestabilidad se estudia como el de un cilindro sin refuerzos de una longitud igual a una clara entre cuadernas, apoyado o empotrado en los extremos (que equivale a la sujeción que aportan las cuadernas). En realidad las cuadernas no ejercen ninguna restricción al giro de la plancha de forro unida a ellas, por ser su rigidez a la torsión muy pequeña, (son perfiles abiertos), por lo que la condición de bordes mas apropiada es la de simple apoyo. Puesto que las cuadernas ceden un poco en dirección radial por efecto de la fuerza que les transmite el forro, sometido a presión exterior, la condición real de apoyo en bordes es la de simplemente apoyados sobre base elástica. Esta rigidez de la base dependerá de la robustez de las cuadernas y por consiguiente, a título puramente teórico, se debería obtener una ley de pandeo que fuese también función de las rigideces de las cuadernas adyacentes, pero este efecto se desprecia. Con el fin de simplificar, solamente se suele calcular la presión crítica de este modo de inestabilidad en función de las 63 características geométricas generales de la clara y de las propiedades mecánicas (módulo de Young, E) del material utilizado. En general, no se determinan presiones críticas sino tensiones críticas que hay que comparar con las admisibles por el material que forma el forro o con las realmente deba soportar, bajo una cierta presión aplicada a la parte exterior del cilindro. Las tensiones críticas (matemáticas) obtenidas se obtienen, siempre, suponiendo que el material es infinitamente elástico y el módulo de elasticidad, E, constante. Para transformar estas tensiones criticas elásticas en tensiones en régimen inelástico hay que efectuar unas correcciones en las que se incluye el modulo de elasticidad tangente, etc. En la Foto anexa se puede observar un cilindro que ha sufrido un pandeo entre cuadernas, que ha afectado a dos claras contiguas. Foto obtenida de Ref. nº 65. 64