Difusión Enfoque atomístico

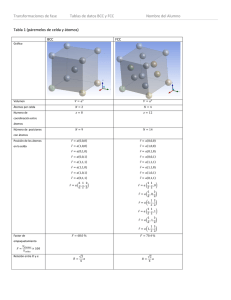
Difusión
Enfoque atomístico
Estructura cristalina
Ma. Eugenia Noguez Amaya
Objetivos
• Repaso estructura de solidos cristalinos (Redes de
Bravais)
• Tipos de estructuras
• Representaciones gráficas
• Parámetro de red y radio atómico
• Sitios intersticiales
• Repaso Vectores
• Difusión en solidos como mecanismo de las
transformaciones de fase
• Saltos dentro de una red cristalina durante la difusión
Redes de Bravais
• La estructura de los solidos cristalinos (no amorfos) puede
clasificarse de acuerdo al acomodo de sus átomos.
• Existen 14 posibles acomodos para los átomos de un solido
cristalino, las representaciones geométricas mas pequeñas de
la estructura cristalina es lo que se conoce como las redes de
Bravais, estudiadas por francés Aguste Bravais en 1850.
• Las estructuras mas comunes en las aleaciones metálicas son
• HCP (Hexagonal Closed Packed) hexagonal compacta
• BCC (Body Centered Cubic) cubica centrada en el cuerpo
• FCC (Face Centered Cubic) cubica centrada en las caras
• Una celda unitaria es el arreglo mas pequeño que representa
la geometría de un solido y al transponerlo muchas veces se
obtiene la estructura cristalina
Primitivo (Simple)
Triclínico
Monoclínico
Ortorrómbico
Tetragonal
Centrado en un par de
caras
Centrado en las caras
Centrado en el cuerpo
Primitivo (Simple)
Romboédrico (Trigonal)
Hexagonal
Cubico
Centrado en un par de
caras
Centrado en las caras
Centrado en el cuerpo
Representaciones Gráficas
• Existen diversas formas de representar gráficamente un sistema cristalino a fin de visualizar mejor
la estructura real o analizar la geometría
Parámetros importantes de
una celda
• 𝑎, 𝑏, 𝑐 representan el
tamaño de la celda se
conoce como parámetros
de red y están el orden de
Å o 0.1 nm. (Para sistemas
cúbicos solo se necesita
especificar 𝑎 , para
hexagonal 𝑎 y 𝑐, etc.)
• 𝑅 representa el radio
atómico está el orden de Å
o 0.1 nm. (Generalmente
existen ecuaciones para
relacionar los parámetros
de red 𝑎, 𝑏, 𝑐 con el radio.)
a
R
Ejemplos de relación entre a y R para
sistemas cúbicos
• FCC
• 𝑅=
• BCC
2
𝑎
4
• 𝑅=
3
𝑎
4
Tipos de sitios intersticiales
• Existen dos tipos de sitios
intersticiales en cualquiera de
las 14 redes de Bravais
• Octaédricos
• Tetraédricos
• Los datos relevantes para los
sitios intersticiales son
• Posición dentro de la celda
unitaria
• Numero de sitios por celda
unitaria
• Distancia de un sitio intersticial
al otro
• Numero de coordinación (sitios
intersticiales vecinos)
• Tamaño del átomo que puede
estar en el sitio intersticial
Sitios intersticiales en la celda
BCC
• Sitios octaédricos
• Sitios tetraédricos
Sitios intersticiales en la celda
FCC
• Sitios octaédricos
• Sitios tetraédricos
Relación r/R
• Para saber si un átomo cabe en un intersticio se utiliza la
relacion 𝑟/𝑅 donde 𝑟 es el tamaño máximo que cabría en un
sitio intersticial de una celda con átomos de radio 𝑅
• Para cada tipo de celda hay dos relaciones 𝑟/𝑅 una para los
sitios tetraédricos y otra para los octaédricos
Puntos dentro de una celda
• Algunos puntos de una son de particular interés, por ejemplo
los puntos donde se encuentran los átomos
• Los puntos dentro de una celda se representan con vectores
𝑟 = 𝑎 0,0,0
1 1 1
𝑟=𝑎 , ,
2 2 2
𝑟 = 𝑎 1,1,1
Repaso Vectores
• 𝑎 = 𝑎1 , 𝑎2 , 𝑎3 , 𝑏 = 𝑏1 , 𝑏2 , 𝑏3 , 𝑟1 = 1,2,3 y 𝑟2 = 4,5,6 vectores
• 𝑐 y 𝑑 escalares
• Multiplicación por escalar
• (𝑐)𝑎 = 𝑐 𝑎1 , 𝑎2 , 𝑎3 = 𝑐𝑎1 , 𝑐𝑎2 , 𝑐𝑎3
• (𝑑)𝑟1 = 3 1,2,3 = 3,6,9
• Resta vectores
• 𝑎 − 𝑏 = 𝑎1 − 𝑏1 , 𝑎2 − 𝑏2 , 𝑎3 − 𝑏3
• 𝑟1 − 𝑟2 = 1 − 4,2 − 5,3 − 6 = −3, −3, −3
• Producto punto
• 𝑎 ∙ 𝑏 = 𝑎1 𝑏1 , 𝑎2 𝑏2 , 𝑎3 𝑏3
• 𝑟1 ∙ 𝑟2 =
1 4 , (2)(5), (3)(6) = 4,10,18
• Magnitud de un vector
•
𝑎 = 𝑎∙𝑎 =
•
𝑟1 =
1
2
+ 2
𝑎1
2
2
+ 𝑎2
+ 3
2
2
+ 𝑎3
= 14
2
Difusión
• La difusión es el fenómeno donde átomos o moléculas son transportados desde una
zona con concentración alta a otra con menor concentración.
• Existen dos formas de estudiar la difusión
• Modelos atomísticos: se basan en analizar los arreglos atómicos en los solidos y
saltos aleatorios dentro de una estructura cristalina
• Modelos fenomenológicos: se basan en analizar la composición en un sistema
suponiendo que es un medio continuo a través de las leyes de Fick
Tipos de difusión
• Existen básicamente dos
tipos de difusión en el estado
solido
• Difusión sustitucional: en
este caso se considera que un
átomo se desplaza dentro de
la estructura cristalina desde
algún punto en la red hacia
una vacancia
• Difusión intersticial: los
átomos que difunden se
desplazan entre los sitios
intersticiales dentro de la
estructura cristalina
Determinacion de la distancia de
salto α
• Suponiendo una solución intersticial en una celda FCC donde el soluto solo puede
estar en los sitios octaédricos
1 1 1
• ¿Un átomo que se encuentra en el sitio 𝑟1 = 𝑎 2 , 2 , 2 y brinca hasta el otro sitio
1
𝑟2 = 𝑎 2 , 1,1 cual es la distancia de salto 𝛼?
• Por supuesto esto es para un salto especifico generalmente se debería tomar o el
promedio o la moda entre todos los posibles saltos 𝛼 en la red
• Para obtener 𝛼 se utiliza la fórmula de distancia entre dos puntos 𝛼 = 𝑑 = ∆𝑟 =
∆𝑟 ∙ ∆𝑟
• Desarrollando los términos se tendría como
𝛼 = ∆𝑟 = 𝑎
𝑟2 − 𝑟1 ∙ 𝑟2 − 𝑟1
1 1
• Para nuestro caso ∆𝑟 = 𝑟2 − 𝑟1 = 𝑎 0, 2 , 2
• ∆𝑟 ∙ ∆𝑟 =
• 𝛼=𝑎
1
2
02
=
+
𝑎
2
1 2
2
+
1 2
2
2
1
=4=2
Resumen
• Estructuras de solidos (redes de Bravais); estructuras comunes HCP,
BCC y FCC; representaciones gráficas
• Parámetros de red (𝑎, 𝑏, 𝑐 ) y su relación con el radio atómico (𝑅 )
• Sitios intersticiales tetraédricos y octaédricos; análisis en las celdas
BCC y FCC
• Tamaño del sitio intersticial; relación (𝑟/𝑅)
• Puntos en una celda 𝑟
• Repaso vectores; multiplicación por escalar, resta de vectores,
producto punto y magnitud.
• Difusión; descripción del fenómeno y tipos de difusión en solidos
(intersticial y sustitucional)
• Determinación de la distancia de salto 𝛼 a partir de la formula de
distancia entre dos puntos.
Actividad 2
• En una hoja de Calculo Excel
• Buscar el valor del radio atómico de átomo de Fe, Cr y C
(Incluir unidades en nm)
• A partir del valor de radio atómico de Fe obtener el parámetro
de red 𝑎 para las fases Austenita (FCC) y Ferrita (BCC). (Incluir
unidades en nm)
• Determinar el radio máximo para los intersticios de Austenita
𝑟
y Ferrita a partir de la relación ; comparar los resultados con
𝑅
el radio del átomo de C. (Incluir unidades en nm) ¿Dónde se
encontraran los átomos de C en intersticios tetraédricos o
octaédricos?
Actividad 2
• ¿El cromo en las aleaciones que tipo de difusión tendría
sustitucional o intersticial?, ¿Porqué?
• Se tiene una aleación intersticial de C en Austenita (FCC),
obtener la distancia de salto (𝛼) promedio, moda, máxima y
mínima. (ayudarse de la hoja de cálculo proporcionada con
todas las combinaciones posibles de salto)
Objetivos Actividad 2
•
•
•
•
•
•
•
Formato fracciones
Producto punto
Promedio
Moda
Valor Máximo
Valor mínimo
Raíz cuadrada