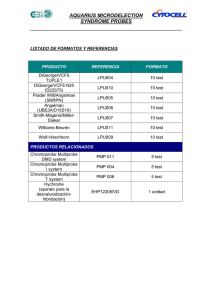
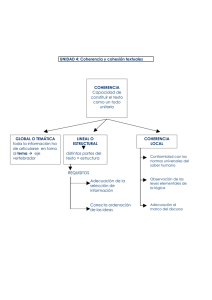
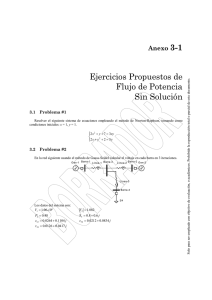
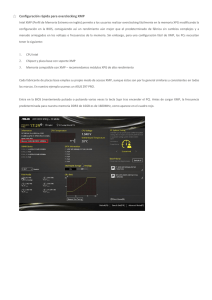
∫∫ ∫∫ ∫ ∫
Anuncio

ÓPTICA ESTADÍSTICA GRUPO PILOTO CURSO 2006/2007 Solucionario Ejercicio No.6 De acuerdo con el enunciado del ejercicio en el plano de la fuente Z=0 tenemos una intensidad mutua asociada a dicha fuente definida: r Γ s, s,0 = I 0circ 2R ( ) (1) En las condiciones de aproximación para una fuente de Carter-Wolf emitiendo en el límite incoherente en condiciones de cuasi-monocromaticidad, el grado de coherencia espacial se obtiene aplicando el Teorema de Van Cittert-Zernike: l Γ ( P1 , P2 ;0 ) = β ∫∫ x y Γ s, s;0 exp − ik xs 12 + ys 12 dxs dys −∞ z12 z12 ( +∞ ) (2) l es una constante compleja, y x , y , z son coordenadas reducidas. donde: β 12 12 12 Por conveniencia escribiremos la ec.(2) como: l Γ ( P1 , P2 ;0 ) = β ∫∫ +∞ −∞ ( ) Γ s, s;0 exp −2π i ( xsu12 + ys v12 ) dxs dys Donde hemos introducido las frecuencias espaciales: u12 = (3) x12 y , v12 = 12 . λ z12 λ z12 Debido a la geometría de la fuente debemos de trabajar en coordenadas polares. Para ello consideramos el siguiente cambio de variable: xs = r cosθ ys = rsenθ Sustituyendo la ec.(1) en la ec.(3) y operando teniendo en cuenta el Jacobiano: l Γ ( ρ ,φ ;0 ) = I 0 β R ∫∫ 0 2π 0 exp ( −2π i ρ r cosθ cos φ ) exp ( −2π i ρ r senθ senφ ) rdrdθ (4) Donde: u12 = ρ cos φ v12 = ρ senφ Nótese que: ρ = u122 + v122 = 1 r v y x122 + y122 = 12 ; φ = arctan 12 = arctan 12 . λ z12 λ z 12 u12 x12 Operando en la ec.(4): l Γ ( ρ ,φ ;0 ) = I 0 β R ∫∫ 0 2π 0 exp −2π i ρ r cos (θ − φ ) rdrdθ (5) La integral de la ec.(5) se puede realizar utilizando la representación integral de las funciones de Bessel. En general: i−n Jn ( x) = 2π ∫ 2π 0 exp ( − ix cosθ ) exp ( inθ ) dθ (6) Donde por n denotamos el orden de la función de Bessel. Por tanto, en la ec.(5): l Γ ( ρ ;0 ) = 2π I 0 β ∫ R 0 J 0 ( 2πρ r ) rdr (7) La ec.(7) expresa la transformada de Bessel-Fourier de la intensidad mutua asociada a la fuente circular. Haremos uso de la siguiente propiedad de la función de Bessel de orden cero: ∫ x 0 J 0 ( x ') x ' dx ' = xJ1 ( x ) (8) Donde J1 es la función de Bessel de orden uno. Sustituyendo en la ec.(7): l Γ ( ρ ;0 ) = π R 2 I 0 β La función 2 J1 ( 2πρ R ) ( 2πρ R ) (9) 2 J1 ( 2πρ R ) se denomina función Besinc, puesto que es una representación ( 2πρ R ) análoga a la sinc pero en coordenadas polares. Por tanto sus ceros tienen valores no enteros. El módulo cuadrado de la función Besinc se denomina “función de Airy”1. En particular, anotaremos como dato el primer cero de la función Besinc: 1,22π = 3,833; 2 ρ R = 1,22; ρ = 1,22 0,61 . También es importante el dato del = 2R R radio del disco central correspondiente al máximo de energía. 1 Véase: M. Born, E. Wolf, Principles of Optics, Capítulo 8, sección 8.5. Editorial Cambridge University Press, 7a edición, 1999. De acuerdo con el resultado de la ec.(9) el grado de coherencia espacial de la fuente circular, viene expresado según el módulo de la función Besinc normalizada a su valor máximo en el origen: 2π Rr12 2 J1 λ z12 2 J1 ( 2πρ R ) = γ ( ρ ;0 ) = 2π Rr12 ( 2πρ R ) λ z12 (10) Las figuras 1, 2 y 3 representan respectivamente el comportamiento numérico de la ec.(9) para los parámetros que intervienen en la propagación de la intensidad mutua. γ ( r12 ;0) r12 (mm) Figura 1.- Comportamiento del grado de coherencia espacial de un fuente circular. Datos numéricos: λ=600 nm., distancia de propagación: z12 = 1m., radio de la fuente: R=65 mm. Obsérvese que el primer cero de la función se encuentra para: r12 = 5,5 µm. El radio de coherencia se puede entonces estimar de acuerdo con este valor (siguiendo el criterio del experimento de Verdet). γ ( r12 ;0) r12 (mm) Figura 2.- En este caso se ha tomado como dato del radio de la fuente: R=6,5 cm. Se aprecia que el grado de coherencia espacial disminuye de forma importante con respecto al comportamiento obtenido en la figura 1. γ ( r12 ;0) z12 (m) Figura 3.- Evolución del grado de coherencia espacial con la distancia de propagación. Datos numéricos análogos a la figura 1, con r12 fijo: r12 = 0,002 mm. Se observa que la coherencia espacial aumenta con la propagación de la correlación obteniéndose un valor casi estable para una propagación del orden de 2 m.