Problema. Considere el método de Runge

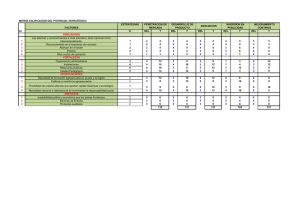
Problema. Considere el método de Runge-Kutta de cinco etapas dado por el tablero
0
1/2
1/2
1
1
0
1/2
0 1/2
0
0
1
1/6 1/3 1/3 1/6
1/6 1/3 1/3 1/12 1/12
1. Diseñe una función de Matlab que implemente el método anterior y cuyos argumentos de entrada sean la correspondiente función f un, el instante inicial t0 , el
instante final tf , el valor inicial y0 y el tamaño del paso h.
2. Obtenga una tabla con los errores relativos, en t = 1, cometidos al integrar el sistema
diferencial
½ 0
x1 (0) = 1
x1 = x1
,
,
0
x2 (0) = 1
x2 = −x2
mediante el método Runge-Kutta anterior para h = 0.1, 0.01, 0.001, 0.0001. A la
vista de la tabla, determine experimentalmente el orden del método anterior.
3. Considere ahora el sistema diferencial
½ 0
y1 = 1 + y12 y2 − 4y1
,
y20 = 3y1 − y12 y2
y1 (0) = 1.5
.
y2 (0) = 0
Usando el método anterior, determine en formato largo la expresión
y1 (5) + y20 (5)
para h = 0.001. Asimismo, en el intervalo [0, 10], esboce la gráfica de y1 que se
obtiene para dicho valor de h.
(1)
function [T,Y]=rungekutta(fun,t0,tf,y0,h)
T=(t0:h:tf)’;
n=length(T);
Y=zeros(n,length(y0));
y0=y0(:);Y(1,:)=y0’;
for k=1:n-1
k1=feval(fun,T(k),Y(k,:))’;
k2=feval(fun,T(k)+0.5*h,Y(k,:)+0.5*h*k1)’;
k3=feval(fun,T(k)+0.5*h,Y(k,:)+0.5*h*k2)’;
k4=feval(fun,T(k)+h,Y(k,:)+h*k3)’;
k5=feval(fun,T(k)+h,Y(k,:)+(h/6)*(k1+2*k2+2*k3+k4))’;
Y(k+1,:)=Y(k,:)+(h/12)*(2*k1+4*k2+4*k3+k4+k5);
end
(2)
function apartado2(p)
h=1;
for k=1:p
h=h/10;
[T,Y]=rungekutta(@fun,0,1,[1,1],h);
n=length(T);
error_rel=norm(Y(n,:)-[exp(1),exp(-1)])/norm([exp(1),exp(-1)]);
fprintf(’h=10^(-%1.0f) Error_Rel=%16.15f\n’,k,error_rel)
pause(0.1)
end
function dydt=fun(t,y)
dydt=[y(1);-y(2)];
Ejecutamos el fichero:
>> apartado2(5)
h=10^(-1) Error_Rel=0.000006743891679
h=10^(-2) Error_Rel=0.000000006924364
h=10^(-3) Error_Rel=0.000000000006942
h=10^(-4) Error_Rel=0.000000000000003
h=10^(-5) Error_Rel=0.000000000000002
El método es de orden tres pues se ganan tres posiciones en cada iteración.
(3)
function apartado3
[T,Y]=rungekutta(@fun,0,5,[1.5,0],0.001);
n=length(T);
valor=Y(n,1)+3*Y(n,1)-Y(n,1)^2*Y(n,2);
fprintf(’y1(5)+y2(5)=%16.15f\n’,valor)
pause
[T,Y]=rungekutta(@fun,0,10,[1.5,0],0.001);
plot(T,Y(:,1)),shg
function dydt=fun(t,y)
dydt=[1+y(1)^2*y(2)-4*y(1)
3*y(1)-y(1)^2*y(2)];
Ejecutamos el fichero:
>> apartado3
y1(5)+y2(5)=0.933714376481227
2
4
3.5
3
2.5
2
1.5
1
0.5
0
0
2
4
6
3
8
10