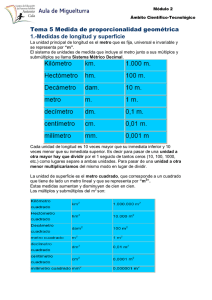
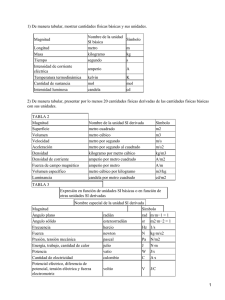
nom-008-scfi-1993 sistema general de unidades de medida general

NOM-008-SCFI-1993
SISTEMA GENERAL DE UNIDADES DE MEDIDA
GENERAL SYSTEM OF UNITS
NOM-008-SCFI-1993
PREFACIO
En la elaboración de esta norma participaron las siguientes instituciones, organismos y
empresas:
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE LA INDUSTRIA DE
LA CONSTRUCCIÓN
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE ENVASE Y
EMBALAJE
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN METROLÓGICA
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE CALDERAS Y
RECIPIENTES A PRESIÓN
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE SISTEMAS DE
CALIDAD
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN PARA LA VIVIENDA
DE INTERÉS SOCIAL CON ELEMENTOS DE MADERA
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE LA INDUSTRIA DE
ACEITES Y GRASAS COMESTIBLES Y SIMILARES
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE LA INDUSTRIA
ELECTRÓNICA Y DE COMUNICACIONES ELÉCTRICAS
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE LA INDUSTRIA
SIDERÚRGICA
- COMITÉ CONSULTIVO NACIONAL DE NORMALIZACIÓN DE PRODUCTOS DE LA
PESCA
- SECRETARÍA DE AGRICULTURA Y RECURSOS HIDRÁULICAS. DIRECCIÓN
GENERAL DE POLÍTICA AGRÍCOLA
- SECRETARÍA DE DESARROLLO URBANO Y ECOLOGÍA. DIRECCIÓN GENERAL
DE NORMAS E INSUMOS DE VIVIENDA
- CENTRO DE INVESTIGACIÓN Y ESTUDIOS AVANZADOS DEL IPN
- INSTITUTO NACIONAL DE INVESTIGACIONES NUCLEARES
- INSTITUTO MEXICANO DEL ALUMINIO, A.C.
- CÁMARA NACIONAL DE LA INDUSTRIA DE TRANSFORMACIÓN
- FERTILIZANTES MEXICANOS, S.A. DIRECCIÓN DE OPERACIÓN INDUSTRIAL
- FORD MOTOR COMPANY
- COMPAÑÍA MANTEQUERA MONTERREY, S.A. DE C.V.
- INSTITUTO MEXICANO DEL SEGURO SOCIAL
NORMA OFICIAL MEXICANA: NOM-008-SCFI-1993
SISTEMA GENERAL DE UNIDADES DE MEDIDA
(Esta Norma cancela la NOM-Z-1-1979)
INTRODUCCIÓN
Esta norma tiene como propósito, establecer un lenguaje común que responda a las exigencias
actuales de las actividades científicas, tecnológicas, educativas, industriales y comerciales, al
alcance de todos los sectores del país.
La elaboración de este documento se basó en las resoluciones y acuerdos que sobre el Sistema
Internacional de Unidades (SI) se han tenido en la Conferencia General de Pesas y Medidas
(CGPM), hasta su 19a. Convención realizada en 1991.
El "SI" es el primer sistema de unidades de medición compatible, esencialmente completo y
armonizado internacionalmente, está fundamentado en 7 unidades de base, cuya
materialización y reproducción objetiva de los patrones correspondientes, facilita a todas las
naciones que la adopten, la estructuración de sus sistemas metrológicos a los más altos niveles
de exactitud. Además, al compararlo con otros sistemas de unidades, se manifiestan otras
ventajas entre las que se encuentran la facilidad de su aprendizaje y la simplificación en la
formación de las unidades derivadas.
1
OBJETIVO Y CAMPO DE APLICACIÓN
Esta Norma establece las definiciones, símbolos y reglas de escritura de las unidades del
Sistema Internacional de Unidades (SI) y otras unidades fuera de este Sistema que acepte la
CGPM, que en conjunto, constituyen el Sistema General de Unidades de Medida, utilizado en
los diferentes campos de la ciencia, la tecnología, la industria, la educación y el comercio.
2
REFERENCIAS
Para la correcta aplicación de esta norma se debe consultar la siguiente Norma
NMX-Z-55
3
Metrología-Vocabulario de términos fundamentales generales
DEFINICIONES FUNDAMENTALES
Para los efectos de esta norma, se aplican las definiciones contenidas en la norma referida en
el inciso 2 y las siguientes:
3.1
Sistema Internacional de Unidades (SI)
Sistema coherente de unidades adoptado por la Conferencia General de Pesas y Medidas
(CGPM).
Este sistema está compuesto por:
- unidades SI base;
- unidades SI suplementarias;
- unidades SI derivadas;
NOM-008-SCFI-1993
2/74
3.2
Unidades SI base
Unidades de medida de las magnitudes de base del Sistema Internacional de Unidades.
3.3
Magnitud
Atributo de un fenómeno, cuerpo o substancia que es susceptible a ser distinguido
cualitativamente y determinado cuantitativamente.
3.4
Sistema coherente de unidades (de medida)
Sistema de unidades compuesto por un conjunto de unidades de base y de unidades derivadas
compatibles.
3.5
Magnitudes de base
Son magnitudes que dentro de un "sistema de magnitudes" se aceptan por convención, como
independientes unas de otras.
3.6
Unidades suplementarias
Son unidades que se definen geométricamente y pueden tener el carácter de unidad de base o
de unidad derivada.
3.7
Unidades derivadas
Son unidades que se forman combinando entre sí las unidades de base, o bien, combinando
las unidades de base, con las unidades suplementarias según expresiones algebraicas que
relacionan las magnitudes correspondientes de acuerdo a leyes simples de la física.
4
TABLAS DE UNIDADES
4.1
Unidades SI base
Actualmente las unidades base del SI son 7, correspondiendo a las siguientes magnitudes;
longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura termodinámica,
intensidad luminosa y cantidad de sustancia. Los nombres de las unidades son
respectivamente: metro, kilogramo, segundo, ampere, kelvin, candela y mol. Las magnitudes,
unidades, símbolos y definiciones se describen en la Tabla 1.
4.2
Unidades SI suplementarias
Estas unidades son el radián y el esterradián; las magnitudes, unidades, símbolos y
definiciones se describen en la Tabla 2.
4.3
Unidades SI derivadas
4.3.1 Estas unidades se obtienen a partir de las unidades de base y de las unidades
suplementarias, se expresan utilizando los símbolos matemáticos de multiplicación y división.
Se pueden distinguir tres clases de unidades la primera, la forman aquellas unidades SI
derivadas expresadas a partir de unidades de base de las cuales se indican algunos ejemplos
en la Tabla 3; la segunda la forman las unidades SI derivadas que reciben un nombre especial
y símbolo particular, la relación completa se cita en la Tabla 4; la tercera la forman las
unidades SI derivadas expresadas con nombres especiales, algunos ejemplos de ellas se
indican en la Tabla 5.
NOM-008-SCFI-1993
3/74
4.3.2 Existe gran cantidad de unidades derivadas que se emplean en las áreas científicas,
para una mayor facilidad de consulta, se han agrupado en 10 tablas, correspondiendo a un
número equivalente de campos de las mas importantes la física, de acuerdo a la relación
siguiente:
Tabla 6
Principales magnitudes y unidades de espacio y tiempo.
Tabla 7
Principales magnitudes y unidades de fenómenos periódicos y conexos.
Tabla 8
Principales magnitudes y unidades de mecánica.
Tabla 9
Principales magnitudes y unidades de calor.
Tabla 10
Principales magnitudes y unidades de electricidad y magnetismo.
Tabla 11
Principales magnitudes y unidades de luz y radiaciones electromagnéticas.
Tabla 12
Principales magnitudes y unidades de acústica.
Tabla 13
Principales magnitudes y unidades de físico-química y física molecular.
Tabla 14
Principales magnitudes y unidades de física atómica y física nuclear.
Tabla 15
Principales magnitudes y unidades de reacciones nucleares y radiaciones
ionizantes.
NOM-008-SCFI-1993
4/74
Tabla 1. Nombres, símbolos y definiciones de las unidades SI base
Magnitud
Unidad
Símbolo
masa
kilogramo
kg
tiempo
segundo
s
corriente eléctrica
ampere
A
temperatura
termodinámica
kelvin
K
cantidad de
substancia
mol
mol
intensidad
luminosa
candela
cd
longitud
metro
m
Definición
Es la longitud de la trayectoria por la luz
en el vacío durante un intervalo de tiempo
de 1/299 792 458 de segundo [17a. CGPM
(1983) Resolución 1]
Es la masa igual a la del prototipo
internacional del kilogramo [1a. y 3a.
CGPM (1889 y 1901)]
Es la duración de 9 192 631 770 períodos
de la radiación correspondiente a la
transición entre los dos niveles hiperfinos
del estado fundamental del átomo de cesio
133 [13a. CGPM (1987), Resolución 1]
Es la intensidad de una corriente constante
que mantenida en dos conductores
paralelos rectilíneos de longitud infinita,
cuya área de sección circular es
despreciable, colocados a un metro de
distancia entre sí, en el vacío, producirá
entre estos conductores una fuerza igual a
2x10-7 newton por metro de longitud [9a.
CGPM, (1948), Resolución 2]
Es la fracción 1/273,16 de la temperatura
termodinámica del punto triple del agua
[13a. CGPM (1967) Resolución 4]
Es la cantidad de substancia que contiene
tantas entidades elementales como existen
átomos en 0,012 kg de carbono 12 [14a.
CGPM (1971), Resolución 3]
Es la intensidad luminosa en una dirección
dada de una fuente que emite una
radiación monocromática de frecuencia
540x1012 hertz y cuya intensidad
energética en esa dirección es 1/683 watt
por esterradián [16a. CGPM (1979),
Resolución 6]
NOM-008-SCFI-1993
5/74
Tabla 2. Nombres de las magnitudes, símbolos y definiciones de las unidades SI
suplementarias
Magnitud
Unidad
Símbolo
ángulo sólido
esterradián
sr
ángulo plano
radián
rad
Definición
Es el ángulo plano comprendido entre dos
radios de un círculo y que interceptan
sobre la circunferencia de este círculo un
arco de longitud igual a la del radio (ISOR-31/1)
Es el ángulo sólido que tiene su vértice en
el centro de una esfera, y, que intercepta
sobre la superficie de esta esfera una área
igual a la de un cuadrado que tiene por
lado el radio de la esfera (ISO-R-31/1)
Tabla 3
Ejemplo de unidades SI derivadas sin nombre especial
Magnitud
superficie
volumen
velocidad
aceleración
número de ondas
masa volúmica, densidad
volumen específico
densidad de corriente
intensidad de campo eléctrico
concentración
(de
cantidad
substancia)
luminancia
Unidades SI
Nombre
metro cuadrado
metro cúbico
metro por segundo
metro por segundo cuadrado
metro a la menos uno
kilogramo por metro cúbico
metro cúbico por kilogramo
ampere por metro cuadrado
ampere por metro
de mol por metro cúbico
candela por metro cuadrado
Símbolo
m2
m3
m/s
m/s2
m-1
kg/m3
m3/kg
A/m2
A/m
mol/m3
cd/m2
NOM-008-SCFI-1993
6/74
Tabla 4
Unidades SI derivadas que tienen nombre y símbolo especial
Magnitud
frecuencia
fuerza
presión,
tensión
mecánica
trabajo,
energía,
cantidad de calor
potencia,
flujo
energético
carga
eléctrica,
cantidad
de
electricidad
diferencia
de
potencial,
tensión
eléctrica,
potencial
eléctrico,
fuerza
electromotriz
capacidad eléctrica
resistencia eléctrica
conductancia
eléctrica
flujo magnético1
inducción magnética2
inductancia
flujo luminoso
luminosidad3
actividad nuclear
dosis absorbida
temperatura Celsius
equivalente de dosis
Nombre de la
Expresión en
unidad SI
Símbolo unidades SI
derivada
de base
Expresión en
otras
unidades SI
Hz
N
Pa
s-1
m.kg.s-2
m-1.kg.s-2
joule
J
m2.kg.s-2
N.m
watt
W
m2.kg.s-3
J/s
coulomb
C
s.A
volt
V
m2.kg.s-3.A-1
W/A
farad
ohm
siemens
F
Ω
S
m-2.kg-1.s4.A2
m2.kg.s-3.A-2
m-2.kg-1.s3.A2
C/V
V/A
A/V
Wb
T
H
lm
lx
Bq
Gy
°C
Sv
m2.kg.s-2.A-1
kg.s-2.A-1
m2.kg.s-2.A-2
cd. sr
m-2.cd.sr
s-1
m2.s-2
V.s
Wb/m2
Wb/A
hertz
newton
pascal
weber
tesla
henry
lumen
lux
becquerel
gray
grado Celsius
sievert
m2.s-2
1 también llamado flujo de inducción magnética.
2 también llamada densidad de flujo magnético.
3 también llamada iluminancia.
N/m2
lm/m2
J/kg
K
J/kg
NOM-008-SCFI-1993
7/74
Tabla 5
Ejemplos de unidades SI derivadas expresadas por medio de nombres especiales
Magnitud
viscosidad dinámica
momento de una fuerza
tensión superficial
densidad de flujo de calor,
irradiancia
capacidad calorífica, entropía
capacidad calorífica específica,
entropía específica
energía específica
conductividad térmica
densidad energética
fuerza del campo eléctrico
densidad de carga eléctrica
densidad de flujo eléctrico
permitividad
permeabilidad
energía molar
entropía molar, capacidad calorífica
molar
exposición (rayos x y γ)
rapidez de dosis absorbida
Nombre
Unidad SI
Símbolo
Expresión en unidades SI de base
Pa.s
N.m
N/m
m-1 kgs-1
m2.kg.s-2
kg.s-2
W/m2
J/K
kg.s-3
m2.kg.-2.K-1
joule por kilogramo kelvin
joule por kilogramo
watt por metro kelvin
joule por metro cúbico
volt por metro
coulomb por metro cúbico
coulomb por metro cuadrado
farad por metro
henry por metro
joule por mol
J/(kg.K)
J/kg
W/(m.K)
J/m3
V/m
C/m3
C/m2
F/m
H/m
J/mol
m2s-2.K-1
m2.s-2
m.kg.s-3.K-1
m-1.kg.s-2
m.kg.s-3.A-1
m-3.s.A
m-2.s.A
m-3.kg-1.s4.A2
m.kg.s-2.A-2
m2.kg.s-2.mol-1
joule por mol kelvin
coulomb por kilogramo
gray por segundo
J/(mol.K)
C/kg
Gy/s
m2.kg.s-2.K-1.mol-1
kg-1.s.A
m2.s-3
pascal segundo
newton metro
newton por metro
watt por metro cuadrado
joule por kelvin
NOM-008-SCFI-1993
8/74
Tabla 6 Principales magnitudes y unidades de espacio y tiempo
Magnitud
Símbolo de la
magnitud
ángulo plano
α, β, γ, υ, ϕ, etc.
ángulo sólido
Ω
longitud
ancho
altura
espesor
radio
diámetro
longitud de trayectoria
área o superficie
volumen
tiempo, intervalo de
tiempo, duración
velocidad angular
l, (L)
b
h
d, δ
r
d, D
s
A, (S)
V
t
aceleración
α
ω
Definición de la magnitud
El ángulo comprendido entre dos semirectas
que parten del mismo punto, se define como
la relación de la longitud del arco
intersectado por estas rectas sobre el círculo
(con centro en aquel punto), a la del radio
del círculo
El ángulo sólido de un cono se define como
la relación del área cortada sobre una
superficie esférica (con su centro en el
vértice del cono) al cuadrado de la longitud
del radio de la esfera.
dϕ
ω= ----dt
dω
α= ----dt
Unidad SI
Símbolo de la unidad
SI
radián
(véase Tabla 2)
rad
esterradián
(véase Tabla 2)
sr
metro
(véase Tabla 1)
m
metro cuadrado
metro cúbico
segundo
(véase Tabla 1)
radián por segundo
m2
m3
s
rad/s
radián por segundo rad/s2
al cuadrado
NOM-008-SCFI-1993
9/74
Tabla 6 (continuación)
velocidad
u, v, w, c
ds
v= ----dt
metro por segundo
aceleración
a
dv
a= -----dt
metro por segundo al m/s2
cuadrado
aceleración de caída g
libre, aceleración debida
a la gravedad
Nota: la aceleración normal de caída libre
es:
gn = 9,806 65 m/s2
(Conferencia General de Pesas y
Medidas 1901)
m/s
NOM-008-SCFI-1993
10/74
Tabla 7 Magnitudes y unidades de fenómenos periódicos y conexos
Magnitud
Símbolo de la
magnitud
período,
tiempo T
periódico
constante de tiempo de τ, (T)
un magnitud que varía
exponencialmente
frecuencia
f, υ
Definición de la magnitud
Unidad SI
Tiempo de un ciclo
segundo
s
Tiempo después del cual la magnitud podría
alcanzar su límite si se mantiene su
velocidad inicial de variación
segundo
s
1
f= ------
hertz
Símbolo de la unidad
SI
Hz
t
frecuencia de rotación
n
frecuencia
angular ω
frecuencia
circular,
pulsatancia
longitud de onda
λ
número de onda
σ
número de onda circular k
Número de revoluciones dividido por el segundo recíproco
tiempo
ω = 2πf
radián por segundo
segundo recíproco
s-1
Distancia, en la dirección de propagación de
una onda periódica, entre dos puntos en
donde, en un instante dado, la diferencia de
fase es 2π
m
1
σ= ---λ
k = 2πσ
metro
metro recíproco
rad/s
s-1
m-1
NOM-008-SCFI-1993
11/74
Tabla 7 (Continuación)
diferencia de nivel de LF
amplitud, diferencia de
nivel de campo
diferencia de nivel de LP
potencia
coeficiente
amortiguamiento
de δ
LF = 1n (F1/F2)
donde F1 y F2 representan dos amplitudes
de la misma clase
neper*
decibel*
1
LP -------- 1n (P1/P2)
neper*
2
decibel*
donde P1 y P2 representan dos potencias
Si una magnitud es una función del tiempo segundo recíproco
y está determinada por:
Np*
dB*
Np*
dB*
s-1
F(t) = Ae-δtsen[ω(t-to)]
decremento logarítmico
coeficiente
atenuación
Λ
de α
entonces δ es el coeficiente de
amortiguamiento
producto
del
coeficiente
de neper*
amortiguamiento y el período
Si una magnitud es una función de la metro recíproco
distancia x y está dada por:
F(x) = Ae-αxcos[β(x-xo)]
coeficiente de fase
coeficiente
propagación
β
de γ
entonces α es el coeficiente de atenuación y
β es el coeficiente de fase
γ=α+jβ
* éstas no son unidades del SI pero se mantienen para usarse con unidades del SI
1 No es la diferencia de nivel de amplitud cuando 1n )F1/F2) = 1
1 dB es la diferencia de nivel de amplitud cuando 20 1g (F1/F2) = 1
Np*
m-1
NOM-008-SCFI-1993
12/74
Tabla 8 Magnitudes y unidades de mecánica
Magnitud
masa
Símbolo de la
magnitud
Definición de la magnitud
m
Unidad SI
kilogramo
kg
(véase Tabla 1)
kilogramo por metro kg/m3
cúbico
densidad
(masa
volúmica)
densidad relativa
ρ
masa dividida por el volumen
d
volumen específico
v
densidad lineal
densidad superficial
ρl
ρA,(ρS)
Relación de la densidad de una substancia
con respecto a la densidad de una substancia
de referencia bajo condiciones que deben
ser especificadas para ambas substancias
Volumen dividido por la masa
metro cúbico por
kilogramo
Masa dividida por la longitud
kilogramo por metro
Masa dividida por el área
kilogramo por metro
cuadrado
Producto de la masa y la velocidad
kilogramo metro por
segundo
El momento de momentum de una partícula kilogramo
metro
con respecto a un punto es igual al producto cuadrado
por
vectorial del radio vector dirigido del punto segundo
hacia la partícula, y el momentum de la
partida
El momento (dinámico) de inercia de un kilogramo
metro
cuerpo con respecto a un eje, se define cuadrado
como la suma (la integral) de los productos
de sus masas elementales, por los cuadrados
de las distancias de dichas masas al eje
cantidad de movimiento,
momentum
momento de momentum,
momentum angular
momento de inercia
(momento dinámico de
inercia)
P
L
I, J
Símbolo de la unidad
SI
m3/kg
kg/m
kg/m2
kg.m/s
kg.m2/s
kg.m2
NOM-008-SCFI-1993
13/74
Tabla 8 (continuación)
fuerza
peso
constante gravitacional
F
G, (P, W)
g, (f)
La fuerza resultante aplicada sobre un newton
cuerpo es igual a la razón de cambio del
momentum del cuerpo
N
El peso de un cuerpo en un determinado
sistema de referencia se define como la
fuerza que, aplicada al cuerpo, le
proporciona una aceleración igual a la
aceleración local de caída libre en ese
sistema de referencia
La fuerza gravitacional entre dos partículas newton
metro N.m2/kg2
m1m2
cuadrado
por
es F= ---------kilogramo cuadrado
r2
donde r es la distancia entre las partículas,
m1 y m2 son sus masas y la constante
gravitacional es:
momento de una fuerza
M
momento
torsional,
momento de un par
presión
T
P
esfuerzo normal
esfuerzo al corte
σ
τ
G= (6,672 0 ± 0,004 1) 10-11 N.m2/kg2
El momento de una fuerza referido a un newton metro
punto es igual al producto vectorial del
radio vector, dirigido desde dicho punto a
cualquier otro punto situado sobre la línea
de acción de la fuerza, por la fuerza
La fuerza dividida por el área
pascal
N.m
Pa
NOM-008-SCFI-1993
14/74
Tabla 8 (continuación)
módulo de elasticidad
E
E = σ/ε
módulo
de
rigidez,
módulo de corte
G
G = τ/γ
módulo de comprensión
compresibilidad
K
K
K = -o/ϑ
1 dv
pascal recíproco
Pa-1
K = ----------v dp
El momento segundo axial de área de una metro a la cuarta m4
área plana, referido a un eje en el mismo potencia
plano, es la suma (integral) de los productos
de sus elementos de área y los cuadrados de
sus distancias medidas desde el eje
momento
área
segundo
de
momento segundo polar
de área
módulo de sección
Ia, (I)
Ip
Z, w
pascal
El momento segundo polar de área de una
área plana con respecto a un punto
localizado en el mismo plano, se define
como la integral de los productos de sus
elementos de área y los cuadrados de las
distancias del punto a dichos elementos de
área
El módulo de sección de un área plana o metro cúbico
sección con respecto a un eje situado en el
mismo plano, se define como el momento
segundo axial de área dividido por la
distancia desde el eje hasta el punto más
lejano de la superficie plana
Pa
m3
NOM-008-SCFI-1993
15/74
Tabla 8 (continuación)
η, (µ)
viscosidad dinámica
viscosidad cinemática
ν
γ, σ
tensión superficial
trabajo
W, (A)
energía
E, (W)
energía potencial
Ep, V, Φ
energía cinética
potencia
gasto masa, flujo masa
Ek, K, T
P
qm
gasto volumen,
volumen
flujo
qv
τxz = η dvx/dz
donde τxz es el esfuerzo cortante de un
fluido en movimiento con un gradiente
dvx
de velocidad -------- perpendicular al
dz
plano de corte
ν = η/ρ
donde:
ρ es la densidad
Se define como la fuerza perpendicular a un
elemento de línea en una superficie,
dividida por la longitud de dicho elemento
de línea
Fuerza multiplicada por el desplazamiento
en la dirección de la fuerza
pascal segundo
Pa . s
metro cuadrado por m2/s
segundo
newton por metro
N/m
joule
J
Razón de transferencia de energía
watt
Cociente de la masa que atraviesa una kilogramo
superficie por el tiempo
segundo
Razón a la cual el volumen cruza una metro cúbico
superficie
segundo
W
por kg/s
por m3/s
NOM-008-SCFI-1993
16/74
Tabla 9 Magnitudes y unidades de calor
Magnitud
temperatura
termodinámica
temperatura Celsius
Símbolo de la
magnitud
T, θ
t, θ
Definición de la magnitud
La temperatura termodinámica se define
según los principios de la termodinámica
t = T - To
donde t y T son temperaturas Celsius y
termodinámicas de un mismo sistema, y
donde To es fijada convencionalmente
como To = 273,15 K
1 d
αl = - --
coeficiente de dilatación
lineal
αl
coeficiente de dilatación
cúbica
αv, γ
1 dV
αv = --- ---V dT
coeficiente de presión
relativa
αp
coeficiente de presión
compresibilidad
β
κ
calor, cantidad de calor
Q
1 dp
αp = --- ---p dT
β = dp/dT
1 dV
κ = ----- ----v dp
Unidad SI
Símbolo de la unidad
SI
kelvin
(véase Tabla 1)
grado Celsius
K
°C
kelvin recíproco
K-1
pascal por kelvin
pascal recíproco
Pa/K
Pa-1
joule
J
l dT
NOM-008-SCFI-1993
17/74
Tabla 9 (Continuación)
flujo térmico
densidad
de
flujo
térmico
conductividad térmica
Φ
q, ϕ
λ, (k)
coeficiente
de
transferencia de calor
aislamiento
térmico,
coeficiente
de
aislamiento térmico
resistencia térmica
h, k, K, α
difusividad térmica
a, (α, κ)
capacidad térmica
M
R
C
Flujo de calor a través de una superficie
Flujo térmico dividido por el área
considerada
Densidad de flujo térmico dividido por el
gradiente de temperatura
Densidad de flujo térmico dividido por la
diferencia de temperaturas
Diferencia de temperaturas dividida por la
densidad de flujo térmico
watt
watt
por
metro
cuadrado
watt
por
metro
kelvin
watt
por
metro
cuadrado kelvin
metro
cuadrado
kelvin por watt
W
W/m2
W/(m.K)
W/(m2.K)
(m2.K)/W
Diferencia de temperatura dividida por el kelvin por watt
K/W
flujo térmico
λ
metro cuadrado por m2/s
a = ---segundo
ρcp
donde
λ es la conductividad térmica
ρ es la densidad;
cp es la capacidad térmica específica a
presión constante
Cuando la temperatura de un sistema se joule por kelvin
incremente una cantidad diferencial dT,
como resultado de la adición de una
pequeña cantidad de calor dQ, la magnidQ
tud
---- es la capacidad térmica
dT
Tabla 9 (Continuación)
J/K
NOM-008-SCFI-1993
18/74
capacidad
específica
térmica
c
capacidad
específica
constante
a
térmica
presión
cp
capacidad
específica
constante
a
térmica
volumen
cv
capacidad
térmica
específica a saturación
entropía
Capacidad térmica dividida por la masa
joule por kilogramo J/(kg.K)
kelvin
csat
S
Cuando una cantidad pequeña de calor dQ joule por kelvin
es recibida por un sistema cuya temperatura
termodinámica es T, la
J/K
dQ
entropía del sistema se incrementa en ___
T
energía interna
U, (E)
considerando
que
ningún
cambio
irreversible tiene lugar en el sistema
Entropía dividida por la masa
joule por kilogramo J/(kg.K)
kelvin
joule
J
entalpía
H, (I)
H = U+pV
energía libre Helmholtz,
función Helmholtz
A, F
A = U-TS
entropía específica
energía libre
función Gibbs
Gibbs,
s
G
G = U+pV-TS; G = H-TS
NOM-008-SCFI-1993
19/74
Tabla 9 (Continuación)
energía
específica
interna
entalpía específica
u, (e)
Energía interna dividida por la masa
h, (i)
Entalpía dividida por la masa
energía libre específica
Helmholtz,
función
específica Helmholtz
a, f
energía libre específica
Gibbs,
función
específica Gibbs
función Massieu
función Planck
g
Energía libre Gibbs dividida por la masa
J
Y
J = -A/T
Y = -G/T
joule por kilogramo
J/kg
joule por kelvin
joule por kelvin
J/K
J/K
Energía libre Helmholtz dividida por la
masa
Tabla 10 Magnitudes y unidades de electricidad y magnetismo
NOM-008-SCFI-1993
20/74
Magnitud
corriente eléctrica
carga eléctrica, cantidad
de electricidad
densidad
de
carga
densidad volumétrica de
carga
densidad superficial de
carga
intensidad de campo
eléctrico
I
Q
ρ, (η)
σ
E, (K)
V, ϕ
potencial eléctrico
diferencia de potencial,
tensión eléctrica
fuerza electromotriz
densidad
de
eléctrico,
desplazamiento
Símbolo de la
magnitud
flujo
U, (V)
E
D
Definición de la magnitud
Unidad SI
Símbolo de la unidad
SI
ampere (ver tabla 1) A
Integral de la corriente eléctrica con coulomb
C
respecto al tiempo
Carga dividida por el volumen
coulomb por metro C/m3
cúbico
coulomb por metro C/m2
cuadrado
Fuerza ejercida por un campo eléctrico volt por metro
V/m
sobre una carga eléctrica puntual, dividida
por el valor de la carga
Para campos electrostáticos, una magnitud volt
V
escalar, en el cual el gradiente tiene signo
contrario y es igual al valor de la intensidad
de campo eléctrico
Carga dividida por el área superficial
La tensión entre dos puntos 1 y 2 es la
integral de línea desde el punto 1 hasta el
punto 2 de la intensidad de campo eléctrico
2
ϕ1-ϕ2 = ∫ Esds
1
La fuerza electromotriz de una fuente es la
energía suministrada por la fuente dividida
por la carga eléctrica que pasa a través de la
fuente
La densidad de flujo eléctrico es una coulomb por metro C/m2
magnitud vectorial, cuya divergencia es cuadrado
igual a la densidad de la carga
NOM-008-SCFI-1993
21/74
Tabla 10 (Continuación)
flujo eléctrico, (flujo de
desplazamiento)
ψ
capacitancia
C
permitividad
ε
permitividad del vacío,
constante eléctrica
εο
permitividad relativa
susceptibilidad eléctrica
polarización eléctrica
momento
eléctrico
dipolo
densidad de corriente
εr
χ, χe
P
P, (Pe)
J, (S)
El flujo eléctrico a través de un elemento de coulomb
superficie es el producto escalar del
elemento de superficie y la densidad de
flujo eléctrico
Carga dividida por la diferencia de farad
potencial eléctrico
Densidad de flujo eléctrico dividido por la farad por metro
intensidad de campo eléctrico
C
F
F/m
1
εο = ---- c2
µο
= (8,854 187 818 ± 0, 000 000 071) x 1012 F/m
εr = ε/ εο
χ = εr -1
P = D-εο E
coulomb por metro C/m2
cuadrado
El momento dipolo eléctrico es una coulomb metro
C.m
magnitud vectorial, cuyo producto vectorial
con la intensidad de campo eléctrico es
igual al "par"
Es una magnitud vectorial cuya integral ampere por metro A/m2
evaluada para una superficie especificada, cuadrado
es igual a la corriente total que circula a
través de dicha superficie
NOM-008-SCFI-1993
22/74
Tabla 10 (Continuación)
densidad
corriente
intensidad
magnético
lineal
de
de
campo
diferencia de potencial
magnético
fuerza magnetomotriz
A, (α)
H
Um
F, Fm
corriente totalizada
densidad
de
flujo
magnético,
inducción
magnética
θ
B
flujo magnético
Φ
potencial
magnético
vectorial
A
Corriente dividida por el espesor de la placa ampere por metro
conductora
La intensidad de campo magnético es una ampere por metro
magnitud vectorial axial cuya rotacional es
igual a la densidad de corriente, incluyendo
a la corriente de desplazamiento
La diferencia de potencial magnético entre ampere
el punto y el punto 2 es igual a la integral de
línea, desde el punto 1 hasta punto 2 de la
intensidad de campo eléctrico
A/m
A/m
A
F = ∫ Hsds
Corriente eléctrica neta de conducción neta
a través de un bucle cerrado
La densidad de flujo magnético es una tesla
magnitud vectorial axial tal que la fuerza
ejercida sobre un elemento de corriente, es
igual al producto vectorial de este elemento
y la densidad de flujo magnético
El flujo magnético que atraviesa un weber
elemento de superficie es igual al producto
escalar del elemento de superficie y la
densidad de flujo magnético
El potencial vectorial magnético es una weber por metro
magnitud vectorial, cuya rotacional es igual
a la densidad de flujo magnético
T
Wb
Wb/m
NOM-008-SCFI-1993
23/74
Tabla 10 (Continuación)
autoinductancia
L
inductancia mutua
coeficiente
acoplamiento
M, L12
de
k, (κ)
En una espiral conductora, es igual al flujo henry
magnético de la espiral, causada por la
corriente que circula a través de ella,
dividido por esa corriente
H
En dos espirales conductoras es el flujo
magnético a través de una espiral producido
por la corriente circulante en la otra espiral
dividido por el valor de esta corriente
coeficiente de dispersión
σ
σ= 1-k2
permeabilidad
µ
Densidad de flujo magnético, dividida por henry por metro
la intensidad de campo magnético
permeabilidad del vacío,
constante magnética
permeabilidad relativa
susceptibilidad
magnética
momento
electromagnético
(momento magnético)
µο
µο = 4π x 10-7 H/m
µο = 12,566 370 614 4 x 10-7 H/m
µr = µ/µο
κ = µr-1
µr
κ, (χm)
m
El momento electromagnético es una ampere
magnitud vectorial, cuyo producto vectorial cuadrado
con la densidad del flujo magnético es igual
al par
H/m
metro A·m2
NOM-008-SCFI-1993
24/74
Tabla 10 (Continuación)
magnetización
Hi , M
polarización magnética
densidad de energía
electromagnética
vector de Poynting
Bi, J
w
velocidad
de
propagación de ondas
electromagnéticas en el
vacío
c
resistencia
(a
corriente continua)
la
R
conductancia
(a
corriente continua)
resistividad
la
G
S
ρ
B
Hi= ------ H
µο
Bi = B-µοH
Energía del campo electromagnético
dividida por el volumen
El vector de Poynting es igual al producto
vectorial de la intensidad de campo
eléctrico y la intensidad de campo
magnético
1
c = -------√εο µο
ampere por metro
tesla
joule por
cúbico
watt
por
cuadrado
T
metro J/m3
metro W/m2
metro por segundo
c = (2,997 924 58 ± 0,000 000 012x108
m/s
La diferencia de potencial eléctrico dividida ohm
por la corriente, cuando no existe fuerza
electromotriz en el conductor
G = 1/R
siemens
Intensidad de campo eléctrico dividido por ohm metro
la densidad de corriente cuando no existe
fuerza electromotriz dentro del conductor
A/m
m/s
Ω
S
Ω.m
NOM-008-SCFI-1993
25/74
Tabla 10 (Continuación)
conductividad
γ, σ
reluctancia
R, Rm
permeancia
Λ, (P)
γ = 1/ρ; el símbolo κ se utiliza en siemens por metro
S/m
electroquímica
Diferencia de potencial magnético dividido henry a la menos uno H-1
por el flujo magnético
1
henry
H
Λ = ------Rm
Cuando u = um cos ω t
e i = im cos (ωt-ϕ)
diferencia
de
fase
desplazamiento de fase
ϕ
impedancia,
(impedancia compleja)
Z
módulo de impedancia
(impedancia)
IZI
reactancia
X
Parte imaginaria de la impedancia
1
X = Lω ----Cω
resistencia
R
factor de calidad
Q
Parte real de la impedancia
(véase resistencia a la corriente continua)
Q = IXI/R
ϕ es el desplazamiento de fase
La representación compleja de la diferencia ohm
de potencial, dividida por la representación
compleja de la corriente
Tabla 10 (Continuación)
Ω
NOM-008-SCFI-1993
26/74
admitancia (admitancia
compleja)
Y
módulo de admitancia
(admitancia)
IYI
1
Y = ------Z
siemens
susceptancia
B
Parte imaginaria de la admitancia
conductancia
G
potencia
P
Parte real de la admitancia (véase
conductancia a la corriente continua)
Producto de la corriente y la diferencia de watt
potencial
S
W
cuando:
u = um cos ωt= √2u cos ωt
y
i = im cos (ωt - ϕ) = √2 I cos (ωt - ϕ)
se tiene que:
iu es la potencia instantánea (símbolo p)
IU cos ϕ es la potencia activa (símbolo p)
IU es la potencia aparente [símbolo S, (Ps)]
IU sen ϕ es la potencia reactiva [símbolo Q,
(pq)]
el nombre "factor de potencia" (símbolo γ)
se usa para la relación P/S
NOM-008-SCFI-1993
27/74
Tabla 11 Magnitudes y unidades de luz y radiaciones electromagnéticas
Magnitud
frecuencia
frecuencia circular
longitud de onda
número de onda
número de onda circular
velocidad
de
propagación de ondas
electromagnéticas en el
vacío
energía radiante
densidad de energía
radiante
concentración espectral
de densidad de energía
radiante (en términos de
longitud de onda)
potencia radiante, flujo
de energía radiante
Símbolo de la
magnitud
f, ν
ω
λ
σ
k
c, co
Q, W
(U, Qe)
w, (u)
wλ
P, Φ, (Φe)
Definición de la magnitud
Número de ciclos dividido por el tiempo
ω= 2π
La distancia en la dirección de propagación
de una onda periódica entre dos puntos
sucesivos cuya fase es la misma
σ = 1/λ
Unidad SI
hertz
segundo recíproco
metro
Hz
s-1
m
metro recíproco
m-1
k = 2πσ
c = 2,997 924 58 + 0,000 000 012)x108 m/s metro por segundo
Energía emitida, transferida o recibida como
radiación
Energía radiante en un elemento de
volumen, dividido por ese elemento
La densidad de energía radiante en un
intervalo infinitesimal de longitud de onda,
dividido por el alcance de ese intervalo
Símbolo de la unidad
SI
joule
m/s
J
joule por metro J/m3
cúbico
joule por metro a la J/m4
cuarta potencia
Potencia emitida, transferida o recibida watt
como radiación
W
NOM-008-SCFI-1993
28/74
Tabla 11 (continuación)
densidad
de
flujo
radiante, razón de flujo
de energía radiante
ϕ, ψ
intensidad radiante
I, (Ie)
radiancia
L, (Le)
excitancia radiante
M, (Me)
irradiancia
E, (Ee)
constante de
Boltzmann
Stefan
σ
En un punto en el espacio, el flujo de
energía radiante incidente sobre una esfera
pequeña, dividida por el área de la sección
transversal de esa esfera
Para una fuente en una dirección
determinada, la potencia radiante que fluye
hacia el exterior de la fuente o un elemento
de la fuente, en un elemento de ángulo
sólido que contenga a la dirección dada,
dividida por dicho elemento de ángulo
sólido
En un punto de una superficie y en una
dirección determinada, la intensidad
radiante de un elemento de esa superficie,
dividida por el área de las proyección
ortogonal de dicho elemento sobre un plano
perpendicular a la dirección dada
En un punto de una superficie, el flujo de
energía radiante que fluye hacia el exterior
de un elemento de esa superficie, dividido
por el área de dicho elemento
En un punto de una superficie, el flujo de
energía radiante que incide sobre un
elemento de esa superficie, dividida por el
área de dicho elemento
La constante σ en la expresión para la
excitancia radiante de un radiador total
(cuerpo negro), a la temperatura
termodinámica T
M = σ·T4
por
watt
cuadrado
metro W/m2
watt por esterradián
W/sr
watt por esterradián W/sr·m2
metro cuadrado
watt
por
cuadrado
metro W/m2
watt
por
cuadrado
metro W/m2
watt
por
metro W/(m2·k4)
cuadrado kelvin a la
cuarta potencia
NOM-008-SCFI-1993
29/74
Tabla 11 (continuación)
primera constante
radiación
de
c1
segunda constante
radiación
de
c2
ε
emisividad
emisividad
espectral,
emisividad
a
una
longitud
de
onda
específica
emisividad
direccional
espectral
intensidad luminosa
ε(λ)
ε(λ, θ, ϕ)
(I, Iv)
flujo luminoso
Φ, (Φv)
cantidad de luz
Q, (Qv)
Las constantes c1 y c2 en la expresión para watt metro cuadrado W·m2
la concentración espectral de la excitancia
radiante de un radiador total a la
temperatura termodinámica T:
λ-5
metro kelvin
m·K
Mλ = c1f(λ,T) = c1 ---------------exp (c2/λT)-1
c1 = 2πhc2
c2 = hc/k
Relación de la excitancia radiante de un
radiador térmico a la de un radiador total
(cuerpo negro) a la misma temperatura
Relación de la concentración espectral de la
excitancia radiante de un radiador térmico a
la de un radiador total (cuerpo negro) a la
misma temperatura
Relación de la concentración espectral de
radiancia en una dirección dada θ, de un
radiador térmico a la de un radiador total
(cuerpo negro) a la misma temperatura
candela
(véase Tabla 1)
El flujo luminoso dΦ de una fuente de lumen
intensidad luminosa I dentro de un elemento
de ángulo sólido Ω es
dΦ = IdΩ
Integral en función del tiempo del flujo lumen segundo
luminoso
Tabla 11 (continuación)
cd
lm
lm·s
NOM-008-SCFI-1993
30/74
luminancia
L, (Lv)
excitancia luminosa
M, (Mv)
luminosidad
(iluminancia)
E, (Ev)
exposición de luz
H
eficacia luminosa
k
eficacia
espectral
luminosa,
eficacia
luminosa a una longitud
de onda específica
eficacia
luminosa
espectral máxima
La luminancia un punto de una superficie y
en una dirección dada, se define como la
intensidad luminosa de un elemento de esa
superficie, dividida por el área de la
proyección ortogonal de este elemento
sobre un plano perpendicular a la dirección
considerada
La excitancia luminosa en un punto de una
superficie, se define como el flujo luminoso
que fluye hacia el exterior de un elemento
de la superficie, dividido por el área de ese
elemento
La luminosidad en un punto de una
superficie, se define como el flujo luminoso
que incide sobre un elemento de la
superficie dividido por el área de ese
elemento
candela por metro cd/m2
cuadrado
lumen por
cuadrado
lux
lux segundo
H = ∫ E dt (integral en el tiempo de la
iluminancia)
Φv
lumen por watt
K = ---------Φe
K(λ)
Φvλ
K(λ) = --------Φ eλ
Km
El valor máximo de K(λ)
Tabla 11 (continuación)
metro lm/m2
lx
lx·s
lm/W
NOM-008-SCFI-1993
31/74
ν
eficiencia luminosa
eficiencia
luminosa
espectral,
eficiencia
luminosa a una longitud
de onda específica
valores
triestímulos
espectrales CIE
coordenadas
cromaticidad
de
ν(λ)
x (λ), y (λ),
z (λ)
x, y, z
K
ν = --------Km
K(λ)
ν(λ) = -----Km
Valores triestímulos de las componentes
espectrales de un estímulo equienergético
en el sistema tricomático X, Y, Z. Estas
funciones son aplicables a campos
observación entre 1° y 4°. En este sistema y
(λ)def ν(λ)
Para luz cuya concentración espectral de
flujo radiante sea
∫ (λ) x (λ)dλ
Χ=----------------------------------------------∫ (λ)x(λ)dλ+∫ (λ)y(λ)dλ+∫ (λ)z(λ)dλ
Análogamente se definen y z. Para fuentes
de luz
(λ)= Φeλ(λ)/Φeλ(λο)
(flujo radiante espectral relativo)
Para colores de objetos se calcula por uno
de los tres productos
Φeλ(λ)
(λ)= -------------Φeλ(λο)
ρ(λ)
τ(λ)
β(λ)
Tabla 11 (continuación)
NOM-008-SCFI-1993
32/74
absorbancia espectral
a (λ)
reflectancia espectral
transmitancia espectral
ρ(λ)
τ(λ)
coeficiente de radiancia
espectral
β(λ)
coeficiente
de
atenuación
lineal,
coeficiente de extinción
lineal
µ
coeficiente de absorción
lineal
coeficiente de absorción
molar
a
κ
Relación de las concentraciones espectrales
de los flujos radiantes absorbido e incidente
Relación de las concentraciones espectrales
de los flujos radiantes reflejado e incidente
Relación de las concentraciones espectrales
de los flujos radiantes transmitido e
incidente
El factor de radiancia espectral en un punto
de un superficie y en una dirección dada, es
el cociente entre las concentraciones
espectrales de radiancia de un cuerpo no
radiante por sí mismo y de un difusor
perfecto, igualmente irradiados
La disminución relativa en la concentración metro recíproco
m-1
espectral del flujo luminoso o radiante de un
haz colimado de radiación electromagnética
al cruzar un medio laminar de espesor
infinitesimal, dividida por la longitud
atravesada
La parte del coeficiente de atenuación
debida a la absorción
κ =a/c
metro cuadrado por m2/mol
mol
donde c es la concentración de cantidad de
substancia
NOM-008-SCFI-1993
33/74
Tabla 11 (continuación)
índice de refracción
n
El índice de refracción de un medio no
absorbente
para
una
radiación
electromagnética de frecuencia dada, es la
relación entre la velocidad de las ondas (o
de la radiación) en el vacío a la velocidad de
fase en el medio
NOM-008-SCFI-1993
34/74
Tabla 12 Magnitudes y unidades de acústica
Magnitud
período,
tiempo
periódico
frecuencia
intervalo de frecuencia
Símbolo de la
magnitud
Τ
f, ν
frecuencia
angular
frecuencia
circular,
pulsantancia
longitud de onda
número de onda circular
ω
densidad
ρ
presión estática
Ps
presión acústica
P, (Pa)
λ
κ
Definición de la magnitud
Tiempo de un ciclo
Unidad SI
segundo
f = 1/T
hertz
El intervalo de frecuencia entre dos octava*
frecuencias es el logaritmo de la relación
entre la frecuencia más alta y la frecuencia
más baja
ω = 2πf
segundo recíproco
2π
κ = ------= 2πσ donde σ es el número
λ
de onda σ=1/λ
Masa dividida por el volumen
metro
metro recíproco
s
Símbolo de la unidad
SI
hz
s-1
m
m-1
kilogramo por metro kg/m3
cúbico
Presión que existiría en ausencia de ondas pascal
Pa
sonoras
La diferencia entre la presión total
instantánea y la presión estática
desplazamiento de una
ξ, (×)
Desplazamiento instantáneo de una metro
partícula de sonido
partícula del medio, referido a la posición
que ocuparía en ausencia de ondas sonoras
* Esta unidad no es del SI pero se acepta temporalmente su uso con el SI
m
NOM-008-SCFI-1993
35/74
Tabla 12 (Continuación)
velocidad
de
una
partícula de sonido
aceleración
de
una
partícula de sonido
gasto
volumétrico,
velocidad del volumen
velocidad del sonido
densidad de energía del
sonido
flujo de energía del
sonido, potencia del
sonido
intensidad del sonido
impedancia
característica
medio
de
impedancia
específica
acústica
un
u, ν
u = ∂ξ/∂t
a
a = ∂u/∂t
q, U
c, (ca)
w, (wa), (E)
P, (Pa)
I, J
Zc
Zs
metro por segundo
metro por segundo al
cuadrado
Razón instantánea de flujo de volumen metro cúbico por
debido a la onda sonora
segundo
Velocidad de una onda sonora
metro por segundo
La energía de sonido promedio en un joule por metro
volumen dado, dividida por dicho volumen cúbico
Energía del sonido transferida en un cierto watt
intervalo de tiempo, dividida por la
duración de ese intervalo
Para flujo unidireccional de energía de watt por metro
sonido, el flujo de energía de sonido a cuadrado
través de una superficie normal a la
dirección de propagación, dividido por el
área de esa superficie
Para un punto en un medio y una onda pascal segundo por
progresiva
plana,
la
representación metro
compleja de la presión de sonido dividida
por la representación compleja de la
velocidad de partícula
m/s
m/s2
m3/s
m/s
J/m3
W
W/m2
Pa·s/m
En una superficie, la representación
compleja de la presión de sonido dividida
por la representación compleja de la
velocidad de partícula
Tabla 12 (Continuación)
NOM-008-SCFI-1993
36/74
impedancia acústica
Za
impedancia mecánica
Zm
nivel de presión acústica
Lp
nivel
de
acústica
potencia
coeficiente
amortiguamiento
de
Lp, Lw
δ
En una superficie, la representación
compleja de la presión de sonido dividida
por la representación compleja de la razón
de flujo de volumen
La representación compleja de la fuerza
total aplicada a una superficie (o a un
punto) de un sistema mecánico, dividida por
la representación compleja de la velocidad
promedio de la partícula en esa superficie (o
de la velocidad de la partícula en ese punto)
en la dirección de la fuerza
Lp = 1n (p/po) = 1n 10·1g (p/po)
pascal segundo por
metro cúbico
Pa·s/m3
newton segundo por N·s/m
metro
decibel
dB
en donde p y po son respectivamente una
presión acústica y una presión de referencia
Lp= ½ 1n(p/po) = ½ 1n 10·1g(p/po)
decibel
dB
en donde p y po son respectivamente una
potencia acústica y una potencia de
referencia
Si una magnitud es una función del tiempo segundo recíproco
t, dada por F(t) = Ae-δt
s-1
F(t) = Ae-δt·sen ω(t-to)
entonces δ es
amortiguamiento
el
coeficiente
de
NOM-008-SCFI-1993
37/74
Tabla 12 (Continuación)
constante de tiempo,
tiempo de relajación
decrecimiento
logarítmico
coeficiente
de
atenuación
τ
Λ
α
τ = 1/δ donde δ es el coeficiente de segundo
amortiguamiento
Producto
del
coeficiente
de néper
amortiguamiento por el período
Si una magnitud es una función de la metro recíproco
distancia × y está dada por:
s
Np
F(×) = Ae-α× cos β(×-×ο)
entonces α es el coeficiente de atenuación y
β es el coeficiente de fase
coeficiente de fase
β
coeficiente
de
propagación
coeficiente de disipación
γ
coeficiente de reflexión
coeficiente
transmisión
de
coeficiente de absorción
acústica
γ = α + jβ
δ, (ψ)
Relación entre el flujo de energía acústica
disipado y el flujo de energía acústica
incidente
r, ρ
relación entre el flujo de energía acústica
reflejado y el flujo de energía acústica
incidente
τ
Relación entre el flujo de energía acústica
transmitido y el flujo de energía acústica
incidente
α, (αa)
α = δ+τ
Tabla 12 (Continuación)
NOM-008-SCFI-1993
38/74
índice de reducción
acústica, pérdida de
transmisión acústica
área
de
absorción
equivalente
de
una
superficie u objeto
tiempo de reverberación
nivel de sonoridad
R
A
T
LN
R= ½ 1n (1/τ) = ½ 1n 10·1g (1/τ)
decibel
en donde τ es el coeficiente de transmisión
Es el área de una superficie que tiene un metro cuadrado
coeficiente de absorción igual a 1, y que
absorbe la misma potencia en el mismo
campo sonoro difuso, considerando los
efectos de la difracción como despreciables
El tiempo que se requiere para que la segundo
densidad de energía de sonido promedio
dentro de un recinto cerrado disminuya
hasta 10-6 veces su valor inicial (o sea 60
dB), después de que la fuente ha dejado de
producir ondas sonoras
El nivel de sonoridad, en un punto de un fon*
campo sonoro, viene definido por:
dB
m2
s
Peff
LN = 1n ------------Po,eff 1 kHz
= 1n 10 · log (p eff/Po)1 kHz
en donde Peff es la presión acústica eficaz
(valor medio cuadrático) de un tono puro
normalizado de 1 kHz, que un observador
normal en condiciones de escucha
normalizada juzga igualmente sonoro que el
campo considerado, siendo Po = 2×10-5 Pa
= 20 µPa
NOM-008-SCFI-1993
39/74
Tabla 12 (Continuación)
sonoridad
N
La sonoridad es la estimación auditiva de un son*
observador normal de la relación entre la
intensidad del sonido considerado y el de un
sonido de referencia que tiene un nivel de
sonoridad de 40 fons
*Estas no son unidades del SI pero se acepta temporalmente su uso.
NOM-008-SCFI-1993
40/74
Tabla 13 Magnitudes y unidades de físico-química y físico-molecular
Magnitud
cantidad de substancia
constante de Avogadro
masa molar
volumen molar
energía interna molar
Símbolo de la
magnitud
n, (ν)
L,NA
M
Vm
Um, (Em)
capacidad térmica molar
Cm
entropía molar
Sm
densidad numérica de
moléculas
n
concentración molecular
de la substancia B
densidad
CB
concentración en masa
de la substancia B
ρB
ρ
Definición de la magnitud
Número de moléculas dividido por la
cantidad de substancia
NA = N/n= (6,022 045 ± 0,000 031) 1023 mol-1
Masa dividida por la cantidad de substancia
Volumen dividido por la cantidad de
substancia
Energía interna dividida por la cantidad de
substancia
Capacidad térmica dividida por la cantidad
de substancia
Entropía dividida por la cantidad de
substancia
El número de moléculas o partículas
dividido por el volumen
Unidad SI
mol (véase tabla 1)
mol recíproco
Símbolo de la unidad
SI
mol
mol-1
kilogramo por mol
kg/mol
metro cúbico por m3/mol
mol
joule por mol
J/mol
joule por mol kelvin
J/(mol·K)
joule por mol kelvin
J/(mol·K)
metro
recíproco
cúbico m-3
El número de moléculas de la substancia B
dividido por el volumen de la mezcla
Masa dividida por el volumen
kilogramo por metro kg/m3
cúbico
Masa de la substancia B dividida por el
volumen de la mezcla
Tabla 13 (Continuación)
NOM-008-SCFI-1993
41/74
concentración de la
substancia
B,
concentración de la
cantidad de la substancia
del componente B
molalidad
de
la
substancia soluto B
potencial químico de la
substancia B
cB
bB, mB
µB
Cantidad de substancia de componente B mol
por
dividida por el volumen de la mezcla
cúbico
metro mol/m3
La cantidad de substancia de soluto de la mol por kilogramo
substancia B en una solución dividida por la
masa del solvente
Para
una
mezcla
con
sustancias joule por mol
componentes B, C, ...
mol/kg
J/mol
µB = (∂G/∂nB) T, ρ,nc,...,
presión parcial de la
substancia B (en una
mezcla gaseosa)
fugacidad
de
la
substancia B (en una
mezcla gaseosa)
presión osmótica
PB
fB, PB
Π
donde nB es la cantidad de la substancia B;
y G es la entalpía libre
Para una mezcla gaseosa,
pascal
PB = ×B . P
donde la P es la presión
Para una mezcla gaseosa, fB es pascal
proporcional a la actividad absoluta B.
El factor de proporcionalidad, que es
función únicamente de la temperatura queda
determinado por la condición de que a
temperatura y composición constantes
fB/PB tiende a 1 para un gas infinitamente
diluido
El exceso de presión que se requiere para pascal
mantener el equilibrio osmótico entre una
solución y el solvente puro, separados por
una membrana permeable sólo para el
solvente
Pa
Pa
Pa
NOM-008-SCFI-1993
42/74
Tabla 13 (Continuación)
afinidad
(de
una
reacción química)
masa de una molécula
momento
dipolo
eléctrico
de
una
molécula
A
m
ρ, µ
polarizabilidad eléctrico
de una molécula
α
constante molar de los
gases
R
constante de Boltzmann
κ
trayectoria libre media
l, λ
coeficiente de difusión
D
coeficiente de difusión
térmica
DT
A = -ΣvB·µB
joule por mol
kilogramo
El momento de dipolo eléctrico de una coulomb metro
molécula es una magnitud vectorial cuyo
producto vectorial con la intensidad de
campo eléctrico es igual al par
Momento de dipolo eléctrico inducido coulomb
metro
dividido por la intensidad de campo cuadrado por volt
eléctrico
La constante universal de proporcionalidad joule por mol kelvin
en la ley de un gas ideal
pvm =RT
J/mol
kg
C·m
C·m2/V
J/mol·K
R = (8,314 41 ± 0,000 26) J/(mol·k)
κ = R/NA
joule por kelvin
J/K
κ = 1,380 662 ± 0,000 044× 10-23 J/K
Para una molécula, la distancia promedio metro
m
entre dos colisiones sucesivas
CB <VB> = -D grad CB
metro cuadrado por m2/s
segundo
donde CB es la concentración molecular
local del constituyente B en la mezcla y
<VB> es la velocidad media local de las
moléculas de B
DT = κT·D
metro cuadrado por m2/s
segundo
NOM-008-SCFI-1993
43/74
Tabla 13 (Continuación)
Número atómico
Z
Número de protones contenidos en el núcleo
de un elemento químico
carga elemental
e
La carga eléctrica de un protón
coulomb
La carga eléctrica de un electrón es igual a e
número de carga de un
ion, electrovalencia
constante de Faraday
z
F
fuerza iónica
I
e=(1,602 189 2 ± 0,000 004 6)×10-19 C
Coeficiente entre la carga de un ion y la
carga elemental
F = NAe
coulomb por mol
F = (9,648 456 ± 0,000 027 ×104 C/mol
mol por kilogramo
La fuerza iónica de una solución de define
como
C
C/mol
mol/kg
I = (1/2) Σzi2mi
donde la sumatoria incluye a todos los iones
con molalidad mi
conductividad
electrolítica
κ, σ
conductividad molar
Λm
La densidad de corriente electrolítica siemens por metro
S/m
dividida por la intensidad de campo
eléctrico
Conductividad
dividida
por
la siemens
metro S·m2/mol
concentración
cuadrado por mol
NOM-008-SCFI-1993
44/74
NOMBRES Y SÍMBOLOS DE LOS ELEMENTOS QUÍMICOS
Número atómico
1
2
Nombre
hidrógeno
helio
Símbolo
H
He
3
4
5
6
7
8
9
10
litio
berilio
boro
carbono
nitrógeno
oxígeno
flúor
neón
Li
Be
B
C
N
O
F
Ne
11
12
13
14
15
16
17
18
sodio
magnesio
aluminio
silicio
fósforo
azufre
cloro
argón
Na
Mg
Al
Si
P
S
Cl
Ar
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
potasio
calcio
escandio
titanio
vanadio
cromo
manganeso
hierro
cobalto
níquel
cobre
zinc, cinc
galio
germanio
arsénico
selenio
bromo
criptón
K
Ca
Sc
Ti
V
Cr
Mn
Fe
Co
Ni
Cu
Zn
Ga
Ge
As
Se
Br
Kr
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
rubidio
estroncio
itrio
circonio
niobio
molibdeno
tecnecio
rutenio
rodio
paladio
plata
cadmio
indio
estaño
antimonio
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
Pd
Ag
Cd
In
Sn
Sb
Número atómico
52
53
54
Nombre
teluro, telurio
yodo
xenón
Símbolo
Te
I
Xe
55
56
57
58
59
60
61
62
63
64
65
66
67
68
cesio
bario
lantano
cerio
praseodimio
neodimio
prometio
samario
europio
gadolinio
terbio
disprosio
holmio
erbio
Cs
Ba
La
Ce
Pr
Nd
Pm
Sm
Eu
Gd
Tb
Dy
Ho
Er
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
tulio
iterbio
lutecio
hafnio
tántalo, tantalio
volframio, wolframio
renio
osmio
iridio
platino
oro
mercurio
talio
plomo
bismuto
polonio
ástato
radón
Tm
Yb
Lu
Hf
Ta
W
Re
Os
Ir
Pt
Au
Hg
Tl
Pb
Bi
Po
At
Rn
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
francio
radio
actinio
torio
protactinio
uranio
neptunio
plutonio
americio
curio
berquelio
californio
einstenio
fermio
mendelevio
nobelio
lawrencio
Fr
Ra
Ac
Th
Pa
U
Np
Pu
Am
Cm
Bk
Cf
Es
Fm
Md
No
Lr
NOM-008-SCFI-1993
45/74
SÍMBOLO DE LOS ELEMENTOS QUÍMICOS Y DE LOS NUCLIDOS
Los símbolos de los elementos químicos deben escribirse en caracteres rectos. El símbolo no
va seguido de punto.
Ejemplos: H He C Ca
Los subíndices o superíndices que afectan al símbolo de los nuclidos o moléculas, deben tener
los siguientes significados y posiciones:
El número másico de un nuclido se coloca como superíndice izquierdo; por ejemplo:
14N
El número de átomos de un nuclido en una molécula se coloca en la posición del subíndice
derecho; por ejemplo:
14N2
El número atómico puede colocarse en la posición de subíndice izquierdo; por ejemplo:
64Gd
Cuando sea necesario, un estado de ionización o un estado excitado puede indicarse mediante
un superíndice derecho.
Ejemplos:
Estado de ionización:
Na+, PO3-4
Estado electrónico excitado. He*, NO*
Estado nuclear excitado:
110Ag* o bien 110Agm
NOM-008-SCFI-1993
46/74
ANEXO C
pH
El pH se define operacionalmente. Para una disolución X, se mide la fuerza electromotriz Ex
de la pila galvánica.
electrodo de referencia|disolución concentrada de KCl|disolución X|H2|Pt
y, análogamente, se mide la fuerza electromotriz de una pila galvánica que difiere de la
anterior únicamente en la sustitución de la disolución X de pH desconocido, designado por
pH(X), por una disolución patrón S, cuyo pH es pH(S). En estas condiciones,
pH (X) = pH(S) + (Es - Ex) F/(RT ln 10).
El pH así definido carece de dimensiones.
El Manual de la IUPAC sobre los símbolos y la terminología para las magnitudes y unidades
de química física (1979) da los valores de pH (S) para varias disoluciones patrón.
El pH no tiene un significado fundamental; su definición es una definición práctica. Sin
embargo, en el intervalo restringido de disoluciones acuosas diluidas que tienen
concentraciones en cantidad de sustancia inferiores a 0,1 mol/dm3 y no son ni fuertemente
ácidas ni fuertemente alcalinas (2 < pH < 12), la definición es tal que,
pH = -log10[c(H+)y1/(mol.dm-3)]± 0,02
donde c(H+) indica la concentración en cantidad de sustancia del ion hidrógeno H+ e y1
indica el coeficiente de actividad de un electrólito monovalente típico en la disolución.
NOM-008-SCFI-1993
47/74
Tabla 14 Magnitudes y unidades de físico atómica y nuclear
Magnitud
número
atómico,
número protónico
número neutrónico
número
nucleónico
número másico
masa del átomo
masa nuclídica
Símbolo de la
magnitud
Z
N
A
ma, m(X)
constante
de
masa
atómica (unificada)
Definición de la magnitud
Unidad SI
Símbolo de la unidad
SI
Número de protones contenidos en el núcleo
de un elemento químico
Número de neutrones contenidos en el
núcleo de un nuclido
Número de nucleones contenidos en el
núcleo de un nuclido
kilogramo
kg
Masa en reposo de un átomo en estado
fundamental
para el 1H
m(1H) = (1,673 559 4 ± 0,000 008 6)
×10-27 kg
=(1,007 825 036±0,000 000 011)u
unidad de masa u*
1/12 de la masa en reposo de un átomo atómica (unificada)
neutro del nuclido 12C en el estado
fundamental
mu = (1,660 565 5±0,000 008 6)×10-27 kg
= 1 u*
ma
---- se llama masa nuclídica relativa
mu
masa (en reposo) del
electrón
me
me = (0,910 953 4±0,000 004 7)×10-30 kg
= (5,485 802 6±0,000 002 1)×10-4 u*
mp = (1,672 648 5±0,000 008 6)×10-27 kg
masa (en reposo) del
mp
protón
= (1,007 276 470±0,000 000 011) u*
* Esta unidad no es del SI pero se permite su uso temporalmente.
kilogramo
kg
NOM-008-SCFI-1993
48/74
Tabla 14 (Continuación)
masa (en reposo) del
neutrón
carga elemental
constante de Plank
mn
mn = (1,674 954 3 ± 0,000 008 6)×10-27 kg
= (1,008 665 012 ± 0,000 000 037) u
e
La carga eléctrica de un protón es:
h
e = (1,602 189 2±0,000 004 6)×10-19 C
Cuanto elemental de acción
kilogramo
unidad de
atómica
coulomb
masa
kg
u
C
h = (6,626 176±0,000 036)×10-34 J.s
h = h/2π
= (1,054 588 7±0,000 005 7)×10-34 J.s
radio de Bohr
ao
4π εο h2
ao = --------------me e2
metro
m
metro recíproco
m-1
joule
J
ao = (0,529 177 06±0,000 000 44)×10-10m
constante de Rydberg
energía de Hartree
Rω
Eh
e2
Rω = ---------------8π εο aοhc
= (1,097 373 177±0,000 000 083)
× 107 m-1
Eh = e24πεοaο = 2Rω.hc
= 4,359 81 × 10-18 J
momento magnético de
una partícula o núcleo
µ
magnetón de Bohr
µB
magnetón nuclear
µN
coeficiente
giromagnético
giromagnética)
(razón
γ
factor g del átomo o del
electrón
g
factor g del núcleo o de
la partícula nuclear
g
frecuencia angular de
Larmor
(frecuencia
circular de Larmor)
ωL
frecuencia angular de
precesión nuclear
ωN
NOM-008-SCFI-1993
49/74
Tabla 14 (Continuación)
Valor
medio
del
componente ampere
electromagnético en la dirección del campo cuadrado
magnético
en
el
estado
cuántico
correspondiente al número cuántico
magnético máximo
metro A·m2
eh
µB = -------- = (9,274 078 ± 0,000 036)
2me
× 10-24 A·m2
e
me
µN = ------- = ----- µB = (5,050 824
2mp
mp
± 0,000 020)
× 10-27 A·m2
µ
γ = ---Jh
ampere
metro A·m2/(J.s)
cuadrado por joule
segundo
en donde J es el número cuántico del
momento angular
µB
e
γ = -g ----- = - g --h
2me
µN
e
γ = - g ----- = - g --h
2mp
e
ωL = -------- B
2me
donde B es la densidad de flujo magnético
ωN = γB
segundo recíproco
s-1
NOM-008-SCFI-1993
50/74
Tabla 14 (Continuación)
frecuencia
angular
ciclotrónica (frecuencia
circular ciclotrónica)
momento cuadrupolar
nuclear
radio nuclear
número cuántico de
momento
angular
orbital, número cuántico
secundario,
número
cuántico acimutal
número cuántico de
espín
número cuántico de
espín total
número cuántico de
espín nuclear
ωC
Q
q
ωc = ---- B
m
q
donde ----- es la razón de carga a la
m masa de la partícula y B es la
densidad de flujo magnético
Valor esperado de la magnitud
segundo recíproco
s-1
metro cuadrado
m2
(1/e) ∫ (3z2-r2 ρ (x, y, z) dxdydz
R
li, L
si , S
ji, J
I
en el estado cuántico con el espín nuclear en
la dirección (Z) del campo; ρ (x, y, z) es la
densidad de carga nuclear y "e" es la carga
elemental
El radio promedio del volumen en el que la metro
materia nuclear es incluida
m
NOM-008-SCFI-1993
51/74
Tabla 14 (Continuación)
número cuántico de
estructura hiperfina
número
cuántico
principal
número
cuántico
magnético
radio del electrón
F
n
mi, M
re
e2
re = -------------4π εo mec2
metro
m
metro
m
longitud de onda de
Comptón
λc
= 2,817 938 0±0,000 007 0 ×10-15 m
λc = 2πh/mc = h/mc
exceso de masa
∆
donde m es la masa en reposo de la
partícula
∆ = ma - Amu
kilogramo
defecto de masa
B
B = Zm(1H)+Nmn-ma
exceso relativo de masa
∆r
∆r = ∆/mu
Br
Br = B/mu
defecto relativo de masa
fracción
empaquetamiento
de
fracción
de
enlace,
energía de enlace por
nucleón
f
f = ∆r/A
b
b = Br/A
kg
NOM-008-SCFI-1993
52/74
Tabla 14 (Continuación)
vida promedio
τ
ancho de nivel
Γ
actividad
(radiactividad)
A
actividad específica en
una muestra
a
constante
desintegración,
constante
decaimiento
λ
de
de
Para decaimiento exponencial, el tiempo
promedio requerido para reducir el número
N de átomos o núcleos de un estado
específico hasta N/e
h
Γ = --τ
El número promedio de transiciones
nucleares espontáneas ocurridas en una
cierta cantidad de un radionuclido dentro de
un corto intervalo de tiempo, dividido por el
valor de ese intervalo
La actividad de un nuclido radioactivo
presente en una muestra, dividida por la
masa total de la muestra
La constante de decaimiento es la
probabilidad de decaimiento en un pequeño
intervalo de tiempo dividido por este
intervalo.
segundo
s
joule
J
becquerel
Bq
becquerel
kilogramo
por Bq/kg
segundo recíproco
s-1
Para decaimiento exponencial
vida media
T½
dN
---- = - λ N
dt
donde N es el número de átomos radiactivos
en el tiempo t y λ = 1/τ
Para declinación exponencial, el tiempo segundo
promedio requerido para la desintegración
de la mitad de los átomos de una muestra de
un nuclido radiactivo
s
NOM-008-SCFI-1993
53/74
Tabla 14 (continuación)
energía
desintegración alfa
de
Qα
energía máxima
partícula beta
energía
desintegración beta
de
Eβ
de
Qβ
La suma de la energía cinética de la joule
partícula α producida en el proceso de
desintegración y la energía residual del
átomo producido en el marco de referencia
en que el núcleo emisor está en reposo antes
de su desintegración
La energía máxima del espectro de energía joule
en un proceso de desintegración beta
La suma de la energía máxima de partícula joule
beta Eβ y la energía residual del átomo
producido en el marco de referencia en que
el núcleo emisor se encuentra en reposo
antes de su desintegración
J
J
J
NOM-008-SCFI-1993
54/74
Tabla 15 Magnitudes y unidades de reacciones nucleares ionizantes
Magnitud
energía de reacción
energía de resonancia
sección transversal
sección transversal total
sección
angular
transversal
Símbolo de la
magnitud
Q
Er, Rres
σ
σtot, σT
σΩ
Definición de la magnitud
Unidad SI
En una reacción nuclear, la suma de las joule
energías cinéticas y radiante de los
productos de la reacción, menos la suma de
las energías cinética y radiante de los
reactivos.
La energía cinética de una partícula joule
incidente, en el marco de la referencia del
objetivo, correspondiente a una resonancia
en una reacción nuclear
Para una entidad objetivo especificada y metro cuadrado
para una reacción o proceso especificado
por partículas incidentes cargadas o
descargadas de energía y tipo especificado,
la sección transversal es el cociente de la
probabilidad de esta reacción o proceso para
esta entidad objetivo y la fluencia de
partícula de las partículas incidentes
J
Símbolo de la unidad
SI
J
m2
La suma de todas las secciones
transversales correspondientes a las diversas
reacciones o procesos ocurridos entre la
partícula incidente y la partícula objetivo
Sección transversal necesaria para disparar metro cuadrado por m2/sr
o dispersar una partícula dentro de un esterradián
elemento de ángulo sólido, dividido por
dicho elemento
σ = ∫ σΩdΩ
NOM-008-SCFI-1993
55/74
Tabla 15 (Continuación)
sección
espectral
transversal
σE
Sección transversal para un proceso en el metro cuadrado por m2/J
que la energía de la partícula disparada o joule
dispersada está en un elemento de energía,
dividida por ese elemento
σ = ∫σEdE
sección
transversal
angular espectral
sección
transversal
macroscópica, densidad
de sección transversal
sección
transversal
macroscópica
total,
densidad de sección
transversal total
fluencia de partícula
σΩ, E
Σ
Σtot, ΣT
Φ
Sección transversal necesaria para disparar metro cuadrado por m2/(sr.J)
o dispersar una partícula dentro de un esterradián joule
elemento de ángulo sólido, con energía en
un elemento de energía, dividida por el
producto de estos dos elementos
σ = ∫∫ σΩ, EdΩdE
La suma de las secciones transversales de metro recíproco
una reacción o proceso de un tipo
específico, para todos los átomos de un
volumen dado, dividida por ese volumen
La suma total de las secciones transversales
para todos los átomos en un volumen dado,
dividido por ese volumen
En un punto dado del espacio, el número de metro
partículas incidentes sobre una pequeña recíproco
esfera en un intervalo de tiempo, dividido
por el área de la sección transversal de esa
esfera
m-1
cuadrado m-2
NOM-008-SCFI-1993
56/74
Tabla 15 (Continuación)
tasa de fluencia de
partículas, densidad de
flujo de partículas
fluencia de energía
tasa de fluencia de
energía, densidad de
flujo de energía
densidad de corriente de
partículas
ϕ
ψ
ψ
J, (S)
µ, µ
coeficiente
atenuación lineal
de
coeficiente
atenuación másica
coeficiente
atenuación molar
de
µ/ρ, µm
de
µc
dφ
ϕ = ---dt
En un punto dado en el espacio, la suma de
las energías, excluyendo la energía en
reposo, de todas las partículas incidentes
sobre una pequeña esfera en un intervalo de
tiempo, dividida por el área seccional
transversal de esa esfera
dψ
ψ = ---dt
La integral de una magnitud vectorial cuya
componente normal sobre cualquier
superficie, es igual al número "neto" de
partículas pasando a través de esa superficie
en un pequeño intervalo de tiempo, dividido
por ese intervalo
dJ/d× = -µJ
donde J es la densidad de corriente de un
haz de partículas paralelo a la dirección ×
El coeficiente de atenuación lineal dividido
por la densidad de masa de la substancia
µc = µ/c, donde c es la concentración de
cantidad de substancia
joule por
cuadrado
metro
recíproco
recíproco
metro J/m2
cuadrado m-2.s-1
segundo
metro recíproco
m-1
metro cuadrado por m2/kg
kilogramo
metro cuadrado por m2/mol
mol
NOM-008-SCFI-1993
57/74
Tabla 15 (Continuación)
coeficiente
atenuación atómica
de
espesor medio, valor
medio de espesor, capa
hemirreductora
potencia de detención
lineal total, poder de
frenado lineal total
µa, µat
d1/2
S , S1
potencia de detención
atómica total, poder de
frenado atómico total
Sa
potencia de detención
másica total, poder
frenado másico total
alcance lineal medio
S/ρ, (Sm)
alcance másico medio
Rρ, (Rm)
R , R1
µa = µ/n
metro cuadrado
donde n es la densidad numérica de átomos
en la substancia
El espesor de la capa atenuadora que reduce metro
la densidad de corriente de un haz
unidireccional a la mitad de su valor inicial
Para una partícula cargada ionizante de joule por metro
energía E, moviéndose en la dirección ×
S = -dE/d×
Sa = S/n
donde n es la densidad numérica de átomos
en la substancia
La potencia de detención lineal total
dividida por la densidad de masa de la
substancia
La distancia que una partícula penetra en
una substancia dada, bajo condiciones
específicas promediadas de un grupo de
partículas que tiene la misma energía
El alcance lineal medio multiplicado por la
densidad de masa de la substancia
m2
m
J/m
joule metro cuadrado J.m2
joule metro cuadrado J.m2/kg
por kilogramo
metro
m
kilogramo por metro kg/m2
cuadrado
NOM-008-SCFI-1993
58/74
Tabla 15 (Continuación)
ionización lineal por una
partícula
Nil
pérdida promedio de
energía por par de iones
formados
movilidad
Wi
densidad numérica de
iones, densidad de iones
n+, n-
coeficiente
recombinación
de
µ
α
densidad numérica de
neutrones
n
rapidez del neutrón
densidad de flujo de
neutrones, rapidez de
flujo de neutrones
υ
ϕ
El número de cargas elementales del mismo
signo, producidas en un elemento de la
longitud de la trayectoria de una partícula
cargada ionizante dividido por ese elemento
La energía cinética inicial de una partícula
cargada ionizante, dividida por la ionización
total de esa partícula
La velocidad de arrastre promedio impartida
por un campo eléctrico o una partícula
cargada en un medio, dividido por la
intensidad del campo
El número de iones positivos o negativos de
un elemento de volumen, dividido por ese
elemento
Coeficiente en la Ley de recombinación
dn+ dn--- ----- = ------ = αn+ndt
dt
El número de neutrones libres en un
elemento de volumen, dividido por ese
elemento
La magnitud de la velocidad neutrónica
En un punto dado en el espacio, el número
de neutrones incidentes sobre una pequeña
esfera, en un pequeño intervalo de tiempo,
dividido por el área de sección transversal
de esa esfera y por el intervalo de tiempo
metro recíproco
m-1
joule
J
metro cuadrado por m2/(V.s)
volt segundo
metro
recíproco
cúbico m-3
metro cúbico
segundo
metro
recíproco
por m3/s
cúbico m-3
metro por segundo
m/s
segundo
recíproco s-1.m-2
metro
cuadrado
recíproco
NOM-008-SCFI-1993
59/74
Tabla 15 (Continuación)
coeficiente de difusión,
coeficiente de difusión
para
la
densidad
numérica de neutrones
D, Dn
J× = -Dn∂n/∂×
coeficiente de difusión
para la densidad de flujo
de neutrones, coeficiente
de difusión para rapidez
de fluencia de neutrones
densidad total de una
fuente de neutrones
Dϕ, (D)
donde J× es la componente × de la densidad
de corriente de neutrones y n es la densidad
numérica de neutrones
J× = -Dϕ∂ϕ/∂×
metro
S
densidad de frenado
q
probabilidad de escape a
la resonancia
p
letargía
u
donde J× es la componente × de la densidad
de corriente neutrónica y es la densidad de
flujo neutrónico
Razón de la producción de neutrones en un
elemento de volumen, dividido por ese
elemento
La densidad numérica de neutrones
retardados, pasando un valor de energía
dado, durante un corto intervalo de tiempo,
dividida por dicho intervalo
En medio infinito, probabilidad de que un
neutrón, al frenarse a través de una zona
energética donde existen resonancias, la
rebase sin ser absorbido
En el frenado de neutrones, logaritmo
neperiano del cociente entre una energía de
referencia Eo, normalmente la máxima del
neutrón, y la que este posee, E
metro cuadrado por m2/s
segundo
segundo
metro
recíproco
segundo
metro
recíproco
m
recíproco s-1.m-3
cúbico
recíproco s-1.m-3
cúbico
NOM-008-SCFI-1993
60/74
Tabla 15 (Continuación)
decaimiento logarítmico
medio
trayectoria
promedio
libre
ξ
1, λ
L2s, L2s1
área de retardamiento
área de difusión
L2
área de migración
m2
longitud
retardamiento
de
Ls, Ls1
longitud de difusión
L
longitud de migración
M
Valor medio de la disminución del
logaritmo neperiano de la energía de los
neutrones en sus condisiones elásticas con
núcleos cuya energía
cinética
es
despreciable comparada con la de los
neutrones
La distancia promedio que viaja una metro
partícula entre dos reacciones o procesos
específicos sucesivos
En un medio homogéneo infinito, la sexta metro cuadrado
parte de la distancia cuadrática media entre
la fuente de un neutrón y el punto donde el
neutrón alcanza una energía determinada
m
m2
En un medio homogéneo infinito, la sexta
parte de la distancia cuadrática media entre
el punto donde el neutrón entra a una clase
especificada y el punto donde abandona esta
clase
La suma del área de retardamiento de
energía de fisión a energía térmica y el área
de difusión para neutrones térmicos
La raíz cuadrada del área de retardamiento metro
m
La raíz cuadrada del área de difusión
La raíz cuadrada del área de migración
NOM-008-SCFI-1993
61/74
Tabla 15 (Continuación)
ν
rendimiento neu-trónico
de la absorción
En la fisión de un nuclido determinado,
promedio del número de neutrones, lo
mismo inmediatos que diferidos, emitidos
en cada fisión
η
factor de fisión rápida
ε
factor de
térmica
utilización
f
de
Λ
Promedio del número de neutrones de
fisión, lo mismo inmediatos que diferidos,
emitido por cada neutrón que se absorbe en
un nuclido fisionable o en un combustible
nuclear, según se especifique
Para un medio infinito, razón entre el
número medio de neutrones producidos por
todas las fisiones y el de neutrones
producidos exclusivamente por las fisiones
térmicas
Para un medio infinito, razón entre el
número de neutrones térmicos absorbidos
en un combustible nuclear, según se
especifique, y el número total de neutrones
térmicos absorbidos
Probabilidad de que un neutrón no escape
del núcleo de un reactor durante el proceso
de moderación o el de difusión en la zona
térmica
Para un medio multiplicativo, razón entre el
número total de neutrones producidos
durante un intervalo de tiempo y el número
total de neutrones perdidos por absorción y
escape durante el mismo intervalo
rendimiento neutrónico
de la fisión
probabilidad
permanencia
factor de multiplicación
k
NOM-008-SCFI-1993
62/74
Tabla 15 (Continuación)
factor de multiplicación
infinito,
factor
de
multiplicación de un medio
infinito
kω
Factor de multiplicación de un medio sin fugas
neutrónicas
factor de multiplicación
efectivo
reactividad
keff
constante de tiempo del
reactor
T
actividad
A
energía impartida
ε
Factor de multiplicación correspondiente a un
medio finito
En un medio multiplicativo, medida de la
desviación entre el estado del medio y su estado
crítico
keff -1
ρ = -------------keff
El tiempo requerido para que la densidad de segundo
flujo neutrónico de un reactor cambie en un
factor "e" cuando la densidad de flujo aumenta
o disminuye exponencialmente
El número promedio de transacciones nucleares becquerel
espontáneas ocurridas en una cierta cantidad de
un radionuclido, dentro de un corto intervalo de
tiempo, dividido por el valor de ese intervalo
La energía impartida por radiación ionizante a la joule
materia en un volumen, es, la diferencia entre la
suma de las energías de todas las partículas
directamente
ionizantes
(cargadas)
e
indirectamente ionizantes (sin carga) que han
ocupado el volumen y la suma de las energías
de todas aquellas que han salido de él, menos la
energía equivalente de cualquier incremento de
la masa en reposo que tenga lugar en reacciones
de partículas elementales o nucleares
ρ
s
Bq
J
NOM-008-SCFI-1993
63/74
Tabla 15 (Continuación)
energía impartida media
energía
impartida
específica
ε
z
dosis absorbida
D
equivalente de dosis
H
rapidez
de
dosis
absorbida
transferencia lineal de
energía
D
kerma
k
L
El promedio de la energía impartida
joule
Para cualquier radiación ionizante la energía gray
impartida a un elemento de materia
irradiada, dividida por la masa de ese
elemento
Para cualquier radiación ionizante, la
energía media impartida a un elemento de
materia irradiada, dividida por la masa de
este elemento
El equivalente de dosis es el producto de
DQ, y N en el punto de interés, donde D es
la dosis absorbida, Q es el factor de calidad
y la N es el producto de otros factores
determinantes cualesquiera
Dosis absorbida en un pequeño intervalo de
tiempo, dividida por este intervalo
Para una partícula cargada ionizante, la
energía local impartida a una masa, a través
de una pequeña distancia, dividida por esa
distancia
Para partículas indirectamente ionizantes
(sin carga), la suma de las energías cinéticas
iniciales de todas las partículas cargadas
liberadas en un elemento de materia,
dividida por la masa de ese elemento
J
Gy
sievert
Sv
gray por segundo
Gy/s
joule por metro
J/m
gray
Gy
NOM-008-SCFI-1993
64/74
Tabla 15 (Continuación)
rapidez de kerma
coeficiente
de
transferencia de energía
másica
k
µtr/ρ
kerma en un pequeño intervalo de tiempo, gray por segundo
Gy/s
dividido por ese intervalo
Para un haz de partículas indirectamente metro cuadrado por m2/kg
ionizante (sin cargas)
kilogramo
k
µtr = --ψ
exposición
x
rapidez de exposición
X
donde ψ es la densidad de flujo de energía
Para radiación X o gamma, la carga
eléctrica total de los iones del mismo signo
producidos cuando todos los electrones
liberados (negativos y positivos) por fotones
en un elemento de aire son detenidos en el
aire, dividida por la masa de ese elemento
Exposición en un pequeño intervalo de
tiempo, dividida entre ese intervalo
coulomb
kilogramo
por C/kg
coulomb
por C/(kg.s)
kilogramo segundo
NOM-008-SCFI-1993
65/74
5
UNIDADES QUE NO PERTENECEN AL SI
Existen algunas unidades que no pertenecen al SI, por ser de uso común, la CGPM las ha
clasificado en tres categorías:
unidades que se conservan para usarse con el SI;
unidades que pueden usarse temporalmente con el SI.
unidades que no deben utilizarse.
5.1
Unidades que se conservan para usarse con el SI.
Son unidades de amplio uso, por lo que se considera apropiado conservarlas; sin embargo, se
recomienda no combinarlas con las unidades del SI para no perder las ventajas de la
coherencia, la relación de estas unidades se establecen en la Tabla 16.
5.2
Unidades que pueden usarse temporalmente
Son unidades cuyo empleo debe evitarse, se mantienen temporalmente en virtud de su gran
uso actual, pero se recomienda no emplearlas conjuntamente con las unidades SI, la relación
de estas unidades se establece en la Tabla 17.
5.3
Unidades que no deben utilizarse
Existen otras unidades que no pertenecen al SI; actualmente tienen cierto uso, algunas de
ellas derivadas del sistema CGS, dichas unidades no corresponden a ninguna de las categorías
antes mencionadas en esta Norma por lo que no deben utilizarse en virtud de que hacen
perder la coherencia del SI; se recomienda utilizar en su lugar, las unidades respectivas del SI.
En la tabla 18 se dan algunos ejemplos de estas unidades.
6
PREFIJOS
La Tabla 19 contiene la relación de los nombres y los símbolos de los prefijos para formar los
múltiplos y submúltiplos decimales de las unidades, cubriendo un intervalo que va desde 1024 a 1024.
7
REGLAS GENERALES PARA LA ESCRITURA DE LOS SÍMBOLOS DE LAS
UNIDADES DEL SI
Las reglas para la escritura apropiada de los símbolos de las unidades y de los prefijos, se
establecen en la Tabla 20.
8
REGLAS PARA LA ESCRITURA DE LOS
DECIMAL
NÚMEROS Y SU SIGNO
La Tabla 21 contiene estas reglas de acuerdo con las recomendaciones de la Organización
Internacional de Normalización (ISO).
NOM-008-SCFI-1993
66/74
TABLA 16 Unidades que no pertenecen al SI, que se conservan para
usarse con el SI
Magnitud
tiempo
ángulo
volumen
masa
trabajo, energía
masa
Unidad
minuto
hora
día
grado
minuto
segundo
Símbolo
min
h
d
°
'
"
equivalente
1 min = 60 s
1 h = 60 min 3 600 s
1 d =24 h = 86 400 s
1° = (π/180) rad
1' = (π/10 800) rad
1" = (π/648 000) rad
l, L
lL = 10-3 m3
t
1t = 103 kg
electronvolt
eν
1eV = 1,602 19 x 10-19 J
unidad de masa
atómica
u
1 u = 1,660 57 x 10-27 kg
litro
tonelada
NOM-008-SCFI-1993
67/74
Tabla 17 Unidades que no pertenecen al SI que pueden usarse
temporalmente con el SI
Magnitud
Unidad
área
hectárea
barn
Símbolo
a
ha
b
Equivalencia
1a = 102 m2
1ha = 104 m2
1b = 10-28 m2
longitud
angströn
Å
1Å = x 10-10 m
longitud
milla náutica
presión
bar
superficie
velocidad
nudo
dosis de
radiación
röntgen
dosis
absorbida
radiactividad
1 milla náutica = 1852 m
bar
1 bar = 105 Pa
1nudo = (1852/3 600) m/s
R
1R =2,58 x 10-4 C/kg
rad*
rad (rd)
1 rad = 10-2 Gy
curie
Ci
1 Ci = 3,7 x 1010 Bq
aceleración
gal
Gal
1 gal = 10-2 m/s2
equivalente
de dosis
rem
rem
1 rem = 10-2 Sv
* El rad es una unidad especial empleada para expresar dosis absorbida de radiaciones
ionizantes. Cuando haya riesgo de confusión con el símbolo del radián, se puede emplear rd
como símbolo del rad.
NOM-008-SCFI-1993
68/74
Tabla 18 Ejemplos de unidades que no deben utilizarse
Magnitud
Unidad
longitud
fermi
longitud
unidad x
volumen
stere
Símbolo
equivalencia
fm
10-15 m
unidad X
1,002 X 10-4 nm
st
1 m3
masa
quilate métrico
CM
2 X 10-4 kg
fuerza
kilogramo-fuerza
kgf
9,806 65 N
presión
torr
energía
caloría
cal
4,186 8 J
fuerza
dina
dyn
10-5 N
energía
erg
erg
10-7 J
luminancia
stilb
sb
104 cd/m2
viscosidad
dinámica
viscosidad
cinemática
poise
P
0,1 Pa.s
stokes
St
10-4 m2/s
luminosidad
phot
ph
104 1x
inducción
intensidad campo
magnético
gauss
Gs, G
10-4 T
oersted
Oe
(1000/4 π) A/m
flujo magnético
inducción
masa
volumen
maxwell
gamma
gamma
lambda
Mx
10-8 Wb
10-9 T
10-9 kg
10-9 m3
133,322 Pa
NOM-008-SCFI-1993
69/74
Tabla 19 Prefijos para formar múltiplos y submúltiplos
Nombre
yotta
zetta
exa
peta
tera
giga
mega
kilo
hecto
deca
deci
centi
mili
micro
nano
pico
femto
atto
zepto
yocto
Símbolo
Y
Z
E
P
T
G
M
k
h
da
d
c
m
µ
n
p
f
a
z
y
1024
1021
1018
1015
1012
109
106
103
102
101
10-1
10-2
10-3
10-6
10-9
10-12
10-15
10-18
10-21
10-24
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Valor
1 000 000 000 000 000 000 000 000
1 000 000 000 000 000 000 000
1 000 000 000 000 000 000
1 000 000 000 000 000
1 000 000 000 000
1 000 000 000
1 000 000
1 000
100
10
0,1
0,01
0,001
0,000 001
0,000 000 001
0,000 000 000 001
0,000 000 000 000 001
0,000 000 000 000 000 001
0,000 000 000 000 000 000 001
0,000 000 000 000 000 000 000 001
NOM-008-SCFI-1993
70/74
Tabla 20 Reglas generales para la escritura de los símbolos de las unidades del SI
1
Los símbolos de las unidades deben ser expresados en caracteres romanos, en
general, minúsculas, con excepción de los símbolos que se derivan de nombres
propios, en los cuales se utilizan caracteres romanos en mayúsculas
Ejemplo: m, cd, K, A
2
No se debe colocar punto después del símbolo de la unidad
3
Los símbolos de las unidades no deben pluralizarse
Ejemplos: 8 kg, 50 kg, 9 m, 5 m
4
El signo de multiplicación para indicar el producto de dos ó más unidades debe
ser de preferencia un punto. Este punto puede suprimirse cuando la falta de
separación de los símbolos de las unidades que intervengan en el producto, no se
preste a confusión
Ejemplos: N.m o Nm, también m.N pero no: mN que se confunde con
milinewton, submúltiplo de la unidad de fuerza, con la unidad de momento de
una fuerza o de un par (newton metro)
5
Cuando una unidad derivada se forma por el cociente de dos unidades, se puede
utilizar una línea inclinada, una línea horizontal o bien potencias negativas
Ejemplos: m/s o ms-1
para designar la unidad de velocidad: metro por segundo
6
No debe utilizarse más de una línea inclinada a menos que se agreguen
paréntesis. En los casos complicados, deben utilizarse potencias negativas o
paréntesis
Ejemplo: m/s2 ó m.s-2, pero no: m/s/s
m.kg/(s3.A) ò m.kg.s-3 .A-1, pero no: m.kg/s3/A
NOM-008-SCFI-1993
71/74
Tabla 20 (Continuación)
7
Los múltiplos y submúltiplos de las unidades se forman anteponiendo al nombre
de éstas, los prefijos correspondientes con excepción de los nombres de los
múltiplos y submúltiplos de la unidad de masa en los cuales los prefijos se
anteponen a la palabra "gramo"
Ejemplos: dag, Mg (decagramo; megagramo)
ks, dm (kilosegundo; decímetro)
8
Los símbolos de los prefijos deben ser impresos en caracteres romanos (rectos),
sin espacio entre el símbolo del prefijo y el símbolo de la unidad
Ejemplos: mN (milinewton) y no: m N
9
Si un símbolo que contiene a un prefijo está afectado de un exponente, indica que
el múltiplo de la unidad está elevado a la potencia expresada por el exponente
Ejemplos: 1 cm3 = (10-2 m)3 = 10-6 m3
1 cm-1 = (10-2 m)-1 = 102 m-1
10
Los prefijos compuestos deben evitarse
Ejemplo: 1 nm (un nanómetro)
pero no: 1 mµm (un milimicrómetro)
NOM-008-SCFI-1993
72/74
Tabla 21 Reglas para la escritura de los números y su signo decimal
Los números deben ser generalmente impresos en tipo romano. Para facilitar la
lectura de números con varios dígitos, estos deben ser separados en grupos
apropiados preferentemente de tres, contando del signo decimal a la derecha y a
la izquierda, los grupos deben ser separados por un pequeño espacio, nunca con
una coma, un punto, o por otro medio.
Signo decimal El signo decimal debe ser una coma sobre la línea (,). Si la magnitud de un
número es menor que la unidad, el signo decimal debe ser precedido por un cero.
Números
NOM-008-SCFI-1993
73/74
9
BIBLIOGRAFÍA
- Le Systeme International d'Unités (SI)
Bureau international des Poids et Measures.
Pavillon de Breteuil, F-92310 Sévres France 1985
- Recueil de Travaux du Bureau International des Pois et Measures
Volumen 2, 1968-1970.
Bureau International des Pois et Measures. Pavillon de
Breteuil. 92310 Sevres, Francia.
- ISO 1000 (1981)
SI units and recommendations for the use of use of their multiples and
of certain others certain other units.
- ISO 31/O (1981)
General principles concerning quantities, units and symbols.
- ISO 31/1 (1978)
Quantities and units of space and time.
- ISO 31/II (1978)
Quantities and units of periodic and related related phenomens.
- ISO 31/III (1978)
Quantities and units of mechanics.
- ISO 31/IV (1978)
Quantities and units of heat.
- ISO 31/V (1979)
Quantities and units of electricity and magnetism.
- ISO 31/6 (1980)
Quantities and units of light and related electromagnetic radiations.
- ISO 31/VII (1978) Quantities and units of acoustics.
- ISO 31/8 (1980)
Quantities and units of physical chemistry and and molecular physics.
- ISO 31/9 (1980)
Quantities and units of atomic and nuclear physics.
- ISO 31/10-1980
Quantities and units of nuclear reactions and and ionizing radiations.
- NFXO2-201-1985 Grandeurs, unites ete symboles d'espace et de temps.
- NFXO2-202-1985
Grandeurs, unités et symboles de phénoménes phénoménes periodiques
et connexes.
- NFXO2-203-1985 Grandeurs, unités et symboles de mécanique.
- NFXO2-204-1985 Grandeurs, unités et symboles de thermique.
- NFXO2-205-1985 Grandeurs, unités et symboles d'electicité et de magnétisme.
NOM-008-SCFI-1993
74/74
- NFXO2-206-1985
Grandeurs, unités et symboles des rayonnements electro magnétiques et
d'optique.
- NFXO2-207-1985 Grandeurs, unités et symboles d'acoustique.
- NFXO2-208-1985
Grandeurs, unités et symboles de chimie physique et de physique
moléculaire.
- NFXO2-209-1985 Grandeurs, unités et symboles de phyusique atomique et nucleaire.
10
CONCORDANCIA CON NORMAS INTERNACIONALES
Esta norma concuerda con lo establecido en los documentos del Bureau International des
Poids et Mesures y las normas ISO mencionadas en la Bibliografía. Las tablas se han
estructurado eligiendo las unidades más usuales.
México, D. F. a
EL DIRECTOR GENERAL DE NORMAS
LIC. LUIS GUILLERMO IBARRA
ALL/GLA/JCM/lgd