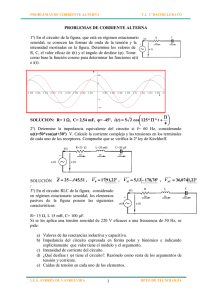
i(t) u u u R L=0,025 H C=50 µF u(t)=120*√2 *cos(400*t) ω ω
Anuncio

PROBLEMAS DE CORRIENTE ALTERNA 4º) En el circuito de la figura i(t) esta adelantada 45º respecto a la tensión. Calcular el valor de R y las tensiones eficaces e instantáneas en los terminales de cada elemento. R i(t) L=0,025 H + uR C=50 µF uL uC u(t)=120*√2 *cos(400*t) SOLUCIÓN La tensión de la fuente en forma simbólica es: V = 120 0º Las impedancias de la bobina y el condensador son: X L = jωL = j 400 * 0,0025 = j10 Ω XC = − j j =− = − j 50 Ω ωC 400 * 50 * 10 − 6 Por tanto la reactancia del circuito es: X = X L + X C = − j 40 Ω Como el enunciado nos dice que la corriente está adelantada 45º a la tensión, de ahí, podemos saber que el circuito tiene carácter capacitivo (i adelantada) y que la reactancia del circuito es igual a la resistencia del mismo (45º), en definitiva: j XL = j L UR = R*I =45º R = X = 40 Ω -j X C = - j 1 Z Z = 40 + j 40 = 40 * 2 45º Ω I= I 120 0º V 3 = 45º A = Z 40 * 2 45º 2 A partir de aquí únicamente necesitamos calcular las tensiones en los terminales de cada uno de los elementos del circuito: Se comprueba que tensión y corriente 3 120 U R = R * I = 40 * 45º = 45º V en los terminales de la resistencia están en 2 2 fase. U L = X L * I = j10 * 3 30 45º = 135º V 2 2 U C = X C * I = − j 50 * 3 150 45º = − 45º V 2 2 I.E.S. ANDRÉS DE VANDELVIRA En los terminales de la bobina la tensión va adelantada 90º a la corriente. En los terminales del condensador la tensión va atrasada 90º a la intensidad DEPARTAMENTO DE TECNOLOGÍA C PROBLEMAS DE CORRIENTE ALTERNA Con las expresiones simbólicas anteriores, establecemos sus funciones temporales: u R ( t ) = 120 * cos (400t + 45º ) V u L ( t ) = 30 * cos (400t + 135º ) V u R ( t ) = 150 * cos (400t− 45º ) V Diagrama vectorial de las tensiones y triángulo de tensiones. eje imag. 45° ω UR UC U U eje real 45° 135 ° 45° UL UL UR UC Aún que no lo pide calcularemos todas las potencias del circuito: La potencia activa consumida por el circuito vista desde el generador es: P = V * I * cos ϕ = 120 * 3 2 3 * cos (ϕ U − ϕ i ) = 120 * 2 * cos ( − 45º ) = 120 * 3 2 * 2 = 180W 2 Dado que únicamente existe una resistencia, la potencia activa del circuito será la que consuma la propia resistencia, lo que se puede comprobar como: 2 3 PR = R * I = 40 * = 180 W 2 2 La potencia reactiva que absorbe el circuito visto desde el generador es: Q = V * I * sen ϕ = 120 * 3 2 * sen ( −45º ) = 120 * 2 = − 180 VAr * − 2 2 3 lo que nos indica que el circuito es generador de reactiva. Otra forma de obtener la potencia reactiva del circuito es calculando la potencia reactiva de bobina y condensador y sumándolas: 2 3 Reactiva consumida por la bobina: Q L = X L * I = 10 * = 45VAr 2 2 2 3 Reactiva aportada por el condensador: QC = X C * I = −50 * = −225 VAr 2 2 I.E.S. ANDRÉS DE VANDELVIRA DEPARTAMENTO DE TECNOLOGÍA PROBLEMAS DE CORRIENTE ALTERNA La reactiva del circuito es: Q = Q L + QC = 45 − 225 = −180 VAr Otra forma alternativa de calcular las potencias del circuito es a través de la potencia aparente: La potencia aparente del circuito demandada por el circuito visto desde el generador es: S = V * I * = 120 * como S = P + jQ P = 180W Q = −180VAr 3 2 − 45º = 360 2 − 45º = 180 − j180 , concluimos TRIÁNGULO DE POTENCIAS QL 45° P QC S I.E.S. ANDRÉS DE VANDELVIRA DEPARTAMENTO DE TECNOLOGÍA