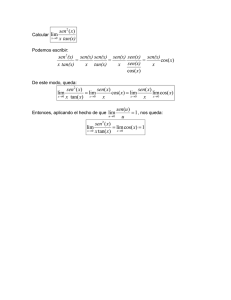
Chapter 2 review, problem 77. Evaluate lim √ 1 + tan x − √ 1 + sin x
Anuncio

Chapter 2 review, problem 77. √ √ 1 + tan x − 1 + sin x . Evaluate lim x→0 x3 Solution. √ √ √ √ √ √ 1 + tan x − 1 + sin x 1 + tan x − 1 + sin x 1 + tan x + 1 + sin x √ √ lim = lim x→0 x→0 x3 x3 1 + tan x + 1 + sin x [ multiply by conjugate of numerator ] = lim x→0 x3 (1 + tan x) − (1 + sin x) √ √ 1 + tan x + 1 + sin x √ √ [ let w = 1 + tan x + 1 + sin x to save space ] (1 + tan x) − (1 + sin x) x→0 x3 w tan x − sin x = lim x→0 x3 w sin x − sin x cos x = lim cos x 3 cos x [ rewrite tan x, find common denominator ] x→0 x w = lim = lim x→0 sin x−sin x cos x cos x x3 w sin x − sin x cos x x3 w cos x (sin x)(1 − cos x) [ factor out sin x ] = lim x→0 x3 w cos x (sin x)[2 sin2 (x/2)] = lim x→0 x3 w cos x [ from half-angle formula sin2 θ = (1 − cos 2θ)/2, with θ = x/2 ] = lim x→0 (sin x)[2 sin2 (x/2)] [ rewrite denominator ] x→0 4x(x/2)2 w cos x 2 2 sin x sin(x/2) 1 [ pull apart ] = lim x→0 4 x x/2 w cos x 2 sin x sin(x/2) 1 1 lim lim lim = x→0 x→0 w cos x 2 x→0 x x/2 [ product rule for limits ] = lim 1 1 (1)(1)2 lim x→0 w cos x 2 1 1 √ = lim √ 2 x→0 1 + tan x + 1 + sin x cos x ! 1 1 √ √ = 2 1 + tan 0 + 1 + sin 0 cos 0 ! 1 1 √ √ = 2 1 + 0 + 1 + 0 (1) = = 1 . 4 [ since lim x→0 sin x = 1] x [ back-substitute w ] [ plug in x = 0 ]