b xD xC e h1 h2 a w -6 ? ? ? ? ? ? a ? ? ? ? xD 0 ? ? ? h2 0 ? ? ?
Anuncio

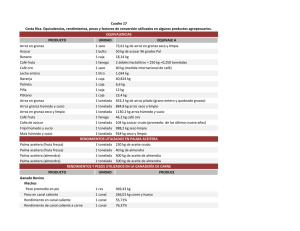
Primer Examen Parcial Optimización I Curso 2011-12 / Matemática / Semestre 5 / 24 de octubre de 2011 Nombre: 1. La empresa fabricante de productos lácteos “La Vaquita” produce un variado surtido de estos, consideraremos sólo dos de estos productos: leche condensada (LC) y leche evaporada (LE). El proceso de producción de la leche, cualquiera sea su tipo, se realiza completamente en alguno de los tres departamentos: A, B y C. Como el director de la empresa sabe que usted tiene buenos conocimientos de PL, le pide formular un modelo matemático que permita determinar cuál debe ser el surtido de producción diario de estos dos productos de manera que se maximice el valor de la producción diaria. Las cantidades a producir de estos dos productos están sujetas a las siguientes consideraciones: 1. En el departamento A se producen ambos productos y su capacidad está medida de la siguiente forma: si sólo se produce LC la capacidad es de 500 toneladas (t) diarias y si sólo se produjera LE, la capacidad asciende a 750 t diarias. 2. En el departamento B sólo se procesa LC y su capacidad es de 400 t diarias, mientras que en el departamento C sólo se procesa LE su capacidad asciende a 450 t diarias. 4. La materia prima fundamental es la leche fresca. El consumo de leche fresca en la producción de LC y LE es de 0.3 y 1.3 t respectivamente por tonelada de producto terminado. La cantidad de leche fresca disponible en la fábrica diariamente es de 650 t. 5. A ambos tipos de leche se le adiciona vitamina D, siendo el requerimiento de vit D por tonelada de LC el doble del correspondiente a la LE. Esta vitamina se adiciona en una proporción de 54 kg por tonelada de LC, siendo su disponibilidad de 24750 kg diarios. 6. Se demanda una cantidad mixta de estos productos, y la política de producción más conveniente es elaborar al menos una tonelada de LC por cada tres toneladas de LE. 7. El producto terminado se vende al precio de $ 200 la tonelada de LC y $300 la tonelada de LE. 2. En un supermercado se promociona una marca de queso desconocida D utilizando una marca conocida C, y se hace la siguiente oferta: "Pague sólo a $p el kg de queso C y a $1 el kg de quesoD siempre y cuando: (*) xD + xC 6 // obligación mínima de compra (kg) xD - 2xC 0 // política de equilibrio i) -2xD + xC 0 // política de equilibrio ii) xD , xC 0 // xD y xC representan las cantidades a comprar (en kg) de queso de marca D y C . 2.1 Represente gráficamente los modos de acogerse a la oferta, suponiendo ilimitado el capital disponible. 2.2 ¿Cuáles son las combinaciones de kg de queso de tipo D y C que hacen mínima la cantidad total que usted puede llevar? Detalle una solución básica óptima, relaciónela con alguno de los puntos extremos. ¿cuáles son las variables básicas?, ¿y las no básicas? 2.3. La siguiente tabla corresponde a la aplicación del Simplex en su fase I para el SEL (*), las variables adicionales e, h1 y h2 fueron utilizadas en la estandarización-en ese orden-, en tanto a1 es artificial. w a xD h2 b -6 ? 0 0 xD ? ? ? ? xC ? e ? h1 ? 3 -2 -3 -1 0 0 -1 1 2 h2 ? ? ? ? a ? ? ? ? 2.3.1 Complete los espacios ocupados por el signo “?”, fundamente. 2.3.2 Si el coeficiente de e en la fila de la función objetivo fuera distinto entonces w alcanzaría el valor de 2, ¿por qué? 2.3.3 Describa completamente la tabla Simplex a utilizar en la fase II. 2.4 Resuelva, por Simplex, a partir de la tabla lograda en el inciso anterior, el problema de minimizar el costo de la compra, dependiendo del valor en oferta para el queso de tipo C.