grandezas e unidades de medida

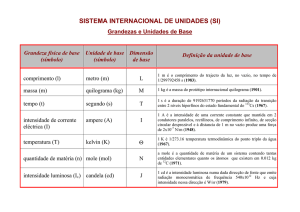
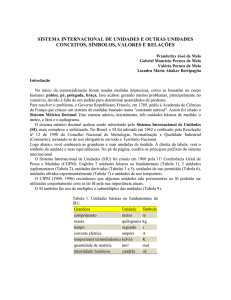
GOVERNO DO ESTADO DO RIO DE JANEIRO
FUNDAÇÃO DE APOIO À ESCOLA TÉCNICA – FAETEC
ESCOLA TÉCNICA ESTADUAL SANTA CRUZ – ETESC
DISCIPLINA DE QUÍMICA
Profs.: Ana Cristina, Denis Dutra e José Lucas
Ano Letivo: 2010
GRANDEZAS E UNIDADES DE MEDIDA *
Uma grandeza é um atributo de uma coisa do universo físico que pode ser quantificado (medido).
A medida de uma grandeza consiste sempre na comparação da sua magnitude (valor numérico) com
aquela de uma outra usada como referência. Toda grandeza utilizada como referência é denominada unidade
de medida, e sua magnitude é completamente arbitrária.
Assim, o valor (magnitude) de uma grandeza é igual ao produto de um valor numérico e uma unidade:
grandeza = valor numérico x unidade
1. SISTEMAS DE UNIDADES
Um conjunto amplo de unidades de medida, bem como as regras que as definem e as relacionam,
caracteriza-se como um sistema de unidades, no passado denominado de pesos e medidas.
A maioria das unidades consuetudinárias (decorrentes de costume, sem qualquer planejamento) foram
estabelecidas de modo absolutamente independente umas das outras. Sistemas de unidades modernos, ao
contrário, têm como uma de suas principais características um relacionamento entre as unidades de diferentes
grandezas. Essas relações são determinadas através de leis da natureza ou de definições pré-determinadas.
Num sistema deste último tipo, as unidades de determinadas grandezas, consideradas como totalmente
independentes entre si, são escolhidas para servir de base ao sistema (as unidades de base) e todas as
outras unidades são obtidas a partir dessas (as unidades derivadas).
UNIDADES E PADRÕES DE MEDIR
Unidades de medida existem com o objetivo principal de se padronizar a medida de grandezas. Para que
este objetivo possa ser atingido, faz-se necessária a disponibilidade de padrões de medir. Padrões de medir
são objetos construídos com elevado grau de perfeição, destinados a materializar a magnitude de uma dada
grandeza, em geral a própria unidade de medida desta grandeza.
No caso de unidades de medida para comprimento ou distância, medidas corporais provavelmente foram
as referências mais convenientes e usadas nos tempos antigos, como se observa no caso da polegada, do pé,
da jarda (comprimento do braço) ou da milha (equivalente a mil passadas duplas). As primeiras unidades de
massa e volume, provavelmente, derivaram casualmente do uso de certos recipientes, ou a partir de
estimativas daquilo que um homem ou animal poderia levantar ou carregar.
No século XVII, cientistas europeus vinham apontando a necessidade de um novo sistema de medidas,
que fosse racional e uniforme, para substituir os vários sistemas nacionais, que com suas diferenças
*
Adaptado de ROCHA-FILHO, R.C. GRANDEZAS E UNIDADES DE MEDIDA. O Sistema Internacional de Unidades.
Editora Ática, 1988.
FAETEC/ETESC
Grandezas Químicas
2
dificultavam a comunicação científica. Tal sistema pôde finalmente surgir com a Revolução Francesa, no final
do século XVIII.
Por recomendação da Academia Francesa de Ciências, adotou-se corno unidade de comprimento o
metro, definido como a décima milionésima parte da distância do Pólo Norte ao Equador pelo meridiano que
passa por Paris, e como seu padrão a distância entre duas marcas numa barra de platina. O grama, unidade
básica de massa, foi tomado como igual à massa de um centímetro cúbico de água na temperatura de sua
o
máxima densidade (4 C); fabricou-se um cilindro de platina, conhecido como o Quilograma dos Arquivos, e
este foi declarado como o padrão para 1000 gramas. Além disso, o mais importante é que se adotou um
sistema decimal, tendo sido proposta uma lista de prefixos para múltiplos e submúltiplos das unidades criadas.
2. O SISTEMA INTERNACIONAL DE UNIDADES
O Sistema Internacional de Unidades, normalmente referido simplesmente como SI, compreende três
tipos de unidades: unidades SI de base, unidades SI derivadas e unidades SI suplementares. Essas três
classes formam um conjunto de unidades coerente, isto é, um sistema de unidades mutuamente relacionadas
por regras de multiplicação e divisão, sem o envolvimento de quaisquer fatores numéricos (constantes de
proporcionalidade) além de 1. O SI também compreende uma série de prefixos (atualmente 16) que permitem
a formação de múltiplos e submúltiplos das unidades. Em adição, existem algumas poucas unidades que não
são SI mas cujo uso é permitido junto com as SI.
UNIDADES DE BASE
As sete unidades SI de base são aquelas a partir das quais todo o sistema é construído. A tabela a
seguir contém uma listagem destas sete unidades SI de base.
TABELA 1 – Unidades SI de base e grandezas relacionadas.
Grandeza
Unidade
Símbolo
Grandeza
Unidade
Símbolo
Comprimento
metro
m
Temperatura termodinâmica
kelvin
K
Massa
quilograma
kg
Quantidade de matéria
mol
mol
Tempo
segundo
s
Intensidade luminosa
candela
cd
Corrente elétrica
ampère
A
O ampère é usado em eletricidade, o kelvin em termodinâmica, o mol em química e a candela em ótica.
O quilograma é a única unidade de base que contém um prefixo no seu nome, já que o grama foi considerado
muito pequeno para este propósito. Apesar da unidade de temperatura termodinâmica ser o kelvin, no dia-a-dia
usa-se o grau Celsius, unidade de medida de temperatura Celsius. A relação entre as unidades de temperatura
termodinâmica (T) e Celsius (t) é:
TIK = tIC +273,16
UNIDADES DERIVADAS
Multiplicando-se uma unidade de base por si mesma ou associando-se duas ou mais unidades de base
através de simples multiplicação e/ou divisão, pode-se obter um amplo conjunto de unidades denominadas
unidades SI derivadas. Assim, por exemplo, a unidade SI derivada de densidade é obtida dividindo-se um
3
quilograma por um metro cúbico, resultando o quilograma por metro cúbico, kg/m .
FAETEC/ETESC
Grandezas Químicas
3
TABELA 2 – Algumas unidades SI derivadas simples.
Grandeza
Unidade
Símbolo
Área
metro quadrado
m
2
Volume
metro cúbico
m
3
Densidade
quilograma por metro cúbico
kg/m
Concentração em quantidade de matéria
mol por metro cúbico
mol/m
3
3
TABELA 3 – Nomes e símbolos especiais para algumas unidades SI derivadas.
Grandeza
Nome da unidade SI
Símbolo
Pressão
Pascal
Pa
Energia
Joule
J
Potência
Watt
W
Carga elétrica
Coulomb
C
Diferença de potencial
Temperatura
Volt
V
o
grau Celsius
Definição
-1
m kg s
–2
2
(= N/m )
–2
2
m kg s
(= N.m)
–3
2
m kg s
(= J/s)
sA
–3
2
–1
m kg s
A
C
(= W/A)
K
UNIDADES OUTRAS USADAS COM AS SI
Existem algumas unidades de medida alheias ao SI (Tabela 4) que são tão amplamente difundidas que
fazem parte do nosso dia-a-dia. Por terem este papel tão importante no cotidiano, o CIPM (1969) optou por
mantê-las em uso juntamente com as unidades SI.
TABELA 4 – Unidades em uso com aquelas do SI.
Unidade
Símbolo
Valor em unidade SI
Litro
l ou L
0,001 m
Tonelada
t
1000 kg
elétron-volt
eV
Unidade de massa atômica
u
3
1,602177 x 10
1,66054 x 10
–19
–27
J
kg
Note que o símbolo para litro pode ser tanto l como L. O símbolo L para litro configura-se como uma
exceção à regra que reza que símbolos com letras maiúsculas só devem ser utilizados para nomes de unidades epônimos de nomes próprios, por razões tipográficas (evitar-se confundir o número 1 com o símbolo l).
PREFIXOS SI
O SI foi estabelecido de modo que as magnitudes de quaisquer grandezas possam ser expressas em
termos de alguma(s) de suas unidades. Entretanto, em muitos casos, suas unidades acabam sendo demasiadamente grandes ou pequenas. Para evitar o uso de números expressos de forma muito longa, o SI contém
prefixos que permitem a formação de múltiplos e submúltiplos decimais de suas unidades. Assim, a distância
desde o Sol até Plutão é expressa como 6 Tm (seis terametros), isto é, 6 x 10
12
m (ou 6 000 000 000 000 m), e
-6
a massa da asa de uma abelha como 50 g (cinqüenta microgramas), isto é, 50 x 10 g (ou 0,000 000 05 kg).
FAETEC/ETESC
Grandezas Químicas
4
TABELA 5 – Prefixos SI.
Prefixo
Símbolo
Fator pelo qual a unidade é multiplicada
exa
E
1 000 000 000 000 000 000
= 1018
peta
P
1 000 000 000 000 000
= 1015
tera
T
1 000 000 000 000
= 1012
giga
G
1 000 000 000
= 109
mega
M
1 000 000
= 106
quilo
k
1 000
= 103
hecto
h
100
= 102
deca
da
10
= 101
1
= 100
deci
d
0,1
= 10–1
centi
c
0,01
= 10–2
mili
m
0,001
= 10–3
0,000 001
= 10–6
micro
nano
n
0,000 000 001
= 10–9
pico
p
0,000 000 000 001
= 10–12
femto
f
0,000 000 000 000 001
= 10–15
atto
a
0,000 000 000 000 000 001
= 10–18
3. DEFINIÇÕES DAS UNIDADES SI DE BASE E SUPLEMENTARES
As definições das unidades SI de base estão constantemente sob análise visando aumentar a precisão
do padrão de cada unidade e da sua reprodutibilidade nos diferentes laboratórios nacionais de padrões. Abaixo
estão listadas algumas das definições mais recentes de cada uma das unidades SI de base.
Metro: comprimento do caminho percorrido pela luz, no vácuo, durante o intervalo de tempo de
a
1/299792458 de segundo (17 CGPM – 1983).
a
a
Quilograma: massa do protótipo internacional do quilograma (1 CGPM – 1889; 3 CGPM – 1901).
Segundo: duração de 9 192 631 770 períodos da radiação correspondente à transição entre os dois níveis
a
hiperfinos do estado fundamental do átomo de césio 133 (13 CGPM – 1967).
a
Kelvin: fração (1/273,16) da temperatura termodinâmica do ponto tríplice da água (13 CGPM – 1967).
Mol: 1) quantidade de matéria de um sistema que contém tantas entidades elementares quantos são os
átomos contidos em 0,012 quilograma de carbono 12;
2) quando se utiliza o mol, as entidades elementares devem ser especificadas, podendo ser átomos,
a
moléculas, íons, elétrons, outras partículas ou agrupamentos de tais partículas (14 CGPM – 1971).
4. REGRAS BÁSICAS DE ESTILO
REGRAS PARA A GRAFIA E A PLURALIZAÇÃO DE NOMES DE UNIDADES
Quando escritos por extenso, os nomes de unidades começam por letra minúscula, mesmo quando são
epônimos de nomes de cientistas, exceto no caso do grau Celsius. Exemplos: ampère, kelvin, newton, etc.
Na expressão da magnitude de uma grandeza, a respectiva unidade pode ser escrita por extenso ou
representada por seu símbolo. Não se deve, entretanto, representar a unidade combinando partes por extenso
com partes expressas por símbolo. Exemplo:
km/h
ou
quilômetro por hora
e não
km/hora
ou
quilômetro/h
FAETEC/ETESC
Grandezas Químicas
5
A pluralização dos nomes das unidades, quando escritos por extenso ou pronunciados, deve obedecer
às seguintes regras:
1) Os prefixos SI são sempre invariáveis (não se usam quilos, centis, milis, megas, etc.).
2) Ao plural do nome de uma unidade só se adiciona a letra s (exceto nos casos da regra 3) de modo a não
desfigurar o nome que a unidade tem no singular. Assim, tem-se:
a) palavras simples: newtons, ampères, grays, becquerels, mols, pascals, volts, etc.
b) palavras compostas em que o elemento complementar de um nome da unidade não está ligado a
este por hífen: metros cúbicos, centímetros quadrados, unidades astronômicas, etc.
c) termos compostos por multiplicação, em que os componentes podem variar independentemente um
do outro: watts-horas, newtons-metros, ampères-horas, etc.
3) Aos nomes ou partes dos nomes de unidades não se adiciona a letra s no final, quando:
a) terminam pelas letras s, x ou z; por exemplo: lux, hertz, siemens, etc.
b) correspondem ao denominador de unidades derivadas obtidas por divisão: joules por mol, metros por
segundo, watts por esterradiano, etc.
c) são, em palavras compostas, elementos complementares de nomes de unidade e a estes ligados por
hífen ou preposição: unidades (unificadas) de massa atômica, elétron-volts, etc.
REGRAS PARA A GRAFIA E O USO DOS SÍMBOLOS DE UNIDADES SI
1) Os símbolos para unidades SI devem ser expressos em tipos redondos (romanos), em geral minúsculos
(m, para metro, por exemplo). Entretanto, quando o nome da unidade é derivado de um nome próprio, a
primeira letra do símbolo é maiúscula (N, para newton).
2) Os símbolos das unidades permanecem inalterados no plural (10 m, e não 10 ms).
3) Os símbolos das unidades não são seguidos por ponto, a não ser no final de uma frase.
SOBRE O USO DOS ADJETIVOS ESPECÍFICO(A) E MOLAR
Diversas grandezas têm suas magnitudes dependentes da massa e da quantidade de matéria presentes
no corpo ou amostra; grandezas deste tipo são denominadas de extensivas. Por exemplo, o volume de um
corpo qualquer é diretamente proporcional à massa desse corpo e à sua quantidade de matéria. Em outras
palavras, à medida que a massa e a quantidade de matéria do corpo aumentam o volume também aumenta, à
medida que aquelas diminuem este também diminui. O adjetivo especifico(a) qualificando o nome de uma
grandeza extensiva indica a magnitude desta grandeza por unidade de massa, ou seja, essa grandeza dividida
pela massa.
Exemplo:
volume (V)

volume específico (v)

v = V/m
O adjetivo molar qualificando o nome de uma grandeza extensiva indica a magnitude desta grandeza por
unidade de quantidade de matéria, ou seja, esta grandeza dividida pela quantidade de matéria. O símbolo da
grandeza molar é o mesmo da respectiva grandeza extensiva acrescido do subíndice m, exceto no caso da
massa molar, cujo símbolo é M.
Exemplos:
volume (V)

volume molar (Vm)

Vm = V/n
massa (m)

massa molar (M)

M = m/n
FAETEC/ETESC
Grandezas Químicas
6
ALGUNS ERROS COMUNS QUE DEVEM SER EVITADOS
É errado...
O correto é...
utilizar símbolos de unidades seguidos de ponto.
Errado: h., min.
usar o ponto após o símbolo de uma unidade se este for o
último termo de uma frase. Correto: h, min
usar grau centígrado como unidade de temperatura Celsius. usar o nome grau Celsius.
Errado: 100 graus centígrados
Correto: 100 graus Celsius
representar o símbolo do prefixo quilo como K maiúsculo.
Errado: Kg (para quilograma)
usar-se o k minúsculo.
Correto: kg
utilizar símbolos para unidades SI diferentes dos oficiais.
Errado: Mt ou Mts ou mt ou mts para símbolo de metro
usar apenas o símbolo oficial.
Correto: m (para a unidade metro)
no caso de unidades epônimas de nomes de cientistas, escrever o nome da unidade usando letra inicial minúscula
escrever o nome da unidade usando-se letra inicial (porém, o símbolo destas unidades sempre começa por letra
maiúscula. Errado: 320 Kelvins
maiúscula). Correto: 320 kelvins (320 K)
pronunciar como ponto a vírgula que separa a parte inteira usar a vírgula para separa a parte inteira de um número da
de um número da decimal (ou pior, grafar o número usando- parte decimal.
se ponto em vez de vírgula). Errado: dois ponto cinco (2.5)
Correto: dois vírgula cinco (2,5)
no caso específico do centímetro cúbico usar, erroneamente, deixar de lado tais representações e sempre usar o símbolo
3
3
os símbolos cc ou c.c. Errado: motor com 125 cc
recomendado, cm . Correto: motor com 125 cm
denominar o submúltiplo do metro, micrômetro, como Utilizar, corretamente, a unidade micrômetro e o símbolo
mícron ou micra, e representá-lo por μ ou u.
μm.
Correto: 200 micrômetros (200 μm)
Errado: 200 mícrons (200 u)
a referência à unidade de temperatura termodinâmica a 13ª CGPM (1967) decidiu que estes nomes deveriam ser
como sendo o grau Kelvin ou, às vezes, o grau.
abandonados em favor de simplesmente kelvin.
Errado: quarenta graus Kelvins
Correto: quarenta kelvins
denominar a temperatura cuja unidade de medida é o kelvin, usar o termo correto, temperatura termodinâmica.
erradamente, de temperatura absoluta.
chamar de peso a grandeza cuja unidade é o quilograma.
Errado: o peso líquido
o quilograma é a unidade de medida da grandeza massa.
Correto: a massa líquida
5. FATORES DE CONVERSÃO
O entendimento do que é um fator de conversão é facilitado pela resolução do seguinte problema, usual
no dia-a-dia: "Quantos mililitros existem em 3,5 litros, sabendo-se que uma hora contém 1000 militros?". A
resposta a esta questão pode ser encontrada através da resolução de uma simples regra de três:
1 L — 1000 mL
3,5 L — v

v = 3,5 L x 1000 mL = 3500 mL
1L
, ou
v = 3,5 L x 1000 mL = 3500 mL
1L
(note que a unidade L se cancela)
Esse problema configura-se numa simples conversão de unidade para a grandeza volume, isto é,
conversão da unidade litro na unidade mililitro. Na realidade, sabe-se que, por definição: 1 L = 1000 mL. Essa
igualdade matemática (relação entre duas unidades diferentes de uma mesma grandeza) pode ser dividida, em
ambos os lados, por outro volume qualquer, sem deixar de ser uma igualdade. Assim, se for dividida por 1 litro
obtém-se:
1 L = 1000 mL
1L
1L
mas,
1L = 1
1L
portanto,
1000 mL = 1
1L
isto é, o quociente (1000 mL/1 L) corresponde à identidade (é igual a um). Entretanto, note que na resolução do
problema inicialmente proposto, este quociente multiplica o volume em litros para se obter o volume em
mililitros, isto é, o volume expresso em litros está sendo multiplicado pela identidade e, como conseqüência, é
convertido em volume em mililitros. Daí que a entidade – nesse caso o quociente (1000 mL/1 L) – faz o papel
de um fator de conversão.