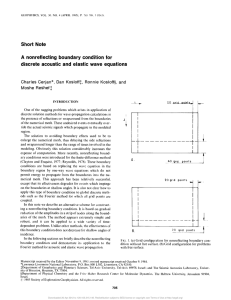
Continuous-discontinuous modelling of failure based on non
Anuncio

Universitat Politècnica de Catalunya Programa de Doctorat de Matemàtica Aplicada Departament de Matemàtica Aplicada III Continuous-discontinuous modelling of failure based on non-local displacements by Elena Tamayo-Mas Thesis Proposal Advisor: Antonio Rodrı́guez-Ferran Barcelona, July 2010 Abstract Continuous-discontinuous modelling of failure based on non-local displacements Elena Tamayo-Mas Two different kinds of approaches are typically used to model failure of quasibrittle materials: (a) damage mechanics and (b) fracture mechanics. The former, which belongs to the family of continuous models, is able to capture damage inception and its diffuse propagation. The latter, which falls in the family of discontinuous models, can be used to model the final stages of failure processes, when the body is physically separated in two or more parts. In order to achieve a better description of the entire failure process, integrated strategies which combine these two traditional approaches have recently emerged. In this work, a new contribution in this direction is presented: a non-local continuum damage model based on non-local displacements is used to simulate the initial stages of failure whereas it is coupled to a discontinuous model to capture crack initiation and its propagation. iii Contents Abstract iii Contents v List of Figures vii List of Tables xi List of Symbols xiii Latin symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xiii Greek symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xiv Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xv 1 Introduction 1.1 Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2 Layout of the proposal . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 State of the art 2.1 Continuum failure models . . . . . . . . . . . . . . . . . 2.1.1 Continuum damage models . . . . . . . . . . . . 2.2 Discontinuous failure models . . . . . . . . . . . . . . . . 2.2.1 Cohesive crack models . . . . . . . . . . . . . . . 2.2.2 Computational modelling of strong discontinuities 2.3 Continuous-discontinuous failure models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Continuous model of failure based on non-local displacements 3.1 Gradient continuous non-local damage model . . . . . . . . . . . . 3.2 Boundary conditions for the regularisation equation . . . . . . . . 3.3 Numerical examples: validation of the model . . . . . . . . . . . . 3.3.1 Square plate under mode I loading conditions . . . . . . . 3.3.2 Single-edge notched beam . . . . . . . . . . . . . . . . . . 3.4 Concluding remarks . . . . . . . . . . . . . . . . . . . . . . . . . . v . . . . . . . . . . . . . . . . . . . . . . . . 1 1 2 . . . . . . 5 5 6 10 11 12 18 . . . . . . 21 22 22 27 28 30 33 4 Continuous-discontinuous model based on non-local displacements 4.1 Gradient continuous-discontinuous non-local damage model . . . . . . . 4.1.1 Problem fields . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.1.2 Governing equations . . . . . . . . . . . . . . . . . . . . . . . . 4.1.3 Variational formulation . . . . . . . . . . . . . . . . . . . . . . . 4.1.4 Discretised and linearised weak governing equations . . . . . . . 4.2 Finite element technology . . . . . . . . . . . . . . . . . . . . . . . . . 4.2.1 Introducing a discontinuity . . . . . . . . . . . . . . . . . . . . . 4.2.2 Orienting a discontinuity . . . . . . . . . . . . . . . . . . . . . . 4.3 Numerical examples: validation of the model . . . . . . . . . . . . . . . 4.3.1 2D uniaxial tension test . . . . . . . . . . . . . . . . . . . . . . 4.3.2 Square plate under mode I loading conditions . . . . . . . . . . 4.4 Concluding remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 42 42 43 45 47 50 50 51 52 52 54 57 5 Future work 61 6 Publications 65 Bibliography 71 vi List of Figures 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.1 3.2 3.3 3.4 3.5 Kinematic description with (a) strong discontinuity; (b) weak discontinuity and (c) no discontinuities. . . . . . . . . . . . . . . . . . . . . . Cohesive crack process zone. . . . . . . . . . . . . . . . . . . . . . . . . Different cohesive laws used in the literature: (a) linear with secant unloading (b) bilinear and (c) exponential laws. . . . . . . . . . . . . . The three fracture modes: (a) Mode I or opening mode (b) Mode II or sliding mode and (c) Mode III or tearing mode. . . . . . . . . . . . . . The mesh conforms to crack geometry. . . . . . . . . . . . . . . . . . . Triangular element crossed by a crack (embedded discontinuity model). A crack line (dashed line) in a structured mesh with standard elements (white), elements whose nodes are all enriched (dark grey) and blending elements (light grey). Nodes in J and K are indicated by circles and squares respectively. Adapted from Moës et al. (1999). . . . . . . . . . Polar coordinates used to evaluate the tip enrichment functions. . . . . Subdomain quadrature: the elements cut by the crack are subdivided into subdomains (dashed lines). . . . . . . . . . . . . . . . . . . . . . . x) = ua (x, y) = 1 + Validation test with (a) a linear source term ua (x x + 5y. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. . . . . . . . . . . . . . . . . . . . . . . Validation test with (a) a tent function source term. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Validation test with (a) a tent function source term. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Square plate under mode I loading conditions: problem statement. . . . Square plate under mode I loading conditions. Four meshes with different element density and different imperfection sizes are used. . . . . vii 10 11 11 12 13 14 16 17 18 26 27 28 29 30 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13 Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: damage profiles with deformed meshes (×100). . . . . . . . . . . . . . . . . . . . . . . Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: force-displacement curves. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Single-edge notched beam: problem statement. All distances in mm. . SENB reference test. Four meshes with different element density are used. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . √ SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: final damage profiles. . . . . . . . . . . . . . . . . . . √ SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: force-displacement curves. . . . . . . . . . . . . . . . SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: force-displacement curves. . . . . . . . . . . . . . . . SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: final damage profiles. . . . . . . . . . . . . . . . . . . . 31 . 32 . 32 . 36 . 37 . 38 . 38 . 39 4.1 Notations for a body with a crack subjected to loads and imposed displacements. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.2 Constitutive law for the cracked bulk: (a) elastic unloading with D = Dcrit ; (b) linear traction-separation law for the crack. . . . . . . . . . . 4.3 Sketch of the cohesive tip region. A crack line (dashed line) in a mesh with standard elements (white) and elements whose nodes are enriched (grey). Enriched nodes with H = +1 and H = −1 are indicated by squares and circles respectively. . . . . . . . . . . . . . . . . . . . . . . 4.4 Determination of the propagation direction: the crack propagates according to the direction perpendicular to the isolines of the damage field. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.5 Uniaxial tension test: problem statement. . . . . . . . . . . . . . . . . . 4.6 Evolution law for (a) the bar; (b) the crack. . . . . . . . . . . . . . . . √ 4.7 Uniaxial tension test. Fixed characteristic length ` = 5 with various meshes. (a) force-displacement curve; (b) damage profiles. . . . . . . . 4.8 Uniaxial tension test. Fixed mesh with various characteristic lengths. (a) force-displacement curve; (b) damage profiles. . . . . . . . . . . . . 4.9 Uniaxial tension test. Fixed mesh and characteristic length with various imperfection sizes. (a) force-displacement curve; (b) damage profiles. 4.10 Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: damage profiles with deformed meshes (×100). . . . . . . . . . . . . . . . . . . . . . . . viii 42 51 51 52 53 53 54 55 55 56 4.11 Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: force-displacement curves. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 5.1 5.2 Work schedule. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 Representation of the branching. . . . . . . . . . . . . . . . . . . . . . . 63 ix List of Tables 2.1 2.2 2.3 Generic equations of a local damage model. . . . . . . . . . . . . . . . Generic equations of an integral-type non-local damage model. . . . . . Generic equations of a gradient-type non-local damage model. . . . . . 3.1 3.2 Damage model based on non-local displacements, gradient version. . . . 22 Square plate under mode I loading conditions: geometric and material parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 SENB reference test: material parameters for concrete beam (modified von Mises model with exponential damage evolution) and steel loading plates (elastic model). . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 3.3 4.1 4.2 9 9 9 Matrices belonging to the consistent tangent matrix. . . . . . . . . . . 49 Uniaxial tension test with a non-local damage model and a softening behaviour of the cohesive crack: geometric and material parameters. . . 53 xi List of Symbols Latin symbols a A b B B c C D Dcrit D DHΓd H I1 J2 k ` M MHΓd n Ni N r t t̄ t̄ d t tn ts Vector of standard nodal displacement degrees of freedom Parameter which controls the residual strength in a damage model Vector of step enriched nodal displacement degrees of freedom Parameter which controls the slope of the softening branch at the peak in a damage model Derivative shape function matrix Vector of tip enriched nodal displacement degrees of freedom Tensor of elastic moduli Damage parameter Critical damage value Diffusivity matrix Enriched diffusivity matrix Heaviside function First invariant of the strain tensor Second invariant of the deviatoric strain tensor Ratio of compressive strength to tensile strength in the modified von Mises model Characteristic length of a non-local damage model Mass matrix Enriched mass matrix Outward unit normal to the boundary Shape function of node i Shape function matrix Radial coordinate at the crack tip Time Traction vector Load on the discontinuity surface Unit tangent to the boundary Normal traction Shear traction xiii T u un ut u1 u2 ua u1a u 2a ug u 1g u 2g u ua u1a u2a ug u1g u2g uK Ju JuKn JuKs x Y Y0 Yf Ye Yg Tangent matrix for the discontinuity Displacement field Normal component of the displacement jump (embedded discontinuity models) Tangential component of the displacement jump (embedded discontinuity models) Standard displacement Enhanced displacement Local displacement field in the damage model based on non-local displacements Component of ua when Ω̄ is crossed by Γd Component of u a when Ω̄ is crossed by Γd Non-local displacement field in the damage model based on non-local displacements Component of u g when Ω̄ is crossed by Γd Component of u g when Ω̄ is crossed by Γd Nodal displacements Local nodal displacements Component of ua when Ω̄ is crossed by Γd Component of ua when Ω̄ is crossed by Γd Non-local nodal displacements Component of ug when Ω̄ is crossed by Γd Component of ug when Ω̄ is crossed by Γd Discrete displacement jump Crack opening Sliding of the crack faces Spatial coordinate vector Local state variable of a damage model Damage threshold Maximum admissible value for the state variable Non-local state variable of a damage model Non-local state variable of a damage model (via non-local displacements) Greek symbols α Γ Γd Weighting function of an integral-type non-local model Boundary surface Discontinuity surface xiv Γt Γu δΓ d ε εg εi θ ν σ ψ Ω Boundary with prescribed tractions Boundary with prescribed displacements Dirac-delta distribution centred at the discontinuity Γd Small strain tensor Small strain tensor (via non-local displacements) Principal strains Angular coordinate at the crack tip Poisson’s coefficient Cauchy stress tensor Generic enrichment function (X-FEM) Domain Operators : Double contraction ∇ Nabla operator ∇2 Laplace operator ∇s Symmetrised gradient xv Chapter 1 Introduction 1.1 Motivation Failure of quasi-brittle materials is a process characterised by formation of microcracks, strain localisation and the accumulation of damage, thus leading to the possible development of macrocracks. As a consequence, when modelling failure phenomena, all these features must be taken into account: the numerical strategy should consider the inception and the propagation of damage, the possible evolution of microcracks into macrocracks and the correct macrocrack-microcrack interaction. To simulate numerically a failure process, two different kinds of approaches have usually been employed: (a) damage mechanics, which belongs to the family of continuous models and (b) fracture mechanics, which belongs to the discontinuous models. On the one hand, by means of damage mechanics analyses, the first stages of failure of quasi-brittle materials may be described. These models are characterised by a strain softening phenomenon, which does not correctly reflect the energy dissipated in the fracture process zone. Therefore, if stress-strain laws with softening are used, numerical simulations present a pathological mesh sensitivity thus leading to physically unrealistic results. To solve the pathological mesh dependence, a regularisation technique may be used to incorporate non-locality into the model, either by an integral-type model or a gradient-type approach. However, despite the regularisation, 1 2 Introduction non-local continuum damage models cannot be used in the final stage of failure, when the body is physically separated in two or more parts. Since in these models the body is treated as a continuum body, numerical interaction between the separated parts of the body persists and unrealistic results may be obtained. On the other hand, fracture mechanics analyses, based on the cohesive zone concept, are able to deal with discontinuities. Hence, they can be employed in order to capture the last stages of failure without formation of spurious damage growth. From a numerical viewpoint, their applications were first restricted, since the standard finite element method requires that cracks must propagate along element boundaries. Nevertheless, different methods such as the eXtended Finite Element Method (X-FEM) have emerged in order to overcome this limitation and nowadays discontinuous models can adequately be used in the final stages of failure. However, discontinuous models are not able to describe neither damage inception nor its diffuse propagation. As suggested by the above discussion, in order to achieve a better characterisation of the whole failure process, a new kind of model which combine these two traditional approaches have recently appeared. The basic idea of these continuous-discontinuous strategies is to employ damage mechanics in order to describe the inception and the propagation of damage and fracture mechanics in order to deal with cracks and material separation. In this proposal, a new continuous-discontinuous approach is presented. A regularised continuum model based on non-local displacements is coupled to a discontinuous model when the damage parameter exceeds a threshold set a priori. Then, a crack described by a cohesive law is introduced and propagated through the continuous bulk according to the direction dictated by the continuum. 1.2 Layout of the proposal This proposal is organised as follows. Chapter 2 exposes the present state of the art in failure modelling by means of finite element techniques: Section 2.1 focuses on the continuum failure models, Section 1.2 Layout of the proposal 3 2.2 details the discrete approaches and finally, Section 2.3 describes some continuousdiscontinuous techniques already presented in the literature. Chapter 3 presents the candidate’s work on the regularised approach in order to achieve a realistic description of the first stages of failure phenomena. It is structured in the following sections: in Section 3.1 the gradient version of the damage model based on non-local displacements is briefly reviewed, Section 3.2 deals with the definition of the boundary conditions for the regularisation equation and some numerical examples to illustrate the regularisation capabilities are presented in Section 3.3. In Chapter 4, the coupling between the continuous and the discontinuous approach is explained. In Section 4.1, the introduction of discontinuities in the implicit gradient-enhanced continuum model based on non-local displacements is presented. Special emphasis is placed on some issues pertinent to the implementation of the combined strategy in Section 4.2. The regularisation capabilities of this continuousdiscontinuous approach are illustrated in Section 4.3 by means of two numerical examples. Finally, in Chapter 5, the future work to be developed is described and a tentative calendar is proposed and in Chapter 6, the list of congress participations is detailed. Chapter 2 State of the art In the present state of the art in finite element techniques, two different approaches to model failure phenomena are considered. On the one hand, continuum strategies can be used, where the fracture is conceived as the result of a process of strain localisation and damage accumulation. Therefore, there is not any real discontinuity in the material. On the other hand, discrete approaches may be employed, where discontinuities are introduced into the model. In this chapter, these two kinds of techniques are reviewed. First, in Section 2.1, the continuum failure models and the need for its regularisation are considered. Damage models are explained in detail in Section 2.1.1. In Section 2.2, an overview of discrete approaches is given. On the one hand, in Section 2.2.1, some general comments on traction-separation laws are made. On the other hand, in Section 2.2.2, the main discretisation methods are discussed. To finish with, some continuous-discontinuous techniques are presented in Section 2.3. 2.1 Continuum failure models In quasi-brittle materials subjected to loading conditions, the stress-strain curve is nearly linear up to the peak stress, whereas it immediately decreases after it. This phenomenon, which is known as strain softening, leads to a physically unrealistic 5 6 State of the art treatment of the energy dissipated during the failure process. Regarding numerical simulations, if stress-strain laws with softening are used, the results present a pathological mesh sensitivity: as the finite element mesh employed in the simulations is refined, the energy dissipated in the fracture process tends to zero (Jirásek, 2007a). Different solutions have been proposed in the literature to remedy this physically unrealistic behaviour (Jirásek, 2007b): • By means of the cohesive crack model, (Hillerborg et al., 1976), which admits jumps in the displacement field, softening is described by a traction-separation law. Hence, tractions transmitted by the crack are related to the displacement jump (Oliver et al., 2002). • In the crack band model, (Bažant and Oh, 1983), the process zone is represented by a band of highly localised strain. Since in numerical computations the width of this band is controlled by the size of finite elements, the softening modulus is defined according to the finite element size (Cervera and Chiumenti, 2006). • Regularised models, which consist of introducing a non-local effect, incorporate a material characteristic length that prevents strain localisation into a line thus leading to zero energy dissipation (Comi, 2001). Examples of these strategies include non-local integral or gradient-enriched formulations. On the one hand, in integral-type models, a non-local state variable is defined as the weighted average of the local state variable in a neighbourhood of the point under consideration (Bažant and Jirásek, 2002). On the other hand, in gradient-type models, higherorder derivatives are added to the partial differential equation that describes the evolution of the non-local variable (de Borst et al., 1995). In this proposal, we focus on this technique. 2.1.1 Continuum damage models Continuous damage models may be employed to describe the evolution of failure processes, between the undamaged state and macroscopic crack initiation (Lemaitre 2.1 Continuum failure models 7 and Chaboche, 1990). A generic local damage model (Table 2.1) is characterised by the following equations: • Constitutive equation x, t) = (1 − D (x x, t)) C : ε (x x, t) σ (x (2.1) where σ is the Cauchy stress tensor, ε the small strain tensor, C the tensor of elastic moduli, D the damage parameter, which ranges between 0 (undamaged material) and 1 (completely damaged material) and (:) denotes the double contraction. • Strains x, t) = ∇su (x x, t) ε (x (2.2) where ∇s is the symmetrised gradient and u stands for the displacement field. • Local state variable It is assumed that the local state variable Y depends on the strains. x, t) = Y (εε (x x, t)) Y (x (2.3) Y should account for those features of the strain field which are responsible for damage inception and propagation. Moreover, Y should be more sensitive to positive than to negative strains. In the Mazars model (Mazars, 1986), for example, Y = s X [max (0, εi )]2 (2.4) i where εi are the principal strains. On the other hand, in the modified von Mises model (de Vree et al., 1995), k−1 1 Y = I1 + 2k (1 − 2ν) 2k s k−1 I1 1 − 2ν 2 + 12k J2 (1 + ν)2 (2.5) 8 State of the art where k is the ratio of compressive strength to tensile strength, ν is the Poisson’s coefficient, I1 is the first invariant of the strain tensor and J2 is the second invariant of the deviatoric strain tensor. • Damage evolution It is assumed that the damage parameter D depends on the state variable Y . x, t) = D (Y (x x, t)) D (x (2.6) In damage models, D starts above a threshold Y0 (D = 0 for Y ≤ Y0 ) and cannot decrease (Ḋ ≥ 0). The most common expressions are the following: – Exponential law Y0 (1 − A) − Ae−B(Y −Y0 ) Y (2.7) 1 1 + B (Y − Y0 ) + A (Y − Y0 )2 (2.8) D =1− – Polynomial law D =1− where the parameters A and B control the residual strength and the slope of the softening branch at the peak respectively. – Linear softening branch Yf D= Yf − Y0 Y0 1− Y (2.9) where Yf is the maximum admissible value for the state variable. In the literature, various articles that deal particularly with damage models and the different ways to fix their spurious mesh sensitivity, either via integral-type (PijaudierCabot and Bažant, 1987) or gradient-type models (Peerlings et al., 1998), can be found. In standard regularised damage models, integral-type (Table 2.2) or gradient- 2.1 Continuum failure models 9 Table 2.1: Generic equations of a local damage model. Constitutive equation Strains Local state variable Damage evolution x, t) = (1 − D (x x, t)) C : ε (x x, t) σ (x x, t) = ∇su (x x, t) ε (x x, t) = Y (εε (x x, t)) Y (x x, t) = D (Y (x x, t)) D (x (2.10a) (2.10b) (2.10c) (2.10d) type (Table 2.3), the state variable Y incorporates the non-local effect via a characteristic length `. Table 2.2: Generic equations of an integral-type non-local damage model. Constitutive equation Strains Local state variable Non-local state variable Damage evolution x, t) = (1 − D (x x, t)) C : ε (x x, t) (2.11a) σ (x s x, t) = ∇ u (x x, t) ε (x (2.11b) x, t) = Y (εε (x x, t)) Y (x (2.11c) R α (d) Y dV x, t) = RV Ye (x (2.11d) α (d) dV V x, t) = D(Ye ) D (x (2.11e) Table 2.3: Generic equations of a gradient-type non-local damage model. Constitutive equation Strains Local state variable Non-local state variable Damage evolution x, t) = (1 − D (x x, t)) C : ε (x x, t) (2.12a) σ (x s x, t) = ∇ u (x x, t) ε (x (2.12b) x, t) = Y (εε (x x, t)) Y (x (2.12c) 2 2e e x, t) − ` ∇ Y (x x, t) = Y (x x, t) (2.12d) Y (x x, t) = D(Ye ) D (x (2.12e) 10 State of the art On the one hand, in Eq. (2.11d) the non-locality is introduced by means of a weighting function α, which depends on the distance d to the point under consideration and contains the characteristic length ` as a parameter. On the other hand, in Eq. (2.12d), Ye is the solution of a partial differential equation where Y is the source term. As shown in Jirásek (1998), apart from the state variable Y , different variables can be employed to add non-locality into the model. In this work, we propose to use a gradient non-local model based on non-local displacements (Rodrı́guez-Ferran et al., 2005) to regularise softening. 2.2 Discontinuous failure models In materials subjected to very extreme loading conditions, the localisation of deformation provokes that some macroscopical discontinuities arise. These discontinuities may be modelled as jumps in the displacement field and are named strong discontinuities, see Figure 2.1. (a) (b) (c) Figure 2.1: Kinematic description with (a) strong discontinuity; (b) weak discontinuity and (c) no discontinuities. 2.2 Discontinuous failure models 2.2.1 11 Cohesive crack models In contrast to continuum models, with smeared cracks, discontinuous models incorporate discontinuous displacement fields, thus leading to the necessity of dealing with formation and growth of cracks. In order to characterise these propagating discontinuities, different techniques, mainly based on the cohesive crack concept (Hillerborg et al., 1976), have been developed. In these approaches, the fracture is seen as a gradual phenomenon: separation occurs across an extended crack tip or a cohesive zone, see Figure 2.2. Figure 2.2: Cohesive crack process zone. To model this behaviour, a special type of constitutive law describing the crack is used. Therefore, two different kinds of constitutive laws are employed: (a) the usual stress-strain law describing the bulk material, which is still continuous and (b) a traction-separation law characterising the crack. In Figure 2.3, three different kinds of cohesive laws for one-dimensional problems are shown. (a) (b) (c) Figure 2.3: Different cohesive laws used in the literature: (a) linear with secant unloading (b) bilinear and (c) exponential laws. 12 State of the art This traction-separation law, whose definition depends on the mode of fracture (Figure 2.4), relates the tractions t̄ = [tn , ts ] transmitted by the crack to the disuK = [JuKn , JuKs ], where JuKn is the crack opening and JuKs is the placement jump Ju relative sliding of the crack faces. (a) (b) (c) Figure 2.4: The three fracture modes: (a) Mode I or opening mode (b) Mode II or sliding mode and (c) Mode III or tearing mode. 2.2.2 Computational modelling of strong discontinuities The Finite Element Method (FEM), which performs well approximating smooth functions, is not suited for the approximation of non-smooth solutions. Hence, special techniques (Jirásek and Belytschko, 2002) have to be used to incorporate displacement discontinuities in numerical models. Here, these methods are briefly described. Remeshing In remeshing methods (Bouchard et al., 2000, 2003; Patzák and Jirásek, 2004), the standard FEM is used. Nevertheless, an appropriate mesh must be built: in these methods, element faces (or element edges in two dimensions) have to be aligned with the crack and its nodes are doubled and distributed to both sides of the discontinuity, see Figure 2.5. One advantage of this method is its easy implementation, since only a mesher and a standard finite element program are needed. Nevertheless, remeshing as the crack 2.2 Discontinuous failure models 13 Figure 2.5: The mesh conforms to crack geometry. grows presents certain limitations: • Remeshing requires projection of variables between the different meshes and causes some difficulties during post-processing. • Mesh refinement is required where the solution is expected to have singularities, thus leading to an expensive technique from the computational viewpoint. • In some problems dealing with non-linear crack propagation or the growth of intersecting cracks, having an adequate mesh is very difficult or even impossible. Due to these disadvantages, other methods allowing cracks with arbitrary trajectory have been developed. Embedded discontinuities In embedded discontinuity models (see Jirásek (2000) for classification), a discrete crack is modelled through the inclusion of strong discontinuities embedded in finite elements. In this formulation, the cracks are not necessarily aligned with the element boundaries but they are able to grow across the continuum elements. In embedded discontinuity models, the displacement field can be decomposed into a continuous and a discontinuous part. The crack is then represented by additional degrees of freedom referring to the normal un and tangential ut component of the displacement jump, see Figure 2.6(b). 14 State of the art (a) (b) Figure 2.6: Triangular element crossed by a crack (embedded discontinuity model). Elements with embedded discontinuities provide better approximation solutions than pure continuum models, which smear displacement jumps. On the other hand, compared to remeshing techniques, here the entire crack may be represented independently of the finite element mesh. Moreover, since the additional degrees of freedom un and ut have an internal character, no extra global degrees of freedom are introduced and the global equilibrium equations may be written only in terms of the nodal displacements. However, as discussed in Jirásek and Belytschko (2002), elements with embedded discontinuities still present some limitations. By means of this formulation, it is possible to reproduce an arbitrary jump at a certain point, but in the split element, strains on both sides of the crack remain the same since the strain in the bulk material is still interpolated in a continuous way. Due to this disadvantage, it is preferable to use the eXtended Finite Element Method (X-FEM), which is able to reproduce exactly the separation and the independent deformation of the split parts. Extended finite element method One of the latest improvements in modelling crack growth are the methods based on the partition of unity concept (Melenk and Babuška, 1996; Babuška and Melenk, 1998), among which the eXtended Finite Element Method (X-FEM) is the most employed. Detailed overviews of the developments of X-FEM have been given by Karihaloo and Xiao (2003); Abdelaziz and Hamouine (2008); Yazid et al. (2009); Belytschko et al. (2009). Here, the basic features of crack growing by means of X-FEM 2.2 Discontinuous failure models 15 are briefly reviewed. Main features of X-FEM In X-FEM (Belytschko and Black, 1999; Moës et al., 1999), displacements are approximated by the sum of two continuous displacement fields, one of which is multiplied by a discontinuous function in order to model the discontinuities. Thus, the continuous part corresponds to the displacement field without any crack, while the discontinuous or the enriched contribution (the partition of unity enrichment) takes into account the discontinuities. Hence, the displacement field u can be decomposed as x) = u 1 (x x) + ψ(x x)u u2 (x x) u (x (2.13) where u 1 and u 2 , which are continuous fields, are the regular and enhanced displacex) is the enrichment function, which is discontinuous ment fields respectively and ψ(x across the domain. Therefore, the basic idea of X-FEM is to add discontinuous enrichment functions to the finite element approximation in order to include information from asymptotic solutions and other knowledge of the properties of the solution. The enrichment function is then chosen depending on the kind of information which is incorporated into the solution. For the particular case of crack modelling, X-FEM should take into account two kinds of aspects: (a) the discontinuity field along the crack faces and (b) the crack tip singularity. Enrichment functions Consider a finite element mesh of a cracked body, as seen in Figure 2.7. Let I denote the set of all nodes in the finite element mesh, J the set of nodes of elements around the crack tip (called tip enriched nodes and indicated by circles in Figure 2.7) and K the set of nodes of elements crossed by the crack but not in J (called step enriched nodes and indicated by squares in Figure 2.7). Then, the X-FEM displacement approximation for a crack is ! x) = u(x X i∈I x)ai + Ni (x X j∈J x)H(x x)bj + Nj (x X k∈K x) Nk (x X l x)clk ψ l (x (2.14) 16 State of the art Figure 2.7: A crack line (dashed line) in a structured mesh with standard elements (white), elements whose nodes are all enriched (dark grey) and blending elements (light grey). Nodes in J and K are indicated by circles and squares respectively. Adapted from Moës et al. (1999). x) is the Heaviside step function where Ni are the standard FEM shape functions, H(x x) is a which allows to represent the displacement jump along the crack faces, ψ l (x set of enrichment functions which approximates the crack tip behaviour, ai are the standard nodal degrees of freedom, bi are the step enriched nodal degrees of freedom and ci are the tip enriched nodal degrees of freedom. To approximate the crack tip behaviour, Belytschko and Black (1999); Stolarska et al. (2001) use for the two-dimensional problem the functions √ θ θ θ θ ψ (r, θ) = r sin , cos , sin sin θ, cos sin θ 2 2 2 2 l (2.15) where r and θ are polar coordinates with origin at the crack tip and parallel to the crack faces, see Figure 2.8. To approximate the displacement jump along the crack faces, different step functions have been used in the literature, such as the Heaviside (Simone et al., 2003; Wells et al., 2002; Wells and Sluys, 2001) or the sign function (Moës and Belytschko, 2002; Zi and Belytschko, 2003; Comi and Mariani, 2007; Bechet et al., 2005; Mariani and Perego, 2003). 2.2 Discontinuous failure models 17 Figure 2.8: Polar coordinates used to evaluate the tip enrichment functions. It should be stressed that different authors (see for example Comi et al. (2007); Simone et al. (2003)) assume that the crack tip always belongs to an element edge thus avoiding the use of tip enrichment functions. Then, the X-FEM displacement approximation for a crack is simply x) = u(x X i∈I x)ai + Ni (x X x)H(x x)bj Nj (x (2.16) j∈J Note that X-FEM enrichment involves extra degrees of freedom for the nodes in the domain subjected to the enrichment. Nevertheless, in Eq. (2.14) and (2.16), the enrichment is added only where it is needed thus leading to a computationally efficient method since in general few extra unknowns are added. Due to this local enrichment, three different kinds of elements exist: (a) standard elements with no enriched nodes, (b) elements whose nodes are all enriched and (c) elements with some of their nodes enriched, see Figure 2.7. These hybrid elements are commonly named blending elements and involve problems in the solution accuracy as reported in Fries (2008); Chessa et al. (2003); Gracie et al. (2008). Numerical integration When integrating X-FEM functions, two different difficulties arise: both the discontinuous functions along the crack faces and the singularities at the crack tip must be taken into account. Since the traditional quadrature rules, for example Gauss quadratures, are designed to integrate polynomials and functions that are well approximated by polynomials, these quadratures are not valid to inte- 18 State of the art grate X-FEM functions properly. In order to do that, several different approaches have been used in the literature, see Belytschko et al. (2009). The usual method is to employ subdomain quadratures, see Belytschko and Black (1999); Moës et al. (1999), in which the element is subdivided into quadrature subdomains, whose boundaries are aligned with the crack, see Figure 2.9. For elements cut by the crack and enriched with the step function, this strategy solves the problem, since the functions are continuous in each subdomain and standard quadratures may be employed. Nevertheless, for elements containing the crack tip, there still exists a singularity in the displacement field. In standard FEM, two different techniques may be used to solve problems dealing with singularities: (a) increasing the number of integration points, which does not perform well with X-FEM, see Zlotnik (2008), and (b) using special remeshing techniques that we want to avoid. In order to solve this problem, special methods, consisting also of subdivisions, have been proposed in Laborde et al. (2005) and Bechet et al. (2005). Figure 2.9: Subdomain quadrature: the elements cut by the crack are subdivided into subdomains (dashed lines). 2.3 Continuous-discontinuous failure models Continuous-discontinuous models emerged to achieve a better characterisation of the whole failure process. The basic idea of these integrated strategies is to combine continuous and discontinuous models. The former obtain realistic results in the first stages of failure process, while are not able to reproduce cracks and material separa- 2.3 Continuous-discontinuous failure models 19 tion. On the other hand, discontinuous models can describe the propagating cracks but not the initial states of fracture (Mazars and Pijaudier-Cabot, 1996). The main features of these combined strategies are summarised here: • Non-local continuous models are used to describe the first stages of failure. Thus, numerical simulations do not present mesh sensitivity and physically realistic results are obtained. • At the end of each time step, the approach checks if the transition criterion is fulfilled. In such a case, a discrete cohesive crack is introduced into the model and the direction of its propagation is determined. • From that moment on, a discontinuous approach is used to model the final stages of the failure process. Therefore, the numerical interaction between the separated parts of the body ceases and realistic results may be obtained. Different integrated strategies have been already proposed in the literature, some of which are briefly reviewed here. Jirásek and Zimmermann (2001) analyse the combination of the smeared and embedded descriptions of cracking. The authors propose to use a model dealing with inelastic strain in order to characterise the early stages of material degradation and displacement discontinuities to deal with the highly localised fracture. In Wells et al. (2002), a numerical model that allows traction-free discontinuities in a softening viscoplastic bulk is presented. Here, the transition takes place when a critical threshold of inelastic deformation is reached. From that moment on, when the plastic deformation in the continuum around a discontinuity tip reaches a critical level, the discontinuous surface is extended. In Simone et al. (2003), an implicit gradient-enhanced continuum damage model is used to describe the first steps of the fracture process. Nevertheless, when the damage parameter is close to one, a traction-free crack is introduced and a discontinuous interpolation of the problem fields is employed thus preventing from spurious growth of damage. 20 State of the art In Comi et al. (2007), the early steps of failure process are also modelled by means of a non-local continuum damage approach. When the damage parameter exceeds a critical value, which is defined a priori, this is combined to an extended finite element cohesive crack model in order to describe the final stages of failure. The transition from the continuous to the discontinuous approach is based on an energy balance, that is the fracture energy not yet dissipated in the damage band is transferred to the cohesive zone, while the bulk unloads. In this work, a new contribution in this direction is presented. A non-local continuum damage model based on non-local displacements is used for the continuum. When the damage parameter exceeds a threshold set a priori Dcrit , a crack described by a cohesive law relating traction to displacement jump is introduced. We propose to determine the crack path by means of the continuum: the gradient of the damage field is employed. Once the crack is introduced, the growing crack is modelled by means of the X-FEM. In this model, the transition from a continuum to a discontinuous model is defined as follows: damage value is fixed to Dcrit and the bulk material unloads. Chapter 3 Continuous model of failure based on non-local displacements Regularised damage formulations provide an objective description of the first stages of a failure process, when the bulk is considered to be continuous. They are based on non-local fields which incorporate non-locality into the model. In this work, a formulation with regularised displacements is employed in order to obtain physically realistic results. The idea of a damage model with non-local displacements was presented and illustrated by means of one-dimensional examples by Rodrı́guez-Ferran et al. (2005). In this work, we extend the applicability of this alternative formulation to a twodimensional setting. First, we propose new boundary conditions which allow to regularise two-dimensional boundary problems. In addition, several examples are presented in order to validate the approach in a two-dimensional setting. The structure of the chapter is as follows. In Section 3.1 the gradient version of the damage model based on non-local displacements is briefly reviewed. Special emphasis is placed on the definition of the boundary conditions for the regularisation equation in Section 3.2. The regularisation capabilities are illustrated by means of some numerical examples in Section 3.3. Finally, the concluding remarks in Section 3.4 close this chapter. 21 22 Continuous model of failure based on non-local displacements 3.1 Gradient continuous non-local damage model In the implicit gradient-enhanced continuum model based on non-local displacements, two different displacements are used to formulate the model: (a) the standard or local displacements u a and (b) the gradient-enriched displacement field u g , which is the solution of a partial differential equation with u a being the source term. This regularisation PDE is the diffusion-reaction equation ug (x x, t) − `2 ∇2ug (x x, t) = ua (x x, t) (3.1) where ` is a parameter added in the diffusion term with the dimension of length. The model is summarised in Table 3.1. Table 3.1: Damage model based on non-local displacements, gradient version. Constitutive equation Local strains Non-local displacements Non-local strains Non-local sate variable Damage evolution σ (x x, t) = (1 − D (x x, t)) C : ε (x x, t) x, t) = ∇su a (x x, t) ε (x 2 2 x, t) − ` ∇ u g (x x, t) = u a (x x, t) u g (x s x, t) = ∇ u g (x x, t) ε g (x x, t) = Y (εεg (x x, t)) Yg (x x, t) = D(Yg ) D (x (3.2a) (3.2b) (3.2c) (3.2d) (3.2e) (3.2f) As Table 3.1 reflects, in this proposal, u g is an auxiliary regularised displacement field that drives the damage evolution. 3.2 Boundary conditions for the regularisation equation Integral-type formulations that fix spurious mesh sensitivity present some important drawbacks, particularly when dealing with non-locality in the neighbourhood of the 3.2 Boundary conditions for the regularisation equation 23 boundary (Peerlings et al., 1996). As an alternative to these non-local descriptions, gradient-enriched formulations have been used in the literature. The advantage of using a gradient-enriched description is that although they are non-local models, they are local from a mathematical viewpoint, since non-local interaction is accounted for by means of higher-order derivatives. Nevertheless, the main disadvantage of gradient approaches arises from the requirement of additional boundary conditions: in order to solve the regularisation equation, boundary conditions have to be prescribed, which is still an open issue in these formulations. In standard gradient non-local damage models, homogeneous Neumann boundary conditions ∇Ye · n = 0 on ∂Ω (3.3) (where n denotes the outward unit normal to Ω and Ye the non-local state variable) are typically prescribed, due to the difficulty of motivating Dirichlet boundary conditions, that is prescribing Ye . In the damage model based on non-local displacements, the boundary conditions seem to be easier to interpret. In this approach, a natural option is to prescribe Dirichlet boundary conditions (Rodrı́guez-Ferran et al., 2005): ug = ua on ∂Ω (3.4) These boundary conditions have a clear physical interpretation: local and nonlocal displacements coincide along all the domain boundary (that is, for both the Dirichlet and Neumann boundaries of the mechanical problem). However, as discussed in Jirásek and Marfia (2006), this may have the negative effect of not allowing displacement smoothing along the boundary, since u g and u a are imposed to be equal on ∂Ω. Such effect, especially negative in problems where localisation starts in the boundary, may lead to spurious narrowing of the damage zone, as shown in Jirásek and Marfia (2006), Rodrı́guez-Ferran et al. (2009) and Tamayo-Mas and Rodrı́guez-Ferran (2010). 24 Continuous model of failure based on non-local displacements In order to solve this problem, non-homogeneous Neumann boundary conditions were suggested by Jirásek and Marfia (2006): ug · n = ∇u ua · n ∇u on ∂Ω (3.5) (where n is the outward unit normal to the boundary). Note that by means of boundary conditions (3.5), displacement smoothing along the boundary is accepted. Nevertheless, boundary conditions (3.5) do not ensure volume conservation. Indeed, assuming a constant density and using the Gauss’ theorem, volume preservation means Z Z ug − u a ) dΩ = ∇ · (u 0= Ω ug − u a ) · n dΓ (u (3.6) ∂Ω which is satisfied if Eq. (3.4) is employed but it is not fulfilled in general with boundary conditions (3.5). As an alternative to Eq. (3.4) and Eq. (3.5), combined boundary conditions are proposed here: Dirichlet boundary conditions are prescribed for the normal component of the displacement field whereas Neumann boundary conditions are imposed for the tangential one. Both homogeneous, Eq. (3.7), and non-homogeneous Neumann boundary conditions, Eq. (3.8), are considered: ug · n = ua · n ug · t ) · n = ∇ (u ug · n = ) on ∂Ω (3.7) 0 ua · n ug · t ) · n = ∇ (u ua · t ) · n ∇ (u ) on ∂Ω (3.8) where n and t are the directions normal and tangent to the boundary ∂Ω respectively. By means of essential boundary conditions (3.7)1 and (3.8)1 , volume preservation is ensured. In addition, either homogeneous or non-homogeneous Neumann boundary conditions allow displacement smoothing along the boundary: Eq. (3.7)2 allows a free 3.2 Boundary conditions for the regularisation equation 25 relative slip while the relative slips of local and non-local displacements are prescribed to coincide if condition (3.8)2 is employed, which is a more restrictive condition. Note that combined boundary conditions coincide with Dirichlet boundary conditions (3.4) in a one-dimensonal setting. Interestingly, if the local field u a is linear, the boundary value problem consisting of the differential equation (3.1) and boundary conditions (3.4), (3.5) or (3.8) admits solution u g = u a . Nevertheless, this is not the solution of Eq. (3.1) if combined equations with homogeneous Neumann boundary condition for the tangential component are considered. Therefore, by means of Eq. (3.7), the modification of local displacement fields into non-local ones does alter linear fields and since reproducibility of order 1 is not ensured, spurious damage caused by small rigid rotations may occur. In order to illustrate the above discussion, the regularisation equation x) − `2 ∇2 ug (x x) = ua (x x) ug (x (3.9) defined on the unit square [0, 1] × [0, 1] and three different scalar source terms ua are considered. As a first test, ua is assumed to be linear, see Figure 3.1(a). The boundary value problem consisting of the differential equation (3.9) with the four proposed boundary conditions is solved. As seen in Figure 3.1, given a linear function ua , solutions x) = ua (x x) are admitted if Dirichlet, Neumann or combined with non-homogeneous ug (x Neumann boundary conditions are employed, thus guaranteeing reproducibility of x) = ua (x x) is not the solution of Eq. (3.9) if boundary order 1. Nevertheless, ug (x conditions (3.7) are prescribed on the boundary, see Figure 3.1(d). As observed, in order to fulfill the imposed boundary conditions, a high gradient solution is obtained near the corners of the domain, which may lead to spurious damage caused by small rigid rotations. As a second test, ua is considered to be the function shown in Figure 3.2(a). Again, the problem is solved using the four proposed boundary conditions. As shown in Figure 3.2(b), Dirichlet boundary conditions do not allow displacement smoothing along the boundary. By means of Neumann or combined boundary conditions, this is 26 Continuous model of failure based on non-local displacements 10 10 5 5 0 1 0 1 1 0.5 1 0.5 0.5 0.5 0 0 0 0 (a) (b) 10 10 10 5 5 5 0 1 0 1 0 1 1 1 0.5 0.5 0.5 0.5 1 0.5 0.5 0 0 0 0 0 0 (c) (d) (e) x) = ua (x, y) = 1 + Figure 3.1: Validation test with (a) a linear source term ua (x x + 5y. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. permitted, see Figures 3.2(c), 3.2(d) and 3.2(e). As a third test, the source term shown in Figure 3.3(a) is analysed. Again, Dirichlet boundary conditions (3.4) do not allow a relative slip along the boundary, see Figure 3.3(b). However, this is permitted if Neumann or combined boundary conditions are employed. As seen in 3.3(d), by means of homogeneous Neumann boundary conditions, a free relative slip is allowed and no oscillations along the boundary appear. 3.3 Numerical examples: validation of the model 1 1 0.5 0.5 0 1 1 27 0 1 0.5 1 0.5 0.5 0.5 0 0 0 0 (a) (b) 1 1 1 0.5 0.5 0.5 0 0 0 1 1 1 1 0.5 0.5 1 0.5 0.5 1 0.5 0.5 0 0 0 0 0 0 (c) (d) (e) Figure 3.2: Validation test with (a) a tent function source term. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. 3.3 Numerical examples: validation of the model The goal of this section is to illustrate the regularisation capabilities of the damage model based on non-local displacements with combined boundary conditions (3.7). Two different examples are carried out. In Section 3.3.1, a square plate under mode I loading conditions is analysed and in Section 3.3.2, a single-edge notched beam test is considered. 28 Continuous model of failure based on non-local displacements 1 1 0.5 0.5 0 1 0 1 1 1 0.5 0.5 0.5 0.5 0 0 0 0 (a) (b) 1 1 1 0.5 0.5 0.5 0 1 0 1 0 1 1 0.5 0.5 1 1 0.5 0.5 0.5 0.5 0 0 0 0 0 0 (c) (d) (e) Figure 3.3: Validation test with (a) a tent function source term. Solutions obtained by means of (b) Dirichlet, (c) Neumann, (d) Combined (homogeneous Neumann) and (e) Combined (non-homogeneous Neumann) boundary conditions. 3.3.1 Square plate under mode I loading conditions The first example concerns the simulation of a pure mode I problem. It deals with the solution of a square plate in tension subjected to a prescribed displacement at the top and bottom side and clamped at the right one, see Figure 3.4. In order to cause localisation, a weakened region whose size depends on the finite element discretisation is considered. The test is carried out according to a simplified Mazars criterion, see Equation (2.4), and a linear softening law, see Equation (2.9). The dimensionless geometric and material parameters for this test are summarised in Table 3.2. 3.3 Numerical examples: validation of the model 29 Figure 3.4: Square plate under mode I loading conditions: problem statement. Table 3.2: Square plate under mode I loading conditions: geometric and material parameters. Meaning Length of the specimen Length of weaker part Width of weaker part Young’s modulus Idem of weaker part Poisson’s coefficient Damage threshold Final strain Characteristic length Symbol L LW hW E EW ν Y0 Yf ` Value 10 1 1 finite element 20 000 18 000 (10% reduction in E) 0 10−4 −2 1.25 √ × 10 7 × 10−4 The regularisation properties of the model are assessed by carrying out the analysis with four different meshes of 10 × 11, 20 × 21, 30 × 31 and 40 × 41 elements, see Figure 3.5. The damage profiles with the deformed meshes and the force-displacement curves 30 Continuous model of failure based on non-local displacements (a) Mesh 1: 10 × 11 elements. (b) Mesh 2: 20 × 21 elements. (c) Mesh 3: 30 × 31 elements. (d) Mesh 4: 40 × 41 elements. Figure 3.5: Square plate under mode I loading conditions. Four meshes with different element density and different imperfection sizes are used. are shown in Figure 3.6 and 3.7 respectively. As seen, the force-displacement curve and the width of damage band do not depend on numerical parameters such as the finite element mesh or the imperfection size needed to cause localisation. 3.3.2 Single-edge notched beam As a second example, a single-edge notched beam (SENB) subjected to an antisymmetrical four-point loading is considered. The geometry, loads and supports, shown in Figure 3.8, correspond to the test carried out by (Rodrı́guez-Ferran and Huerta, 2000). A plane stress analysis is performed. The test is carried out with the modified von Mises model Eq. (2.5) with exponential damage evolution Eq. (2.7) and the material parameters of Table 3.3. As a first test, a fixed characteristic length ` = √ 10 mm is chosen. The analysis is 3.3 Numerical examples: validation of the model (a) Mesh 1: 10 × 11 elements. (b) Mesh 2: 20 × 21 elements. (c) Mesh 3: 30 × 31 elements. (d) Mesh 4: 40 × 41 elements. 31 Figure 3.6: Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: damage profiles with deformed meshes (×100). carried out with four different meshes, see Figure 3.9. The final damage profiles and the force-displacement curves are shown in Figure 3.10 and 3.11 respectively. As expected, regularisation via non-local displacements with combined boundary conditions Eq. (3.7) solves the pathological mesh dependence. As a second test, a fixed characteristic length ` = 10 mm is chosen. The numerical analysis is carried out again with the four meshes shown in Figure 3.9. The forcedisplacement curves and the final damage profiles are shown in Figure 3.12 and 3.13 respectively. As seen, neither the force-displacement curve nor the width of damage profiles depend on numerical parameters such as the finite element size. Moreover, as 32 Continuous model of failure based on non-local displacements 18 10x11 mesh 20x21 mesh 30x31 mesh 40x41 mesh 16 14 Force 12 10 8 6 4 2 0 0 0.02 0.04 0.06 0.08 Displacement 0.1 Figure 3.7: Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: force-displacement curves. Figure 3.8: Single-edge notched beam: problem statement. All distances in mm. expected, the characteristic length ` controls the ductility of the material. Nevertheless, as shown in Figure 3.13, some spurious damage appears at the boundary. In fact, two different phenomena are observed. On the one hand, some spurious damage emerges due to the punctual loads. Since in this second test the characteristic length of the non-local technique is greater than in the first test, more diffusion is introduced into the model and the width of this spurious damage is in- 3.4 Concluding remarks 33 Table 3.3: SENB reference test: material parameters for concrete beam (modified von Mises model with exponential damage evolution) and steel loading plates (elastic model). Meaning Young’s modulus Poisson’s coefficient Compressive-to-tensile strength ratio Damage threshold Residual strength Slope of the soft. branch at peak Symbol E ν k Y0 A B Concrete 28 000 MPa 0.1 10 1.5 × 10−4 0.8 9 000 Steel 280 000 MPa 0.2 10 creased. On the other hand, some physically unrealistic damage is observed at the lower right-hand corner of the specimen. Although in this part of the specimen the beam behaves as a rigid body and no deformation is observed, non-local strains are nonzero thus leading to positive values of the non-local state variable, Eq. (3.2e), that are able to damage the specimen, Eq. (3.2f). In order to solve this pathological behaviour, which is due to the boundary conditions for the regularisation equation, the same test with combined equations and non-homogeneous Neumann boundary conditions for the tangential component is going to be studied. 3.4 Concluding remarks The main results of the present chapter can be summarised as follows: • A gradient-enriched continuous formulation is employed in order to describe the evolution of failure processes, between the undamaged state and macroscopic crack initiation. In this approach, two different displacement fields are used: (a) the standard or local displacements u a and (b) the gradient-enriched displacement field u g , which drives the damage evolution. This non-local displacement field is defined as the solution of a diffusion differential equation. 34 Continuous model of failure based on non-local displacements Hence, additional boundary conditions should be prescribed. • Dirichlet boundary conditions have a clear physical meaning: the two displacement fields are imposed to coincide along all the domain boundary. Nevertheless, in a multi-dimensional setting, this leads to spurious narrowing of the damage zone at the boundary, where displacement smoothing is not permitted. • Although non-homogeneous Neumann boundary conditions allow this displacement smoothing, they are not expected to regularise the problem neither, since volume conservation is not ensured. • In order to solve the regularisation equation, combined boundary conditions can be used. By means of these conditions, local and non-local displacements coincide along the normal direction to the boundary thus ensuring volume conservation. Moreover, some displacement along the tangent direction to the boundary is allowed. • Two different types of combined boundary conditions may be prescribed: either homogeneous or non-homogeneous Neumann boundary condition can be imposed for the tangential component. By means of the homogeneous Neumann boundary condition, a free relative slip is permitted. However, if a nonhomogeneous Neumann boundary condition is prescribed, the relative slips of local and non-local displacements coincide. • If the local displacement field is linear, the regularisation equation with Dirichlet, Neumann and combined boundary conditions with non-homogeneous Neumann does admit solution u g = u a , thus guaranteeing reproducibility of order 1. Such requirement is not ensured if combined equations with homogeneous Neumann bounary condition are employed. So, the transformation of local displacement fields into non-local ones modify linear fields. • A pure mode I problem is carried out to exhibit the regularisation capabilities of this strategy by means of combined boundary conditions with homogeneous 3.4 Concluding remarks 35 Neumann. As expected, the numerical results do not suffer from pathological mesh sensitivity and physically realistic force-displacement diagrams and damage profiles are obtained. • A mixed-mode problem is also analysed using two different characteristic lengths. The results are quite successful if little diffusion is added into the model. However, at later stages of the process, spurious damage growth appears when a greater characteristic length is employed. Such effect is caused by the boundary conditions for the regularisation equation. In order to avoid them, combined equations with non-homogeneous Neumann will be analysed in our further research. 36 Continuous model of failure based on non-local displacements (a) Mesh 1: 407 elements, 465 nodes. (b) Mesh 2: 763 elements, 841 nodes. (c) Mesh3: 2997 elements, 3154 nodes. (d) Mesh 4: 4244 elements, 4436 nodes. Figure 3.9: SENB reference test. Four meshes with different element density are used. 3.4 Concluding remarks 37 (a) Mesh 1. (b) Mesh 2. (c) Mesh 3. (d) Mesh 4. Figure 3.10: SENB reference test. Fixed characteristic length ` = various meshes: final damage profiles. √ 10 mm with 38 Continuous model of failure based on non-local displacements 60 Mesh 1 Mesh2 Mesh3 Mesh4 50 Force (kN) 40 30 20 10 0 0 0.02 0.04 CMSD (mm) 0.06 0.08 Figure 3.11: SENB reference test. Fixed characteristic length ` = various meshes: force-displacement curves. 70 Mesh 1 Mesh2 Mesh3 Mesh4 60 50 Force (kN) √ 10 mm with 40 30 20 10 0 0 0.05 CMSD (mm) 0.1 Figure 3.12: SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: force-displacement curves. 3.4 Concluding remarks 39 (a) Mesh 1. (b) Mesh 2. (c) Mesh 3. (d) Mesh 4. Figure 3.13: SENB reference test. Fixed characteristic length ` = 10 mm with various meshes: final damage profiles. Chapter 4 Continuous-discontinuous model based on non-local displacements As already seen, by means of a non-local continuum approach, the damage inception and its propagation can be simulated properly and physically realistic results are obtained. Nevertheless, for increasing levels of damage, a continuum non-local model is not able to simulate the physical discontinuities that can arise. For increasing loads, this may cause an unrealistic spread of damage (Comi et al., 2007). In order to solve this bad performance of continuum non-local techniques, a new model is presented here: once the damage parameter exceeds a threshold set a priori, we propose to couple the implicit gradient-enhanced damage continuum model with a discontinuous approach allowing local displacements u a to admit discontinuities. In addition, and for consistency purposes, see the regularisation equation (3.1), non-local displacements are also modelled as discontinuous fields. The structure of the chapter is as follows. In Section 4.1, the introduction of discontinuities in the implicit gradient-enhanced continuum model based on non-local displacements is presented. First, the definition of the discontinuous problem fields is carried out in Section 4.1.1. Then, the governing equations are described in Section 4.1.2 and the variational formulation is derived in Section 4.1.3. Finally, the finite element discretisation is presented in Section 4.1.4. Special emphasis is placed on 41 42 Continuous-discontinuous model based on non-local displacements some finite element issues such as the crack-introduction or the crack-orientation criteria in Section 4.2. The regularisation capabilities of this continuous-discontinuous approach are illustrated in Section 4.3 by means of two numerical examples. Finally, the concluding remarks in Section 4.4 close this chapter. 4.1 Gradient continuous-discontinuous non-local damage model 4.1.1 Problem fields Consider the continuum body Ω bounded by Γ. The boundary Γ is composed of Γu , Γt and Γd such that Γ = Γu ∪Γt ∪Γd , as shown in Figure 4.1. Prescribed displacements are imposed on Γu , while prescribed tractions are imposed on Γt . The boundary Γd consists of the boundary of the crack. Figure 4.1: Notations for a body with a crack subjected to loads and imposed displacements. Then, in the body Ω̄, by means of the X-FEM, the standard displacement field ua can be decomposed as x) + HΓd (x x) u 2a (x x) x) = u 1a (x u a (x (4.1) x) (i = 1, 2) are continuous fields and HΓd is the Heaviside function centred where u ia (x 4.1 Gradient continuous-discontinuous non-local damage model 43 at the discontinuity Γd . In this work, the sign function ( x) = HΓd (x 1 if x ∈ Ω̄+ −1 if x ∈ Ω̄− (4.2) (also called modified or generalised Heaviside function) centred at the discontinuity surface Γd is employed, because of its symmetry (Zi and Belytschko, 2003). A similar decomposition holds for the gradient-enriched displacements u g x) = u 1g (x x) + HΓd (x x) u 2g (x x) u g (x (4.3) x) (i = 1, 2) are continuous fields and HΓd is the Heaviside function defined where u ig (x in Eq. (4.2). Therefore, in the gradient-enhanced continuous-discontinuous model based on nonlocal displacements, two different displacements are used to formulate the model: (a) the standard displacements u a and (b) the gradient-enriched displacements u g . By means of the X-FEM, both fields are approximated by the sum of a continuous and a discontinuous displacement field. The continuous part corresponds to the displacement field without any crack, while is the discontinuous or the enriched displacement field the additional displacement that models the discontinuities. 4.1.2 Governing equations The equilibrium equations and boundary conditions for the body Ω̄ without body forces can be summarised as ∇·σ = 0 in Ω (4.4a) σ · n = t̄ on Γt (4.4b) σ · m = t̄ d on Γd (4.4c) u a = u ∗a on Γu (4.4d) 44 Continuous-discontinuous model based on non-local displacements where σ is the Cauchy stress tensor, n is the outward unit normal to the body, m is the inward unit normal to Ω+ on Γd , u∗a is a prescribed displacement, t̄ is the load on the boundary and t̄ d is the load on the discontinuity surface. Note that equation (4.4c) represents traction continuity at the discontinuity surface Γd . The strong form of the mechanical problem is completed by the damage constitutive relation σ (x x, t) = [1 − D (x x, t)] C : ε (x x, t) (4.5) In the regularisation approach employed in this work, the second-order diffusion partial differential equation x, t) − `2 ∇2u g (x x, t) = u a (x x, t) u g (x in Ω \ Γd (4.6) is coupled with the mechanical equations, also in a discontinuous setting. Both for the standard and the enhanced displacement fields, boundary conditions must be prescribed. Similarly as done in Section 3.2, different kinds of boundary conditions may be imposed. On the one hand, Dirichlet u ig = u ia on ∂Ω ∪ Γd (4.7) or Neumann boundary conditions uig · n = ∇u uia · n ∇u on ∂Ω ∪ Γd (4.8) where i = 1, 2, can be employed. As an alternative, combined boundary conditions are proposed here. Again, as suggested in Section 3.2, both homogeneous and non-homogeneous Neumann boundary conditions are considered for the tangential component of the displacement field: u ig ·n = ∇ u ig · t · n = u ia ·n 0 on ∂Ω u ig ·m = ∇ u ig · t · m = u ia ·m 0 on Γd (4.9) 4.1 Gradient continuous-discontinuous non-local damage model 45 = u ia · n u ig · n on ∂Ω uia · t ) · n ∇ u ig · t · n = ∇ (u (4.10) u ig · m = u ia · m on Γd i i u t m u t m ∇ g· · = ∇ (u a · ) · where i = 1, 2. 4.1.3 Variational formulation In this section, the variational formulation is derived: both the governing equations (4.4) and the regularisation equation (4.6) with boundary conditions 4.9 are cast in a weak form. The space of trial local displacements is defined by the function x, t) = u 1a (x x, t) + HΓd (x x)u u2a (x x, t) , u a (x u 1a , u 2a ∈ Uu , (4.11) where Uu = 1 2 u a , u a | u 1a , u 2a ∈ H 1 (Ω) and u a |Γu = u ∗a (4.12) with H 1 (Ω) a Sobolev space. The equilibrium equation (4.4a) is multiplied by the weight function ω (x x, t) = ω 1 (x x, t) + HΓd (x x)ω ω 2 (x x, t) , ω 1 , ω 2 ∈ Wu ,0 (4.13) with Wu ,0 = 1 2 ω , ω | ω 1 , ω 2 ∈ H 1 (Ω) and ω 1|Γu = ω 2|Γu = 0 , (4.14) and integrated over the domain Ω to obtain the weak equilibrium statement. After 46 Continuous-discontinuous model based on non-local displacements standard manipulations, the following expressions are obtained: Z s 1 Z ω 1 · t̄ dΓ Γt ZΩ Z Z s 2 2 HΓd ∇ ω : σ dΩ + 2 ω · t̄ d dΓ = HΓd ω 2 · t̄t dΓ ω 1 ∈ H 1 (Ω) (4.15a) ∀ω ∇ ω : σ dΩ = Ω Γd ω 2 ∈ H 1 (Ω) (4.15b) ∀ω Γt where at the discontinuity, ua K t̄t˙ d = TJu̇ (4.16) ua K. with T relating traction rate t̄t˙ d and displacement jump rate Ju̇ Similarly to local displacements, the space of trial non-local displacements u g is defined by the function x, t) = u 1g (x x, t) + HΓd (x x)u u2g (x x, t) , u g (x u 1g , u 2g ∈ Uu , (4.17) where Uu is defined in Eq. (4.12). Eq. (4.6) can be cast in a variational form by multiplication with the vector x, t) Eq. (4.13) and integration over the domain Ω. After standard test function ω (x manipulations, one obtains Z 1 u 1g HΓd u 2g 2 Z 1 u1g ∇u u2g HΓd ∇u 2 Z ω : u2gm dΓ ω · + dΩ + ` ∇ω + dΩ − ` HΓd ω 1 · ∇u Ω Ω Γd Z Z ω 1 ∈ Wu ,00 −2`2 ω 1 ∇ δΓd m · u 2g dΩ = ω 1 · u 1g + HΓd u 2g dΩ ∀ω (4.18a) Ω Ω Z Z Z 2 2 2 2 1 2 1 2 ug dΩ − ` u1gm dΓ ω : HΓd ∇u ug + ∇u HΓd ω 2 · ∇u ω · HΓd u g + u g dΩ + ` ∇ω Ω Ω Z Z Γd u1g − HΓd ∇u u2g − HΓd ∇ δΓd m · u 2g dΩ = +2`2 ω 2 · δΓd m ∇u ω 2 · HΓd u 1a + u 2a dΩ Ω Ω ω 2 ∈ Wu ,00 ∀ω where δΓd is the Dirac delta centred at the discontinuity surface Γd . (4.18b) 4.1 Gradient continuous-discontinuous non-local damage model 4.1.4 47 Discretised and linearised weak governing equations In FE analysis, using a Galerkin discretisation, Eq. (4.1) and (4.3) read, for nodes whose support is crossed by Γd , x) = N(x x)u1a + HΓd (x x)N(x x)u2a ua (x (4.19a) x) = N(x x)u1g + HΓd (x x)N(x x)u2g ug (x (4.19b) where N is the matrix of standard finite element shape functions, u1a/g are the basic nodal degrees of freedom and u2a/g are the enhanced ones. The discrete format of the problem fields leads to the four discrete weak governing equations fint,u1a = fext,u1a (4.20a) fint,u2a = fext,u2a (4.20b) (M + `2 D)u1g + (MHΓd + `2 DHΓd )u2g = Mu1a + MHΓd u2a (4.20c) (MHΓd + `2 DHΓd )u1g + (M + `2 D)u2g = MHΓd u1a + Mu2a (4.20d) where Z fint,u1a = ZΩ fext,u1a = BT σ dΩ (4.21a) NT t̄ dΓ (4.21b) Γt Z T Z HΓd B σ dΩ + 2 fint,u2a = Ω Z fext,u2a = NT t̄ d dΓ (4.21c) Γd HΓd NT t̄ dΓ (4.21d) NT N dΩ (4.21e) ∇NT ∇N dΩ (4.21f) HΓd NT N dΩ (4.21g) HΓd ∇NT ∇N dΩ (4.21h) Γt Z M = ZΩ D = ZΩ MHΓd = DHΓd = ZΩ Ω 48 Continuous-discontinuous model based on non-local displacements with B the matrix of shape function derivatives. Some remarks about the discretisation: • Eq. (4.20a) is the standard non-linear system of equilibrium equations, while Eq. (4.20b) takes into account the contribution of the crack. • In Eq. (4.21c), the contribution of the crack is multiplied by a factor of two due to the chosen definition of the Heaviside function, see Eq. (4.2). • Matrices M and D are the mass and diffusivity matrices already obtained in (Rodrı́guez-Ferran et al., 2005). They are both constant. • Matrices MHΓd and DHΓd can be understood as enriched mass and diffusivity matrices respectively, since the expression is the same as M and D except for the Heaviside function. • Note that the property HΓd HΓd = +1, which is derived from the definition of the Heaviside function Eq. (4.2), is used. In summary, the finite element discretisation results in requil,u1a := fint,u1a − fext,u1a = 0 (4.22a) requil,u2a := fint,u2a − fext,u2a = 0 (4.22b) rregu,u1g := (M + `2 D)u1g + (MHΓd + `2 DHΓd )u2g − Mu1a − MHΓd u2a = 0 (4.22c) rregu,u2g := (MHΓd + `2 DHΓd )u1g + (M + `2 D)u2g − MHΓd u1a − Mu2a = 0 (4.22d) where fint,u1a , fext,u1a , fint,u2a , fext,u2a are defined in Eq. (4.21a - 4.21d). The consistent tangent matrix is K 1 1 ua ,ua K 2 1 ua ,ua Ku1 ,u1 g a Ku2g ,u1a Ku1a ,u2a Ku1a ,u1g Ku1a ,u2g Ku2a ,u2a Ku2a ,u1g Ku2a ,u2g Ku1g ,u2a Ku1g ,u1g Ku1g ,u2g Ku2g ,u2a Ku2g ,u1g Ku2g ,u2g (4.23) 4.1 Gradient continuous-discontinuous non-local damage model 49 with the matrices defined in Table 4.1, so the linearised weak form at iteration i within a time step k reads k,i−1 k,i−1 k,i−1 Kk,i−1 u1a ,u1a Ku1a ,u2a Ku1a ,u1g Ku1a ,u2g k,i−1 k,i−1 k,i−1 K 2 1 Kk,i−1 ua ,ua u2a ,u2a Ku2a ,u1g Ku2a ,u2g k,i−1 Ku1 ,u1 Kk,i−1 1 1 u1g ,u2a Kug ,ug Ku1g ,u2g g a k,i−1 2 1 2 2 Kk,i−1 u2g ,u1a Ku2g ,u2a Kug ,ug Kug ,ug δu1a k,i δu2 k,i a δu1g k,i δu2g k,i −rk,i−1 equil,u1a −rk,i−1 equil,u2a = 0 0 (4.24) Table 4.1: Matrices belonging to the consistent tangent matrix. Ku1a ,u1a := R Ω Ku1a ,u1g := − Ku2a ,u1a := R R Ω Ku2a ,u1g := − BT CB dΩ g BT CεεD0 (Yg ) ∂Y B dΩ ∂εεg Ω HΓd BCB dΩ R Ω g B dΩ HΓd BT CεεD0 (Yg ) ∂Y ∂εεg Ku1a ,u2a := R Ω Ku1a ,u2g := − Ku1a ,u2a := R Ω R Ω Ku2a ,u2g := − HΓd BT CB dΩ g B dΩ HΓd BT CεεD0 (Yg ) ∂Y ∂εεg BT CB dΩ + 2 R Ω R Γd NT TN dΓ g B dΩ BT CεεD0 (Yg ) ∂Y ∂εεg Ku1g ,u1a := −M Ku1g ,u2a := −MHΓd Ku1g ,u1g := M + `2 D Ku1g ,u2g := MHΓd + `2 DHΓd Ku2g ,u1a := −MHΓd Ku2g ,u2a := −M Ku2g ,u1g := MHΓd + `2 DHΓd Ku2g ,u2g := M + `2 D Note that the arrays N and B multiplying u1a , u2a , u1g and u2g are not the same since only part of the degrees of freedom in the arrays u1g and u2g are activated. Some remarks about the tangent matrix (4.23): • Matrix Ku1a ,u1a is the secant tangent matrix already obtained in (Rodrı́guezFerran et al., 2005). Matrices Ku1a ,u2a and Ku2a ,u1a may be understood as enriched secant tangent matrices, since the expression is the same, except for the Heaviside function. 50 Continuous-discontinuous model based on non-local displacements • Matrices Ku1a ,u1g and Ku2a ,u2g are the local tangent matrices already obtained in (Rodrı́guez-Ferran et al., 2005). As done before, matrices Ku1a ,u2g and Ku2a ,u1g can be understood as enriched local tangent matrices. • Although the mass and diffusivity matrices are constant, the enriched ones may increase during the numerical simulation, since the crack is allowed to propagate through the bulk. Nevertheless, MHΓd and DHΓd are considered to be constant during a fixed time step. • Thanks to the linear relation between the degrees of freedom u1a , u2a , u1g and u2g , rregu,u1g and rregu,u2g are zero. • Note again that, during the manipulations in Table 4.1, the property HΓd HΓd = +1 is used. 4.2 Finite element technology 4.2.1 Introducing a discontinuity In combined strategies, the transition between the continuous and the discontinuous approach takes place when a critical situation is achieved, whose definition depends on the underlying continuous model. In a damaging continuum approach, for example, we will say that a critical situation is achieved when the damage parameter at one integration point exceeds a critical damage value set a priori. Therefore, as soon D > Dcrit , a crack described by a cohesive law is initiated, damage value is fixed to Dcrit and the bulk material unloads, see Figure 4.2. In order to preserve the robustness of the Newton-Raphson method, this crack is introduced as a straight segment at the end of a time step. This procedure is repeated in the elements ahead of the crack tip until the crack-introduction criterion is no longer satisfied. To model a crack tip, the displacement jump at the discontinuity tip is set to zero. In order to prevent crack opening and sliding at the current crack tip, only 4.2 Finite element technology (a) 51 (b) Figure 4.2: Constitutive law for the cracked bulk: (a) elastic unloading with D = Dcrit ; (b) linear traction-separation law for the crack. standard degrees of freedom for the nodes of the edge containing the crack tip are considered, see Figure 4.3. As soon the discontinuity is extended in the next element, nodes behind the crack tip are enriched. Figure 4.3: Sketch of the cohesive tip region. A crack line (dashed line) in a mesh with standard elements (white) and elements whose nodes are enriched (grey). Enriched nodes with H = +1 and H = −1 are indicated by squares and circles respectively. 4.2.2 Orienting a discontinuity In a regularised continuous model, the crack growth direction cannot be analytically derived, (Simone et al., 2003). In this work, we propose that the crack propagates according to the steepest descent direction of the damage profile, see Figure 4.4. 52 Continuous-discontinuous model based on non-local displacements Figure 4.4: Determination of the propagation direction: the crack propagates according to the direction perpendicular to the isolines of the damage field. 4.3 Numerical examples: validation of the model The regularisation capabilities of this new strategy are illustrated in this section by means of two numerical examples. In Section 4.3.1, a uniaxial tension test is carried out using a two-dimensional geometry, and in Section 4.3.2 the two-dimensional square plate under mode I loading conditions analysed in Section 3.3.1 is retrieved. 4.3.1 2D uniaxial tension test This first example, Tamayo-Mas and Rodrı́guez-Ferran (2009), deals with the solution of a bar in tension subjected to imposed displacement at the free side and clamped at the other one, see Figure 4.5. Since in the first steps of the failure process a continuum damage model is used, the central tenth of the bar is weakened to cause localisation. A non-local continuum damage model is employed in the first stages of the failure process, according to a simplified Mazars criterion Eq. (2.4) and a linear softening law Eq. (2.9), see Figure 4.6(a). When the damage parameter exceeds a threshold set a priori called Dcrit , a discontinuity is introduced and the continuous-discontinuous technique is used. In order to characterise the crack, a linear traction-separation law with secant unloading is considered, see Figure 4.6(b). 4.3 Numerical examples: validation of the model 53 Figure 4.5: Uniaxial tension test: problem statement. (a) (b) Figure 4.6: Evolution law for (a) the bar; (b) the crack. The dimensionless geometric and material parameters for this test are summarised in Table 4.2. Table 4.2: Uniaxial tension test with a non-local damage model and a softening behaviour of the cohesive crack: geometric and material parameters. Meaning Length of the bar Width of the bar Length of weaker part Young’s modulus Idem of weaker part Damage threshold Final strain Critical damage Crack stiffness Symbol L A LW E EW Y0 Yf Dcrit T Value 100 1 L/7 20 000 18 000 10−4 1.25 × 10−2 0.9 −20 54 Continuous-discontinuous model based on non-local displacements The regularisation properties of the model are analysed by means of different tests. √ As a first test, a fixed characteristic length ` = 5 is chosen. The analysis is carried out with six different meshes. The force-displacement curves and the damage profiles are shown in Figure 4.7. As desired, the responses for this test do not depend on finite element sizes. 651 Elem. 357 Elem. 105 Elem. 63 Elem. 21 Elem. 7 Elem. Force 1.5 1 0.5 0 0 1 651 Elem. 357 Elem. 105 Elem. 63 Elem. 21 Elem. 7 Elem. 0.8 Damage 2 0.6 0.4 0.2 0.02 0.04 0.06 Displacement 0.08 0.1 0 0 20 (a) 40 X 60 80 100 (b) Figure 4.7: Uniaxial tension test. Fixed characteristic length ` = meshes. (a) force-displacement curve; (b) damage profiles. √ 5 with various As a second test, a fixed mesh of 105 elements is considered and four different √ √ √ √ characteristic lengths are used, ` = 1, 2, 5, 10. The results are depicted in Figure 4.8. The ductility in the force-displacement response and the width of the final damage profile increase with the internal length scale. Finally, as a third test, a fixed mesh of 105 elements and a fixed characteristic √ length ` = 5 are chosen. Two different tests, in which the size of weakened region differs, are analysed. Results are shown in Figure 4.9. As seen, there is no pathological dependence on imperfection size. In summary, this new model exhibits the desired regularisation capabilities. 4.3.2 Square plate under mode I loading conditions As a second example, the square plate shown in Figure 3.4 is retrieved. In order to simulate the first steps of the failure process, the particular damage model presented 4.3 Numerical examples: validation of the model 2 1 0.5 0 0 2 l =10 l2=5 l2=2 l2=1 0.8 Damage Force 1 2 l =10 l2=5 l2=2 l2=1 1.5 55 0.6 0.4 0.2 0.02 0.04 0.06 Displacement 0.08 0 0 0.1 20 (a) 40 X 60 80 100 (b) Figure 4.8: Uniaxial tension test. Fixed mesh with various characteristic lengths. (a) force-displacement curve; (b) damage profiles. 1 LW=L/7 LW=L/21 Damage 0.8 0.6 0.4 0.2 0 0 (a) 20 40 X 60 80 100 (b) Figure 4.9: Uniaxial tension test. Fixed mesh and characteristic length with various imperfection sizes. (a) force-displacement curve; (b) damage profiles. in Section 3.3.1 is considered, see Table 3.2. When the damage parameter exceeds the threshold Dcrit , which is set to 0.95, a growing crack is introduced and the combined strategy is employed. To characterise the crack, a linear traction-separation law with secant unloading is considered. In this particular test, the normal crack stiffness is set to T = −208.33. The regularisation properties of the model are assessed by carrying out the analysis with three different meshes, see Figures 3.5(b)-3.5(d). The damage profiles with the 56 Continuous-discontinuous model based on non-local displacements deformed meshes and the force-displacement curves are shown in Figure 4.10 and 4.11 respectively. As seen, the force-displacement curve and the width of damage band do not depend on numerical parameters such as the finite element mesh or the imperfection size needed to cause localisation. (a) Mesh 2: 20 × 21 elements. (b) Mesh 3: 30 × 31 elements. (c) Mesh 4: 40 × 41 elements. Figure 4.10: Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: damage profiles with deformed meshes (×100). As shown in Figure 4.10, there exist some uncracked regions with D > Dcrit . In order to fissure them, two main issues must be first taken into account. On the one hand, the ability to deal with multiple non-intersecting cracks should be admitted into our finite element code. On the other hand, crack branching phenomenon should be modelled and also introduced into our finite element program. 4.4 Concluding remarks 57 Force 15 10 5 0 0 20x21 Mesh 30x31 Mesh 40x41 Mesh 2 4 Displacement 6 −3 x 10 Figure 4.11: Square plate under mode I loading conditions. Fixed characteristic length with various meshes and imperfection sizes: force-displacement curves. In addition, in Figure 4.11, some oscillations in the force-displacement diagrams are observed. This behaviour is due to the use of X-FEM with Heaviside enrichment only, which gives a binary description of the crack tip element (cracked or not cracked), (Menouillard and Belytschko, 2010). Different methods have been developed in order to avoid these spurious waves thus additional research is required to couple them with the proposed combined strategy. 4.4 Concluding remarks The main results of the present chapter can be summarised as follows: • A gradient-enriched continuous formulation is enhanced with a discontinuous interpolation of the problem fields in order to describe the final stages of failure processes, where macroscopic cracks arise. In this continuous-discontinuous technique, both standard displacements u a and gradient-enhanced displacement field u g may admit discontinuities. • The eXtended Finite Element Method (X-FEM) is used to incorporate dis- 58 Continuous-discontinuous model based on non-local displacements placement discontinuities in the numerical model thus requiring extra degrees of freedom. In this proposal, the crack tip is assumed to belong to an element edge and only the Heaviside function is employed in order to describe crack propagation. • The main features of this new combined strategy are summarised here: – A continuous non-local damage model based on non-local displacements is used to describe the first stages of failure. Therefore, numerical results that do not present mesh sensitivity are obtained. – At the end of each time step, the strategy checks if the transition criterion is fulfilled. In this proposal, the transition between the continuous and the discontinuous approach takes place when the damage parameter exceeds a critical value set a priori. Hence, if D > Dcrit , a crack described by a cohesive law is introduced. By now, only linear laws with secant unloadings are considered. – Once the crack is introduced, the discontinuous setting coexists with the continuous one. In fact, here the continuum is used for crack path tracking: the crack propagates according to the direction dictated by the gradient of the damage field. • In order to implement this discontinuous strategy, four different matrices are needed: the standard M and the enhanced MHΓd mass matrices and the standard D and the enhanced DHΓd diffusivity matrices. The standard M and D matrices, already obtained in (Rodrı́guez-Ferran et al., 2005), are constant. However, the enhanced matrices may change during the numerical simulation, since the crack propagates through the continuous bulk. • Two different examples have been implemented to validate the strategy. On the one hand, a one-dimensional problem is carried out. The expected regularisation capabilities of the continuous-discontinuous model are obtained. On the other hand, a two-dimensional problem under mode I loading conditions is studied. 4.4 Concluding remarks 59 By means of this example, it may be seen that the proposed combined approach does regularise softening. Nevertheless, some further research is required in order to extend its applicability to problems involving crack branching. Apart from that, some spurious oscillations are observed in the force-displacement curves due to the use of X-FEM with step enrichment only, which should be avoided. Chapter 5 Future work The final objective of this thesis is the computational analysis of a whole failure process. Hence, to achieve this goal, different steps have been considered, which are shown in the tentative schedule presented in Figure 5.1. Moreover, each of the future work topics are detailed in the following list. Figure 5.1: Work schedule. • Boundary conditions for the regularisation equation As explained in Section 3.2, prescribing appropriate boundary conditions for the regularisation equation is still an open issue in these formulations. In this proposal, four different boundary conditions are analysed: (a) Dirichlet boundary conditions, which do not allow displacement smoothing along the boundary; 61 62 Future work (b) non-homogeneous Neumann boundary conditions, which do not ensure volume preservation and (c) two different kinds of combined boundary conditions, which allow some displacement along the tangent direction to the boundary and ensure volume conservation. On the one hand, homogeneous Neumann boundary conditions for the tangential component have been employed, which allow a free relative slip but lack the ability to ensure reproducibility of order 1. On the other hand, by means of non-homogeneous Neumann boundary conditions for the tangential component, the relative slips of local and non-local displacements are prescribed to coincide. Although this is a more restrictive condition, reproducibility of order 1 is guaranteed, thus preventing from spurious damage caused by small rigid rotations. As suggested by the above discussion, further research in this direction is needed. On the one hand, these four boundary conditions are being analysed by means of the single-edge notched beam. On the other hand, new numerical tests such as the Nooru-Mohamed test (Nooru-Mohamed, 1992) will be carried out in order to validate the model. • Multiple non-intersecting discontinuities By now, problems involving one single crack propagating through the continuous bulk are analysed. Additional research is required in order to deal with n nonintersecting discontinuities. Indeed, if a body Ω̄ is crossed by n non-intersecting cracks, both the standard u a and the enhanced u g displacement fields can be decomposed as x) = u 0a (x x) + u a (x x) = u 0g (x x) + u g (x n X x) u ia (x x) Hi (x i=1 n X x) u ig (x x) Hi (x (5.1a) (5.1b) i=1 where u ia and u ig , ∀ i = 0÷n, are continuous functions on Ω̄ and Hi are Heaviside 63 functions centred at the discontinuity surface Γi : ( x) = Hi (x 1 if x ∈ Ω̄+ i (5.2) −1 if x ∈ Ω̄− i Hence, more complicated problems such as a four-point bending test with n notches will be carried out. • Crack branching The example presented in 4.3.2 is not completely simulated. The main reason is that the proposed strategy lacks the ability to involve crack branching. Two main issues arise when dealing with crack branching. On the one hand, different strategies to model the branched element can be considered. In (Linder and Armero, 2009), three of them are studied, see Figure 5.2. (a) Element deletion. (b) Element with a single discontinuity. (c) Element with embedded branching. Figure 5.2: Representation of the branching. Although crack branching may not occur at an angle of 90◦ , the approximation shown in Figure 5.2(c) is the most convenient one and it will be adopted in our further research. On the other hand, the finite element implementation should be studied in detail. The eXtended Finite Element Method (X-FEM) has been successfully used in problems involving non-intersecting cracks. However, in the case of branched and intersecting discontinuities, modelling them as independent is not suitable and a hierarchy between them should be considered, (Daux et al., 2000; Zlotnik and Dı́ez, 2009). Different numerical techniques have been 64 Future work developed in order to deal with crack branching, which will be investigated in the near future. • Application to other models By now, only damage models to simulate failure of quasi-brittle materials have been used. The idea is to extend the applicability of the proposed formulation to a more generalised setting. On the one hand, plasticity models are going to be studied. On the other hand, ductile damage and failure modelling will be analysed. Chapter 6 Publications (1) Tamayo-Mas, E. and A. Rodrı́guez-Ferran, Continuous-discontinuous models of failure based on non-local displacements, Congreso de Métodos Numéricos en Ingenierı́a 2009, Barcelona (Spain). June 29-July 2, 2009. (2) Rodrı́guez-Ferran, A., E. Tamayo-Mas, T. Bennett and H. Askes, A ContinuousDiscontinuous Model for Softening and Cracking based on Non-Local Gradient Elasticity, Complas X - X International Conference on Computational Plasticity Fundamentals and Applications, Barcelona (Spain). September 2-4, 2009. (3) Tamayo-Mas, E. and A. Rodrı́guez-Ferran, A continuous-discontinuous model for softening and cracking based on non-local displacements, ECCM 2010 - IV European Conference on Computational Mechanics, Paris (France). May 16-21, 2010. 65 Bibliography Abdelaziz, Y. and A. Hamouine (2008). A survey of the extended finite element. Computers and Structures 86 (11-12), 1141–1151. Babuška, I. and J. M. Melenk (1998). The partition of unity method. International Journal for Numerical Methods in Engineering 40 (4), 727–758. Bažant, Z. P. and M. Jirásek (2002). Nonlocal integral formulations of plasticity and damage: survey of progress. Journal of Engineering Mechanics 128 (11), 1119–1149. Bažant, Z. P. and B. H. Oh (1983). Crack band theory for fracture of concrete. Materials and Structures 16 (3), 155–177. Bechet, E., H. Minnebo, N. Moës, and B. Burgardt (2005). Improved implementation and robustness study of the X-FEM for stress analysis around cracks. International Journal for Numerical Methods in Engineering 64 (8), 1033–1056. Belytschko, T. and T. Black (1999). Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering 45 (5), 601–620. Belytschko, T., R. Gracie, and G. Ventura (2009). A review of extended/generalized finite element methods for material modeling. Modelling and Simulation in Materials Science and Engineering 17 (4), 043001–043024. Bouchard, P. O., F. Bay, and Y. Chastel (2003). Numerical modelling of crack propagation: automatic remeshing and comparison of different criteria. Computer Methods in Applied Mechanics and Engineering 192 (35-36), 3887–3908. Bouchard, P. O., F. Bay, Y. Chastel, and I. Tovena (2000). Crack propagation modelling using an advanced remeshing technique. Computer Methods in Applied Mechanics and Engineering 189 (3), 723–742. Cervera, M. and M. Chiumenti (2006). Smeared crack approach: back to the original track. International Journal for Numerical and Analytical Methods in Geomechanics 30 (12), 1173–1199. 67 68 Bibliography Chessa, J., H. Wang, and T. Belytschko (2003). On the construction of blending elements for local partition of unity enriched finite elements. International Journal for Numerical Methods in Engineering 57 (7), 1015–1038. Comi, C. (2001). A non-local model with tension and compression damage mechanisms. European Journal of Mechanics - A/Solids 20 (1), 1–22. Comi, C. and S. Mariani (2007). Extended finite element simulation of quasi-brittle fracture in functionally graded materials. Computer Methods in Applied Mechanics and Engineering 196 (41-44), 4013–4026. Comi, C., S. Mariani, and U. Perego (2007). An extended FE strategy for transition from continuum damage to mode I cohesive crack propagation. International Journal for Numerical and Analytical Methods in Geomechanics 31 (2), 213–238. Daux, C., N. Moës, J. Dolbow, N. Sukumar, and T. Belytschko (2000). Arbitrary branched and intersecting cracks with the extended finite element method. International Journal for Numerical Methods in Engineering 48 (12), 1741–1760. de Borst, R., J. Pamin, R. H. J. Peerlings, and L. J. Sluys (1995). On gradientenhanced damage and plasticity models for failure in quasi-brittle and frictional materials. Computational Mechanics 17 (1-2), 130–141. de Vree, J. H. P., W. A. M. Brekelmans, and M. A. J. V. Gils (1995). Comparison of nonlocal approaches in continuum damage mechanics. Computers and Structures 55 (4), 581–588. Fries, T. P. (2008). A corrected XFEM approximation without problems in blending elements. International Journal for Numerical Methods in Engineering 75 (5), 503– 532. Gracie, R., H. Wang, and T. Belytschko (2008). Blending in the extended finite element method by discontinuous Galerkin and assumed strain methods. International Journal for Numerical Methods in Engineering 74 (11), 1645–1669. Hillerborg, A., M. Modeer, and P. A. Petersson (1976). Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research 6 (6), 773–782. Jirásek, M. (1998). Nonlocal models for damage and fracture: comparison of approaches. International Journal of Solids and Structures 35 (31-32), 4133–4145. Jirásek, M. (2000). Comparative study on finite elements with embedded discontinuities. Computer Methods in Applied Mechanics and Engineering 188 (1-3), 307–330. Bibliography 69 Jirásek, M. (2007a). Mathematical analysis of strain localization. Revue Européenne de Génie Civil 11 (7-8), 977–991. Jirásek, M. (2007b). Nonlocal damage mechanics. Civil 11 (7-8), 993–1021. Revue Européenne de Génie Jirásek, M. and T. Belytschko (2002). Computation resolution of strong discontinuities. In Fifth World Congress on Computational Mechanics. Jirásek, M. and S. Marfia (2006). Nonlocal damage models: displacement-based formulations. In Meschke, de Borst, Mang, and Bičanič (Eds.), EURO-C 2006 Computational Modelling of Concrete Structures, held in Mayrhofen, Austria, London, UK, pp. 381–390. Taylor & Francis Group. Jirásek, M. and T. Zimmermann (2001). Embedded crack model: II. combination with smeared cracks. International Journal for Numerical Methods in Engineering 50 (6), 1291–1305. Karihaloo, B. L. and Q. Z. Xiao (2003). Modelling of stationary and growing cracks in FE framework without remeshing: a state-of-the-art review. Computers and Structures 81 (3), 119–129. Laborde, P., J. Pommier, Y. Renard, and M. Salaün (2005). High-order extended finite element method for cracked domains. International Journal for Numerical Methods in Engineering 64 (3), 354–381. Lemaitre, J. and J. L. Chaboche (1990). Mechanics of solid materials. Cambridge University Press. Linder, C. and F. Armero (2009). Finite elements with embedded branching. Finite Elements in Analysis & Design 45 (4), 280–293. Mariani, S. and U. Perego (2003). Extended finite element method for quasi-brittle fracture. International Journal for Numerical Methods in Engineering 58 (1), 103– 126. Mazars, J. (1986). A description of micro- and macroscale damage of concrete structures. Journal of Engineering Fracture Mechanics 25 (5-6), 729–737. Mazars, J. and G. Pijaudier-Cabot (1996). From damage to fracture mechanics and conversely: a combined approach. International Journal of Solids and Structures 33 (20-22), 3327–3342. Melenk, J. M. and I. Babuška (1996). The partition of unity finite element method: basic theory and applications. Computer methods in applied mechanics and engineering 139 (1-4), 289–314. 70 Bibliography Menouillard, T. and T. Belytschko (2010). Smoothed nodal forces for improved dynamic crack propagation modeling in XFEM. International Journal for Numerical Methods in Engineering, DOI = 10.1002/nme.2882 (early view). Moës, N. and T. Belytschko (2002). Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics 69 (7), 813–833. Moës, N., J. Dolbow, and T. Belytschko (1999). A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering 46 (1), 131–150. Nooru-Mohamed, M. B. (1992). Mixed-mode fracture of concrete: an experimental approach. Ph. D. thesis, Technische Universiteit Delft. Oliver, J., A. E. Huespe, M. D. G. Pulido, and E. Chaves (2002). From continuum mechanics to fracture mechanics: the strong discontinuity approach. Engineering Fracture Mechanics 69 (2), 113–136. Patzák, B. and M. Jirásek (2004). Adaptive resolution of localized damage in quasibrittle materials. Journal of Engineering Mechanics 130 (6), 720–732. Peerlings, R. H. J., R. de Borst, W. A. M. Brekelmans, and J. H. P. de Vree (1996). Gradient enhanced damage for quasi-brittle materials. International Journal for Numerical Methods in Engineering 39 (19), 3391–3403. Peerlings, R. H. J., R. de Borst, W. A. M. Brekelmans, and M. G. D. Geers (1998). Gradient-enhanced damage modelling of concrete fracture. Mechanics of cohesivefrictional materials 3 (4), 323–342. Pijaudier-Cabot, G. and Z. P. Bažant (1987). Nonlocal damage theory. Journal of Engineering Mechanics - ASCE 118 (10), 1512–1533. Rodrı́guez-Ferran, A. and A. Huerta (2000). Error estimation and adaptivity for nonlocal damage models. International Journal of Solids and Structures 37 (48-50), 7501–7528. Rodrı́guez-Ferran, A., I. Morata, and A. Huerta (2005). A new damage model based on non-local displacements. International Journal for Numerical and Analytical Methods in Geomechanics 29 (5), 473–493. Rodrı́guez-Ferran, A., E. Tamayo-Mas, T. Bennett, and H. Askes (2009). A continuous-discontinuous model for softening and cracking based on non-local gradient elasticity. In Complas X - X International Conference on Computational Plasticity Fundamentals and Applications - Barcelona (Spain). Bibliography 71 Simone, A., G. N. Wells, and L. J. Sluys (2003). From continuous to discontinuous failure in a gradient-enhanced continuum damage model. Computer Methods in Applied Mechanics and Engineering 192 (41-42), 4581–4607. Stolarska, M., D. L. Chopp, N. Moës, and T. Belytschko (2001). Modelling crack growth by level sets in the extended finite element method. International Journal for Numerical Methods in Engineering 51 (8), 943–960. Tamayo-Mas, E. and A. Rodrı́guez-Ferran (2009). Continuous-discontinuous models of failure based on non-local displacements. In Congreso de Métodos Numéricos en Ingenierı́a (METNUM 09) - Barcelona (Spain). Tamayo-Mas, E. and A. Rodrı́guez-Ferran (2010). A continuous-discontinuous model for softening and cracking based on non-local displacements. In ECCM 2010 - IV European Conference on Computational Mechanics, Paris (France). Wells, G. N. and L. J. Sluys (2001). A new method for modelling cohesive cracks using finite elements. International Journal for Numerical Methods in Engineering 50 (12), 2667–2682. Wells, G. N., L. J. Sluys, and R. D. Borst (2002). Simulating the propagation of displacement discontinuities in a regularized strain-softening medium. International Journal for Numerical Methods in Engineering 53 (5), 1235–1256. Yazid, A., N. Abdelkader, and H. Abdelmadjid (2009). A state-of-the-art review of the X-FEM for computational fracture mechanics. Applied Mathematical Modelling 33 (12), 4269–4282. Zi, G. and T. Belytschko (2003). New crack-tip elements for XFEM and applications to cohesive cracks. International Journal for Numerical Methods in Engineering 57 (15), 2221–2240. Zlotnik, S. (2008). Numerical modeling of transient multiphase thermo-mechanical problems: application to the oceanic lithosphere. Ph. D. thesis, Universitat de Barcelona. Zlotnik, S. and P. Dı́ez (2009). Hierarchical X-FEM for n-phase flow (n > 2). Computer Methods in Applied Mechanics and Engineering 198 (30-32), 2329–2338.