6.1. Definición de operación binaria UNIDAD VI. ESTRUCTURAS

6.1. Definición de operación binaria
Algebra universitaria
UNIDAD VI. ESTRUCTURAS ALGEBRÁICAS
6.1. Definición de operación binaria
Se conoce una operación binaria aquella que al operar dos números (de
ahí su nombre) se obtiene un tercero.
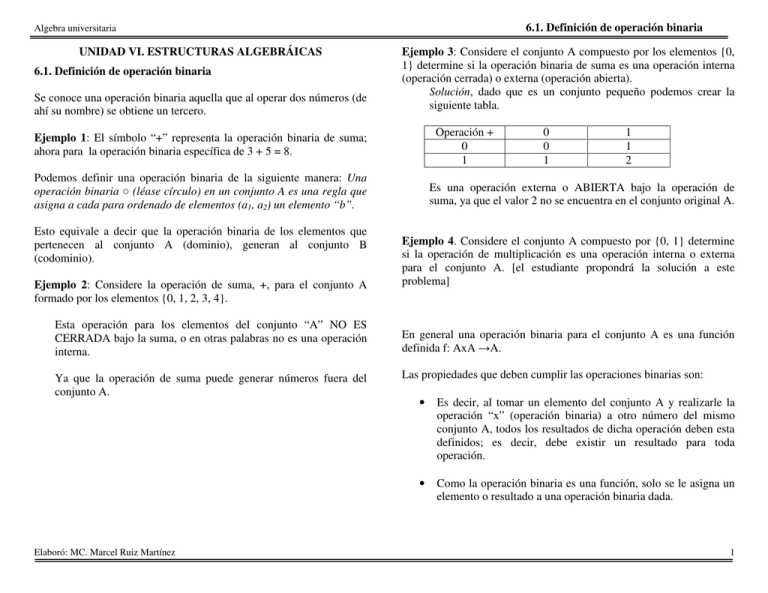
Ejemplo 3: Considere el conjunto A compuesto por los elementos {0,
1} determine si la operación binaria de suma es una operación interna
(operación cerrada) o externa (operación abierta).
Solución, dado que es un conjunto pequeño podemos crear la
siguiente tabla.
Operación +
0
1
Ejemplo 1: El símbolo “+” representa la operación binaria de suma;
ahora para la operación binaria específica de 3 + 5 = 8.
Podemos definir una operación binaria de la siguiente manera: Una
operación binaria ○ (léase círculo) en un conjunto A es una regla que
asigna a cada para ordenado de elementos (a1, a2) un elemento “b”.
Esto equivale a decir que la operación binaria de los elementos que
pertenecen al conjunto A (dominio), generan al conjunto B
(codominio).
Ejemplo 2: Considere la operación de suma, +, para el conjunto A
formado por los elementos {0, 1, 2, 3, 4}.
Esta operación para los elementos del conjunto “A” NO ES
CERRADA bajo la suma, o en otras palabras no es una operación
interna.
Ya que la operación de suma puede generar números fuera del
conjunto A.
Elaboró: MC. Marcel Ruiz Martínez
0
0
1
1
1
2
Es una operación externa o ABIERTA bajo la operación de
suma, ya que el valor 2 no se encuentra en el conjunto original A.
Ejemplo 4. Considere el conjunto A compuesto por {0, 1} determine
si la operación de multiplicación es una operación interna o externa
para el conjunto A. [el estudiante propondrá la solución a este
problema]
En general una operación binaria para el conjunto A es una función
definida f: AxA →A.
Las propiedades que deben cumplir las operaciones binarias son:
•
Es decir, al tomar un elemento del conjunto A y realizarle la
operación “x” (operación binaria) a otro número del mismo
conjunto A, todos los resultados de dicha operación deben esta
definidos; es decir, debe existir un resultado para toda
operación.
•
Como la operación binaria es una función, solo se le asigna un
elemento o resultado a una operación binaria dada.
1
Algebra universitaria
Ejemplo 5. Sea A ϵ ℝ; determinar si la operación
ón binaria de división
para el conjunto de los números reales cumple con los requisitos para
ser una operación binaria;; y en todo caso indicar si es una operaci
operación
binaria abierta o cerrada.
Solución: No cumple, dado que la división
ón de un número real “a”
entre cero no esta definida.
Ejemplo 6. Sea A ϵ ℤ; determinar si la operación
ón binaria de resta para
entre los números del conjunto A cumple con los requisitos para
considerarse una operación
ón binaria, y si fuera el caso, identificar si es
abierta o cerrada bajo dicha operación binaria.
[El estudiante propone una solución]
6.1. Definición
Definici de operación binaria
d
por las reglas de la
Ejemplo 9.. Para las operaciones binarias descritas
siguiente tabla mostrada a continuación:
continuaci
Casos: a) y b) identifique en cada caso si son conmutativas.
NOTA: Para realizar una operación
ón por ejemplo: a * c; lo primero que
debe hacerse es buscar el renglón
ón que contenga la “a” y después la
columna que contenga el valor “b””; la intersección o la parte de
adentro
ro representa el resultado de la operación,
operaci
en este caso en el
inciso a) a * c = b
Propiedad conmutativa
Una operación binaria es conmutativa si se cumple que para dos
números “a” y “b”:
a*b = b * a
(cuidado, el “*” para estos casos no es una multiplicaci
multiplicación, sino
una operación binaria cualquiera)
Ejemplo 7. Identificar si para el conjunto de los enteros ℤ la operación
binaria de suma definida como a + b es conmutativa.
Solución: si es conmutativa, dado que:
a+b=b+a
1+2=2+1
Ejemplo 8. Identificar si para el conjunto de los enteros ℤ la operación
binaria de resta definida como a - b es conmutativa.
[El estudiante propone una solución]
[El estudiante propone una solución]
Propiedad asociativa
Una operación binaria es asociativa
sociativa si cumple con la condición
siguiente:
a*(b*c) = (a*b)*c
(Recordar: el “*” para estos casos no es una multiplicación, sino
una operación
ón binaria cualquiera)
Ejemplo 10. Identificar si para el conjunto de los enteros ℤ la
operación binaria de suma definida como a + b es asociativa.
Solución: si es asociativa,, dado que:
a +( b + c ) = (a + b) + c
1 +( 2 + 3) = (1 + 2 ) +3
Elaboró: MC. Marcel Ruiz Martínez
2
6.1. Definición
Definici de operación binaria
Algebra universitaria
Ejemplo 8. Identificar si para el conjunto de los enteros ℤ la operación
binaria de resta definida como a - b es asociativa.
[El estudiante propone una solución]
9.- Complete
lete la siguiente tabla de forma tal que la operación
operaci binaria
sea conmutativa.
ACTIVIDAD NO ENTREGABLE (Si el profesor lo considera
pueden realizarse algunos ejercicios en clase)
Para los siguientes casos, determine si:
a.- La operación
ón puede definirse como una operaci
operación binaria.
b.- En caso de ser una operación
ón binaria identifique si es
ABIERTA o CERRADA bajo dicha operación.
1.- En el conjunto de los ℝ donde a * b es ab (multiplicaci
(multiplicación ordinaria)
10.- Considere la operación
ón binaria definida sobre el conjunto A = {a,
b, c, d} con una regla mostrada en la siguiente tabla:
2.- En el conjunto de los ℤ + (Enteros positivos o naturales) donde a*b
es a/b (división)
3.- En el conjunto de los ℤ + (Enteros positivos o naturales) donde a*b
es ab (potenciación)
4.- En el conjunto de los ℤ (Enteros) donde a*b es 2a + b.
operación binaria es
Para los siguientes ejercicios determine si la operaci
conmutativa o asociativa.
5.- En el conjunto de los ℤ + (Enteros positivos o naturales) donde a*b
es a + b + 2.
6.- En el conjunto de los ℤ (Enteros) donde a*b es bba (multiplicación
normal)
7.- En el conjunto de los reales ℝ -{0} (reales excepto el cero) donde a
* b es a/b (división ordinaria)
8-. En el conjunto de los reales ℝ donde a * b es ab/3
Elaboró: MC. Marcel Ruiz Martínez
Calcule:
i.
ii.
iii.
iv.
v.
vi.
vii.
viii.
c*d
d*c
b*d
d* b
a * (b * c )
(a * b ) * c
La operación binaria ¿Es conmutativa?
La operación binaria ¿Es asociativa?
3
6.1. Definición de operación binaria
Algebra universitaria
FUENTES DE INFORMACIÓN EN LÍNEA:
Introducción al cálculo y al álgebra, Volumen 3 Escrito por Open University (Milton Keynes, England)
http://books.google.com.mx/books?id=ELjhXQgM5e0C&lpg=PA40&dq=operaci%C3%B3n%20binaria&pg=PA39#v=onepage&q=operaci%C3%B3n%20binaria&f=false
Estructuras de matemáticas discretas para la computación Escrito por Bernard Kolman,Robert C. Busby,Sharon Ross
http://books.google.com.mx/books?id=7GJXRsNkglIC&lpg=PA334&dq=operaci%C3%B3n%20binaria&pg=PA330#v=onepage&q=operaci%C3%B3n%20binaria&f=false
Elaboró: MC. Marcel Ruiz Martínez
4