Corrientes genereadas por el viento
Anuncio

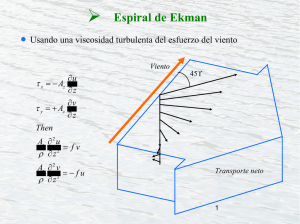
El efecto del viento viento témpanos Circulación General –– 2 efecto del viento 1 Circulación General –– 2 efecto del viento 2 La dinámica de Ekman (1905) • La mezcla vertical en el océano es causada por la turbulencia. • La mezcla turbulenta puede ser modelada como un proceso difusivo pero con un coeficiente de viscosidad varios órdenes de magnitud mayor que el molecular. • El equilibrio básico está dado por la mezcla turbulenta vertical inducida por el viento en la superficie y la rotación de la Tierra: 2 Ω sen ϕ u = Α/ρ ∂ 2v / ∂ z2 2 Ω sen ϕ v = Α/ρ ∂ 2u / ∂ z2 Ω es la velocidad angular de rotación de la Tierra, de modo que 2 Ω sen ϕ (el factor de Coriolis) es el doble de la componente local del vector rotación y ϕ la latitud, u y v son las componentes de la velocidad horizontal hacia el este (x) y norte (y), y z es la profundidad, positiva hacia abajo Α, el coeficiente de viscosidad turbulento debe ser determinado a partir de observaciones. Circulación General –– 2 efecto del viento 3 La solución de Ekman La solución es de la forma: [u , v] = Vo exp (‐ π z / D) [± cos (π/4 ‐ π z/D), sen (π /4 ‐ π z/D)] + en el HN ‐ en el HS El viento ha sido considerado de la dirección S (hacia el N), Vo = τ / ρ (A |f |)1/2 es la amplitud en superficie y D = π(2 A / | f |)1/2 es la escala vertical de decaimiento exponencial a la cual la dirección de la velocidad se invierte y τ es la tensión del viento en superficie De la elegante solución de Ekman surge: • • El vector velocidad horizontal rota en función de la profundidad en sentido horario en el HN y sentido antihorario en el HS El módulo disminuye formando así la llamada “espiral de Ekman” Circulación General –– 2 efecto del viento 4 Distribución vertical de velocidad [u , v] = Vo exp (-z π/ D) [cos (π/4 - z π /D), sen (π/4 -z π /D)] Circulación General –– 2 efecto del viento 5 Espiral de Ekman (HN) Circulación General –– 2 efecto del viento 6 Espiral de Ekman (HS) Circulación General –– 2 efecto del viento 7 Espiral de Ekman (HS) Transporte por unidad de distancia (m2 / s) τ = 0.1 Pa 0.08 ρ = 1026 Kg / m3 0.04 -4 A = 500 x 10 m / s 0 0.00 T = -0.97 m2 / s 10 70 150 80 60 90 300 250 200 120 130 140 110 100 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 50 100 40 50 30 -4 A = 100 x 10 m2 / s 20 -0.04 Velocidad N (m/s) 0 -0.10 -0.06 -0.02 0.02 Velocidad E (m/s) Espiral de Ekman para un océano de profundidad "infinita" en el Hemisferio Sur. La tasa de rotación y el módulo de la velocidad son funciones del coeficiente de viscosidad turbulento A. El transporte de masa sólo es función de la tensión del viento, la densidad y la latitud, por lo tanto es idéntica en ambos ejemplos. Circulación General –– 2 efecto del viento 8 El transporte de Ekman (HS) La integral vertical de la ecuación anterior, o el transporte de Ekman es: ∫ [ u , v ] dz = [ τ / ρ f, 0 ] El transporte de Ekman es a 90° de la dirección del viento. Esta característica tiene profundas consecuencias para la circulación general del océano y el clima. La magnitud y dirección del transporte de Ekman son consecuencia de las ecuaciones de conservación de cantidad de movimiento y son independientes del valor de A y de cualquier otro factor asociado a la turbulencia vertical. Circulación General –– 2 efecto del viento 9 Velocidad de Ekman (m/s) Espirales en el laboratorio -0.04 0.00 0.04 0.08 0 -0.08 -4 2 A = 100 x 10 m / s 160 Profundidad (m) 120 80 40 A = 500 x 10-4 m2 / s 200 u (m/s) v (m/s) 2 Transporte por unidad de distancia (m / s) τ = 0.1 Pa 3 = 1026 Kg / m 0.08 ρ 0.04 -4 A = 500 x 10 m / s 0 2 0.00 T = -0.97 m / s 10 70 60 150 80 300 290 280 270 260 250 240 230 220 210 200 190 180 170 160 150 140 130 120 110 100 90 50 100 40 50 30 -4 A = 100 x 10 m2 / s 20 -0.04 Velocidad N (m/s) 0 -0.10 -0.06 -0.02 0.02 Velocidad E (m/s) Circulación General –– 2 efecto del viento 10 Espirales en el océano real ‐ I de Price et al., Science, 1987 Circulación General –– 2 efecto del viento 11 Espirales en el océano real ‐ II Observaciones de una respuesta de tipo Ekman en la Corriente de California. Las corrientes medias observadas (izq) y dos espirales teóricas (der) usando diferentes difusividades eddy (274 y 1011 cm2/ s). Los números en los vectores son las profundidades en m. Los vectores mayores representan el viento medio. FIGURE 7.7 TALLEY Copyright © 2011 Elsevier Inc. All rights reserved Circulación General –– 2 efecto del viento 12 Viento y corrientes en la capa superior FIGURE 7.8 Tensión del viento en la superficie (rojo) y velocidad ageostrófica a 15 m de profundidad (azul) calculadas usando 7 años de datos de boyas derivantes y restando las velocidades geostróficas calculadas usando la distribución climatológica de densidad de Levitus et al. (1994a). (No se grafican vectores dentro de 5º de latitud del ecuador) TALLEY Copyright © 2011 Elsevier Inc. All rights reserved Circulación General –– 2 efecto del viento 13