POLIEDROS REGULARES: SLIDOS PLATNICOS Estrella

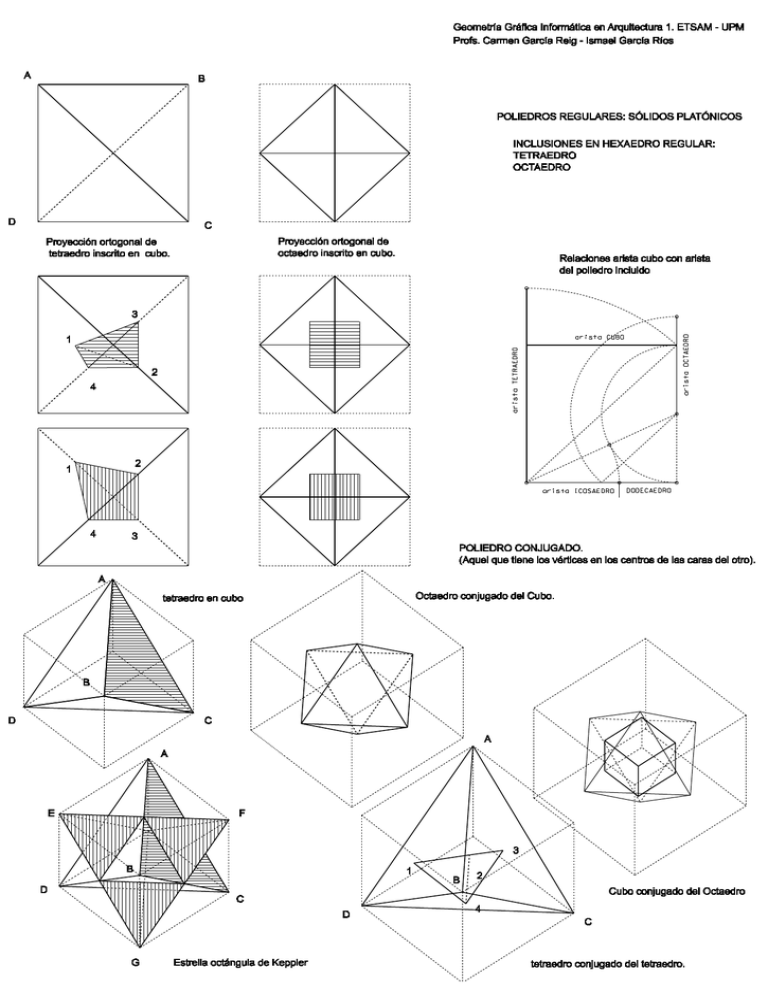
Geometra GrÆfica InformÆtica en Arquitectura 1. ETSAM - UPM
Profs. Carmen Garca Reig - Ismael Garca Ros
A
B
POLIEDROS REGULARES: SLIDOS PLATNICOS
INCLUSIONES EN HEXAEDRO REGULAR:
TETRAEDRO
OCTAEDRO
D
C
Proyeccin ortogonal de
Proyeccin ortogonal de
octaedro inscrito en cubo.
tetraedro inscrito en cubo.
Relaciones arista cubo con arista
del poliedro incluido
3
1
2
4
2
1
4
3
POLIEDRO CONJUGADO.
(Aquel que tiene los vØrtices en los centros de las caras del otro).
A
Octaedro conjugado del Cubo.
tetraedro en cubo
B
D
C
A
A
E
F
3
B
1
B
2
D
Cubo conjugado del Octaedro
C
D
4
C
G
Estrella octÆngula de Keppler
tetraedro conjugado del tetraedro.
Geometra GrÆfica InformÆtica en Arquitectura 1. ETSAM - UPM
ICOSAEDRO
DODECAEDRO
Profs. Carmen Garca Reig - Ismael Garca Ros
POLIEDROS REGULARES: SLIDOS PLATNICOS
INCLUSIONES EN HEXAEDRO REGULAR:
ICOSAEDRO
DODECAEDRO
Proyeccin ortogonal de icosaedro
y de dodecaedro inscrito en cubo.
1
1
2
2
Relaciones arista cubo con arista
5
3
3
del poliedro incluido
4
2
1
1
2
5
3
4
3
POLIEDRO CONJUGADO.
(Aquel que tiene los vØrtices en los centros de las caras del otro).
2
2
1
Posiciones de las aristas en las caras del cubo
3
1
5
3
4
2
1
3
2
5
1
4
3
Icosaedro
conjugado del Dodecaedro
Inclusin de dodecaedro en cubo
Dodecaedro
Inclusin de icosaedro en cubo
conjugado del Icosaedro
Geometra GrÆfica InformÆtica en Arquitectura 1. ETSAM - UPM
Profs. Carmen Garca Reig - Ismael Garca Ros
EQUIPARTICIONES ESPACIALES.
Asociaciones con poliedros regulares o semirregulares que compactan el espacio.
Poliedro de lord Kelvin
seccin principal
Kelvin
plano de truncamiento
plano de truncamiento
Octaedro
plano de truncamiento
poliedro de Kelvin
Asociacin de ocho Kelvin
Geometra GrÆfica InformÆtica en Arquitectura 1. ETSAM - UPM
Profs. Carmen Garca Reig - Ismael Garca Ros
POLIEDROS REGULARES: POLIEDROS VAC˝OS o VACUUS con aristas formadas por barras prismÆticas
1“ OPCIN: Una vez modelado el poliedro regular segœn su geometra, se copia y escala desde el centro geomØtrico O del
poliedro. Con la operacin Booleana: Diferencia, se resta el slido interior del exterior, conservando una copia del interior.
Separar un elemento en componentes mÆs simples, se separa el poliedro interior. Cortar slido segœn los vectores
ortogonales a cada cara.
SOLIDO: OCTAEDRO
SOLIDO: HEXAEDRO
O
COPIA escalada y centrada en O
Z
CORTAR slido segœn los vectores ABCD
O
C
B
O
DIFERENCIA de los slidos
D
A
X
Y
COPIA escalada al 90% y centrada en O
CORTAR slido segœn los vectores XYZ
OCTAEDRO VACUUS
DIFERENCIA de los slidos
HEXAEDRO VACUUS
COPIA escalada al 90% y centrada en O
DIFERENCIA del tetraedro exterior con el interior
DIFERENCIA con los prismas rectos con directrices las caras triangulos
TETRAEDRO VACUUS
2“ OPCIN: Una vez modelado el poliedro regular segœn su geometra, se copia y escala desde el centro geomØtrico O del poliedro.
Con la operacin Booleana: Diferencia, se resta el slido interior del exterior, conservando una copia del interior.
Separar un elemento en componentes mÆs simples, se separa el poliedro interior.
Cada cara del poliedro interior se extruye ortogonalmente
Diferencia, se resta cada prisma del poliedro exterior.
Geometra GrÆfica InformÆtica en Arquitectura 1. ETSAM - UPM
Profs. Carmen Garca Reig - Ismael Garca Ros
ALZADO
PLANTA
icosaecaedro vacus
obtencin del mdulo
slido
arista icosaedro
slido
cara=triÆngulo eqilÆtero
icosaedro vacus
icosaedro estrellado