Puertas lógicas NAND, NOR y OR exclusiva Práctica # 10

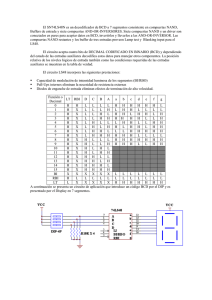
Grupo de investigación científica y microelectrónica
Puertas lógicas NAND, NOR y OR exclusiva
Práctica # 10
Objetivos
•
•
Estudiar la operación y uso de las compuertas NAND y NOR
Investigar la relación entre las entradas y las salidas de la puerta OR
exclusiva y de la compuerta or de equivalencia.
Equipo
• Modulo de LED Part N° 757
• CI 7400 Part N° 755
• Modulo de suiches Part N° 765
• CI 7404 Part N° 760
• Fuente DC Part No 767.
• Cl 7402 Part N° 761
• Cables.
• XOR CI 7486 par N° 762
INTRODUCCIÓN
Los circuitos digitales se construyen más frecuentemente con compuertas NAND y
NOR que con compuertas AND y OR. Las compuertas NAND y NOR son más
fáciles de fabricar con compuertas electrónicas y son las compuertas básicas
usadas en todas las familias de CI lógico digitales. Debido a la importancia de las
compuertas NAND y NOR en el diseño de circuitos digitales se han desarrollado
reglas y procedimientos para la conversión de funciones de Boole en términos de
AND, OR y NOT a diagramas lógicos equivalentes en NAND y NOR.
Práctica
Para la práctica se requiere:
•
1 CI 7404 (séxtupla inversor)
•
1 CI 7400 (cuádruple puerta NAND de 2 entradas)
•
1 CI 7402 (cuádruple puerta NOR de 2 entradas)
Diagrama de conexiones de los integrados
1
Grupo de investigación científica y microelectrónica
Figura1 Módulos integrados que contienen las compuertas NOR, INVERSOR y
NAND
1.
Monte el siguiente circuito
Mida con el osciloscopio los voltajes de salida para
a) Nivel lógico uno (LED encendido)
b) Nivel lógico cero (LED apagado).
Llene la siguiente tabla, combinando el estado de las entradas A y B
•
Exprese la señal de salida en términos de la entrada: F(A,B)
•
Que puede concluir acerca del montaje anterior. Esta correcto?.
2
Grupo de investigación científica y microelectrónica
2.
monte el siguiente circuito.
Mida con el osciloscopio los voltajes de salida para:
a) Nivel lógico uno (LED encendido)
b) Nivel lógico cero (LED apagado).
Llene la siguiente tabla, combinando el estado de las entradas A y B
•
Exprese la señal de salida en términos de la entrada: F(A,B).
•
Compare esta tabla la del ejercicio anterior.
•
A que conclusión llega?.
•
Esta bien el diagrama lógico del circuito mostrado?.
3.
monte el siguiente circuito.
Mida con el osciloscopio los voltajes de salida para:
a) Nivel lógico uno (LED encendido)
b) Nivel lógico cero (LED apagado).
Llene la siguiente tabla, combinando el estado de las entradas A y B.
3
Grupo de investigación científica y microelectrónica
•
•
•
Exprese la señal de salida en términos de la entrada: F(A,B)
Compare esta tabla la del ejercicio anterior.
A que conclusión llega?.
4.
Monte el siguiente circuito
Mida con el osciloscopio los voltajes de salida para:
a) Nivel lógico uno (LED encendido)
b) Nivel lógico cero (LED apagado
Llene la siguiente tabla, combinando el estado de las entradas A y B.
•
Exprese la señal de salida en términos de la entrada: F(A,B)
•
Compare esta tabla la del ejercicio anterior.
•
A que conclusión llega?.
•
Esta bien el diagrama lógico del circuito mostrado?
5.
Monte el siguiente circuito.
4
Grupo de investigación científica y microelectrónica
Llene la siguiente tabla, combinando el estado de las entradas A y B
•
Exprese la señal de salida en términos de la entra: F(A,B).
•
Exprese la señal de salida en términos de la entrada: F(A,B)
•
Compare esta tabla la del ejercicio anterior.
•
¿A que conclusión llega?
6.
Monte el siguiente circuito.
Llene la siguiente tabla, combinando el estado de las entradas A y B
•
Exprese la señal de salida en términos de la entrada: F(A,B)
•
Compare esta tabla la del ejercicio anterior.
•
A que conclusión llega?
5
Grupo de investigación científica y microelectrónica
ELEMENTOS ARITMETICOS DIGITALES
INTROUCCION
Un elemento aritmético es cualquier circuito que puede sumar, restar, multiplicar,
dividir o realizar alguna otra función aritmética con números binarios. Los
elementos aritméticos se encuentran en el ámbito de la tecnología de los
ordenadores y las calculadoras electrónicas. Los ordenadores y las calculadoras
electrónicas no son los únicos sistemas electrónicos digitales en los que se
realizan operaciones aritméticas, pero es en estas áreas donde se han
desarrollado los elementos aritméticos hasta su actual grado de versatilidad,
rapidez y sofisticación.
El tema de la aritmética binaria es muy vasto, habiéndole dedicado ya un capítulo,
por lo que en el presente únicamente se describen los conceptos básicos de la
suma, resta, multiplicación y división binaria, además de ofrecer ejemplos de
circuitos que realizan estas funciones.
CIRCUITOS ARITMETICOS EN FORMA DE CIRCUITO INTEGRADO
En general, cada uno de los circuitos aritméticos básicos está disponible en una
pastilla de CI. El sumador total fundamental, por ejemplo, puede obtenerse
típicamente en forma de 4 sumadores completos independientes, o como un
sumador de 4 bit capaz de sumar dos palabras binarias de 4 bit. Los sumadores
completos se combinan con otros circuitos de elementos lógicos dando lugar a
sumadores-restadores, multiplicadores y ALU, o unidades lógicas aritméticas de
uso múltiple. Estas unidades lógicas aritméticas (ALU) tienen la posibilidad de
realizar diversas operaciones lógicas y aritméticas. Cada cápsula de CI de estos
elementos contiene un equivalente a 75 ó 100 puertas lógicas discretas.
Quien va más allá en la integración de funciones múltiples en una sola pastilla es
el microprocesador. Estas pastillas LSI contienen toda la lógica clásica que existe
en el procesador central completo de un ordenador sencillo. El CI de un
microprocesador se vende juntamente con otros CI que realizan las funciones de
control, de entradas y salidas y funciones de memoria. El conjunto de estas
pastillas constituye un microordenador.
SUMA BINARIA
Para realizar la suma de dos números en forma binaria se utilizan las siguientes
reglas o algoritmos:
6
Grupo de investigación científica y microelectrónica
0+0=0
1+0=1
0+1=1
1 + 1 = 0 y llevo 1 (Carry)
ELEMENTOS ARITMETICOS DIGITALES
Estos algoritmos se aplican a cualquier suma binaria de números positivos. Por
ejemplo:
SEMISUMADOR
En la figura siguiente se representa un circuito lógico que puede emplearse para
realizar la suma binaria de acuerdo con los algoritmos de la pregunta anterior. El
mismo circuito básico puede construirse también utilizando una sola puerta XOR
(0-Exclusiva) y ambos actuarán siguiendo la misma tabla de verdad. Este circuito
es la base de cualquier sumador aritmético. Desgraciadamente, no genera una
señal de acarreo según el último algoritmo de suma indicado anteriormente.
Figura1 Circuito digital que opera como sumador medio
Para generar el acarreo o arrastre, el circuito se amplía con una puerta AND, que
detecta cuándo los dos sumandos A y B tienen nivel lógico 1 simultáneamente.
Este circuito, con la ampliación indicada, se muestra en la figura y se denomina
"semisumador".
SUMADOR COMPLETO O TOTAL
El semisumador debe modificarse más para que resulte útil en la mayoría de las
aplicaciones, puesto que si bien es adecuado para la suma de dos bit binarios, en
general los números constan de más de 1 bit. Se precisa un circuito sumador
independiente para sumar cada par de bit y poderse realizar la suma en paralelo.
Sin embargo, cuando se suma en paralelo, la posición de cada bit afecta a la
suma del bit de la izquierda:
7
Grupo de investigación científica y microelectrónica
1111 C (Acarreo)
+1001 A (Primer sumando)
1011 B (Segundo sumando)
10100
Figura2 Circuito digital que opera como sumador completo de dos bits
En el ejemplo precedente, cada sumador de 2 bits ha de ser modificado para
trabajar con 3 entradas: A, B y el arrastre C. Este circuito se denomina "sumador
completo" y se representa en la figura 3.
Figura3 Circuito digital que opera como sumador completo con carry de entrada
Práctica
1.
Tenga en cuenta el siguiente esquema
Figura 4 Circuito integrado que encapsula cuatro compuertas or exclusivas
8
Grupo de investigación científica y microelectrónica
2.
Construya el circuito semisumador de la figura siguiente
Figura 6 Sumador completo con carry de entrada
3.
Coloque los interruptores como se indica en la siguiente tabla:
4.
Complete la tabla de salida del sumador de la figura.
9
Grupo de investigación científica y microelectrónica
Informe
El informe de laboratorio debe incluir:
Las tablas con las respuestas de las compuertas.
Las funciones Booleanas que representan la acción del circuito lógico sobre los
estímulos.
El análisis y la explicación de las señales observadas.
El análisis de las discrepancias entre las señales que aparecen en los dibujos y
las medidas experimentalmente.
Conclusiones.
Causas de error.
10