REPRESENTACIÓN BINARIA - Departamento de Tecnología
Anuncio

REPRESENTACIÓN BINARIA
FC
Tema 1: REPRESENTACIÓN BINARIA
Contenido
*
Representación posicional de magnitudes. Bases y dígitos. Cambios de base.
*
Códigos binarios.
*
Representación binaria de números con signo.
*
Representación de números racionales: Punto fijo y punto flotante.
Bibliografía básica:
-
A.J. Molina et al: Cap 1
M. Morris Mano y Charles R. Kime: Cap 1
V. P. Nelson et al: Cap 1
J. Wakerly: Cap 2
C. Baena et al: Cap 1
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 1
REPRESENTACIÓN BINARIA
FC
REPRESENTACIÓN POSICIONAL DE MAGNITUDES EN BASE “r”
D Una magnitud entera Me se representa posicionalmente en base ‘r’ con n dígitos por:
Me = dn-1 dn-2 ... d1 d0 (r
debiendo cumplir:
n–1
Me = ∑ d j ⋅ r j
j=0
Los dígitos toman ‘r’ valores:
0, 1, ..., r-1
D Una magnitud fraccionaria Mf se representa
con dígitos a la derecha de un punto (que la
separa de la parte entera):
Mf = 0 . d-1 d-2 ... d-m (r
–1
Mf = ∑ d j ⋅ r j
Base 2 (binario): 0, 1 (bit)
Base 8 (octal): 0, 1, 2, 3, ... , 7
Base 16 (hexadecimal):
0, 1, 2, ..., 8, 9, A, B, C, D, E, F
j = –m
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 2
REPRESENTACIÓN BINARIA
FC
REPRESENTACIÓN POSICIONAL DE MAGNITUDES EN BASE “r”
D Una magnitud M con parte entera Me y parte fraccionaria Mf es la suma:
M = Me + Mf
D Se representa separadas por el punto fraccionario (o decimal):
M = dn-1 dn-2 ... d1 d0 . d-1 d-2 ... d-m (r
D y su valor es:
n–1
M =
∑
dj ⋅ r j
j = –m
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 3
REPRESENTACIÓN BINARIA
La representación con el menor número de dígitos de los 17 primeros números
FC
r = 10
r=2
r=3
r=4
r=8
r = 16
0
0
0
0
0
0
1
1
1
1
1
1
2
10
2
2
2
2
3
11
10
3
3
3
4
100
11
10
4
4
5
101
12
11
5
5
6
110
20
12
6
6
7
111
21
13
7
7
8
1000
22
20
10
8
9
1001
100
21
11
9
10
1010
101
22
12
A
11
1011
102
23
13
B
12
1100
110
30
14
C
13
1101
111
31
15
D
14
1110
112
32
16
E
15
1111
120
33
17
F
16
10000
121
100
20
10
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
S i e m p r e:
r = 10(r
Representación Binaria 4
REPRESENTACIÓN BINARIA
FC
Cambios de base. Decimal a base “r”: M(10 = ?(r
∗
Ejemplo: Problema 3. Representar el nº decimal 23.75 en las bases 2, 5, 6, 8 y 16.
•
Procedimiento para la parte entera, Me: Divisiones sucesivas
Base r:
•
r
coc1
d1
r
coc2
d2
•••
r
coc(n-2)
dn-2
Me(10 = dn-1dn-2...d2d1d0(r
r
dn-1
0 < dn-1 < r
Procedimiento para la parte fraccionaria, Mf = 0.fracc: Multiplicaciones sucesivas
Base r:
∗
Me
d0
0.fracc * r = d-1.fracc1 →
parte entera: d-1
0.fracc1 * r = d-2.fracc2 →
parte entera: d-2
0.fracc2 * r = d-3.fracc3 →
parte entera: d-3
0.fracc3 * r = d-4.fracc4 →
etc.
parte entera: d-4
Mf(10 = 0.d-1d-2d-3d-4···(r
¿Por qué funciona esto?
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 5
REPRESENTACIÓN BINARIA
FC
Cambios de base. Desde Base “r” a Decimal: M(r = ?(10
∗
Ejemplo: Problema 4. Convertir los siguientes números a base 10
a) 100.111010(2
b) 50(8
c) 101.1(2
d) 198F(16
c2) 101.1(5 ; c3) 101.1(100
•
Procedimiento: Se aplica directamente la expresión de la representación posicional
n–1
·
M = ∑ d j ⋅ r j = d n – 1 ⋅ r n – 1 + … + d 2 ⋅ r 2 + d 1 ⋅ r 1 + d 0 ⋅ r 0 + d –1 ⋅ r –1 + d –2 ⋅ r –2 + …
j = –m
•••
Conviene conocer las potencias de 2 {y de 16} para manejar números binarios
{y hexadecimales}
160 = 20 = 1
161 = 24
164 = 216
... 16k = 24·k
Dpto. Tecnología Electrónica, U. Sevilla.
162 = 28
Fundamentos de Computadores
163 = 212
Representación Binaria 6
REPRESENTACIÓN BINARIA
FC
Potencias de 2
n
2n =
n
2n =
n
2n =
n
2n =
0
1
6
64
12
4,096
18
262,144
1
2
7
128
13
8,192
19
524,288
2
4
8
256
14
16,384
20
1,048,576
= 1 Mega
3
8
9
512
15
32,768
21
2,097,152
= 2 Mega
4
16
10 1,024 = 1 Kilo
16
65,536
24
16,777,216
5
32
11
17
131,072
30
2,048
= 16 Mega
1 Giga
y las potencias negativas:
n
2n =
n
2n =
n
2n =
n
2n =
-1
0.5
-4
0.0625
-7
0.0078125
-10
0.0009765625
-2
0.25
-5
0.03125
-8
0.00390625
-20
0,95367431640·10-6
-3
0.125
-6
0.015625
-9
0.001953125
-30
0,9313225746·10-9
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 7
REPRESENTACIÓN BINARIA
FC
Cambios de base. Desde Base “r1” a Base “r2”
∗
En general, el procedimiento más sencillo consiste en pasar por decimal:
Sucesivamente:
M(r1 → M(10 → M(r2
∗
Excepciones: Cambio por agrupación/desagrupación de dígitos
•
Pasar de Base 2 (Binario) a Base 16 (Hexadecimal).
Ejemplo: Pasar 1010001.10101(2
•• Desde el punto fraccionario se agrupan los bits de 4 en 4 (añadiendo 0’s si hace
falta): 1010001.10101 = 101 0001 . 1010 1 = 0101 0001 . 1010 1000
•• Cada grupo de 4 bits se sustituye por el dígito Hexadecimal correspondiente:
0101 0001 . 1010 1000(2 → 5 1 . A 8(16
•
Pasar de Base 16 (Hexadecimal) a Base 2 (Binario). Ejemplo (Pr. 3): Pasar 198F(16
•• Cada dígito Hexadecimal se sustituye por los 4 bits correspondientes (y se eliminan los
0’s innecesarios si se desea):
198F(16 = 1 9 8 F(16 = 0001 1001 1000 1111(2 = 1 1001 1000 1111(2
∗ ¿Por qué funciona esto? Justifíquelo. Demuestre el procedimiento similar para convertir entre las bases 2 y 4, entre 2 y 8, y entre 4 y 16. ¿También entre 8 y 16?
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 8
REPRESENTACIÓN BINARIA
FC
Aritméticas en bases no decimales: El caso binario
Las 4 operaciones básicas (+, -, x , /) son similares al caso decimal salvo el valor de la base:
SUMA
Carry:
Sumando A:
Sumando B:
Resultado:
1100
0111
0110+
1101
MULTIPLICACIÓN
Multiplicando A: 0 1 1 0
Multiplicador B: x 0 1 0 1
0110
0000
0110
0000
Resultado: 0 0 1 1 1 1 0
Dpto. Tecnología Electrónica, U. Sevilla.
RESTA
Borrow:
0100
Minuendo A: 0 1 0 1
Sustraendo B: 0 0 1 1 Resultado:
0010
DIVISIÓN
Dividendo: 1 0 1 1 1 0 0: Divisor
-100
10
0011
Cociente
Resto
Fundamentos de Computadores
Representación Binaria 9
REPRESENTACIÓN BINARIA
FC
CODIFICACIÓN BINARIA
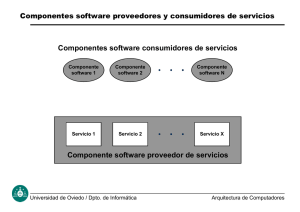
Dado un conjunto de ‘P’ elementos, la codificación binaria asigna valores
binarios a los elementos para representarlos usando sólo 0’s y 1’s.
∗
∗
Dos elementos distintos deben tener códigos binarios distintos
Un elemento puede tener más de un código binario
TIPOS
∗
NUMÉRICOS: Los elementos son números
•
•
Sistemas de numeración con base r = 2k (Bin, OCT, HEX)
Sistema decimal (BCD: Binary Coded Decimal): Representan los diez dígitos decimales
∗
ALFANUMÉRICOS: Los elementos son caracteres.
Veremos ASCII y UNICODE
∗
OTROS: Los elementos son variados.
Veremos: Gray (reflejado); Paridad; 7 segmentos; Imágenes en color;...
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 10
REPRESENTACIÓN BINARIA
FC
Generalidades
D Con ‘n’ bits se representan:
*
2n elementos distintos (2n son todas las cadenas posibles con ‘n’ ceros y unos)
*
Números representables (magnitudes): desde 0 hasta 2n - 1.
D Dados P elementos, el número mínimo de bits para representarlos es:
n = ⎡Log2(P)⎤
( ⎡x⎤ es el entero por exceso de x )
pero si se quiere representar un número (magnitud) de valor P, el mínimo es:
n = ⎡Log2(P+1)⎤
D Conceptos de codificación:
* Distancia entre dos palabras de código: número de bits distintos
* Adyacencia entre dos palabras de código: distancia unidad
* Código continuo: sus elementos tienen distancia unidad
* Código cíclico: Si es continuo y el primer y el último elemento son adyacentes
* Código simétrico: Si elementos simétricos tiene códigos simétricos
* Código ponderado (pesado): Cada bit tiene un peso según su posición
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 11
REPRESENTACIÓN BINARIA
FC
CÓDIGOS BINARIOS DECIMALES (BCD)
BCD
8421
Decimal
2421
Exceso 3
8 4 -2 -1
Biquinario
2 - de - 7
One hot
1 - de -10
0
0000
0000
0011
0000
0100001
0000000001
1
0001
0001
0100
0111
0100010
0000000010
2
0010
0010
0101
0110
0100100
0000000100
3
0011
0011
0110
0101
0101000
0000001000
4
0100
0100
0111
0100
0110000
0000010000
5
0101
1011
1000
1011
1000001
0000100000
6
0110
1100
1001
1010
1000010
0001000000
7
0111
1101
1010
1001
1000100
0010000000
8
1000
1110
1011
1000
1001000
0100000000
9
1001
1111
1100
1111
1010000
1000000000
Palabras
sin
emplear
10111- -
01-1
01110010-0
00000-0
11-1
111-
00-1
00111011-0
0000000
1100000
... ... ...
0000000000
Los que tienen
2 o más 1’s
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 12
REPRESENTACIÓN BINARIA
FC
Código ASCII
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 13
REPRESENTACIÓN BINARIA
FC
UNICODE ISO/IEC 10646 [Ver Morris&Kime]
* Código de 16 bits: %b15b14b13b12 b11b10b9b8 b7b7b5b4 b3b2b1b0b = $ H3H2H1H0
H3H2H1
H0
* Según $H3: 0-3: alfabetos, símbolos; 4-(9): Ideogramas); (9)-(D): Vacía; (D)-F: Restringida
* Contempla notaciones big-endian y little-endian
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 14
REPRESENTACIÓN BINARIA
FC
Código de Gray o reflejado
* Es un código simétrico, con distancia unidad y cíclico para 2n elementos
* Su construcción es:
Paso 1) Reflejar el de “n-1” bits;
Paso 2) Añadir el bit “n” como MSB, poniendo 0 en la parte superior y 1 en la inferior
n=1
Paso 1
0
1
n=3
n=2
{
Paso 1
Paso 2
0
1
1
0
00
01
11
10
Paso 2
00
01
11
10
10
11
01
00
000
001
011
010
110
111
101
100
* El código Gray de 4 bits es:
0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001 y 1000
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 15
REPRESENTACIÓN BINARIA
FC
Códigos de paridad
*
Para ganar en seguridad en la transmisión de la información se usan códigos
DETECTORES o CORRECTORES de fallos
*
Los códigos de PARIDAD son detectores de fallo en 1 bit
*
Formación del código: Sea P[n] = bb...b una palabra binaria de ‘n’ bits. Se genera un
bit de paridad, bp, de forma que la nueva palabra es de ‘n+1’ bits
Nueva palabra,
NP[n+1] = bpbb...b
** Paridad par: Se pone bp de forma que el número total de 1s en NP sea par. Así:
bp = 1 sii número_de_1s_en_P es impar
bp = 0 sii número_de_1s_en_P es par
** Paridad impar: Se pone bp de forma que el número total de 1s en NP sea impar:
bp = 0 sii número_de_1s_en_P es impar
bp = 1 sii número_de_1s_en_P es par
≠
Puede convenirse medir la paridad sobre los 0s de la palabra o poner bp en LSB. Pero son convenios distintos.
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 16
REPRESENTACIÓN BINARIA
FC
Código 7 segmentos
A
F
G
E
7 segmentos con encendido de LED activo en baja
B
C
D
Dpto. Tecnología Electrónica, U. Sevilla.
Q3 Q2 Q1 Q0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
Fundamentos de Computadores
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
A B C D E F G
0
1
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
1
0
1
1
0
1
0
0
1
0
0
1
0
0
1
0
0
0
0
1
0
1
0
1
1
1
0
1
0
0
0
0
0
0
0
0
0
1
1
1
0
0
0
1
0
1
0
0
0
1
0
0
1
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
Representación Binaria 17
REPRESENTACIÓN BINARIA
FC
Imágenes digitales en color
*
Cada imagen digital (monitor, impresora, etc.) se compone de muchos pixeles
*
Cada pixel logra el color combinando colores básicos según algunos formatos:
** CMYK: Cyan Magenta Yellow BlacK
** HLS: Hue (color, matiz), Saturation, Lightness
** RGB: Red Green Blue
*
Un ejemplo: los monitores y pantallas utilizan RGB. Para alta resolución (color
verdadero) usan 8 bits para intensidad de R, 8 para G y 8 para B
lo que da 224 ≈ 16 millones de colores distintos
Negro: $00 00 00; Blanco: $FF FF FF
Rojo al 100%: $FF 00 00; este mostaza: $FF 9E 00
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 18
REPRESENTACIÓN BINARIA
Espectro de la señal audible:
entre 20 Hz y 20KHz
RESOLUCIÓN:
Número ‘n’ de bits para cada valor.
Mayor ‘n’, da más calidad,
pero más volumen de información
Calidad CD: 16 bits/muestra
FRECUENCIA DE MUESTREO:
Mayor frecuencia da más calidad,
pero más volumen de información
Calidad CD: 44,1 KHz
Dpto. Tecnología Electrónica, U. Sevilla.
Señal
digital
codificada
Archivo
digital
Señal digital
Codificación
y Compresión
Señal tiempo
discreto
Conversión A/D
(cuantificador)
Señal
Analógica
Muestreo
Acondicionamiento de señal
Ondas
sonoras
Transductor
(micrófono)
FC
Sonido: Codificación digital de señal analógica
Fundamentos de Computadores
CODIFICACIÓN PCM:
Formatos WAV, AIFF, SU, AU, RAW,...
Tienen mucho volumen de información
COMPRESIÓN:
Formatos mp3, AAC, Ogg, FLAC,...
Tienen menor volumen de información
pero introducen pérdidas de calidad
Representación Binaria 19
REPRESENTACIÓN BINARIA
FC
NÚMEROS CON SIGNO
∗
La representación Decimal es signo-Magnitud (s-M), donde el signo es un carácter:
Ejemplo: Positivos: 41.625 o + 41.625; Negativos: - 41.625
∗
Caso Binario:el signo es un nuevo bit (MSB) llamado bit de signo (bs)
Convenio binario para s-M: Positivos: bs = 0; Negativos: bs = 1
Ejemplo:
1º Magnitud → Binario: 41.625(10 = 10 1001 . 101(2
2º Bit como bs MSB: + 41.625(10 = 010 1001 . 101(2
- 41.625(10 = 110 1001 . 101(2
∗
Propiedades: Hay dos ceros (+0 y -0) y con “n” bits representa [-(2n-1-1), 2n-1-1]
∗
El convenio binario s-M es muy poco eficiente. Hay que acudir a otros, como son:
∗ Convenio del Ca1: Está basado en la operación complemento a 1 (Ca1)
∗ Convenio del Ca2: Está basado en la operación complemento a 2 (Ca2)
∗ Exceso-K o sesgado (biased): Basado en añadir una cantidad K
frecuentemente K = 2n-1 , ,o K = 2n-1 - 1
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 20
REPRESENTACIÓN BINARIA
FC
Complemento a “r” y a “r-1”
Para “n” dígitos y base “r”, dada una palabra de magnitud M ( M= dn-1 dn-2 ... d1 d0(r), se
definen las siguientes operaciones unarias:
Definición 1. Operación complemento a “r” de M
n
Car ( M ) = r – M
n
mod r
Definición 2. Operación complemento a “r-1” de M1
n
Ca ( r – 1 ) ( M ) = ( r – 1 ) – M
n
mod r
Propiedades: Particularizamos a r = 2, complemento a 2 (Ca2) y complemento a 1 (Ca1)
∗
Ca2(M) = Ca1(M) + 1
∗
Ca2 [Ca2(M)] = M; también, Ca1 [Ca1(M)] = M
∗
Ca2(0) = 0; pero Ca1(0) = 1...11 = 2n-1
∗
Ca2(2n-1) = 2n-1
1.Para M con parte fraccionaria de “m” bits, esto cuyo LSB es b-m, en vez de restar 1 a rn debe restarse el peso del LSB. Esto es, Ca(r-1) (M) = rn -r-m-M|mód r**n
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 21
REPRESENTACIÓN BINARIA
FC
Ejemplos y Reglas de construcción de Ca1 y de Ca2
Para r = 2 y n = 8, obtener el Ca2 de M1= 0011 1010 y de M2= 1100 1010
Ejemplo 1. Obtener el Ca1 de M1= 0011 1010 y de M2= 1100 1010
Sol: Ca1(0011 1010) = 1100 0101
Ca1(1100 1010) = 0011 0101
Regla: Cada bit de M se complementa para dar el correspondiente bit de Ca1(M)
Ejemplo 2. Obtener el Ca2 de M1= 0011 1010 y de M2= 1100 1010
Sol: Ca1(0011 1010) = 1100 0110
Ca1(1100 1010) = 0011 0110
Regla 1: Aplicar la definición operando con aritmética binaria
Regla 2: Obtener Ca1 y sumarle 1
Regla 3: Comenzando por la derecha (LSBs) dejar igual todos los 0s y el primer 1.
Después, complementar los restantes bits (yendo hacia MSB)
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 22
REPRESENTACIÓN BINARIA
FC
Convenio de representación de números con signo
Sea N un número binario con signo, cuya magnitud es M (M = |N| = bn-2···b1b0).
Ca1
El convenio de representación en Ca1 añade un bit de signo como MSB, asignando:
* Si N > 0, N → 0bn-2···b1b0
* Si N < 0, N → Ca1(0bn-2···b1b0) = 1bn-2···b1b0
Propiedad: Hay dos ceros (+0 y -0) y con “n” bits representa [-(2n-1-1), 2n-1-1]
Ca2
El convenio de representación en Ca2 es similar:
* Si N > 0, N → 0bn-2···b1b0
* Si N < 0, N → Ca2(0bn-2···b1b0)
{ → 1b...bb }
Propiedades: A diferencia de s-M y Ca1, en Ca2 sólo hay un cero (0), pero no hay simetría
en la representación ya que con “n” bits representa: [- 2n-1, 2n-1-1]
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 23
REPRESENTACIÓN BINARIA
FC
Exceso-K o sesgado (biased)
* Se suma la cantidad K al número con signo, N: N → (N+K)(2
El valor de K es frecuentemente 2n-1
{o, como sucede en el estándar IEEE-754, [2n-1 - 1]}.
*
Diferencias entre ambos valores de K: 1/el rango; y 2/si el 0 es positivo o negativo
Ejemplo para 3 bits: K es 23-1 = 4 {o K es 3}
Decimal
K=4
Decimal
K=3
4
111
3
111
3
110
2
110
2
101
1
101
1
100
0
100
0
011
-1
011
-1
010
-2
010
-2
001
-3
001
-3
000
-4
000
-4
Dpto. Tecnología Electrónica, U. Sevilla.
Este 0 es positivo
Fundamentos de Computadores
Este 0 es negativo
Representación Binaria 24
REPRESENTACIÓN BINARIA
FC
Notaciones para números con signo de 4 bits
Decimal a Binaria
Binario a decimal
Decimal
s-M
Ca1
Ca2
Exceso 2m-1
Binario
Si s-M
Si Ca1
7
0111
1111
0000
0
6
0110
1110
0001
1
5
0101
1101
0010
2
4
0100
1100
0011
3
3
0011
1011
0100
4
2
0010
1010
0101
5
1
0001
1001
0110
6
7
+ 0 (- 0)
Si Ca2
0000 (1000)
0000 (1111)
0000
1000
0111
-1
1001
1110
1111
0111
1000
-0
-7
-8
-2
1010
1101
1110
0110
1001
-1
-6
-7
-3
1011
1100
1101
0101
1010
-2
-5
-6
-4
1100
1011
1100
0100
1011
-3
-4
-5
-5
1101
1010
1011
0011
1100
-4
-3
-4
-6
1110
1001
1010
0010
1101
-5
-2
-3
-7
1111
1000
1001
0001
1110
-6
-1
-2
-8
---------
---------
1000
0000
1111
-7
-0
-1
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 25
FC
REPRESENTACIÓN BINARIA
PROBLEMA 10. Represente con el mínimo nº de bits posibles los siguientes números decimales en notación binaria, signo-magnitud, complemento a 1 y complemento a 2:
a) ± 122;
b) ± 64;
c) ± 15;
d) ± 37
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 26
REPRESENTACIÓN BINARIA
FC
REPRESENTACIÓN DE NÚMEROS RACIONALES
•
PUNTO FIJO: Basada en la notación posicional
Punto en posición fija
N(B = dn-1 dn-2 ... d1 d0 . d-1 d-2 ... d-m
dn-1 dn-2 ... d1 d0 d-1 d-2 ... d-m
parte entera . fraccionaria
•
PUNTO FLOTANTE: Basada en la notación exponencial o científica
N = man • B
ex
man
mantisa (con signo)
Base
exponente (con signo)
Dpto. Tecnología Electrónica, U. Sevilla.
ex
La Base no se almacena, se acuerda cuál es
Fundamentos de Computadores
Representación Binaria 27
REPRESENTACIÓN BINARIA
FC
NOTACIÓN EN PUNTO FIJO
•
Cuantización:
•
•
•
Rango:
•
•
•
Es la diferencia de valor de un número representable al siguiente
En este caso es fija y coincide con el peso del LSB, B-m
Es el intervalo entre el menor y el mayor número representable
Suponiendo base B = 2 y que para los números con signo se usa la notación Ca2,
vale
[- 2n-1, +(2n-1 - 2-m)]
Aproximaciones por TRUNCACIÓN o REDONDEO:
•
Al limitar el nº de bits fraccionarios (p.ej., 8) el valor representado es una aproximación de N
N = b ... bbb,0110 0111 bbb...
TRUNCACIÓN
N1 = b ... bbb,0110 0111 0bb...
b ... bbb 0110 0111
b ... bbb 0110 0111
REDONDEO
N2 = b ... bbb,0110 0111 1bb....
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
b ... bbb 0110 1000
Representación Binaria 28
REPRESENTACIÓN BINARIA
FC
NOTACIÓN EN PUNTO FLOTANTE
•
Como la notación científica, sirve para representar rangos muy amplios de números:
Ejemplos en decimal:
•• -77,26171875 = - 0,7726171875 · 102 = - 7726171875 · 10-8
••
qe- = -1,602 · 10-19 = - 0,000 000 000 000 000 000 160 2 · 100
•• 3 · 1011 = 300 000 000 000 · 100
•
La cuantización es variable y se adapta al valor del número representado
•
Base: Podría ser cualquiera, pero aquí utilizaremos B = 2 (binario) [B = 10 si decimal]
•
Representación binaria: “man” y “ex” se representarán con bits, en binario o en BCD
•
Normalización: Es necesaria para que cada número tenga una sola representación
•• Entera: La mantisa es man = dn-1 dn-2 ... d0. con dn-1 ≠ 0
•• Fraccionaria pura: La mantisa es man = 0. d-1 d-2 ... con d-1 ≠ 0
•• Fraccionaria IEEE-754: La mantisa es man = 1. b-1 b-2 ...
→ Las normalizaciones entera y fraccionaria pura se usan en FC; usan bases 2 y 10 (BCD)
→ La normalización Fraccionaria IEEE-754 es un estándar y sólo vale para base 2
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 29
REPRESENTACIÓN BINARIA
FC
NOTACIÓN EN PUNTO FLOTANTE fraccionaria pura (FC)
•
Convenios:
•• “man” y “ex” se representan en signo-Magnitud
•• El tamaño de la palabra (nº de bits para “man” y para “ex”) y el orden (si se escribe
[sman man sex ex] o [sex ex sman man] o otras formas) no están preestablecidos
(hay que ver/explicar cada caso)
•• El cero es especial: 00...00; el infinito, también, + 11...11
•
Ejemplo: Con 32 bits (24 smanman y 8 sex ex), representar N = 53.2874(10
•• En BCD: N = 53.2874(10 =normalizado= 0.532874 · 102
Representación [sman man sex ex]:
0 0101 0011 0010 1000 0111 010 0 000 0010
•• En binario: N = 53.2874(10 =binario= 11 0101 . 0100 1001 1001 0011 0000 1011 1110...(2 =
=normalizado= 0 . 110 1010 1001 0011 0010 0110 0001 0111 110... · 26 =
=(24-1)bits = 0 . 110 1010 1001 0011 0010 0110 · 26
Representación [sman man sex ex]:
Dpto. Tecnología Electrónica, U. Sevilla.
0 110 1010 1001 0011 0010 0110 0 000 0110
Fundamentos de Computadores
Representación Binaria 30
REPRESENTACIÓN BINARIA
NOTACIÓN EN PUNTO FLOTANTE estándar IEEE-754 simple precisión
FC
El “1,” está oculto
Exponente con signo EXCESO 127
N = ± ( 1, manf ) ( 2 ) • 2
signo + (0) o - (1)
ex
Mantisa: signo-Magnitud (manf)
s
1
ex + 127
8
[8]
manf [23]
23
Valores representados:
s
Números normales:
ex +127
0/1 [1,254]
manf
cualquiera
+0 y -0
0/1
0000 0000
0000 0000 0000 0000 0000 000
+∞ y -∞
0/1
1111 1111
0000 0000 0000 0000 0000 000
Desnormalizados
0/1
0000 0000
≠0
0/1
1111 1111
≠0
NaN
Dpto. Tecnología Electrónica, U. Sevilla.
Orden: signo exponente manf
Fundamentos de Computadores
Representación Binaria 31
REPRESENTACIÓN BINARIA
FC
ENLACES SOBRE IEEE-7541
* Para pasar de decimal a estándar:
http://babbage.cs.qc.edu/IEEE-754/Decimal.html
* Para pasar del estándar a decimal:
http://babbage.cs.qc.edu/IEEE-754/32bit.html
*Aquéllo que siempre quisiste saber y nunca te atreviste a preguntar sobre el estándar.
http://babbage.cs.qc.edu/courses/cs341/IEEE-754references.html
1.Al menos a mi, me llegaron mediante Pilar Parra.
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 32
REPRESENTACIÓN BINARIA
FC
EJEMPLOS IEEE-754
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 33
FC
REPRESENTACIÓN BINARIA
Dpto. Tecnología Electrónica, U. Sevilla.
Fundamentos de Computadores
Representación Binaria 34