Campos Variantes con el tiempo y ecuaciones de Maxwell
Anuncio

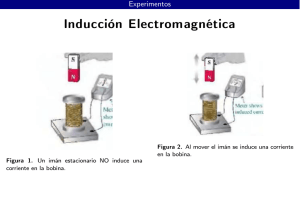
Campo variantes en el tiempo & ecuaciones de Maxwell Supuesto básico de Faraday Faraday, partía de la creencia de que si una corriente podia producir efectos magneticos, entonces efectos magnéticos podian producir corrientes. Experimento de Faraday “Enrrolló dos alambres separados alrededor de un toroide de hierro y colocó un galvanometro en un circuito y en el otro una batería. Al cerrar el circuito observó una deflexión en el galvanometro, una deflexión similar pero en sentido contrario cuando se desconectaba la bateria ……” Ley de Faraday dΦ fem = − V dt Un campo magnético que varia con el tiempo produce una fuerza electromotriz (fem) capaz de producir una corriente en un circuito cerrado adecuado. Una fem, es un voltaje que proviene o de conductores que se mueven en un campo, o que están bajo la influencia de un campo magnético que cambia en el tiempo. Un valor diferente de dφ/dt puede deberse a: • Un flujo que cambia con el tiempo, y que atraviesa el area que es circundada por una trayectoria cerrada. • Una trayectoria cerrada, que se desplaza en el espacio, en donde existe un flujo estable. • Una combinación de las dos circunstancias anteriores. dΦ fem = − N dt Φ es el flujo que atraviesa las N espiras. El signo menos indica que fem tiene una dirección tal que produce una corriente cuyo flujo, si se suma al flujo original, reduciria la magnitud de la fem. Este enunciado se corresponde con la Ley de Lenz. r r r r fem = ∫ E ⋅ dL = ∫ ∇xE ⋅ dS S r r Φ = ∫ B ⋅ dS S r r ∂B ∇x E = − ∂t dΦ d r r = ∫ B ⋅ dS dt dt S d r r ⇒ fem = − ∫ B ⋅ dS dt S r r ∂B ∇x E = − ∂t Forma punto o forma diferencial. Ecuación de Maxwell, que define las relaciones entre un campo eléctrico y un campo magnético variable en el tiempo. Esta ecuación de Maxwell, es la misma Ley de Faraday, en términos de campos eléctricos y magnéticos y no de voltages, corrientes y flujos. La ecuación de ampѐre, presenta contradicciones, cuando se trata de evaluar campos que varian en el tiempo. r r ∇xH = J r r ∇ ∇xH = ∇J = 0 ( ) r ∂ρ v ∇J = − ∂t Maxwell dedujo un término, que elimina la contradicción, le encontró un significado físico y predijo consecuencias, la mas importantes, las onda electromagneticas. La corriente de desplazamiento r ∂D ∂t Al término, que encontró Maxwell, lo denominó, corriente de desplazamiento. r r r ∂D ∇xH = J + ∂t Otras de las ecuaciones de Maxwell !!!!! r ∂ r r r I d = ∫ J d ⋅ dS = ∫ D ⋅ dS s ∂t s r r I d = ∫ J ⋅ dS s r r H ⋅ d L = I + I d ∫ r r ∂B ∇xE = − ∂t r r r ∂D ∇xH = J + ∂t r ∇D = ρ v r ∇B = 0 r r D = εE r r B = µH r r J = σE r r J = ρvv r r r D = ε0E + P r r r B = µ0 H + M r r P = χ eε 0 E r r M = χmH ( ) Forma integral r r r ∂B ∫ E ⋅ dL = −∫s ∂t r r r ∂D ∫ H ⋅ dL = I + ∫s ∂t r r ∫s DdS = ∫vol ρv dv r r ∫ BdS = 0 s Ley de Faraday Ley de Ampѐre modificada por Maxwell. Leyes de Gauss.