Práctica 4 Probabilidad y dependencia estadística En esta

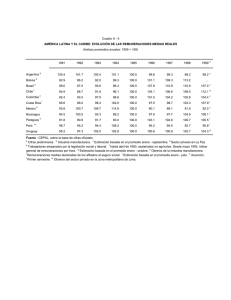
Práctica 4
Probabilidad y dependencia estadística
En esta práctica se continúa avanzando en los procedimientos para el análisis de datos de
encuesta mediante el uso de PSPP a la vez que se indaga en el uso de la noción de probabilidad
para la determinación de relaciones entre variables.
Con esta práctica se pretende que el alumno afiance los conceptos de suceso dependiente e
independiente y su relación con la teoría de probabilidades. Con este acercamiento empírico
se abre también la puerta a nociones de dependencia e independencia estadística que son
centrales en la investigación de fenómenos sociales.
Vamos a comenzar indagando en lar relación que existe entre sexo y nivel de estudios, y más
adelante nos preguntaremos por la relación que existe entre Status y Voto Político.
Como en la práctica anterior habíamos generado el fichero activo “SAV”, ahora simplemente
desde PSPP le indicaremos Archivo y luego Abrir
Recordemos que se llamaba CIS2927.SAV y cuyo path era: [K:\CIS\CIS2927.SAV]
Una vez llamado el fichero vamos a solicitar la distribución de frecuencias de las siguientes
variables
-Sexo (P29)
-Estudios (ESTUDIOS) Esta variable, se encuentra en la parte final del fichero, ha sido generada
por el CIS, mediante la combinación de las preguntas P31 y P31a.
Para pedir dicha distribución, recordemos la secuencia Analizar: Estadística Descriptiva:
Frecuencias
Llevamos ambas variables a la caja, y como son nominales, desmarcamos todos los
estadísticos.
La distribución que obtenemos es la siguiente:
Con dicha información podemos calcular las siguientes probabilidades
P(Mujer)=1270/2480=0,5121
P(Superiores)=278/2480=0,1121
Si ahora nos preguntamos cuál es la probabilidad de encontrar en una selección aleatoria a una
mujer con estudios Superiores deberemos suponer que el hecho de ser mujer no tiene relación
con el nivel de estudios alcanzado. Es decir que hay independencia entre ambas variables.
Recordemos que la probabilidad de ocurrencia conjunta de dos sucesos independientes es el
producto de ambas probabilidades. En este caso el producto de la probabilidad de seleccionar
a una mujer por la probabilidad de seleccionar a alguien con estudios superiores.
P( S(Mujer)  S(Superiores) )= P(Mujer) P(Superiores)
En nuestro caso P( S(Mujer)  S(Superiores) ) = 0,5121x0,1121=0,0574
De forma análoga podríamos pensar en la probabilidad conjunta de ser hombre con estudios
superiores, en nuestro caso P( S(Hombre)  S(Superiores) ) = 0,4879x0,1121=0,0547
Vamos ahora a comprobar mediante la distribución conjunta entre las variables sexo y
estudios si nuestro supuesto es cierto. Para ello vamos a Analizar: Estadística Descriptiva y
seleccionamos en este caso Tablas Cruzadas
En filas vamos a colocar la variable ESTUDIOS y en columnas la variable P29 (sexo del
entrevistado). Conviene que en Estadísticos... que desmarque todos y en el botón Celdas...
asegúrese de que esté marcado Total –que son los porcentajes sobre el total de la tabla-. Los
resultados se presentan en una tabla:
En cada una de las celdas nos indica la frecuencia –número de casos-, el porcentaje en la
dirección de las filas, el porcentaje en la dirección de las columnas, y el porcentaje sobre el
total de casos (n=2480).
Si observamos por ejemplo la casilla de Mujeres con estudios Superiores vemos que hay 132
entrevistadas, que suponen el 47,5% de quienes tienen estudios superiores (132/278), y un
10,9% del conjunto de mujeres (132/1210). Las 132 mujeres con estudios superiores suponen
el 5,3% de la muestra (132/2480).
Este último valor 0,053 es la probabilidad de selección al azar de una mujer con estudios
superiores. Recordemos que bajo el supuesto de independencia esperábamos una
probabilidad de 0,057. Es decir la probabilidad es menor.
En el caso de los hombres encontramos que la probabilidad es 0,059 cuando esperábamos
0,055.
Las diferencias observadas son pequeñas, podemos suponer que el efecto combinado entre
sexo y nivel de estudios resulta reducido, si bien es importante señalar que dicho efecto es
positivo para los hombres, hay una mayor probabilidad de tener estudios superiores por ser
hombre que por ser mujer.
Recordemos que cuando dos sucesos no son independientes y son condicionados:
P( S(Mujer)  S(Superiores) )= P(Mujer) P(Superiores/Mujer)
En nuestro caso: 0,053=0,5121x P(Superiores/Mujer)
La probabilidad condicionada de tener estudios Superiores cuando se es mujer será:
P(Superiores/Mujer)=(0,053/0,5121)=0,1035
De forma análoga para los hombres:
P( S(Hombre)  S(Superiores) )= P(Hombre) P(Superiores/Hombre)
En nuestro caso: 0,059=0,4879x P(Superiores/Hombre)
La probabilidad condicionada de tener estudios Superiores cuando se es mujer será:
P(Superiores/Hombre)=(0,059/0,4879)=0,1209
Si bien la interacción entre género y estudios superiores no es elevada si que se puede decir
que comparativamente ser hombre ayuda a tener un nivel de estudios más elevado1
1
Si bien supera con creces el propósito de este ejercicio, podemos observar que la relación (ratio) entre
probabilidades condicionadas de Hombres respecto mujeres es (
comparativa que por ser hombres tienen para tener estudios superiores.
)
que es la ventaja
(Evidentemente el sexo no explica el nivel de estudios alcanzado, la explicación deviene en las
diferencias sociales que penalizan relativamente el acceso a las mujeres a estudios superiores).
Vamos ahora a explorar otra relación entre variables. Estatus Social y Posicionamiento
ideológico. La variable Estatus Social se encuentra al final del fichero y es una variable
generada por el propio CIS a partir de las preguntas de ocupación y de estudios. La variable de
posicionamiento ideológico vamos a construirla a partir de la pregunta 27.
Dicha pregunta posiciona entre la Izquierda y la Derecha a los entrevistados. Es una variable de
intervalo. Podemos obtener la distribución de frecuencias de dicha variable:
En este caso queremos transformar esta variable en tres categorías: Izquierda, Centro y
Derecha. De forma que
Valores entre 1 y 3 sean Izquierda
Valores entre 4 y 7 sean Centro
Valores entre 8 y 10 sean Derecha
Para realizar la transformación podemos ejecutar en el fichero de sintaxis la siguiente
secuencia de comandos:
****Generación de la variable ideología política IDEO mediante agrupamiento de P27.
****Con COMPUTE copiamos la variable.
****Con recode recodificamos los valores.
****Declaramos valores missing con MISSING VALUE y etiquetamos la variable IDEO con VALUE LABELS.
COMPUTE IDEO=P27.
RECODE IDEO (1 THRU 3=1) (4 THRU 7=2) (8 THRU 10=3).
MISSING VALUES IDEO (98,99).
VARIABLE LABELS IDEO “Posición Ideológica”
VALUE LABELS IDEO 1 “Izquierda” 2 “Centro” 3 “Derecha”.
De los comandos anteriores el único nuevo es RECODE. Se ha utilizado de una forma simple,
en la que indicamos el nombre de variable a recodificar IDEO y mediante la expresión THRU
indicamos que Desde 1 a 3, ahora se convierten en código 1; desde 4 a 7 en código 2...
P27
IDEO
THRU
1
2
3
4
5
6
7
8
9
10
98
99
1
2
3
Missing
La variable de salida tendrá 3 códigos. Lo anterior podemos hacerlo también desde el menú de
PSPP, accediendo en la barra superior a Transformar, Recodificar en Variables Diferentes
Seleccionamos la variable P27, luego pulsamos el botón valores viejos y nuevos
Vamos rellenando en la opción intervalo, los valores viejos, e indicando el valor nuevo,
pulsamos Añadir y repetimos la veces que sean necesarias.
Para introducir los valores perdidos (98 y 99) en Nuevo Valor seleccionamos la opción Perdido
por el Sistema
Después de Añadir pulsamos Continuar, al volver a la pantalla anterior escribimos el nuevo
nombre de variable IDEO y su etiqueta y pulsamos el botón de Cambio
Después finalmente Aceptar. Si elegimos esta opción, deberemos etiquetar los valores de la
nueva variable, accediendo a la misma por la pestaña de Vista de Variables, abajo de la rejilla
de datos, y seleccionando la variable introducirlos manualmente:
Después de Añadir las veces necesarias, pulsamos Aceptar.
(Recuerde, después de ejecutar transformaciones en el conjunto de datos conviene que grabe
el fichero activo (SAV) para conservar estas transformaciones para próximas sesiones).
Ahora estamos en condiciones de trabajar con la variable STATUS e IDEO. Vamos a comenzar
solicitando la distribución de frecuencias así como la tabla con el cruce de ESTATUS e IDEO.
Los resultados anteriores nos permiten obtener las probabilidades de cada suceso:
Izquierda
Centro
Derecha
TOTAL
0,2613
0,6373
0,1014
1
Clase alta/media-alta
Nuevas clases medias
Viejas clases medias
Obreros cualificados
Obreros no cualificados
No consta
TOTAL
0,1867
0,1992
0,1657
0,3000
0,1282
0,0202
1
A partir de los resultados anteriores podemos construir la tabla, bajo el supuesto de
independencia. Es decir el producto de las probabilidades de cada suceso:
Clase alta/media-alta
Nuevas clases medias
Viejas clases medias
Obreros cualificados
Obreros no cualificados
No consta
Izquierda
0,049
0,052
0,043
0,078
0,033
0,005
Centro
Derecha
0,120
0,127
0,106
0,191
0,082
0,013
0,019
0,020
0,017
0,030
0,013
0,002
Las probabilidades observadas empíricamente, las obtenemos de la encuesta:
Clase alta/media-alta
Nuevas clases medias
Viejas clases medias
Obreros cualificados
Obreros no cualificados
No consta
Izquierda
0,062
0,052
0,035
0,085
0,023
0,005
Centro
Derecha
0,122
0,140
0,100
0,178
0,085
0,010
0,017
0,020
0,028
0,021
0,013
0,003
Podemos ahora preguntarnos el efecto que tiene la clase social en la ideología. Por ejemplo
respecto a la Derecha. Para ello calculamos las probabilidades condicionadas de declararse de
izquierda por clase social. Por ejemplo en el caso de la “Clase alta/Media-alta”
P( S(Alta)  S(Derecha) ) = P(Alta) P(Derecha/Alta)
En nuestro caso: 0,017=0,1867 x P(Derecha/Alta)
P(Derecha/Alta)=0,017/0,1867=0,091
Procediendo de forma idéntica obtenemos las demás:
Clase alta/media-alta
Nuevas clases medias
Viejas clases medias
Obreros cualificados
Obreros no cualificados
No consta
Derecha
0,091
0,100
0,169
0,070
0,101
0,149
Como podemos observar las Viejas clases medias tienen una mayor propensión a posicionarse
en la derecha mientras que los Obreros Cualificados son el grupo que menos lo hace. La
relación (ratio) es que las Viejas Clases Medias lo hacen (
Cualificados.
)
mayor que los Obreros