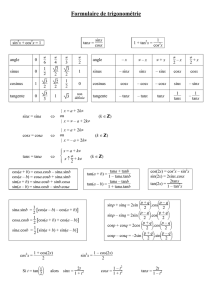
FORMULES DE TRIGONOMÉTRIE
Anuncio

FORMULES DE TRIGONOMÉTRIE Lignes trigonométriques des arcs remarquables : x sin x cos x tan x 0 0 1 0 si x cos²(x) + sin²(x) = 1 . /6 1/2 /4 2/2 2/2 1 3/2 3/3 /3 3/2 1/2 3 sin x [ ] : tan x = 2 cos x Formules relatives aux arcs associés : /2 1 0 \\\\\\\\\\\\\\ 1 + tan²(x) = 1 = tan’ (x) cos²(x) cos (-x) = cos x sin (-x) = - sin x si x 2 [] : tan (-x) = - tan x cos (-x) = - cos x sin (-x) = sin x si x 2 [] : tan (-x) = - tan x cos (+x) = - cos x sin (+x) = - sin x si x 2 [] : tan (+x) = tan x cos ( 2 – x ) = sin x sin ( 2 - x ) = cos x si x 0 [] : tan ( 2 – x ) = cotan x cos ( 2 + x ) = - sin x sin ( 2 + x ) = cos x si x 0 [] tan ( 2 + x ) = - cotan x : Formules d’addition : cos (a+b) = cos a cos b – sin a sin b sin (a+b) = sin a cos b + cos a sin b cos (a-b) = cos a cos b + sin a sin b sin (a-b) = sin a cos b – cos a sin b Si a 2 [] et b 2 [] et (a+b) 2 [] : tan a + tan b tan (a+b) = 1 - tan a tan b Si a 2 [] et b 2 [] et (a-b) 2 [] : tan a - tan b tan (a-b) = 1 + tan a tan b Lignes trigonométriques de l’arc double : cos ( 2a ) = cos²(a) - sin²(a) = 2 cos²(a) - 1 = 1 – 2 sin²(a) sin( 2a ) = 2 sin a cos a Si a 2 [] : 2 tan a sin( 2a ) = 1 + tan²(a) Si a 2 [] cos ²(a) = 1 - tan²(a) cos ( 2a ) = 1 + tan²(a) et (2a) 2 [] : 1 + cos(2 a) 2 2 tan a tan (2a) = 1 - tan²(a) sin ²(a) = 1 - cos(2 a) 2 Pour se tester ... cos ² a + sin² a cos(a+b) cos(a-b) sin(a+b) sin(a-b) cos(2a) sin(2a) supprimer le carré de cos²(a) supprimer le carré de sin²(a) tan(a+b) 1 + tan²(a) tan’(a) tan(a-b) tan(2a) cos ( /3) sin(/3) cos(+x) cos(-x) tan( /4) sin ( x + /2) Score /20