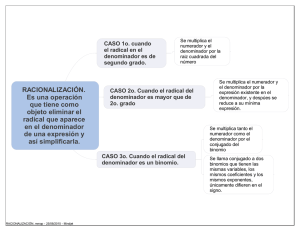
B.8 Racionalizacion de un monomio y binomio

Materia: Matemática de Tercer Año
Tema: Racionalización de monomios y binomios
Al sumar y restar expresiones radicales, podemos combinar términos radicales sólo
cuando tienen la misma expresión bajo el signo radical. Esto se parece mucho a la
combinación de términos semejantes en expresiones variables.
Ejemplo A
Simplificar las siguientes expresiones tanto como sea posible.
a.)
b.)
Es importante reducir los radicales a su forma más simple, a fin de asegurarse que
estamos combinando todos los posibles términos semejantes en la expresión. Por
ejemplo, la expresión
parece que no se puede simplificar más porque no
tiene términos semejantes. Sin embargo, cuando escribimos cada radical en su forma
más simple se obtiene
, y podemos combinar los términos de manera de
conseguir
.
Multiplicar expresiones radicales
Cuando multiplicamos expresiones radicales, utilizamos el "elevar un producto a la
potencia" regla:
. En este caso se aplica esta regla a la inversa.
Ejemplo C
Simplifica la expresión
Solución:
.
O bien, en la forma radical más simple:
Texto traducido de: www.ck12.org
www.guao.org
También haremos uso del hecho que:
.
Al multiplicar expresiones que tienen números en el exterior y en el interior del radical,
tratamos a los números fuera del signo radical y los números dentro del signo radical
separado. Por ejemplo,
.
Racionalizar el denominador
A menudo, cuando se trabaja con los radicales, nos encontramos con una expresión
radical en el denominador de una fracción. Lo tradicional es escribir nuestras fracciones
en una forma que no tengan radicales en el denominador, por lo que se utiliza un
proceso llamado racionalización del denominador para eliminarlas.
La racionalización es más fácil cuando hay sólo un radical y nada más en el
denominador, como en la fracción . Todo lo que tenemos que hacer es multiplicar el
numerador y el denominador por una expresión radical que haga que la expresión
dentro del radical en un cuadrado perfecto, cubo, o cualquier potencia. En el ejemplo
anterior, multiplicamos por
:
Raíces cúbicas y superior son un poco más difícil que las raíces cuadradas.
Ejemplo E
¿Cómo podemos racionalizar
Solución:
?
No podemos simplemente multiplicamos por el
, porque entonces el denominador
sería
. Para hacer el denominador un número entero, tenemos que multiplicar el
numerador y el denominador por
:
Más complicado aún es cuando la expresión en el denominador contiene más de un
plazo.
Ejemplo F
Texto traducido de: www.ck12.org
www.guao.org
Considere la posibilidad de la expresión
. No podemos multiplicar por
, porque
tendríamos que distribuir ese término y después el denominador sería
.
En su lugar, se multiplica por
. Esta es una buena opción ya que el
producto
es un producto de una suma y una diferencia, lo que
significa que es una diferencia de cuadrados. Los radicales se anulan entre sí cuando
llevamos
la
multiplicación
acabo,
y
el
denominador
se
vuelve
.
Cuando multiplicamos el numerador y el denominador
Consideremos ahora la expresión
, se obtiene:
.
Con el fin de eliminar las expresiones radicales en el denominador debemos multiplicar
por
.
Tenemos:
Vocabulario

Cuando multiplicamos expresiones radicales , usamos la regla de "elevar un producto a
la potencia":
.

Al multiplicar expresiones que tienen números en el exterior de un radical, tratamos a los
números fuera del radical y el número dentro del radical por separado:
Ejercicios
Simplificar las siguientes expresiones tanto como sea posible.
1.
2.
3.
Texto traducido de: www.ck12.org
www.guao.org
4.
5.
6.
Multiplica las siguientes expresiones.
7.
8.
9.
Racionalizar el denominador.
10.
11.
12.
13.
14.
15.
16.
17.
Texto traducido de: www.ck12.org
www.guao.org