Esquema de los contenidos del tema 15
Anuncio

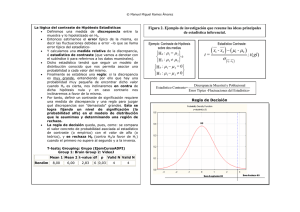
Análisis de Datos I Esquema del Tema 15 Tema 15: Contrastes de hipótesis sobre algunos parámetros 1. CONTRASTE DE HIPÓTESIS SOBRE LA MEDIA, Conocida Desconocida 2. CONTRASTE DE HIPÓTESIS SOBRE LA CORRELACIÓN, __________________ Bibliografía: Tema 15 (págs. 379-402) Ejercicios recomendados del libro: 1, 2, 3, 4, 5, 6, 7, 8 y 9. Carmen Ximénez 1 Análisis de Datos I Esquema del Tema 15 1. CONTRASTE DE HIPÓTESIS SOBRE LA MEDIA, Para contrastar hipótesis sobre el valor de una media vamos a distinguir dos casos: aquellos en los que se conoce la varianza poblacional, 2, y aquellos en los que no se conoce. Aunque el primer caso es muy infrecuente en la práctica, por razones didácticas se suele exponer en primer lugar. Contraste de hipótesis sobre la media, conocida σ El procedimiento consiste, como ya hemos visto en el tema anterior, en aplicar el esquema habitual con los siguientes pasos: 1) Hipótesis. Si se trata de un contraste bilateral, éstas serán de la forma, H0: µ = µ0 H1: µ ≠ µ0 2) Supuestos. - La población se distribuye N(µ; σ) o la muestra es suficientemente grande como para asumir la normalidad basándonos en el Teorema Central del Límite. - La media muestral se ha obtenido sobre una m.a.s. - Conocemos σ. 3) Estadístico de Contraste y su distribución bajo H0 verdadera. Z X 0 N ~ N(0; 1) 4) Regla de Decisión, basada en el nivel de significación (α) adoptado. Rechazar si Z ≥ 1-α/2z ó Z ≤ α/2z No rechazar si α/2z < Z < 1-α/2z 5) Decisión y Conclusión. Ejemplo 1. Supongamos que queremos contrastar la hipótesis de que la media poblacional en una determinada variable, X, es igual a 100, sabiendo que la varianza poblacional es igual a 64. Para ello extraemos una m.a.s. de 25 observaciones y calculamos su media aritmética en X, que resulta ser igual a 103. Establecemos un nivel de significación (α) de 0,05. 1) Hipótesis. H0: µ = 100 H1: µ ≠ 100 2) Supuestos. (Adviértase que en el problema no se especifica nada sobre la dirección de la diferencia entre 100 y la media poblacional real, en caso de ser falsa H0, por lo que se realiza un contraste bilateral) - La población se distribuye N(µ; 8) - Se trata de una m.a.s. - Conocemos σ 3) Estadístico de Contraste. En las condiciones indicadas, Z 4) Regla de decisión. 103 100 3,125 ; donde Z ~ N(0; 1) 8 25 Rechazar si Z ≥ 1,96 ó Z ≤ -1,96 No rechazar si -1,96 < Z < 1,96 5) Decisión y Conclusión. Como 3,125 > 1,96 rechazamos H0. Concluimos que la evidencia aconseja rechazar, según la regla de decisión adoptada, la hipótesis de que la media poblacional sea igual a 100. Carmen Ximénez 2 Análisis de Datos I Esquema del Tema 15 Contraste de hipótesis sobre la media, desconocida σ Con mucha frecuencia nos encontraremos en una situación como la anterior pero con la diferencia de que no conoceremos la varianza poblacional, σ2. Es decir, queremos contrastar si la media poblacional toma cierto valor y podemos asumir la normalidad de la población (o se trata de una muestra grande) y que la media se ha obtenido en una m.a.s. Si la única diferencia con el escenario anterior es que no conocemos la varianza poblacional (algo bastante razonable, dado que será raro que no conozcamos µ y en cambio conozcamos σ) entonces podemos recurrir a un estadístico similar al anterior, pero en el que en lugar de aparecer σ en el denominador aparece su estimador, SN o SN-1 (la desviación típica de la muestra), aunque en ambos casos la distribución es la misma: tN-1. El esquema, muy similar al del caso anterior, es el siguiente: 1) Hipótesis. H0: µ = µ0 H1: µ ≠ µ0 2) Supuestos. - La población se distribuye N(µ; σ) o la muestra es suficientemente grande como para asumir la normalidad basándonos en el TLC. - La media muestral se ha obtenido sobre una m.a.s. - Desconocemos σ. 3) Estadístico de Contraste. T X 0 S N 1 N ~ tN-1 o T X 0 SN N -1 ~ tN-1 4) Regla de Decisión. Rechazar si T ≥ 1-α/2tN-1 ó T ≤ α/2tN-1 No rechazar si α/2tN-1 < T < 1-α/2tN-1 5) Decisión y Conclusión. Ejemplo 2. Supongamos que queremos contrastar la hipótesis de que la media poblacional en una determinada variable, X, es igual a 80. Extraemos una m.a.s. de 81 observaciones y en ella obtenemos que su media es 75,8 y su varianza ( S N2 1 ) es igual a 236. Establecemos un nivel de significación (α) de 0,01. 1) Hipótesis. H0: µ = 80 H1: µ ≠ 80 2) Supuestos. - La población se distribuye N(µ; σ) - Se trata de una m.a.s. - Desconocemos σ. 3) Estadístico de Contraste. T X 0 S N 1 N 75,8 80 -2 , 461 ; donde T ~ t80 15, 36 81 4) Regla de decisión, con el nivel de significación adoptado (α = 0,01), Rechazar si T ≥ 2,639 ó T ≤ -2,639 No rechazar si -2,639 < T < 2,639 5) Decisión y Conclusión. Como el valor obtenido (-2,461) está entre ± 2,639 Mantenemos H0. La evidencia aconseja no rechazar, según la regla de decisión adoptada, la hipótesis de que la media poblacional sea igual a 80; la evidencia observada es compatible con ella. Carmen Ximénez 3 Análisis de Datos I Esquema del Tema 15 2. CONTRASTE DE HIPÓTESIS SOBRE LA CORRELACIÓN, El caso que exponemos aquí es única y exclusivamente aquel en el que queremos contrastar si la correlación de Pearson poblacional es 0. Los contrastes sobre cualquier otro valor exigen otros elementos que se expondrán en la asignatura de Análisis de Datos II. No obstante, el contraste del valor 0 es, con mucho, el más interesante y el que con mayor frecuencia se emplea. * Se trata de contrastar la independencia lineal entre dos variables; es decir, si la correlación poblacional (ρ) es igual a 0. Para ello necesitamos especificar un escenario en el que podamos definir un Estadístico de Contraste con una distribución conocida con la que establecer la regla de decisión. El escenario buscado es el que se resume en el siguiente esquema, en el que se llega a un Estadístico de Contraste que bajo hipótesis nula verdadera se distribuye según la t de Student con N – 2 grados de libertad (tN-2). 1) Hipótesis. H0: ρ = 0 H1: ρ ≠ 0 2) Supuestos. - Las dos variables a las que se refiere la correlación son normales. - La correlación muestral, rxy, se ha obtenido sobre una m.a.s. de pares de valores de X e Y. 3) Estadístico de Contraste. T rxy N - 2 1 rxy2 ~ tN-2 4) Regla de Decisión. Rechazar si T ≥ 1-α/2tN-2 ó T ≤ α/2tN-2 No rechazar si α/2tN-2 < T < 1-α/2tN-2 5) Decisión y Conclusión. Ejemplo 3. Supongamos que queremos contrastar si a nivel poblacional las variables X e Y son linealmente independientes. Extraemos una m.a.s. de 62 observaciones y en ella obtenemos una correlación de 0,28. Por estudios anteriores sabemos que podemos asumir que se trata de variables normales. Establecemos un nivel de significación (α) de 0,05. 1) Hipótesis. H0: ρ = 0 H1: ρ ≠ 0 2) Supuestos. - Ambas variables se distribuyen Normalmente en la población. - Se trata de una m.a.s. 3) Estadístico de Contraste. T rxy N - 2 1 rxy2 0 , 28 62 - 2 1 0 , 28 2 2 , 259 ; donde T ~ t60 4) Regla de Decisión. Rechazar si T ≥ 2,000 ó T ≤ -2,000 No rechazar si -2,000 < T < 2,000 5) Decisión y Conclusión. Como 2,259 no está entre ± 2,000, Rechazamos H0. La evidencia aconseja rechazar, según la regla de decisión adoptada, la hipótesis de que en la población estas variables sean linealmente independientes; la evidencia observada no es compatible con ella. Carmen Ximénez 4 Análisis de Datos I Esquema del Tema 15 Selección de una prueba de significación estadística 1. Diseño experimental empleado - Una, dos o más muestras - Independientes o relacionadas 2. Características de los datos - Escala de medida (cuantitativas vs. Cualitativas) - Distribución de la población (pruebas paramétricas vs. no paramétricas) - Tamaño de la muestra 3. Importancia del cumplimiento de los supuestos Tipos de contrastes: esquema CONTRASTES CON UNA MUESTRA Parámetro Media, Correlación, Supuestos y condiciones Estadístico y Distribución - Normalidad X 0 Z ~ N(0; 1) - Conocida N - m.a.s. - Normalidad X 0 T ~ tN-1 - Desconocida S N 1 N - m.a.s. - Normalidad rxy N - 2 ~ tN-2 - Hipótesis de independencia lineal, = 0 T 2 1 r - m.a.s. xy Proporción, Binomial Varianza, 2 Chi-cuadrado CONTRASTES CON DOS MUESTRAS Parámetro Igualdad de medias, 1 = 2 Supuestos y condiciones Muestras independientes - Asumiendo 21 = 22 - Asumiendo 21 22 Muestras relacionadas Igualdad de varianzas, 21 = 22 Muestras independientes Igualdad de proporciones, 1 = 2 Muestras independientes Carmen Ximénez Muestras relacionadas Muestras relacionadas Estadístico y Distribución t de Student t de Student F de Snedecor t de Student N(0;1) Binomial 5