Actividad III.31

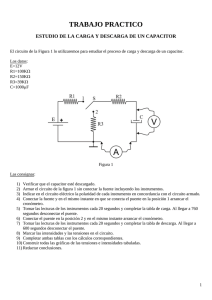
Actividad III.31 - Circuito RC
Objetivo
Estudio del proceso de carga y descarga de un capacitor. Determinación de las
constantes de tiempo características del circuito. Propiedades básicas de un circuito RC
(Resistencia y Capacitor). Respuesta transitoria y estacionaria. Respuesta de un circuito
RC a una señal cuadrada y senoidal. Determinación de la diferencia de fase de señales
senoidales.
Proyecto 1.- Carga y descarga de un capacitor usando un sistema de
adquisición de datos conectado a una PC
Equipamiento básico recomendado: Sistema de toma de datos con frecuencia de
muestreo de al menos 3 Hz, para ello puede utilizarse una tarjeta de toma de datos estándar o bien un multímetro conectado a una PC. Fuente de tensión continua o batería de
9 V. Resistencia y capacitores comerciales (C ≈ 10 µF y R ≈ 1 MΩ),
Usando el circuito descripto esquemáticamente en la Fig. 31.1, estudie los procesos de carga y descarga de un capacitor conectado a una resistencia (circuito RC). Se
sugiere el empleo de un sistema de adquisición de datos asociado a una PC. Para este
experimento, use un capacitor C y una resistencia R1 tales que su producto sea del orden
de 10 segundos. Elija para R2 un valor de aproximadamente el doble que R1. Conecte los
terminales del sistema de toma de datos en los bornes del capacitor C como muestra la
Fig. 31.1. También es útil disponer de un pulsador (interruptor). Asegúrese que la fuente
de tensión V0 tenga un valor inferior al máximo admisible por el sistema de toma de
datos; por lo general una batería de 9 V es adecuada para este estudio. Elija una frecuencia de muestreo (número de datos por segundo que el sistema de adquisición toma) del
orden de 100/(R1.C). Use el pulsador para cargar el capacitor. Antes de conectar, es
aconsejable una revisión cuidadosa del circuito.
!"
Represente gráficamente la dependencia de Vc (tensión en el capacitor) como
función del tiempo en el proceso de carga del capacitor a partir del momento
(t = 0) en que se conecta la fuente en el circuito. Obtenga el mejor ajuste de
la curva que describe la dependencia de Vc como función del tiempo.[1]
Con el objeto de linealizar la representación gráfica, construya un gráfico de
!"
dVc (t)/dt en función de Vc(t). A partir de estos gráficos, determine la constan-
te de tiempo τ1 característica de la carga del circuito R1-C.
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
1
Usando este mismo procedimiento, determine la constante de tiempo de tiem!"
po τ2 de la descarga del capacitor. Para esto, desconecte la fuente del circuito
después de que el capacitor se haya cargado (t >>τ1) y mantenga conectado el
capacitor con R2 . Mida Vc en función del tiempo a partir del momento en que
desconecta la fuente.
!"
Repita este análisis para otro conjunto de valores R1, R2 y C.
En cada caso
mida los valores de C, R1 y R2 usando un multímetro.
Usando sus datos y los de sus compañeros de clase, construya un gráfico de
!"
los valores de τ medidos experimentalmente en función de los valores del
producto R.C correspondientes.
!"¿Qué concluye de este estudio acerca de la dependencia del tiempo característico τ con respecto a los valores de R y C?
Proyecto 2.- Circuito RC − Respuesta estacionaria − Señal de excitación
cuadrada
Equipamiento básico recomendado: Osciloscopio de dos canales (de 10 MHz o más
rápido) o bien un sistema de toma de datos con frecuencia de muestreo mayor que 300
Hz. Generador de funciones con salida cuadrada. Resistencia y capacitores comerciales
(C ≈ 10 nF y R ≈ 500 kΩ),
Usando el circuito de la Fig. 31.2, estudie experimentalmente la variación de la
tensión en R y C, cuando se aplica una tensión cuadrada V(t). Un generador de funciones
con señal de salida cuadrada (de unos pocos volts de amplitud y una frecuencia del orden de los 30 Hz) alimenta el circuito y un osciloscopio (o sistema de adquisición) se
usa para monitorear las señales de tensión en cada elemento del circuito.
Nota: No todos los osciloscopios y las distintas salidas de los sistemas de adquisición de datos trabajan en modo diferencial, esto significa que sus entradas
de tierra (ground) son independientes. Verifique las especificaciones de su sistema. Si sus equipos trabajan en modo común, caso frecuente y que debe suponerse si no se está seguro, sólo puede medir las señales referidas a la tierra real
del circuito . Esto requiere que elija cuidadosamente este punto de circuito y
asegúrese que sea la misma tierra que la del generador de funciones. También
recuerde que tanto el osciloscopio como generador de funciones tienen resistencias internas. En general, los generadores de funciones pueden ser considerados como una fuente de tensión ideal, en serie con una resistencia Ri (Ri
≅50Ω).
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
2
Figura 31.1 Circuito para estudiar los procesos de carga y descarga de un
capacitor usando un sistema de toma de datos conectados a una PC
Para esta parte del experimento, pruebe con un capacitor C y una resistencia R
tales que R.C sea del orden de 20 ms. Conecte VR y Vc alternativamente a la entrada del
osciloscopio. Compare la forma de la señal de salida del generador de funciones con las
señales que se observan para VR y Vc.
Figura 31.2 Circuito para estudiar la respuesta de un circuito RC a una señal cuadrada usando un osciloscopio.
Se define la constante de tiempo τ del circuito como el tiempo que tardaría el
circuito en lograr su máximo (mínimo) valor de la carga si la variación en el tiempo
fuese una rampa de pendiente igual a la inicial (t=0). Un procedimiento para medir el
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
3
tiempo característico τ con el osciloscopio −en el caso de la descarga del capacitor−,
consiste en usar el procedimiento ilustrado en la Fig. 31.3.
Figura 31.3 Procedimiento gráfico par obtener la constante de tiempo usando un
osciloscopio. El ejemplo corresponde a la descarga del capacitor en un circuito
RC. Se traza la recta tangente en el origen (t = 0, cuando empieza la descarga) y el
valor de la abscisa donde la recta intercepta al eje horizontal nos da el valor de τ.
Estudie la dependencia de τ con R.
!"
Estudie la dependencia de τ con C.
!"
Represente gráficamente τ como función del producto R.C. ¿Qué conclu!"
siones obtiene de este estudio?
Nota: Recuerde que tanto el osciloscopio como la fuente de tensión tienen resistencias internas. En general los generadores de tensión puede ser considerados como una fuente de tensión ideal, en serie con una resistencia Ri (Ri ≅50Ω).
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
4
Proyecto 3.- Circuito RC − Respuesta estacionaria − Señal de excitación
senoidal
Equipamiento básico recomendado: Osciloscopio de dos canales (de 10 MHz o más
rápido) o bien un sistema de toma de datos con frecuencia de muestreo mayor que 300
Hz. Generador de funciones con salida senoidal. Resistencia y capacitores comerciales
(C≈ 100 nF y R ≈ 100 kΩ).
Respuesta estacionaria. Usando el circuito de la Fig. 31.4 con una fuente de tensión
senoidal, estudie la forma de Vc y VR como función de ω, la frecuencia angular de la
señal aplicada (ω= 2.π.f). Los valores de pico de la señal de entrada, en el capacitor y
la resistencia los denotamos con: Vi, VC y VR , respectivamente. La diferencias de fase
entre la tensión aplicada y la corriente la denotamos con φ. En el Apéndice G se presenta un método para determinar φ usando un osciloscopio.
Figura 31.4 Circuito para estudiar la respuesta de un circuito RC a una señal senoidal usando un osciloscopio
Represente gráficamente VR/Vi en función de ω.
!"
Represente gráficamente Vc/Vi en función de ω.
!"
Estudie la fase relativa, φ , de VR respecto de Vi. Represente en un gráfico φ
!"
en función de ω.
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
5
En todos estos casos, intente describir teóricamente sus resultados e incluya en los
gráficos anteriores los valores teóricos predichos por su modelo.
Bibliografía
1. D. Halliday, R. Resnick y J. Walker, Física para estudiantes de ciencias e ingeniería, 4ª ed. (Trad. de Fundamentals of Physics (John Wiley & Sons, Inc., New York,
1993).
2. E. M. Purcell, Berkeley physics course, Volumen 2, Electricidad y Magnetismo (Reverté, Barcelona, 1969).
3. P. Horowitz and W. Hill, The art of electronics, 2nd ed. (Cambridge University
Press, Cambridge, 1989).
Física re-Creativa – S.Gil y E. Rodríguez – Prentice Hall – Buenos Aires 2001
6