MST - LDC

CI2613: Algoritmos y Estructuras III
Árbol cobertor de peso mı́nimo
Blai Bonet
Universidad Simón Bolı́var, Caracas, Venezuela
Enero-Marzo 2015
c 2014 Blai Bonet
CI2613
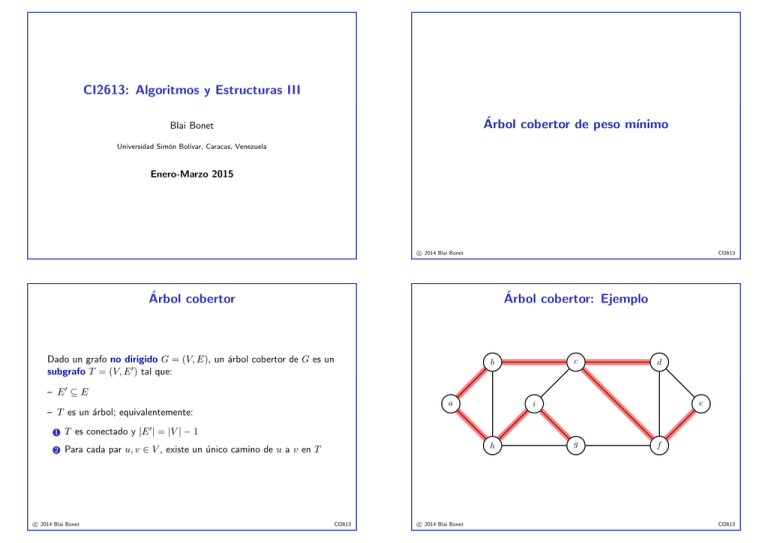
Árbol cobertor
Árbol cobertor: Ejemplo
Dado un grafo no dirigido G = (V, E), un árbol cobertor de G es un
subgrafo T = (V, E 0 ) tal que:
c
b
d
– E0 ⊆ E
a
e
i
– T es un árbol; equivalentemente:
1
T es conectado y |E 0 | = |V | − 1
2
Para cada par u, v ∈ V , existe un único camino de u a v en T
c 2014 Blai Bonet
h
CI2613
c 2014 Blai Bonet
g
f
CI2613
Árbol cobertor de peso mı́nimo
Árbol cobertor de peso mı́nimo: Ejemplo
Considere un grafo no dirigido G = (V, E) y pesos w(u, v) ∈ R para
cada arista (u, v) ∈ E
8
7
c
b
(V, E 0 )
Dado un árbol cobertor T =
de G:
P
– El peso de T es w(T ) = (u,v)∈E 0 w(u, v)
4
a
2
11
9
e
14
i
7
– Decimos que T es mı́nimo, de peso mı́nimo ó MST si
w(T ) ≤ w(T 0 ) para cualquier otro árbol cobertor T 0 de G
d
4
6
10
8
g
h
1
f
2
El árbol cobertor de mı́nimo peso es también llamado
Minimum(-weight) Spanning Tree (MST)
c 2014 Blai Bonet
CI2613
Algoritmos para el cálculo del MST
c 2014 Blai Bonet
CI2613
Método general para el cálculo de MST
Considere un grafo no dirigido G = (V, E) con pesos w : E → R
Veremos dos algoritmos greedy para el cálculo del MST:
La idea es construir un MST de forma iterativa:
– Algoritmo de Kruskal
– Inicialmente el pseudo-MST es vacı́o
– Algoritmo de Prim
– En cada paso se agrega o descarta una arista para el pseudo-MST
Ambos algoritmos pueden facilmente implementarse en tiempo
O(E log V ), pero el tiempo puede mejorarse para ambos algoritmos
– Se termina cuando el pseudo-MST es un árbol
El método garantiza el siguiente invariante al inicio de cada iteración:
Ambos algoritmos son instancias de un método general para MST
Si A son las aristas del pseudo-MST, existe un MST T = (V, E 0 )
tal que A ⊆ E 0
c 2014 Blai Bonet
CI2613
c 2014 Blai Bonet
CI2613
Aristas “seguras” y esquema general
Cortes de un grafo
Considere un grafo no dirigido G = (V, E) con pesos w : E → R
Considere una iteración del método general en donde ya hemos
calculado un conjunto A de aristas
– Un corte de G es una partición (S, V \ S) de sus vértices
Si (u, v) ∈ E es una arista tal que A0 = A ∪ {(u, v)} safisface el
invariante (i.e., existe un MST T = (V, E 0 ) con A0 ⊆ E 0 ), entonces
decimos que la arista (u, v) es segura para A
1
2
3
4
5
6
– Una arista (u, v) cruza el corte (S, V \ S) ssi u ∈ S y v ∈ V \ S
– Un corte (S, V \ S) respeta un conjunto de aristas A si ninguna
arista en A cruza el corte
generic-MST(G, w):
A = ∅
while A no es MST
Encontrar una arista (u,v) segura para A
A = A ∪ { (u,v) }
return A
– Una arista que cruza un corte (S, V \ S) es liviana si su peso es
mı́nimo entre todas las aristas que cruzan el corte
En general, una arista que satisface una propiedad ϕ es liviana si su
peso es mı́nimo entre todas las aristas que satisfacen ϕ
Para implementar el método tenemos que encontrar de forma
eficiente una arista segura para un conjunto dado A
c 2014 Blai Bonet
CI2613
c 2014 Blai Bonet
Encontrando aristas seguras
Cortes de un grafo: Ejemplo
8
7
c
b
4
a
Teorema
d
2
11
• un grafo G = (V, E) conectado y no dirigido con pesos w : E → R
e
14
• un subconjunto A ⊆ E contenido en un MST T = (V, E 0 ) de G
4
6
• un corte (S, V \ S) de G que respeta A
10
8
g
h
1
cruza el corte
c 2014 Blai Bonet
Considere:
9
i
7
CI2613
• una arista liviana (u, v) que cruza (S, V \ S)
f
2
Entonces, la arista (u, v) es segura para A
liviana
CI2613
c 2014 Blai Bonet
CI2613
Demostración del Teorema
•
•
•
•
Encontrando aristas seguras
un grafo G = (V, E) conectado y no dirigido con pesos w : E → R
un subconjunto A ⊆ E contenido en un MST T = (V, E 0 ) de G
un corte C = (S, V \ S) de G que respeta A
una arista liviana (u, v) que cruza C
Corolario
Considere:
• un grafo G = (V, E) conectado y no dirigido con pesos w : E → R
• un subconjunto A ⊆ E contenido en un MST T = (V, E 0 ) de G
Sea T = (V, E 0 ) un MST con A ⊆ E 0 . Debemos encontrar un MST
T 0 = (V, E 00 ) con A ∪ {(u, v)} ⊆ E 00 para mostrar que (u, v) es segura
• el grafo C = (VC , EC ) de componentes del bosque GA = (V, A)
• una arista liviana (u, v) que conecta componentes distintas en C
Suponga que A ∪ {(u, v)} * E 0 (en otro caso no hay nada que mostrar)
Entonces, la arista (u, v) es segura para A
Agreguemos (u, v) a T para formar un ciclo. El ciclo contiene una arista
(x, y) 6= (u, v) que cruza C (¿por qué?). Sea E 00 = (E ∪ {(u, v)}) \ {(x, y)}
0
00
Prueba: sean C1 y C2 las dos componentes de GA tal que u ∈ C1 y
v ∈ C2 . Considere el corte (C1 , V \ C1 ).
00
Veamos que T = (V, E ) es un MST y A ∪ {(u, v)} ⊆ E :
T 0 es conectado ya que existe camino x ; y y por lo tanto es árbol
2 w(T 0 ) = w(T ) + w(u, v) − w(x, y) ≤ w(T ) y por lo tanto T 0 es MST
3 (x, y) ∈
/ A porque C respeta A y (x, y) cruza C
4 Como A ⊆ E 0 , tenemos A ∪ {(u, v)} ⊆ E 00
Ninguna arista de A cruza el corte. Por otro lado, la arista (u, v) cruza el
corte y es liviana entre aquellas que lo cruza.
1
c 2014 Blai Bonet
Por el Teorema, la arista (u, v) es segura para A
CI2613
c 2014 Blai Bonet
Algoritmo de Kruskal
Algoritmo de Kruskal: Pseudocódigo
1
El algoritmo de Kruskal es una implementación del método general
2
3
4
El conjunto A de aristas define un bosque GA = (V, A)
MST-Kruskal(G, w):
% inicialización
A = ∅
foreach Vertice u: make-set(u)
5
6
7
Por el Corolario, cualquier arista liviana (u, v) que conecte dos
componentes de GA es segura para A y puede ser agregada sin violar
el invariante
8
9
10
11
12
c 2014 Blai Bonet
CI2613
CI2613
% algoritmo de Kruskal
Ordenar las aristas E de menor a mayor peso
foreach arista (u,v) en orden de peso
if find(u) != find(v)
A = A ∪ { (u,v) }
union(u,v)
return A
c 2014 Blai Bonet
CI2613
Algoritmo de Kruskal: Ejemplo
8
7
c
b
a
8
d
11
9
4
e
14
i
7
a
10
g
h
11
1
1
MST final
CI2613
c 2014 Blai Bonet
Algoritmo de Kruskal: Ejemplo
8
8
4
e
14
a
6
g
h
1
9
f
e
14
i
4
6
10
8
g
h
2
1
{a, b}, {c, f, g, h, i}, {d}, {e}
f
2
{a, b, c, d, e, f, g, h, i}
MST final
c 2014 Blai Bonet
11
7
10
d
2
4
8
7
c
b
9
i
7
Algoritmo de Kruskal: Ejemplo
d
2
11
CI2613
7
c
f
2
{a}, {b}, {c}, {d}, {e}, {f }, {g, h}, {i}
c 2014 Blai Bonet
a
g
h
MST final
4
10
f
{a}, {b}, {c}, {d}, {e}, {f }, {g}, {h}, {i}
e
14
4
6
8
2
b
9
i
7
8
d
2
4
6
7
c
b
2
4
Algoritmo de Kruskal: Ejemplo
MST final
CI2613
c 2014 Blai Bonet
CI2613
Algoritmo de Kruskal: Pseudocódigo
1
2
3
4
Análisis del algoritmo de Kruskal
MST-Kruskal(G, w):
% inicialización
A = ∅
foreach Vertice u: make-set(u)
1
El algoritmo es correcto por el Corolario
2
Tiempo para ordenar aristas: O(E log E)
3
Tiempo para todas las operaciones sobre la ED: O(E log∗ V )
4
Tiempo total:
5
6
7
8
9
10
11
12
% algoritmo de Kruskal
Ordenar las aristas E de menor a mayor peso
foreach arista (u,v) en orden de peso
if find(u) != find(v)
A = A ∪ { (u,v) }
union(u,v)
return A
O(E log E) + O(E log∗ V ) = O(E log V )
ya que E = O(V 2 ) y log∗ V = O(log V )
5
c 2014 Blai Bonet
CI2613
Si las aristas ya están ordenadas o se pueden ordenan en tiempo
lineal (e.g. con radix-sort si los pesos son enteros), el tiempo total
es O(E log∗ V ) que en la práctica es O(E)
c 2014 Blai Bonet
Algoritmo de Prim
CI2613
Algoritmo de Prim: Pseudocódigo
1
2
3
El algoritmo de Prim es una implementación del método general
4
5
6
El conjunto A define un único árbol que “crece” a partir de una raı́z
MST-Prim(G, w, r):
% inicialización
foreach Vertice u
key[u] = ∞
π[u] = null
key[r] = 0
7
8
Cada arista que se agrega a A es una arista liviana que conecta A
con algún vértice aislado
9
10
11
% cola de prioridad ordenada por min key[.]
PriorityQueue q
foreach Vertice u
q.insert(u)
12
13
Por el Teorema, dichas aristas son seguras para A
14
15
16
17
18
c 2014 Blai Bonet
CI2613
while q != ∅
u = q.extract-min()
foreach Vertice v in adyacentes[u]
if v ∈ q && w(u,v) < key[v]
key[v] = w(u,v) % involucra decresase-key
π[v] = u
c 2014 Blai Bonet
CI2613
Algoritmo de Prim: Ejemplo
8
7
b/∞
c/∞
4
a/0
8
d/∞
2
a/0
10
h/∞
g/∞
1
f /∞
8
CI2613
8
d/∞
2
7
6
a/0
g/∞
1
d/∞
d/7
2
9
i/∞
i/2
11
7
10
h/∞
h/8
c 2014 Blai Bonet
e/∞
14
c/∞
c/8
4
4
8
7
b/∞
b/4
9
i/∞
11
Algoritmo de Prim: Ejemplo
7
c/∞
c/8
f /∞
2
c 2014 Blai Bonet
Algoritmo de Prim: Ejemplo
a/0
g/∞
1
CI2613
4
10
h/∞
h/8
c 2014 Blai Bonet
e/∞
14
4
6
8
2
b/∞
b/4
9
i/∞
11
7
8
d/∞
2
4
6
c/∞
4
e/∞
14
7
7
b/∞
b/4
9
i/∞
11
Algoritmo de Prim: Ejemplo
6
8
f /∞
10
h/∞
h/7
2
g/∞
g/6
1
CI2613
c 2014 Blai Bonet
e/∞
14
4
ff/∞
/4
2
CI2613
Algoritmo de Prim: Ejemplo
8
7
b/∞
b/4
c/∞
c/8
4
a/0
8
d/∞
d/7
2
7
e/∞
e/10
14
a/0
10
g/∞
g/2
1
9
i/∞
i/2
11
ff/∞
/4
10
h/∞
h/1
g/∞
g/2
1
CI2613
e/∞
e/9
14
4
6
8
2
c 2014 Blai Bonet
d/∞
d/7
2
7
8
h/∞
h/1
c/∞
c/8
4
4
6
7
b/∞
b/4
9
i/∞
i/2
11
Algoritmo de Prim: Ejemplo
ff/∞
/4
2
c 2014 Blai Bonet
Invariantes en el algoritmo de Prim
CI2613
Análisis del algoritmo de Prim
Al inicio de cada iteración, el siguiente invariante se cumple:
1
El algoritmo es correcto por el Teorema
2
Tiempo en inicialización: O(V ) + O(V log V ) = O(V log V )
Invariante:
1
El conjunto de aristas es A = {(v, π[v]) : v ∈ V \ (Q ∪ {r})}
2
Los vértices en el pseudo-MST son aquellos que no están en la cola
3
Tiempo en ops. de cola: O(V log V ) + O(E log V ) = O(E log V )
3
Para todo vértice v: si π[v] 6= null,
4
Tiempo agregado para el lazo interno: O(E)
5
Tiempo total:
– key[v] < ∞
– Si v ∈ Q, key[v] es el peso de una arista liviana que conecta v
con el pseudo-MST
O(V log V ) + O(E log V ) + O(E) = O(E log V )
Por lo tanto, al inicio de cada iteración: si π[u] 6= null, entonces la
arista (u, π[u]) es una arista liviana que conecta el pseudo-MST con
un vértice aislado
c 2014 Blai Bonet
6
CI2613
Con un heap de Fibonacci, la operación decrease-key toma tiempo
O(1) amortizado y obtenemos un tiempo total O(E + V log V )
c 2014 Blai Bonet
CI2613
Resumen
• Queremos calcular un MST T para un grafo no dirigido y
conectado G = (V, E)
• Existe un método general iterativo basado en la idea de aristas
seguras y un invariante
• Dos implementaciones del método general:
– Algoritmo de Kruskal: mantiene un bosque de componentes
las cuales pueden crecer de forma independiente. Si las aristas
pueden ordenarse de forma eficiente, se puede implementar en
tiempo O(E log∗ V ) que en la práctica es O(E)
– Algoritmo de Prim: se crece una componente a partir de un
vértice raı́z. Una implementación con heap de Fibonacci se logra
en tiempo O(E + V log V )
c 2014 Blai Bonet
CI2613