MODELADO 1. Modelos El poder de un modelo matemático, radica

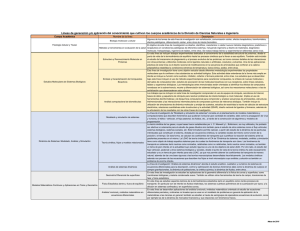
MODELADO
1. Modelos
El poder de un modelo matemático, radica en poder simular
situaciones hipotéticas, sujeto a estados que podrían ser
peligrosos en la realidad y se puede usar como base para
diseñar controladores.
2. Tipos de modelos
• Modelo nominal
Descripción aproximada de la planta que se usa para el
diseño del sistema de control.
• Modelo de calibración
Descripción más detallada de la planta.
• Modelo de error
Es la diferencia entre el modelo nominal y modelo de
calibración.
3. Construcción de modelos
• Modelo caja negra
Se postula una estructura de modelo específica y luego
se ajusta con ensayos.
• Modelo fenomenológico
Se usan leyes físicas para determinar las relaciones
entre las señales del sistema.
• Modelo mixto
En la práctica es común combinar los dos métodos.
4. Estructura de modelos
• Con ecuaciones diferenciales (tiempo continuo)
• Con ecuaciones de diferencia (tiempo discreto)
• Combinación de los anteriores
5. Modelo en el espacio de estado
En el modelado se usan variables de estado. Son un
conjunto de variables internas que permiten determinar
las salidas de una planta en función de ellas.
• Caso general
dx(t)
= f(x(t),u(t), t)
dt
y(t) = g(x(t),u(t), t)
x(t) vector de estado
• Modelos en el espacio de estado lineal invariante en el
tiempo
dx(t)
= Ax(t) + Bu(t)
dt
y(t) = Cx(t) + Du(t)
donde A, B, C y D son matrices constantes
• Solución de modelos en espacio de estado
x(t) = e
donde
A(t−to )
t
xo + ∫ e A(t−τ)Bu( τ) dτ
to
∞
e At = I + ∑ 1 A i t i
i=1 i!
la salida es :
t
A(t−to )
y(t) = Ce
xo + C ∫ e A(t−τ)Bu( τ) dτ + Du(t)
to
Los vectores x(t) como y(t) consisten de dos términos.
Uno debido a la condición inicial xo y el otro a la entrada u(t).
6. Modelos con ecuaciones diferenciales
La forma general es:
 n

d y(t)
dm−1u(t)

f
,......., y(t),
,....., u(t) = 0
n
−
m
1
dt
dt


donde f[] es una función nolineal.
7. Errores de modelado
Sean:
y = g(u) la planta verdadera
yo= go(u) el modelo nominal
donde g y go son transformaciones
• Modelo aditivo (AME)
Se define por una transformación gЄ:
y = yo + gЄ(u)
• Modelo multiplicativo (MME)
Se define por una transformación g∆:
y = go(u + g∆(u))
Tiene escalamiento relativo al tamaño del modelo
nominal.