Diapositiva 1

CRISTALOGRAFIA
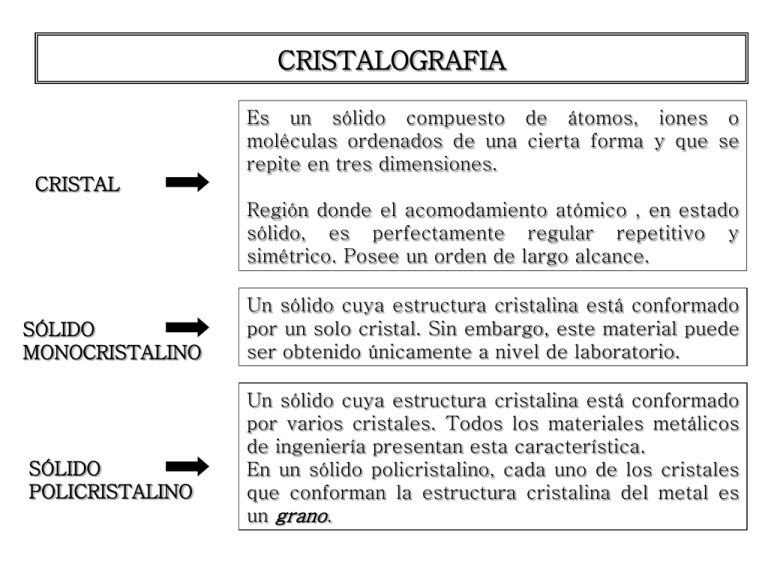
Es un sólido compuesto de átomos, iones o
moléculas ordenados de una cierta forma y que se
repite en tres dimensiones.
CRISTAL
Región donde el acomodamiento atómico , en estado
sólido, es perfectamente regular repetitivo y
simétrico. Posee un orden de largo alcance.
SÓLIDO
MONOCRISTALINO
SÓLIDO
POLICRISTALINO
Un sólido cuya estructura cristalina está conformado
por un solo cristal. Sin embargo, este material puede
ser obtenido únicamente a nivel de laboratorio.
Un sólido cuya estructura cristalina está conformado
por varios cristales. Todos los materiales metálicos
de ingeniería presentan esta característica.
En un sólido policristalino, cada uno de los cristales
que conforman la estructura cristalina del metal es
un grano.
CRISTALOGRAFIA
ESTRUCTURA
CRISTALINA
RED
ESPACIAL
Modelo regular de tres dimensiones de átomos o iones
en el espacio.
Se denomina a la red tridimensional de líneas
imaginarias que conecta los átomos. También puede
ser descrita como una matriz tridimensional de puntos
en los que cada uno tiene idénticos alrededores.
CELDA
UNITARIA
La celda unitaria es la unidad más
pequeña que tiene la simetría total.
La celda unitaria específica para
cada metal está definida por sus
parámetros. El tamaño y la forma de
la celda unidad puede describirse
por los vectores reticulares a,b,c
que se originan a partir de un
vértice de la celda unidad y los
ángulos  (entre b y c),  (entre a y
c) y  (entre a y b).
PRINCIPALES ESTRUCTURAS CRISTALINAS
SISTEMAS CRISTALINOS
Y REDES DE BRAVAIS
Catorce celdillas de unidad
estándar describen todas las
redes posibles.
BASICAS:
1)Simple
2)Centrada en el cuerpo
3)Centrada en las caras
4)Centrada en la base
SISTEMAS CRISTALINOS
Celdillas unidad de las
principales
estructuras
cristalinas metálicas.
(a)Cúbica centrada en el
cuerpo BCC
(b)Cúbica centrada en las
caras FCC
(c)Hexagonal compacta HCP
Ejemplo: Hierro Cúbico Centrado en el Cuerpo
Arista: 0.287 x 10 -9 m o 0.287 nm
Si las celdillas unidad del hierro puro estuvieran alineadas arista
con arista en un (1) mm.
1 celda unidad
6
1 mm x

3
,
48
x
10
celdas unidad
6
0.287 nm x 10 mm / nm
CELDA BCC
Celdillas unidad BCC
(a) Posiciones atómicas
(b) De esferas rígidas
(c) Celdilla unidad aislada
Los átomos en la celda
BCC contactan a lo largo
de las diagonales del
cubo. Si a es la longitud
del lado del cubo:
3 a 4R
a
4
R
3
Si los átomos se representan
como esferas, el átomo del
centro toca a cada átomo de las
esquinas, pero estos no se tocan
entre sí. Cada átomo de las
esquinas lo comparten ocho
cubos adyacentes y el átomo del
centro no puede compartirlo
ningún otro cubo. Por lo tanto, la
celda unitaria de la estructura
B.C.C. contiene 2 átomos.
8 átomos en las esquinas * 1/8 =
1 átomos
+ 1 átomos central = 2 átomos.
CELDA FCC
Celdillas unidad FCC
(a) Posiciones atómicas
(b) De esferas rígidas
(c) Celdilla unidad aislada
Los átomos en la celda
BCC contactan a lo largo
de las diagonales de las
caras. Si a es la longitud
del lado del cubo:
2 a 4R
a
4
R
2
Cada átomo de las esquinas lo
comparten ocho cubos adyacentes y
cada átomo de las caras es compartido
solo por un cubo adyacente, la celda
unitaria en total tiene 4 átomos.
8 átomos de cada esquina * 1/8 = 1
átomo
6 átomos centrados en la cara * ½ = 3
átomos
CELDA HCP
Celdillas unidad HCP
(a) Posiciones atómicas
(b) De esferas rígidas
(c) Celdilla unidad aislada
La celda unidad H.C.P. , tiene un equivalente de seis (6) átomos por celda unidad.
Tres átomos forma un triángulo en la capa intermedia.
Existen 6 * 1/6 de átomos en las capas de arriba y abajo, haciendo un equivalente
de 2 átomos más ( 2 * 6 * 1/6 = 2)
Finalmente, hay dos mitades de átomos en el centro de ambas capas superior e
inferior, haciendo el equivalente de un átomo más.
Por lo tanto , el número de átomos en la estructura H.C.P. es 3 + 2 + 1 = 6.
La relación de la altura c del prisma hexagonal de la estructura cristalina H.C.P. al
lado de la base a , se llama relación c/a.
CELDA HCP
La relación c/a para una estructura
cristalina H.C.P. ideal consistente en
esferas uniformes tan próximas como
sea posible es 1,633.
En tablas se muestran algunos
metales H.C.P. importantes y sus
relaciones c/a. Ejemplos es que el
Cadmio y Cinc, tienen una relación
c/a más alta que la ideal, lo que nos
indica que los átomos en estas
estructuras
están
ligeramente
elongados a lo largo del eje c en la
celda unidad H.C.P. Los metales
magnesio, circonio, titanio y berilio
tienen relaciones c/a menores que la
ideal, por lo tanto, en estos metales
los
átomos
están
ligeramente
comprimidos a lo largo de c.
CRISTALIZACION DE METALES
POSICIONES EN LA RED CUBICA
Una posición determinada en una celda
unidad
dada
es
estructuralmente
equivalente a la misma posición en
cualquier otra celda unitaria de la misma
estructura.
Posiciones del retículo expresadas
como fracciones (o múltiplos) de las
dimensiones de la celda unitaria.
Estas posiciones equivalentes están
conectadas mediante traslaciones de la
red, que consisten de múltiplos enteros
de las constantes de red a lo largo de las
direcciones
paralelas
a
los
ejes
cristalográficos.
DIRECCIONES EN LA RED CUBICA
Notación para las direcciones
reticulares
Una dirección en una celda unidad
cúbica está indicada por un vector
dibujado desde el origen a un punto
en la celda unidad a través de la
superficie de la celda unidad.
Para determinar las direcciones en el
sistema Cúbico se debe considerar:
1.- El origen de los ejes se escogen a
conveniencia.
2.- Los ejes tienen un valor de uno.
3.- Las coordenadas de una dirección
dentro del cristal se denotan
[h k
l, siendo h, k y l las proyecciones
sobre
los
ejes
a,
b
y
c
respectivamente.
4.- Las familias de direcciones se
denota <h k l>, siendo una familia de
direcciones la permutación de las
coordenadas de una dirección dada
Notación empleada para describir las
direcciones
reticulares.
Las
direcciones
se
cierran
entre
corchetes, lo que constituye la
designación
estándar
de
las
direcciones de la red.
DIRECCIONES EN LA RED CUBICA
Vectores dirección en celdillas unidad cúbicas
PLANOS EN LA RED CUBICA
Planos reticulares o los planos de la red
cristalográfica
(Índices de Miller)
Las recíprocas de las intersecciones de un
plano del cristal con los ejes X,Y,Z de una
celda unidad se llaman Índices de Miller de
un plano.
Para determinarlos se debe considerar:
1.- El origen de los ejes se escogen a
conveniencia, pero se debe tener presente
que el origen no puede estar contenido en el
plano.
2.- Por conveniencia, generalmente los ejes
tienen un valor de uno.
3.- Las coordenadas de un plano dentro del
cristal se denotan (h k l), siendo h, k y l el
inverso de los cortes del plano con los ejes
cristalinos a, b y c, es decir:
a = 1/h ; b = 1/k y
c = 1/l.
4.- Las familias de planos se denota {h k l},
siendo una familia de planos la permutación
de las coordenadas de un plano dado.
DIRECCIONES Y PLANOS EN LA RED CUBICA
Direcciones en celdillas unidad cúbicas
Índices de Miller de algunos planos cristalinos cúbicos
importantes
FAMILIA DE DIRECCIONES Y PLANOS EN EL
SISTEMA CUBICO
La familia de direcciones <111>
representa todas las diagonales del
cuerpo en el caso de celdas unidad
adyacentes al sistema cúbico.
La
familia
de
planos
{100}
representa todas las caras de la
celda unidad en el sistema cubico
INDICES EN LA CELDA HCP
Las superficies cristalinas en celdillas unidad
HCP pueden ser identificadas utilizando
cuatro índices en vez de tres.
Los índices para los planos cristalinos HCP,
llamados índices de Miller-Bravais, son
designados por las letras h,k,i,l, encerrados
entre paréntesis (hkil).
Existen tres ejes básicos a1, a2 y a3 que
forman 120º entre sí. El cuarto eje (c) es
vertical y está localizado en el centro de la
celda unidad.
La unidad a de medida a lo largo de los ejes
a1, a2 y a3 es la distancia entre los
átomos a lo largo de estos tres ejes. La
unidad medida a lo largo del eje c es la
altura de la celdilla unidad.
Los recíprocos de las intersecciones que un
plano cristalino determina con los ejes a1 , a2
y a3 , proporcionan los índices h,k e i
mientras el recíproco de la intersección con
el eje c da el índice l.
La unidad medida en c es la altura de la celda
HCP.
INDICES EN LA CELDA HCP
ESPACIAMIENTO INTERPLANAR Y ANGULO ENTRE
PLANOS
dh k l 
a
h 2  k 2  l2
En
el
sistema
cúbico,
el
espaciamiento Interplanar entre
dos planos paralelos y cercanos
con los mismos índices de Miller
se designa como d h k l, donde d
h, k y l son los índices de Miller
de los Planos y a es el parámetro
reticular .
Cos 
h
2
1
h1h2  k1k 2  l1l2
2
2

2
2
 k1  l1 h2  k 2  l2
2

En el sistema Cúbico, el ángulo 
entre los planos (h1 k1 l1) y (h2 k2 l2)
puede determinarse mediante la
fórmula:
POLIMORFISMO
POLIMORFISMO, ( ALOTROPIA):
Capacidad que tiene un material de presentar
más de un tipo de estructura cristalina a
diferentes
condiciones
de
presión,
temperatura y grado de deformación. La
transformación de una estructura cristalina a
otra se denomina entonces: transformación
alotrópica. Y al material que la presenta se le
llama polimórfico
o
alotrópico. Tales
transformaciones
ocurren
sin
producir
cambios en la composición química.
CAUSAS DEL FENOMENO:
En ciertos rangos de temperatura, un arreglo
atómico es más estable que otro para un
determinado material.
EJEMPLOS:
Hierro (Fe), Cobalto (Co), Estaño (Sn),
Manganeso (Mn), Cromo (Cr) y Titanio (Ti).
Cuando el hierro cristaliza a 2800ºF es B.C.C.
(Fe ), a 2554ºF la estructura cambia a
F.C.C.
(Fe ) y a 1670ºF vuelve a
transformarse en B.C.C. (Fe ).
DENSIDAD VOLUMETRICA ,PLANAR Y LINEAL
masa / celdillaunidad
Densidad volumetrica del metal    
volumen / celdillaunidad
núm. equiv. de atomos cuyos centros
están int er sectados por el área seleccionada
Densidad atomica planar   
área seleccionada
Densidad atomica lineal    
núm. de átomos diametralmente int er sectados
por una longitudde una líneade dirección dada
longitudde la línea seleccionada