1er Exámen Parcial 2006-2 - División de Ciencias Básicas

FACULTAD DE INGENIERÍA
1ER. EXAMEN PARCIAL DE TERMODINÁMICA
DIVISIÓN DE CIENCIAS BÁSICAS
SÁBADO 8.4.2006., 13:00 (h), SEM 2006-2
DEPARTAMENTO DE FÍSICA GENERAL Y QUÍMICA
COORDINACIÓN DE TERMODINÁMICA
EVANGELISTA TORRICELLI (1608-1647)
Instrucciones: lea cuidadosamente los problemas que se ofrecen y resuelva cualesquiera cuatro en dos
horas. La consulta de cualquier documento propio es decisión del profesor.
1.- Un motor eléctrico operando en estado estable requiere una entrada de potencia eléctrica de 1055 (W).
La flecha del motor desarrolla un par de 19.53 (Nm) con una velocidad angular de 500 rpm. La superficie
del motor transfiere calor al ambiente según la ley de enfriamiento de Newton, Q = hA(Tb - T∞), donde h
= coeficiente de transferencia de calor = 3.8 (kW/m2K), A=área superficial del motor = 2600 (cm2), T∞ =
temperatura del ambiente = 25(ºC) y Tb=temperatura superficial del motor. Calcule Tb.
2.- Se utiliza un calefactor de 1(kW) para calentar el aire de un recinto cónico de radio igual a 3(m) y de
altura igual a 5(m) desde una temperatura ambiente de 25(ºC) hasta la temperatura normal del cuerpo
humano (37(ºC)). Despreciando las pérdidas, ¿Cuánto tiempo tomará para calentar el recinto?
Considere:
caire = 0.7291(J/g ∆K)
ρaire = 1.0(kg/ m3)
Dé su respuesta en minutos.
3.- Un dispositivo mecánico lleva incorporado un resorte que tiene una constante de fuerza de 2 x 106
(N/m) unido a una leva que lo comprime y expande alternativamente a una distancia de 1(cm) del
equilibrio. El resorte está en contacto con una masa de metal aislada térmicamente y de capacidad
calorífica de 4.2(kJ/K). Si la temperatura inicial del metal es de 20(º C). ¿Cuál será la temperatura del
metal después de 1000 oscilaciones? Cada oscilación sucede en 1(s).
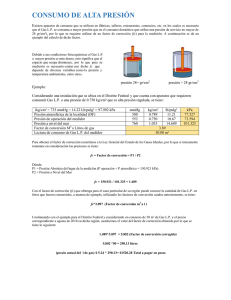
4.- Un tubo capilar de 1(m) de largo está cerrado por ambos lados. El tubo contiene 2 columnas de aire
separadas por una columna de mercurio de 0.2(m) de largo. Con el tubo en posición horizontal ambas
columnas de aire son de 0.4(m) de largo, pero con el tubo en posición vertical la columna superior de aire
es de 0.5(m) de largo y la inferior es de 0.3(m) de largo. ¿Cuál es la presión en el tubo capilar cuando el
tubo está en posición horizontal? Suponga que el aire sigue la relación P*V = C, donde C es una
constante. Considere ρHg=13590(kg/m3) y g=9.78(m/s2).
5.-Un depósito sin fondo como se muestra en la figura, cuya masa es de 5(kg) y 50(cm) de diámetro
inferior, se localiza sobre una superficie plana que cierra al depósito herméticamente. Se le agrega aceite
para máquinas (δ = 0.91) de tal suerte que éste ocasiona que se separe el depósito de la superficie. El
diámetro del cilindro inferior es 5 veces más grande que el superior. Calcule la columna del fluido que
ocasionará ese efecto.
Sin fondo
6.- En un tanque abierto a la atmósfera de la CU, de 3(m) de radio de la base, de 1(m) de radio superior y
de 2(m) de altura (un cono truncado), hay que meter un líquido (δ = 1.65) para que en el fondo del tanque
se alcancen 90(kPa) absolutos. Si para el agua puede tomarse 998(kg/m3) y para la CU se tienen 20(ºC),
9.78(m/s2) y 78(kPa), calcule el volumen necesario.
Resolución del primer examen colegiado de Termodinámica. Semestre 2006-2
Sábado 8 de abril de 2006. 13:00 (h)
EVANGELISTA TORRICELLI (1608-1647)
1.- {W}elect = 1055 (W), τ = 19.53 (Nm), ω = 500 rpm, h = 3.8 (W/m2K), A = 2600 (cm2),
T∞=25(ºC); {Q}+ {W}elect +{W}flecha=0, Tb = T∞ +({W}elect – τω)/( hA); Tb = 57.8 (ºC)
2.- {Q} = 1.0 (kW), V = (π r2h)/3, Ti = 25 (ºC), Tf = 37 (ºC), r =3(m), h= 5(m),
caire=0.7291(J/g∆K), ρaire = 1.0 (kg/m3); t = (ρaire π r2 h caire (Tf – Ti))/(3{Q}); t = 6.8716 (min).
3.- k = 2 x 106 (N/m), x= 0.01 (m), C = 4.2 x 103 (J/K), Ti =20 (ºC), N=1000 oscilaciones; Tf =
({W}/C) +Ti; Tf = 67.619 (ºC).
4.- lHg = 0.2 (m), linicial= 0.4 (m), lsup= 0.5 (m), linf=0.3 (m), ρHg=13590 (kg/m3), g=9.78 (m/s2);
Po= (ρHg g lHg)/linicial((1/linf) – (1/lsup)); Po=49.841 (kPa).
5.- m=5(kg), Dinf =0.5 (m), δaceite=0.91, Dinf = 5 Dsup; z = m/(δaceite ρagua A), A= (π(Dinf2 – Dsup2)/4;
z = 2.9149 (cm).
6.- R=3(m), r=1(m), zcono=2 (m), δ =1.65, Pfondo= 90 (kPa), ρagua=998 (kg/m3), Tamb= 20 (ºC),
g=9.78 (m/s2), Pamb=78 (kPa); zf= (Pfongo – Pamb)/ (δρagua g)= 0.74512 (m), Vtotal= Vfluido – Vsup,
Vtotal = (πR2(zcono+ lsup))/3, Vsup= (πrf2L)/3; Vfluido = 16.26 (m3)
DANIEL BERNOULLI (1700-1782)
a .- T∞ = 20 (ºC); Tb = 52.8 (ºC).
b.- {Q}= 1.5 (kW); t = 4.58 (min).
c.- k = 1.5 x 106 (N/m); Tf = 55.71 (ºC).
ch.- Po =49.841 (kPa).
d.- m= 7 (kg); z = 4.08 (cm).
e.- Vfluido = 16.26 (m3).