Bob produce películas de DVD para su venta, lo que requiere sólo
Anuncio

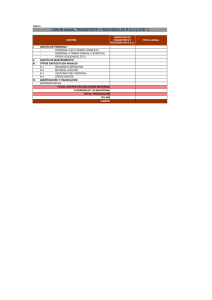
1.- Bob produce películas de DVD para su venta, lo que requiere sólo disponer
de un local y una máquina que permita copiar la película original en el soporte
DVD. Bob alquila un local por 300 euros al mes y alquila también una máquina
por 200 euros al mes. Ambos son sus costes fijos. Supongamos que la
producción de DVD es una industria perfectamente competitiva. Su coste
variable se proporciona en la tabla adjunta.
Q
0
10
20
30
40
50
60
70
80
90
100
CV
0
50
80
90
140
200
330
490
720
990
1500
Calcule CMeV de Bob, CMeT y el CMa para cada volumen de producción.
a. Si la empresa maximiza beneficios, ¿cuál es el precio de beneficio nulo
de Bob? ¿Cuál es su precio de cierre?
b. Suponga que el precio de DVD es de 2 euros. ¿Qué debería hacer Bob
en el corto plazo?
c. Suponga que el precio del DVD es de 7 euros. ¿Cuál es la cantidad de
DVDs maximizadora del beneficio que debería producir Bob?
¿Producirá o cerrará en el corto plazo? Dibuje la curva de CMa de
Bob.
d. ¿Para qué rango de precios Bob no producirá ningún DVD en el
corto plazo?
e. Dibuje la curva de oferta individual de Bob.
a)
b) Sabiendo que el beneficio nulo es aquel cuyo precio es igual al mínimo
del coste medio total (CmT), según la tabla anterior dicho precio será:
P=13.83.
Por otro lado el “precio de cierre” a corto plazo coincide con el mínimo del
coste medio variable (Cvme), en nuestro caso p=3.
c) En este caso con p=2, además de tener pérdidas se encuentra por debajo
del precio de cierre. Por lo tanto, debería cerrar.
d) Si p=7, q*=Ima=Cma=50, Por lo tanto, tiene pérdidas pero aún así no
debe cerrar a corto plazo.
e)
f)
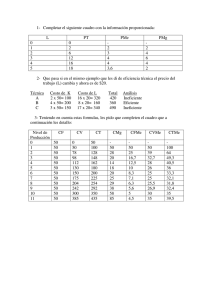
2. La función de costes de un empresa competitiva responde a la siguiente especificación
C=100+2q+q2. Determine y represente gráficamente:
1) Las funciones costes medios totales, de costes medios variables y costes marginales.
2) La función de oferta de la empresa.
3) Señale en la gráfica el umbral de beneficios (beneficio = 0) y calcule el precio y
cantidad correspondientes
4)
Señale en la gráfica el umbral de producción (mínimo de la explotación), calcule el
precio y cantidad correspondientes y delimite el intervalo de validez de la función de
oferta
5) ¿Si el precio fuese 10, cuál sería la producción y beneficio (o pérdida) de la empresa ?
6) ¿Si el precio fuese 24, cuál sería la producción y beneficio (o pérdida) de la empresa ?
Solución
1)
2)
3)
4)
5)
6)
Cmd,t=100/q+2+q; Cmd,v=2+q; Cmq=2+2q;
P= Cmq=2+2q→q=(p-2)/2 para todo p>minCmd,v=2
Umbral de beneficios: min Cmd,t o Cmd,t=100/q+2+q=2+2q= Cmg →100/q=q →
qub=10→ pub=2+2q=22.
Umbral de producción: min Cmd,v o Cmd,v=2+q=2+2q= Cmg → qup=0→ pup=2. La
función de oferta q=(p-2)/2 queda delimitada para todo p≥2.
P=10 →q=(p-2)/2=4; Π=pq-C(q)=40-(100+2*4+42)=-86< pérdidas, 86<100=CF, la
empresa produce a pérdidas porque absorbe una fracción del coste fijo (14%).
Comprobación p4>pup=2 →pérdida menor que el coste fijo.
P=24 →q=(p-2)/2=11; Π=pq-C(q)=264-(100+2*11+112)=21>0, la empresa obtiene
beneficios extraordinarios, gana por encima de la rentabilidad social media.
Comprobación p=24>pub=22 → Π>0, ganancias extraordinarias.
Notación: Cmd,t coste medio total; Cmd,v= coste medio variable; Cmg=coste marginal; CF
coste fijo. Subíndices up y ub para umbral de producción y umbral de beneficios.
3.- Los laboratorios farmacéuticos CANARIPHARMA han creado un nuevo
medicamento para la gripe denominado GRIPISÍN®, que es capaz de curar esta
enfermedad en 24 horas. El Ministerio de Sanidad ha concedido la patente para
vender en exclusiva este medicamento durante cinco años a Canaripharma. Se ha
estimado que la fabricación de CADA frasco de Gripisín® costará 10+0,02Q (siendo Q
el número de frascos del medicamento fabricados anualmente).
a) Si la demanda anual de Gripisín® responde a la función p=150-0,05Q, calcule el
precio al que se venderá cada frasco de Gripisín®. Represente gráficamente la
situación.
b) El Ministerio de Sanidad impone a Canaripharma un canon anual de cuantía fija por
seguir operando en régimen de monopolio. Tras el pago de dicho canon, Canaripharma
contabiliza unas pérdidas de 30.000 u.m. Según esta cifra, ¿a cuánto ha ascendido el
canon? Complete el gráfico anterior con este dato, señalando el área correspondiente
al coste pagado en concepto de canon.
c) Finalizado el plazo de cinco años dado a Canaripharma para explotar
monopolísticamente este mercado, y dado que Canaripharma no tuvo la demanda que
esperaba, se decide adoptar la siguiente medida. El Ministerio de Sanidad resuelve que
Canaripharma pueda seguir produciendo en exclusiva durante el sexto año, pero solo
se le permite fijar un precio que maximice sus ingresos (no beneficios). Calcule el
nuevo precio y la cantidad producida y sitúelos en el gráfico.
d) Si el Ministerio exigiese un canon de 70.000 u.m, (permitiéndole producir la
cantidad que quisiese) ¿Qué haría el monopolista en el corto plazo y en el largo plazo?
Justifique su respuesta.
SOLUCION
Funciones de Costes
Como CVMe= 10+0.02Q
CVT=CVMe*Q = 10Q+ 0.02Q2
Cma = dCVT/dQ = 10+0.04Q
a) Si la Demanda es p=150-0.05Q
IT = Ime*Q = 150Q-0.05Q2
Ima= dIT/dQ = 150-0.1Q
Como Canaripharma es un monopolista, producirá donde maximice el beneficio:
1) Ima=CMa
150-0.1Q = 10+0.04Q; por tanto, Q = 1000
y el precio se calcula sustituyendo en la función de demanda:
p= 150-0.05(1000) = 100
2) dCMa>dIMa
0.04>-0.1 (Luego existe un máximo en la función de beneficios).
3) p≥CVMe (o IT≥CVT)
cuando Q=1000, CVMe=10+0.02(1000) = 30
100>30, luego la empresa PRODUCE en el corto plazo al cubrir el CVT.
Luego Canaripharma producirá la cantidad Q=1000 y fijará el precio p=100.
Gráficamente:
U.m.
150
CMa
100
CVMe
30
IMa
10
1000
1500
D
3000
Q
b) El Canon establecido actúa como un coste fijo para Canaripharma.
Si las pérdidas son 30.000, quiere decir que IT-CT = -30.000
Como el monopolista produce Q=1000 al precio p=100, tenemos que:
1001.000 - (CFT + 10·1.000 + 0.02·1.0002) = -30.000
100.000 - (CFT + 30.000) = -30.000
Despejando CFT (sería el canon), tenemos que:
Canon = 100.000
La función de coste total quedaría:
CT= 100.000+10Q+0.02Q2
con lo que CTMe= 100.000/Q + 10 + 0.02Q
Para el volumen de producción 1.000, CTMe= 130, y CFMe= 100
Gráficamente, el área del canon es el CFT=100.000, con lo que completando el gráfico
anterior:
CTMe
U.m.
150
CANON
CMa
130
CFMe=100
{
100
CVMe
30
D
IMa
10
1000
1500
3000
Q
c) se maximiza el ingreso total donde el Ingreso Marginal es igual a cero.
Ima=0; 150-0.1Q=0, con lo que: Q=1.500
y si Q=1.500, el precio sería: p=150-0.05·1500 = 75. Gráficamente:
CTMe
U.m.
CANON
Aquí se Maximizan ingresos
150
CMa
130
100
75
CVMe
30
IMa
10
1000
1500
D
3000
Q
d) Si el canon exigido es 70.000, (CT=70.000+10Q+0.02Q2), la empresa seguiría
produciendo donde maximizase el beneficio (Q=1000, p=100). Sin embargo, en este
caso, el Coste Total Medio sería 100 (igual que el precio), con lo que IT=CT, es decir, la
empresa obtendría beneficios normales. Gráficamente:
U.m.
CTMe
150
CMa
130
100
CVMe
30
IMa
10
1000
1500
D
3000
Q
A corto plazo la empresa produciría ya que al obtener beneficios normales está
cubriendo sus costes variables (además de los fijos) (por lo tanto p>CVMe)
En el largo plazo, el monopolista en principio seguiría produciendo en esta situación,
con lo que seguiría obteniendo beneficios normales. Sin embargo, los beneficios
normales parecen ser un beneficio muy pobre para una empresa que intenta explotar
una situación de monopolio. Es posible que la empresa intentase obtener mayores
beneficios mediante un redimensionamiento de su planta para (disminuyendo costes)
obtener beneficios extraordinarios.