1 cf 0.4 1.74 ln Re cf p u 24 D Re D um 12 µ fM 64 Re 1 fM 2
Anuncio

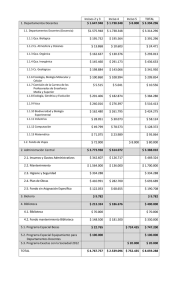
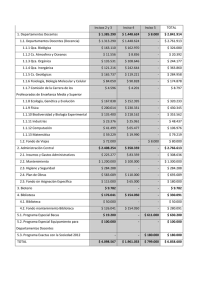
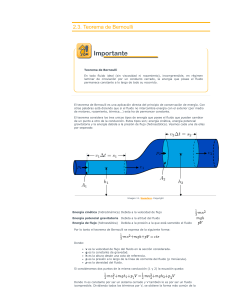
UNIVERSIDAD TECNOLÓGICA NACIONAL - FACULTAD REGIONAL ROSARIO Departamento de Ingeniería Química INTEGRACIÓN IV Año 2000 Trabajo Práctico Nro. 4 Resolución de Ecuaciones No Lineales II Problema nro. 1: Para el flujo turbulento de un fluido a través de un tubo liso, es posible establecer la siguiente relación entre el factor de fricción cf y el número de Reynolds Re: 1 cf 0.4 1.74 ln Re cf Calcular cf para Re = 104, 105 y 106. Problema nro. 2: Para el flujo estacionario de un fluido incompresible a través de un tubo rugoso de longitud L y diámetro interior D, la caída de presión viene expresada por la siguiente relación: 2 fM p um L 24 D donde es la densidad del fluido, um es la velocidad media del fluido y fM es el factor de fricción de Moody (adimensional). El factor de fricción de Moody es una función de la rugosidad y del número de Reynolds, Re donde µ es la viscosidad del fluido. Para Re D um 12 µ 2000, fM 64 Re mientras que para Re > 2000, fM viene expresada por la Ecuación de Colebrook, 1 fM 2 log10 3.7 D 2.51 Re fM Un buen punto de arranque para la solución iterativa de esta ecuación puede encontrarse a partir de la Ecuación de Blasius, fM 0.316 Re 0.25 apropiada para flujo turbulento en tubos lisos. A partir de la ecuación de Colebrook, determinar la caída de presión p en el tubo para los siguientes casos: Q gal/min 170 4 D pulgada 3.068 0.622 L pie 10000 100 62.4 80.2 lbm/pie seg. 0.0007 0.05 pulgada 0.002 0.0005 µ Profesores: lbm/pie3 Dr. Ing. Qca. Nicolás J. Scenna Dr. Ing. Qca. Sonia J. Benz Dr. Tgía. Qca. Alejandro S. M. Santa Cruz