CHAPTER 2
Anuncio
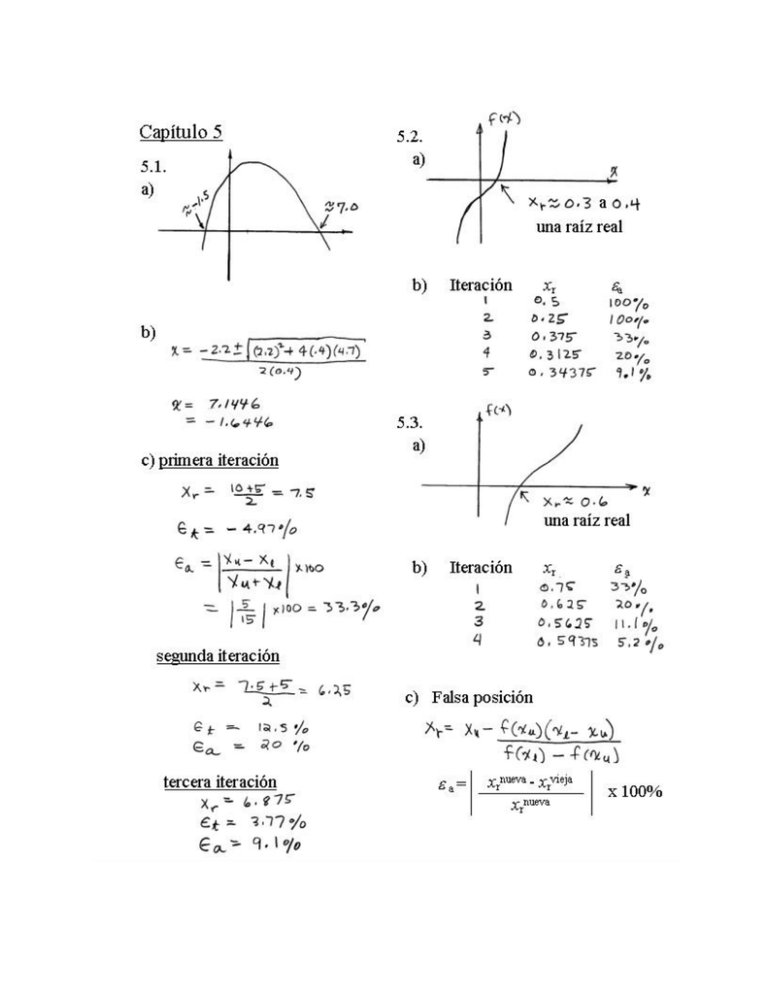
5.13 (a) n= log(35 / .05) = 9.45 o 10 iteraciones log(2) (b) iteración 1 2 3 4 5 6 7 8 9 10 xr 17.5 26.25 30.625 28.4375 27.34375 26.79688 26.52344 26.66016 26.72852 26.76270 para os = 8 mg/L, T = 26.7627 oC para os = 10 mg/L, T = 15.41504 oC para os = 14mg/L, T = 1.538086 oC 5.14 Se presenta un programa en VBA para implementar la función de Bisección (Fig. 5.10) en un programa amable con el usuario: Option Explicit Sub Dim Dim Dim Dim TestBisect() imax As Integer, iter As Integer x As Single, xl As Single, xu As Single es As Single, ea As Single, xr As Single raiz As Single Sheets("Hoja1").Select Range("b4").Select xl = ActiveCell.Value ActiveCell.Offset(1, 0).Select xu = ActiveCell.Value ActiveCell.Offset(1, 0).Select es = ActiveCell.Value ActiveCell.Offset(1, 0).Select imax = ActiveCell.Value Range("b4").Select If f(xl) raiz = MsgBox MsgBox MsgBox MsgBox Else MsgBox End If * f(xu) < 0 Then Bisect(xl, xu, es, imax, xr, iter, ea) "La raíz es: " & raiz "Iteraciones:" & iter "Error estimado: " & ea "f(xr) = " & f(xr) "No hay cambio de signo en el rango inicial" End Sub Function Bisect(xl, xu, es, imax, xr, iter, ea) Dim xrvie As Single, prue As Single iter = 0 Do xrvie = xr xr = (xl + xu) / 2 iter = iter + 1 If xr <> 0 Then ea = Abs((xr - xrvie) / xr) * 100 End If prue = f(xl) * f(xr) If prue < 0 Then xu = xr ElseIf prue > 0 Then xl = xr Else ea = 0 End If If ea < es Or iter >= imax Then Exit Do Loop Bisect = xr End Function Function f(c) f = 9.8 * 68.1 / c * (1 - Exp(-(c / 68.1) * 10)) - 40 End Function Para el ejemplo 5.3, la hoja de cálculo de Excel usada para la entrada se vería así: Ejemplo de Bisección Correr El programa produce una raíz de 14.78027 después de 12 iteraciones. El error aproximado en este punto es 6.63×10−3 %. Todos estos resultados se presentan en formas de cuadros de mensaje. Por ejemplo, la verificación del resultdao se presenta de la siguiente forma: 5.15 Vea las soluciones a los problemas. 5.1 al 5.6 para verificar resultados. 5.16 Errata en el enunciado del problema: Pruebe el programa duplicando el ejemplo 5.5. Se presenta un subprocedimiento en VBApara implementar el método de falsa posición modificada . Está configurado para evaluar el ejemplo 5.5. Option Explicit Sub Dim Dim Dim TestFP() imax As Integer, iter As Integer f As Single, FalsaPos As Single, x As Single, xl As Single xu As Single, es As Single, ea As Single, xr As Single xl = 0 xu = 1.3 es = 0.01 imax = 20 MsgBox "La raíz es: " & FalsaPos(xl, xu, es, imax, xr, iter, ea) MsgBox "Iteraciones: " & iter MsgBox "Error estimado: " & ea End Sub Function FalsaPos(xl, xu, es, imax, xr, iter, ea) Dim il As Integer, iu As Integer Dim xrvie As Single, fl As Single, fu As Single, fr As Single iter = 0 fl = f(xl) fu = f(xu) Do xrvie = xr xr = xu - fu * (xl - xu) / (fl - fu) fr = f(xr) iter = iter + 1 If xr <> 0 Then ea = Abs((xr - xrvie) / xr) * 100 End If If fl * fr < 0 Then xu = xr fu = f(xu) iu = 0 il = il + 1 If il >= 2 Then fl = fl / 2 ElseIf fl * fr > 0 Then xl = xr fl = f(xl) il = 0 iu = iu + 1 If iu >= 2 Then fu = fu / 2 Else ea = 0# End If If ea < es Or iter >= imax Then Exit Do Loop FalsaPos = xr End Function Function f(x) f = x ^ 10 - 1 End Function Cuando el programa se corre para el ejemplo 5.5, produce: La raíz es: 14.7802 Iteraciones: 5 Error estimado: 3.9×10−5 % 5.17 Errata en el enunciado del problema: Use el subprograma que desarrolló en el problema 5.16 para volver a realizar el cálculo del ejemplo 5.6. Los resultados se grafican de la siguiente forma ea% et,% es,% 1000 100 10 1 0.1 0.01 0.001 0 4 8 12 Interpretación: Al principio, el método manifiesta convergencia rápida. Sin embargo, conforme se aproxima a la raíz, se acerca a una convergencia cuadrática. Observe también que, después de unas cuantas iteraciones, la estimación del error aproximado tiene la propiedad de que εa > εt. 5.18 Se presenta un subprocedimiento en VBA para implementar el método de falsa posición, con evaluaciones mínimas de la función, configurado para evaluar el ejemplo 5.6. Option Explicit Sub TestFP() Dim imax As Integer, iter As Integer, i As Integer Dim xl As Single, xu As Single, es As Single, ea As Single, xr As Single, fct As Single MsgBox "La raíz es: " & FPMinFctEval(xl, xu, es, imax, xr, iter, ea) MsgBox "Iterationes: " & iter MsgBox "Error estimado: " & ea End Sub Function FPMinFctEval(xl, xu, es, imax, xr, iter, ea) Dim xrvie, prue, fl, fu, fr iter = 0 xl = 0# xu = 1.3 es = 0.01 imax = 50 fl = f(xl) fu = f(xu) xr = (xl + xu) / 2 Do xrvie = xr xr = xu - fu * (xl - xu) / (fl - fu) fr = f(xr) iter = iter + 1 If (xr <> 0) Then ea = Abs((xr - xrvie) / xr) * 100# End If prue = fl * fr If (prue < 0) Then xu = xr fu = fr ElseIf (prue > 0) Then xl = xr fl = fr Else ea = 0# End If If ea < es Or iter >= imax Then Exit Do Loop FPMinFctEval = xr End Function Function f(x) f = x ^ 10 - 1 End Function El programa produce una raís de 0.9996887 después de 39 iteraciones. El error aproximado en este punto es 9.5×10−3 %. Todos estos resultados se despliegan como cuadros de mensaje. El número de evaluaciones de la función para esta versión es 2n+2. Éste es mucho menor que las evaluaciones de la función en el método de falsa posición estándar (5n). 5.19 Resuelva para las reacciones: R1=265 lbs. R2= 285 lbs. Escriba las ecuaciones de las vigas: 0<x<3 x − 265 x = 0 3 M = 265 − 5.55 x 3 M + (16.667 x 2 ) (1) 3<x<6 x−3 2 ) + 150( x − (3)) − 265 x = 0 2 3 2 (2) M = −50 x + 415 x − 150 6<x<10 2 M = 150( x − (3)) + 300( x − 4.5) − 265 x 3 (3) M = −185 x + 1650 10<x<12 M + 100( x − 3)( M + 100(12 − x) = 0 (4) M = 100 x − 1200 Combinando ecuaciones: Dado que la curva cruza el eje entre 6 y 10, utilice (3). (3) M = −185 x + 1650 Establezca x L = 6; xU = 10 M ( x L ) = 540 xr = x L + xU =8 2 xr = 8 + 10 =9 2 xr = 8+9 = 8.5 2 xr = 8.5 + 9 = 8.75 2 xr = 8.75 + 9 = 8.875 2 xr = 8.875 + 9 = 8.9375 2 xr = 8.875 + 8.9375 = 8.90625 2 xr = 8.90625 + 8.9375 = 8.921875 2 M ( xU ) = −200 M ( x R ) = 170 → remplaza x L M ( x L ) = 170 M ( xU ) = −200 M ( x R ) = −15 → remplaza xU M ( x L ) = 170 M ( xU ) = −15 M ( x R ) = 77.5 → remplaza x L M ( x L ) = 77.5 M ( xU ) = −15 M ( x R ) = 31.25 → remplaza x L M ( x L ) = 31.25 M ( xU ) = −15 M ( x R ) = 8.125 → remplaza x L M ( x L ) = 8.125 M ( xU ) = −15 M ( x R ) = −3.4375 → remplaza xU M ( x L ) = 8.125 M ( xU ) = −3.4375 M ( x R ) = 2.34375 → remplaza x L M ( x L ) = 2.34375 M ( xU ) = −3.4375 M ( x R ) = −0.546875 → remplaza xU M ( x L ) = 2.34375 M ( xU ) = −0.546875 xr = 8.90625 + 8.921875 = 8.9140625 2 M ( x R ) = 0.8984 Por lo tanto, x = 8.91 pies 5.20 M = −185 x + 1650 Establezca x L = 6; xU = 10 M ( x L ) = 540 M ( xU ) = −200 x R = xo − M ( xU )( x L − xU ) M ( x L ) − M ( xU ) x R = 10 − − 200(6 − 10) = 8.9189 540 − (−200) M ( x R ) = −2 × 10 −7 ≅ 0 Sólo fue necesaria una iteración. Por lo tanto, x = 8.9189 pies








