SISTEMAS MULTICOMPONENTES Propiedades Parciales Molares

Clase6.doc
TERMODINÁMICA QUÍMICA I
1
TERMODINÁMICA QUÍMICA I
+
=
+
+
−
2
=
+
9
;
<9
:
;:
<
;
2
46 7 45
53
52
53
528
67
53
528
3
6
53
2
62
5
SISTEMAS MULTICOMPONENTES
Clase6.doc
, entonces:
Propiedades Parciales Molares
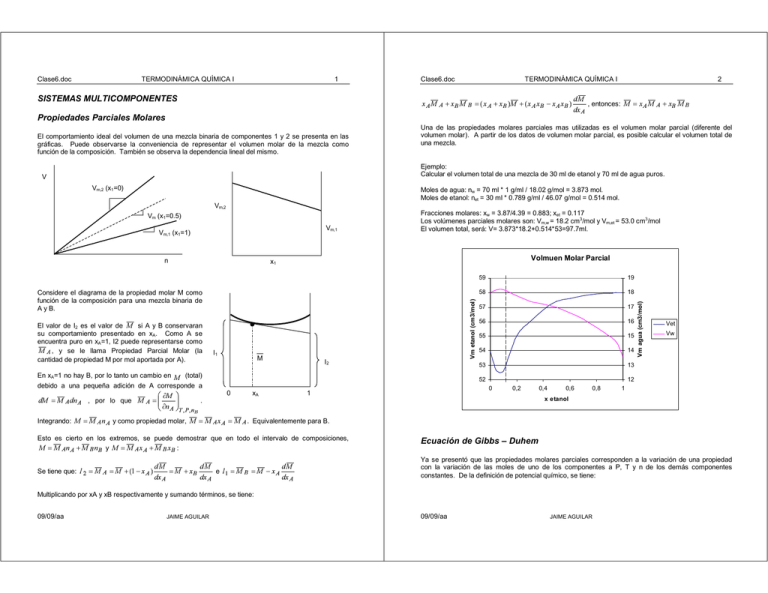
El comportamiento ideal del volumen de una mezcla binaria de componentes 1 y 2 se presenta en las
gráficas. Puede observarse la conveniencia de representar el volumen molar de la mezcla como
función de la composición. También se observa la dependencia lineal del mismo.
Una de las propiedades molares parciales mas utilizadas es el volumen molar parcial (diferente del
volumen molar). A partir de los datos de volumen molar parcial, es posible calcular el volumen total de
una mezcla.
Ejemplo:
Calcular el volumen total de una mezcla de 30 ml de etanol y 70 ml de agua puros.
V
Vm,2 (x1=0)
Moles de agua: nw = 70 ml * 1 g/ml / 18.02 g/mol = 3.873 mol.
Moles de etanol: net = 30 ml * 0.789 g/ml / 46.07 g/mol = 0.514 mol.
Vm,2
Vm (x1=0.5)
Vm,1
Vm,1 (x1=1)
Volmuen Molar Parcial
x1
si A y B conservaran
El valor de I2 es el valor de
su comportamiento presentado en xA. Como A se
encuentra puro en xA=1, I2 puede representarse como
, y se le llama Propiedad Parcial Molar (la
cantidad de propiedad M por mol aportada por A).
I1
M
Vm etanol (cm3/mol)
Considere el diagrama de la propiedad molar M como
función de la composición para una mezcla binaria de
A y B.
I2
En xA=1 no hay B, por lo tanto un cambio en
(total)
debido a una pequeña adición de A corresponde a
, por lo que
=
Integrando:
=
0
∂
∂
y como propiedad molar,
xA
=
=
+
−
17
56
16
55
15
54
14
53
13
=
+
e
=
JAIME AGUILAR
Vw
12
0,2
0,4
0,6
0,8
1
x etanol
=
−
Ecuación de Gibbs – Duhem
Ya se presentó que las propiedades molares parciales corresponden a la variación de una propiedad
con la variación de las moles de uno de los componentes a P, T y n de los demás componentes
constantes. De la definición de potencial químico, se tiene:
Multiplicando por xA y xB respectivamente y sumando términos, se tiene:
09/09/aa
Vet
. Equivalentemente para B.
/- -.+
.+
/
,
/
01
% #$!
#
$"
%
% #$!
#
'
$!
()
%
!
%
&*
=
57
0
1
=
18
.
Esto es cierto en los extremos, se puede demostrar que en todo el intervalo de composiciones,
=
+
y
=
+
:
Se tiene que:
19
58
52
=
59
Vm agua (cm3/mol)
n
Fracciones molares: xw = 3.87/4.39 = 0.883; xet = 0.117
Los volúmenes parciales molares son: Vm,w = 18.2 cm3/mol y Vm,et = 53.0 cm3/mol
El volumen total, será: V= 3.873*18.2+0.514*53=97.7ml.
09/09/aa
JAIME AGUILAR
Clase6.doc
TERMODINÁMICA QUÍMICA I
µ ,
µ +
µ +
+µ
µ +
=
=µ
.
µ =
µ +
Lo cual da como condición que:
pero también se había mostrado que a T y P constante,
µ , la diferencial de G quedará:
µ +
=
Entonces:
3
es la propiedad parcial molar de la energía libre de Gibbs.
∂
µ =
∂
!
µ = . La principal consecuencia
#
$ #
%
"
Generalizando, se obtiene la ecuación de Gibbs – Duhem:
#
&
,
&
'
)
+
*
(
,
(
'
)
*
+
de esta ecuación es que debe cumplirse con esta restricción para validar la toma de datos
experimentales, pues en una mezcla las propiedades parciales molares no deben comportarse
independientemente, dándose origen a los Test de Consistencia Termodinámica. Por ejemplo, para el
caso del volumen molar parcial, debe darse la condición de que:
=−
.
Cálculo de la Entalpía en Mezclas Líquidas
Existen diferentes métodos para calcular la entalpía en mezclas, un de ellos es la entalpía de exceso
Entalpía de Exceso
2
3
.
.
−
-
=
2
0
/
2
−
2
2
1
=
.
Las entalpías en exceso se pueden expresar como polinomios obtenidos a partir de datos
experimentales.
Ejemplo:
Para una mezcla binaria de etanol – agua se tiene que la entalpía en exceso sigue la expresión:
]} (en J/mol)
4
9
−
=
:
;
+
>
9
B
16904,9
10202,5
8597,94
=
−
5
:
;
9
A
-7141,69
-3256,00
-1232,40
+
?
−
=
:
;
+
@
9
[
A
−
=
+
6
7
8
{
:
;
9
=
T(°C)
70
90
110
−
B
=
:
;
C
D
<
=
C
-16370,9
-8892,13
-9503,59
D
9138,04
4086,53
5425,97
E
-2535,6
-1117,92
-1325,26
Ejemplo:
Calcular la entalpía de una mezcla a 70°C de etanol (1) – agua (2) de composición molar x1 = 0.3.
Cpagua = 4180 J/kgK = 75.24 J/molK
Cpetanol = 2470 J/kgK = 113.62 J/molK
09/09/aa
JAIME AGUILAR