Precipitación efectiva
Anuncio
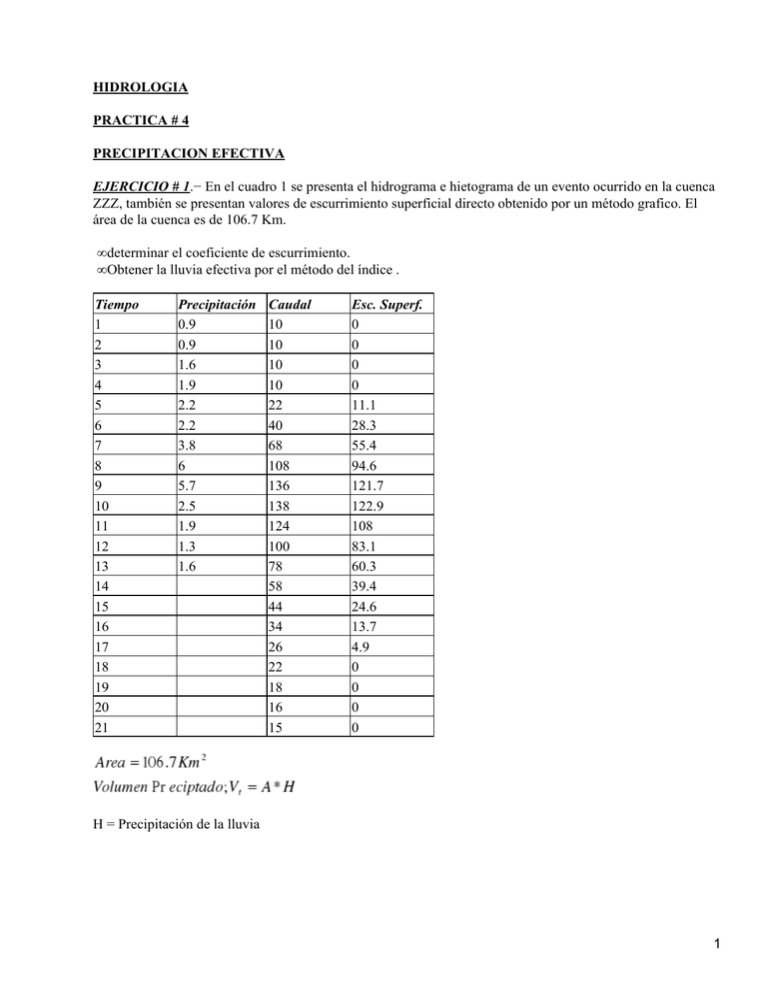
HIDROLOGIA PRACTICA # 4 PRECIPITACION EFECTIVA EJERCICIO # 1.− En el cuadro 1 se presenta el hidrograma e hietograma de un evento ocurrido en la cuenca ZZZ, también se presentan valores de escurrimiento superficial directo obtenido por un método grafico. El área de la cuenca es de 106.7 Km. • determinar el coeficiente de escurrimiento. • Obtener la lluvia efectiva por el método del índice . Tiempo 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Precipitación 0.9 0.9 1.6 1.9 2.2 2.2 3.8 6 5.7 2.5 1.9 1.3 1.6 Caudal 10 10 10 10 22 40 68 108 136 138 124 100 78 58 44 34 26 22 18 16 15 Esc. Superf. 0 0 0 0 11.1 28.3 55.4 94.6 121.7 122.9 108 83.1 60.3 39.4 24.6 13.7 4.9 0 0 0 0 H = Precipitación de la lluvia 1 Maximo Valor = 138 Flujo Base = 10 Base esta comprendida entre los tiempos de 4 y 17 Base= 17−4 = 13 Altura = Maximo Valor − Flujo Base = 138−10 EJERCICIO # 2.−Usando los datos de precipitación y escurrimiento del ejercicio 1. Determinar una estimación del número de curva CN de acuerdo a la metodología del SCS, con este valor determinar la lluvia efectiva. 2 Tiempo 1 2 3 4 5 6 7 8 9 10 11 12 13 Precipitacion 0,9 0,9 1,6 1,9 2,2 2,2 3,8 6 5,7 2,5 1,9 1,3 1,6 P. Acumul. 0,9 1,8 3,4 5,3 7,5 9,7 13,5 19,5 25,2 27,7 29,6 30,4 32,5 Pef. Acum. 0 0 0 0 0,150778816 0,564431487 1,764829396 4,572335601 7,952008032 9,593881453 10,89464945 11,45472727 12,95691769 Pef. 0 0 0 0 0,150778816 0,413652671 1,200397909 2,807506205 3,379672431 1,641873421 1,300767993 0,560077826 1,502190416 EJERCICO #3.−Considerar una cuenca con CN=85, calcular el hietograma de lluvia efectiva correspondiente al siguiente hietograma. 3 Tiempo 0,5 1 1,5 2 2,5 3 3,5 4 Precipitacion 5 8 2 42,3 25 3 10,5 5 P. Acumul. 5 13 15 57,3 82,3 85,3 95,8 100,8 Pef. Acum. 0 1,20754717 1,818181818 28,11192189 48,85764513 51,46121309 60,71163476 65,18210227 Pef. 0 1,20754717 0,610634648 26,29374007 20,74572324 2,603567954 9,250421668 4,470467516 EJERCICIO #4 Calcular el CN promedio de una cuenca con área de drenaje de 3km², siendo 2 km² de suelo B y 1 km² de suelo C, con la siguiente ocupación: Suelo B: 0.3 km² con calles pavimentadas y estacionamiento 1.1 km² uso residencial, lotes de 500m² 0.6 km² áreas comerciales Suelo C : 0.2 km² áreas residenciales, lotes de 1000 m² 0.3 km² parques y jardines en buenas condiciones 0.4 km² área preservada (bosque en buenas condiciones) 0.1 km² calle pavimentadas y estacionamientos Por Tablas determinamos los valores de CN para cada tipo de suelo y su caracteristica • Calles Pavimentadas y estacionamientos = 98 • Uso residencial = 85 • Areas Comerciales = 92 • Areas residenciales = 83 • Parques y Jardines en buenas condiciones = 74 • Area Prerreservada = 70 • Calle Pavimentada y estacionamientos = 98 EJERCICIO#5 En una prueba de infiltración realizada con un infiltrómetro de 30 cm de diámetro, se obtuvieron los datos y resultados que se citan en el Cuadro 1. Se pide: • Una gráfica de la curva de capacidad de infiltración. • La capacidad de infiltración inicial (f0) • Ajustar a los datos la curva de infiltración de Horton • Con la ecuación de Horton determinar la lamina infiltrada desde el tiempo t=0 a t=40 min. La infiltración acumulada se puede calcular con la siguiente relación: 4 Cuadro 1: Ensayo de infiltración: suelo franco − arenoso. Diámetro del cilindro: D=30cm Volumen adicionado Tiempo en que se infiltro volumen (cm3) 0 278 380 515 751 576 845 530 720 (minutos) 0 2 3 5 10 10 30 30 60 Tiempo en que Volumen se infiltro adicionado volumen (cm3) (min) 278 2 380 3 515 5 751 10 576 10 845 30 530 30 720 60 f (mm/h) 117.99 107.52 87.43 63.75 48.89 23.91 15.00 10.19 ( f − fc ) (mm/h) 107.8 97.33 77.24 53.56 38.71 13.72 4.81 0.00 Y= 4,68 − 0,043 * X Tiempo f (min) 2 5 10 20 30 60 90 150 (mm/h) A = (ð * D2)/4 = 117.99 A (cm2) = 706.86 107.52 87.43 63.75 48.89 23.91 15.00 10.19 x (min) 1 3.5 7.5 15 25 45 75 120 y (mm/h) 4.68 4.58 4.35 3.98 3.66 2.62 1.57 K= 23.38 5 f − fc = f= 107.8 117.96 F = 10.19+ 107.8 * e −0.043 t Para un t = 0 , t= 40 t= 0 F = 0 t= 40 F = 2477.18 EJERCICIO#6. En una cuenca de 30 Km2, se midieron el hietograma y el hidrograma mostrados en el Cuadro 2. Determinar el coeficiente de escurrimiento para esta cuenca. Cuadro 2: Precipitación y caudal medidos simultáneamente Tiempo (horas) 1 2 3 4 5 Precipitación (mm) 3.07 2.79 4.45 2.2 0.6 Tiempo (horas) 0 2 4 6 8 10 12 14 16 Caudal (m3/s) 1 1 1 3 6 5 3 1 1 Ht = 18.51mm A = 30*106 Vt = Vesd = Coef escurr= 555300 90000 0.16 El porcentaje de escurrimiento es del 16 % EJERCICIO #7 Desarrolle una respuesta para las siguientes preguntas • Que significa el coeficiente de escurrimiento ? El porcentaje de escurrimiento que ocurre • Que tipo de mediciones de campo son necesarios para determinar el índice FI ? Para determinar el indice FI son necesarias Mediciones de lluvia y caudal 6 • El método de Horton o el índice FI, describen mejor la infiltración cuando ocurre un evento de tormenta ? Si, por que se aplican a capacidades de infiltraciones mayores • Cual es la utilidad del índice FI ? Calcular la lluvia efectiva que se va ha convertir en escurrimiento • Asumir que ya logramos obtener la lluvia efectiva, el escurrimiento a la salida de la cuenca en términos del caudal máximo dependerá del tipo de suelo ? Si, por que depende de la cobertura vegetal o del tipo de asentamientos urbanos que halla en el suelo • El método de Horton refleja la recuperación de la capacidad de infiltración cuando deja de llover ? Refleja la variación de la capacidad de infiltración cuando llueve • Para que tipo de situaciones se requiere representar la capacidad de infiltración cuando deja de llover y en que caso esto no es necesario ? Se requiere representar la capacidad de infiltración en situaciones que se necesita conocer la cantidad de agua de escurrimiento y de agua almacenada en el subsuelo, esto para prevenir inundaciones y daños hidrológicos, como también para beneficio, es decir para situaciones de riego, es necesario conocer la cantidad de agua existente en el subsuelo para fines agrícolas • Después de calcular la lluvia efectiva la transformaremos en caudal, esta transformación depende del tipo de suelo ? Si porque las perdidas iniciales y la infiltración están de acuerdo con el tipo de suelo • Cual es la limitación en términos de equipos de medición que vienen a subsanar los coeficientes de desagregación ? Gracias a los coeficientes de desagregación, se facilita el uso de los pluviómetros en las cuencas, ya que con ellos se pueden calcular precipitaciones en intervalos de tiempo menores a un día Flujo Base 128 13*30 7











