Análisis modal en tapas de guitarra según su diseño de varillaje
Anuncio

RAE
1.
2.
3.
4.
5.
6.
TIPO DE DOCUMENTO: Trabajo de grado para optar por el título de INGENIERO DE SONIDO
TÍTULO: ANÁLISIS MODAL EN TAPAS DE GUITARRA SEGÚN SU DISEÑO DE VARILLAJE
AUTORES: Mario Esteban Eraso Rosada, Estefanía Riveros Ramírez
LUGAR: Bogotá, D.C
FECHA: 27 de Octubre de 2014
PALABRAS CLAVE: Tapa armónica, modos normales de vibración, método de elementos finitos, patrones de
Chladni, análisis modal, diseño de varillaje, guitarra.
7. DESCRIPCIÓN DEL TRABAJO: En el campo ingenieril surge la necesidad de obtener registros sonoros de alta
calidad, lo cual precisa conocer el comportamiento acústico de cada instrumento musical, así como buscar la
optimización de las técnicas de construcción, gracias a la profundización en su fundamento físico. Esto lleva a
realizar mediciones que indiquen cada característica específica del instrumento, como es el comportamiento
modal mediante la visualización de patrones Chladni junto a la simulación por ordenador a través del método de
los elementos finitos.
8. LÍNEAS DE INVESTIGACION: Línea de Investigación de la USB: Tecnologías actuales y Sociedad. Sub línea
de Facultad de Ingeniería: Análisis y Procesamiento de Señales. Campo Temático del Programa: Acústica.
9. METODOLOGÍA: La investigación implementa pruebas experimentales de medición, análisis y respectivas
interpretaciones del comportamiento modal de la tapa armónica de la guitarra, junto a simulaciones por
elementos finitos. Por tanto el enfoque del proyecto es empírico-analítico.
10. CONCLUSIONES:
El primer modo de vibración forma la misma figura en las cuatro superficies, el máximo nivel de energía se
concentra en el centro de la tapa y ocupa una región ovalada de tamaño considerable, no obstante en el
diseño Folk, la figura tiende a alargarse hacia la boca como consecuencia de la disposición en X de los
refuerzos principales y la ausencia de la barra transversal inferior a la boca presente en los demás diseños.
Las figuras del segundo modo de las cuatro tapas forman dos regiones de concentración de energía. Sin
embargo, los diseños Clásico y Flamenco alcanzan un nivel energético inferior debido a que la configuración
en abanico disipa la energía. La tapa sin varillaje produce en su tercer modo dos regiones simétricas respecto
al eje vertical que abarcan el largo de la superficie y centralizan toda la energía en la parte más ancha. Al
agregar las barras de refuerzo del mástil alrededor de la boca en las tapas Clásica y Flamenca, estos cúmulos
sólo ocupan la zona comprendida por las barras en abanico. En la guitarra Folk esta figura deja de ser
simétrica, puesto que la disposición de sus barras tampoco lo es. El cuarto modo de vibración, presenta tres
zonas de concentración de energía, donde los valores máximos se distribuyen en diferentes regiones
dependiendo de cada diseño. La tapa sin varillaje refleja un único valor pico en la zona superior, mientras en la
tapa Folk, en la zona inferior, donde hay mayor libertad de vibración gracias al reducido número de barras. La
guitarra Clásica y Flamenca dejan la parte baja de la guitarra con menor energía debido a la presencia del
refuerzo en abanico. La configuración de las barras de cada diseño estudiado experimenta las mayores
diferencias modales en el quinto modo de vibración.
Los resultados de los diseños de las tapas Flamenca y Clásica mantienen los mismos patrones en las figuras
modales, con cambios en sus frecuencias de resonancia guardando valores cercanos. Esto indica que las
barras adicionales ubicadas en la parte inferior de la guitarra flamenca no representan un cambio significativo
en el comportamiento modal de dichos diseños.
Ambos métodos muestran un alto grado de correlación al comparar las figuras modales de las cuatro tapas
armónicas escogidas, siendo el diseño Folk aquél que conserva mayores similitudes.
En el cuarto modo de vibración de las tapas Clásica y Flamenca, las imágenes arrojadas por la simulación
exponen dos cúmulos de energía claramente separados entre sí en la zona inferior de la placa, mientras que las
figuras halladas en la medición tienden a formar un mismo foco de energía. Lo cual indica que la barra del eje
central perteneciente al abanico al vibrar dispersa, a través de su longitud, los dos cúmulos energía.
Las frecuencias fundamentales de las tapas con diseños específicos de varillaje aumentan en relación a la tapa
sin barras, debido a la modificación de la rigidez sobre la placa al adicionar dicho refuerzo. La tapa con la menor
frecuencia fue aquella sin diseño, seguida ascendentemente de la Flamenca, Clásica y Folk.
Las frecuencias de resonancia adquiridas mediante simulación fueron menores a las resultantes del método
experimental en la mayoría de los datos, únicamente seis modos de vibración presentaron valores mayores,
entre los cuales están el quinto modo de la tapa sin varillaje, el cuarto y quinto modo de la tapa Clásica, el
cuarto modo de la tapa Flamenca y el segundo y quinto modo de la tapa Folk. En los cuatro casos las
frecuencias fundamentales fueron menores en los resultados de la simulación.
ANÁLISIS MODAL EN TAPAS DE GUITARRA SEGÚN SU DISEÑO DE VARILLAJE
MARIO ESTEBAN ERASO ROSADA
ESTEFANÍA RIVEROS RAMÍREZ
UNIVERSIDAD DE SAN BUENAVENTURA BOGOTÁ
FACULTAD DE INGENIERÍA
INGENIERÍA DE SONIDO
BOGOTÁ D.C
2014
ANÁLISIS MODAL EN TAPAS DE GUITARRA SEGÚN SU DISEÑO DE VARILLAJE
MARIO ESTEBAN ERASO ROSADA
ESTEFANÍA RIVEROS RAMÍREZ
PROYECTO DE GRADO
Tutor
LUIS JORGE HERRERA FERNÁNDEZ
Físico
Máster en Ingeniería Acústica en la Industria y el Transporte
UNIVERSIDAD DE SAN BUENAVENTURA BOGOTÁ
FACULTAD DE INGENIERÍA
INGENIERÍA DE SONIDO
BOGOTÁ D.C
2014
CONTENIDO
INTRODUCCIÓN .......................................................................................................................... 10
1. PLANTEAMIENTO DEL PROBLEMA ...................................................................................... 11
1.1 ANTECEDENTES .................................................................................................................................. 11
1.2 DESCRIPCIÓN Y FORMULACIÓN DEL PROBLEMA ......................................................................... 15
1.3 JUSTIFICACIÓN .................................................................................................................................... 16
1.4 OBJETIVOS ........................................................................................................................................... 16
1.4.1 OBJETIVO GENERAL ................................................................................................................... 16
1.4.1 OBJETIVOS ESPECÍFICOS .......................................................................................................... 16
1.5 ALCANCES Y LIMITACIONES ............................................................................................................. 16
2. MARCO DE REFERENCIA ....................................................................................................... 18
2.1 MARCO TEÓRICO CONCEPTUAL ...................................................................................................... 18
2.1.1 La guitarra ..................................................................................................................................... 18
2.1.2 La tapa armónica .......................................................................................................................... 18
2.1.3 Modos normales de vibración ..................................................................................................... 20
2.1.4 Materiales elásticos ...................................................................................................................... 20
2.1.5 Módulo de Young (Módulo de elasticidad longitudinal) ........................................................... 21
2.1.6 Módulo de Cizalladura (Módulo de elasticidad transversal) .................................................... 22
2.1.7 Coeficiente de Poisson ................................................................................................................ 23
2.1.8 Materiales ortotrópicos ................................................................................................................ 24
2.1.9 Método de elementos finitos (MEF). ........................................................................................... 24
2.1.10 Grados de libertad ...................................................................................................................... 25
2.1.11 Patrones Sonoros de Chladni ................................................................................................... 26
3. METODOLOGIA ....................................................................................................................... 27
3.1 ENFOQUE DE LA INVESTIGACION .................................................................................................... 27
3.2 LÍNEA DE INVESTIGACION, SUBLINEA Y CAMPO TEMATICO ....................................................... 27
3.3 TÉCNICAS DE RECOLECCION DE INFORMACIÓN .......................................................................... 27
3.4 HIPÓTESIS ............................................................................................................................................ 27
3.5 VARIABLES .......................................................................................................................................... 27
3.5.1 VARIABLES INDEPENDIENTES .................................................................................................. 27
3.5.2 VARIABLES DEPENDIENTES ...................................................................................................... 27
4. PRESENTACIÓN Y ANÁLISIS DE LOS RESULTADOS .......................................................... 28
4.1 Características de las tapa a estudiar ................................................................................................ 28
4.2 Modelamiento de problemas dinámicos por método de elementos finitos ................................... 31
4.3 Simulación por elementos finitos ...................................................................................................... 34
4.3.1 Pre-Proceso ................................................................................................................................... 35
4.3.2 Solución ......................................................................................................................................... 47
4.3.3 Post-Proceso ................................................................................................................................. 49
4.4 Visualización de Figuras Chladni ....................................................................................................... 50
4.4.1 Esquema de medición .................................................................................................................. 50
4.4.2 Medición del parlante ................................................................................................................... 53
5. ANÁLISIS DE RESULTADOS .................................................................................................. 55
5.1 Simulación por elementos finitos ...................................................................................................... 55
5.2 Patrones modales de Chladni ............................................................................................................. 58
6. CONCLUSIONES ..................................................................................................................... 62
RECOMENDACIONES ................................................................................................................. 64
REFERENCIAS............................................................................................................................. 65
Bibliografía.................................................................................................................................................. 65
Sitios revisados en Internet ...................................................................................................................... 66
ANEXOS ....................................................................................................................................... 67
Anexo A. Simulación tapa armónica sin varillaje ................................................................................... 67
Anexo B. Simulacióntapa armónica Clásica ........................................................................................... 69
Anexo C. Simulación tapa armónica Flamenca ...................................................................................... 72
Anexo D. Simulación tapa armónica Folk ............................................................................................... 74
Anexo E. Medición tapa armónica sin varillaje ....................................................................................... 77
Anexo F. Medición tapa armónica Clásica .............................................................................................. 78
Anexo G. Medición tapa armónica Flamenca.......................................................................................... 80
Anexo H. Medición tapa armónica Folk ................................................................................................... 81
LISTA DE TABLAS
Tabla 1. Dimensiones varillaje de tapa clásica.
Tabla 2. Dimensiones varillaje de tapa flamenca.
Tabla 3. Dimensiones varillaje de tapa flamenca.
Tabla 4. Constantes elásticas de la madera estudiada.
Tabla 5. Especificaciones físicas del material.
Tabla 6. Número de elementos en cada modelo.
Tabla 7. Frecuencias de resonancias simuladas.
Tabla 8. Frecuencias de resonancias medidas.
Tabla 9. Comparación de frecuencias. Tapa sin varillaje.
Tabla 10. Comparación de frecuencias. Tapa Clásica.
Tabla 11. Comparación de frecuencias. Tapa Flamenca.
Tabla 12. Comparación de frecuencias. Tapa Folk.
LISTA DE FIGURAS
Figura 1. Corte de láminas de madera.
Figura 2. Diseño de varillaje.
Figura 3. Gráfica de esfuerzo en función de la deformación unitaria para un sólido.
Figura 4. Módulo de Young.
Figura 5. Deformación que presenta un objeto al aplicarle una fuerza.
Figura 6. Módulo de Cizalladura.
Figura 7. Relación de Poisson.
Figura 8. Ejes perpendiculares en la madera.
Figura 9. Registros de Ernst Chladni de patrones modales en placas cuadradas.
Figura 10. De izquierda a derecha. Guitarra clásica, flamenco y folk.
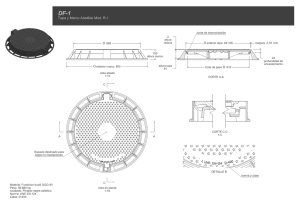
Figura 11. Dimensiones de las tapas.
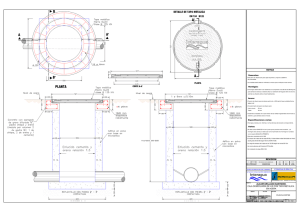
Figura 12. Diseño de varillaje de las tapas a. clásica, b. folk, c. flamenca.
Figura 13. Respuesta armónica para vibraciones libres no amortiguadas.
Figura 14. Elemento Solid 92.
Figura 15. Creación de puntos en Ansys APDL.
Figura 16. Formación de líneas en Ansys APDL.
Figura 17. Función para reflejar la imagen.
Figura 18. Área generada en Ansys APDL.
Figura 19. Creación de la boca en la tapa.
Figura 20. Tapa sin varillaje generada en Ansys APDL.
Figura 21. Tapa Clásica en Ansys APDL.
Figura 22. Tapa Flamenca en Ansys APDL.
Figura 23. Tapa Folk en Ansys APDL.
Figura 24. Malla tapa armónica sin varillaje.
Figura 25. Malla tapa armónica clásica.
Figura 26. Malla tapa armónica flamenca.
Figura 27. Malla tapa armónica folk.
Figura 28. Condiciones de frontera.
Figura 29. Interfaz gráfica de resultados.
Figura 30. Soporte para las tapas.
Figura 31. Parlante utilizado en las mediciones.
Figura 32. Soporte para parlante.
Figura 33. Esquema de medición.
Figura 34. Superficie con sal de cocina.
Figura 35. Esquema de medición del transductor.
Figura 36. Montaje de medición del transductor.
Figura 37. Gráfica de respuesta en frecuencia del transductor.
Figura 38. Modos de vibración por elementos finitos. Tapa armónica sin varillaje.
Figura 39. Modos de vibración por elementos finitos. Tapa armónica Clásica.
Figura 40. Modos de vibración por elementos finitos. Tapa armónica Flamenca.
Figura 41. Modos de vibración por elementos finitos. Tapa armónica Folk.
Figura 42. Modos de vibración. Tapa armónica sin varillaje.
Figura 43. Modos de vibración. Tapa armónica Clásica.
Figura 44. Modos de vibración. Tapa armónica Flamenca.
Figura 45. Modos de vibración. Tapa armónica Folk.
LISTA DE ANEXOS
Anexo A. Simulación tapa armónica sin varillaje.
Anexo B. Simulación tapa armónica Clásica.
Anexo C. Simulación tapa armónica Flamenca.
Anexo D. Simulación tapa armónica Folk.
Anexo E. Medición tapa armónica sin varillaje.
Anexo F. Medición tapa armónica Clásica.
Anexo G. Medición tapa armónica Flamenca.
Anexo H. Medición tapa armónica Folk.
INTRODUCCIÓN
La guitarra es un instrumento musical de tipo cordófono, compuesto de una caja de madera con un agujero
en el centro de su tapa frontal, y su configuración de 6 cuerdas, como se la conoce en la actualidad, es
descendiente de un instrumento español que data del siglo 16 llamado Vihuela, el cual tiene raíces aún más
profundas en la antigüedad. Se puede considerar a la guitarra como todo un sistema; las cuerdas irradian
solo una pequeña cantidad de energía, pero éstas excitan la tapa frontal, la cual responde transfiriendo
energía a la cavidad de aire y la tapa trasera, de manera que el sonido se emite de manera más eficiente por
todo el sistema en vibración. Diversos fabricantes concuerdan en que uno de los pilares vitales para la
obtención de un sonido de calidad, a partir de su construcción, es el uso de un diseño apropiado para la tapa
frontal de la guitarra, en donde converjan detalles significativos en su sonido, como un buen alcance en
tonos brillantes, buena amplificación de bajos y una resonancia prolongada. Su peso debe serlo
suficientemente liviano para amplificar la vibración producida por las cuerdas y al mismo tiempo, debe ser
rígida para mantener su estructura y no romperse debido a la constante fuerza que se le aplica a través de
las mismas. Con ese fin, se le agrega a la tapa una serie de varillas que modifican la forma en que el
sistema vibra, el diseño de dicho varillaje depende de los objetivos que el Luthier busque cumplir (agregar
rigidez, modificar resonancia, etc), o simplemente sea el producto experimental del fabricante.
Con el fin de conocer qué aspectos en la tapa se modifican a partir del uso de dichos diseños, se realiza el
análisis de comportamiento modal de varias tapas de guitarra que constan de diferentes diseños de varillaje,
variando el número de barras y distribución de las mismas a lo largo de la superficie de la tapa.
De primera mano, se lleva a cabo un modelamiento de las tapas por computador aplicando el método de
elementos finitos, el cual permite obtener, de manera simulada, los procesos vibratorios que entran en juego
en cada tapa, y cómo se modifican dependiendo de su respectivo diseño de varillaje. Por otro lado, se
realiza un proceso experimental que proporcione resultados reales para ser cotejados con los resultados
simulados. Para ello, mediante la técnica de formación de patrones sonoros de Chladni, se efectúa la
captura de los estados vibratorios de cada tapa, y de esa forma es posible observar los modos normales de
vibración de cada una y así discernir detalles que varíen en cada diseño.
Los procesos desarrollados y ejecutados en esta investigación permiten comprender por qué la importancia
de la introducción de un sistema de varillaje en la guitarra acústica, y cómo ésta modificación en su
estructura configura características en el sonido resultante de la misma. Así mismo, la medición y
caracterización de un instrumento musical, permite un acercamiento entre fabricante, ejecutante e ingeniero,
optimizando recursos, diseño y fabricación del mismo.
1. PLANTEAMIENTO DEL PROBLEMA
1.1 ANTECEDENTES
Guitar Top-Plate Modelling Using Finite Element Method Techniques. Derek O'Gorman and Dermot J.
Furlong. Trinity College. Dublin, Ireland.
Artículo que se encuentra en la base de datos de la Audio Engineering Society y fue presentado en el año de
1996. Presenta un estudio sobre el comportamiento modal de dos tapas de guitarras fabricadas por el luthier
norirlandés George Lowden, modelos 1994 y 1995. Se investiga los efectos del varillaje sobre las mismas, el
cual variaba ligeramente entre ambas en cuanto al número y distribución. En el texto se habla sobre detalles
físicos a tener en cuenta en la guitarra como la interacción entre la tapa y las cuerdas, las cualidades que
debe tener una guitarra de buena calidad, como un buen alcance en tonos brillantes, buena amplificación de
bajos y resonancia prolongada; y algunos aspectos sobre el comportamiento de la energía acústica dentro
del cuerpo de la guitarra a nivel modal y frecuencial. Se realiza una simulación de elementos finitos
mostrando los patrones modales en ambas tapas y se comprueba que si existe una variación en cuanto a la
distribución de los modos entre ambas tapas. Los resultados se compararon con mediciones experimentales
de patrones de Chladni para validar el modelamiento y obtener resultados similares.
En el experimento realizado para generar los modos de vibración que forman los patrones o figuras de
Chladni se construye una base que permite afirmar las tapas en los bordes, y se le agrega arena fina a la
superficie. La prueba se divide en dos, en la primera se utiliza un vibrador Ling Dynamic Systems Model
200, usado para excitar la tapa en varios puntos alrededor de la misma. En la segunda parte se utiliza un
altavoz suspendido a una distancia nominal apuntando directamente a las tapas para inyectarle energía al
sistema. Para ambos caso se utilizó un generador de onda y las pruebas resultaron en la distribución de la
arena de acuerdo al patrón modal que se generara. Los resultados combinados de estas dos técnicas
prueban que el modelo es aceptable y acertado para arrojar información acerca de la naturaleza de las
tapas.
El diseño de varillaje de cada tapa contiene características similares. Fabricadas con madera de cedro,
implementan un refuerzo en X típicamente utilizado en guitarras de cuerdas de acero, que junto a los
refuerzos ubicados en la parte superior de la tapa, sirven para proveer integridad estructural. Se adicionan
costillas de manera que el modelo 1994 cuenta con ocho barras, mientras que el modelo 1995 usa diez
(cuatro barras de menor tamaño y distinta orientación).
El análisis de resultados del artículo se centra principalmente en comparar las figuras modales que se
obtienen por medio de la simulación en ambos diseños. Adicionalmente se realiza una relación entre
frecuencias modales y notas que ejecutadas en las guitarras presentan problemas, sin embargo no se
especifica la implementación de una técnica ingenieril que compruebe dichas dificultades o que permita el
correcto análisis de dichas notas junto a la posterior correlación con los datos entregados por el método de
elementos finitos.
La formación de patrones de Chladni es usada para corroborar aquellos modelos entregados por el método
de elementos finitos con el fin de determinar si existe precisión entre ambas técnicas, por lo que los autores
concluyen que los resultados suministrados por las simulaciones son válidos y satisfactorios.
Analysis and minimization of unwanted Resonances in Loudspeaker Systems via FEM techniques.
Mario Di Cola, Davide Doldi, Marco Mocellin, Ing. Rinaldo Griforini, Paolo Antinori, Remo Orsoni,
Giorgio Santarelli. Audio Labs Systems, Proel Sound Reinforcement Division. Italia.
Artículo presentado en la convención de la AES número 116 del año 2004. Los autores buscan localizar y
minimizar resonancias que se producen en la estructura de altavoces debido a la alta presión generada por
los transductores hacia afuera de la cabina y en las mismas cantidades hacia dentro del sistema,
formándose modos estructurales en la cabina que pueden llegar a ser audibles, comprometiendo la calidad
acústica del producto. Por tanto se utiliza el método de elementos finitos para analizar y predecir
resonancias estructurales, incluso el mismo método puede ser usado para estudiar sistemas existentes y
mejorar su rendimiento. Los autores muestran un procedimiento experimental y validan los resultados con
mediciones modales.
Se comienza dando una introducción a las bases del análisis estructural por medio de elementos finitos y se
explica el proceso teórico que se debe tener en cuenta, como la discretización de elementos, objetos Shell y
Plane, el procesamiento, entre otros conceptos.
Se realiza un estudio de la cabina de unos altavoces marca Proel modelo 212 SP, construida con madera de
contrachapado de abedul y cuya geometría es modelada en un software CAD. La simulación se lleva a cabo
utilizando elementos Shell, dado que el espesor de la madera supera diez veces el ancho de las placas, esta
relación es generalmente considerada la mínima para trabajar con este tipo de elementos. Para reducir el
número de elementos se utilizan aquellos que trabajan con cuatro nodos.
Mediante la simulación y visualización de resultados se pueden establecer los modos de vibración más
significativos causantes de deformaciones amplias y por tanto resultando en perturbaciones acústicas
mayores, además de establecer los paneles de mayor influencia en las vibraciones. Posteriormente se
realiza una nueva simulación agregándole al modelo refuerzos con paneles de acero de 2 y 3 mm de grosor,
dándole un aumento a la rigidez del sistema y reduciendo de manera significativa la amplitud de las
vibraciones en los modos más influyentes. De manera similar se realiza un estudio sobre la cabina del
altavoz Proel Next 8, para el cual se realiza el modelo de sus paneles y se obtiene los modos de resonancia
mediante el método de elementos finitos.
The Violin: Chladni patterns, plates, shells and sounds. C. Cough. School of Physics and Astronomy,
University of Birmingham. Birmingham, Reino Unido.
Artículo presentado en la Revista de Física Europea. Se consideran las vibraciones y el sonido emitido por
un violín. Las vibraciones se interpretan como modos normales que se generan al frotar las cuerdas con el
arco, acopladas con el puente, la caja resonancia del instrumento y los modos acústicos del lugar en donde
se interpreta violín. En el texto se enfatiza la importancia de la distribución espacial de los patrones modales
en cuanto al acoplamiento de las vibraciones transmitidas desde las cuerdas al cuerpo del instrumento y se
usa el método de las figuras de Chladni como una ayuda para entender la física y optimizar las propiedades
acústicas de las placas durante su construcción. Se hace una descripción detallada del funcionamiento del
violín, es decir, se describe el mecanismo que éste utiliza para radiar sonido y se hace un análisis
matemático para los modos normales del violín considerándolo como un ejemplo simple de vibraciones
transversales en una cuerda estirada con un resonador armónico en uno de sus extremos. Luego se
obtienen ecuaciones que describen el movimiento del oscilador acoplado y bajo la fuerza ejercida en las
cuerdas en términos de modos normales.
Se realizan mediciones de figuras de Chladni sobre el instrumento teniendo como principal referencia las
tapas frontal y posterior, puesto que son los componentes más importantes al determinar la calidad del
sonido. Para el experimento se utiliza un altavoz excitado bajo una función senoidal y sobre la superficie se
rocía escarcha o algún otro material granular fino y liviano. Cuando la frecuencia generada en el parlante se
acopla a algún modo normal de vibración del instrumento, los gránulos de escarcha se trasladan a la
posición de las líneas nodales. Posteriormente se hace un análisis de los modos que resultan, describiendo
su similitud con aquellos que se forman en placas rectangulares y combinaciones de varios modos.
Finalmente explican algunos criterios de diseño que se han realizado sobre violines basándose en la
formación de los modos resonantes.
Adicionalmente el documento cuenta con teoría de vibraciones sobre placas delgadas, simulaciones de lo
que le ocurre en la distribución modal de una tapa de violín antes y después de realizar las aberturas ʃ,
barras de refuerzo, todo el cuerpo acoplado, entre otros análisis.
Obtención y análisis de la respuesta al impulso (IR) del tiple Colombiano mediante el método directo
e inverso. Laura Vanessa Acero Martínez, César Darío Bustos Ortíz, Carolina Guerrero, Stephanie
Murcia, Javier Santana, Juan Martín Aponte, Oscar Esneider Acosta, Luis Fernando Hermida.
Programa de Ingeniería de Sonido. Universidad de San Buenaventura Bogotá.
Artículo publicado en la revista Ingenium de la facultad de ingeniería de la Universidad de San Buenaventura
Sede Bogotá en el año 2010. Se analiza la respuesta al impulso del Tiple colombiano, el cual es un
instrumento musical de cuerda pulsada. Los autores utilizan dos técnicas para capturar la respuesta al
impulso del sistema.
La primera técnica consiste en inyectar una fuerza conocida al instrumento y el sonido generado por éste es
capturado con un micrófono de medición. Se procede a realizar una deconvolución para así obtener la
respuesta al impulso, a este procedimiento se le llama método directo. Con tales fines se diseña un
transductor que funciona como herramienta para aplicar la fuerza externa al sistema. Se construye a partir
de un parlante al cual se le ha retirado el cono reemplazándolo por un cilindro de diámetro muy pequeño (4
mm). También se construye una base que permite ubicar el parlante en forma perpendicular al suelo,
asegurando que su movimiento sea axial y transmita energía al puente del tiple de manera correcta.
El segundo método utilizado es el proceso inverso al mencionado anteriormente. Se excita al instrumento
con un campo sonoro generado por un altoparlante, de manera que el primero entra en vibración. El
movimiento se registra con un acelerómetro ubicado en la superficie del puente. A continuación se realiza
una deconvolución y se obtiene la respuesta al impulso. A este proceso se le conoce como método indirecto.
En ese orden, se utilizó una cabina JBL Eon15 la cual fue calibrada para lograr en ella un comportamiento
plano dentro del ancho de banda del acelerómetro, y fue ubicada frente al cuerpo del tiple mientras éste se
encontraba suspendido de forma vertical.
Los autores obtienen entonces las respuestas al impulso del instrumento mediante ambos métodos a las
cuales se les aplica la Transformada Rápida de Fourier (FFT) haciendo posible observar las frecuencias de
resonancia generadas por el tiple concluyendo que ambos métodos arrojan resultados similares sin importar
la técnica aplicada. Ambos procedimientos muestran que el tiple presenta una respuesta pobre en
frecuencias por debajo de 100 Hz y se tiene picos de energía considerables alrededor de 110 Hz, 220 Hz y
460 Hz.
Argumentan que el uso de ambas técnicas brinda una visión más amplia del comportamiento del instrumento
puesto que el método indirecto entrega la información de la zona entre 100 Hz y 2 KHz, mientras que el
directo permite observar detalles por encima de 2 KHz.
Análisis acústico de un recinto variando su geometría, por medio del método de elementos finitos.
Julián Mauricio Barreiro Pérez, Rainer Enrique Bodensiek Cuervo. Programa de Ingeniería de Sonido.
Universidad de San Buenaventura Bogotá.
Trabajo de tesis presentado en la universidad de San Buenaventura en el programa de ingeniería de Sonido
en el año 2010. El trabajo implementa un método numérico (método de elementos finitos) para la predicción
acústico-arquitectónica, el cual permite tener en cuenta cualquier elemento de su diseño por más pequeño,
grande o irregular que sea. El resultado final compara las simulaciones de distribución energética en un
recinto acústico, variando su geometría.
Los autores hacen en primera instancia un modelo de un recinto regular (paralelepípedo) al cual se le realiza
el análisis de elementos finitos y se continúa modelando otros espacios con variaciones provenientes del
primero, éstas se implementan por ser utilizadas como posibles soluciones a problemas acústicos. Se
presentan entonces inclinaciones, formas irregulares en paredes, inserción de difusores QRD, uso material
absorbente y la mezcla de todas las anteriores.
Durante el desarrollo del documento se explican algunos detalles importantes a tener en cuenta durante la
utilización del software de simulación como importación de geometrías a Ansys desde otros programas de
diseño asistido por computadora y conceptos que se manejan dentro de la estructura de Ansys como el
preprocesador, solucionador, post-procesador, cargas en el modelo, enmallado, entre otros; y define algunos
comandos que se utilizan en la simulación, en este caso los que especifican el tipo de análisis, el tipo de
elemento, ubicación de puntos, atributos, constantes que se escriben en la ventana de consola del
programa, entre otros.
El proyecto brinda una excelente perspectiva de desarrollo, debido a que cuenta con procesos de simulación
detallados proporcionados por los desarrolladores del software de simulación por elementos finitos: Ansys.
Figuras de Chladni en tambores. Jaime Arango, León Escobar, Carlos Reyes. Universidad del Valle,
Cali, Colombia.
Artículo publicado en la edición número 33 en la revista Lecturas Matemáticas del año 2012. Los autores
hacen un acercamiento matemático a la generación de figuras de Chladni en placas vibrantes con borde
libre y se realiza un experimento para medición de las figuras que se forman sobre la membrana de una caja
vallenata (instrumento de música vallenata tradicional, similar a una tambora). Esta puede verse como una
placa de parche acrílico adherida firmemente con un aro metálico a una caja de resonancia del mismo
material pero de mayor espesor. Para lograr la vibración en el parche se utiliza un montaje experimental
basado en trabajos de Thomas D. Rossing, el cual consiste en emitir una señal eléctrica senoidal mediante
un generador de ondas, monitoreado con un multímetro digital. Se emplea un amplificador de potencia de
audio, para darle mayor fuerza eléctrica a la señal, alimentando un sistema de bobinas ubicadas unos
centímetros arriba y abajo de la membrana. Éstos interactúan con imanes adheridos a la membrana
generando campos magnéticos alternantes y produciendo oscilaciones periódicas. Las figuras se forman a
partir de un material granular (sal común en este caso) previamente distribuido de manera homogénea sobre
la superficie a medir. La membrana vibra según las oscilaciones generadas por el sistema de bobinas e
imanes dando lugar a las figuras producidas por los modos normales de vibración en la superficie.
Análisis Acústico de la Gaita Colombiana. Luis Sarmiento Molina. Gustavo Pérez Jiménez. Programa
de Ingeniería de Sonido. Universidad de San Buenaventura Bogotá.
Trabajo de tesis presentado en la universidad de San Buenaventura en el programa de ingeniería de Sonido
en el año 2006. Se realiza un estudio de un instrumento de viento por medio de una simulación 3D aplicando
el método de elementos finitos y algunas otras mediciones experimentales para obtener características de
patrón polar y de respuesta al impulso. En el documento se describe el procedimiento para llevar a cabo el
modelamiento por computadora el cual fue realizado usando el software ANSYS. Se explican los pasos a
tener en cuenta para llevar a cabo el análisis de elementos finitos, de manera que una vez realizados los
modelos en alguna herramienta CAD se definen entradas y salidas del aire, se definen parámetros de
presión y finalmente se realiza la simulación para visualizar los resultados mediante una línea de fluido que
indica el comportamiento de la presión a través de la gaita.
El uso del método de elementos finitos permitió a los autores conocer los puntos de mayor concentración de
energía en el cuerpo de la gaita, así como los puntos en donde se produce menor energía
Se considera que el trabajo se torna relevante para este estudio ya que se habla sobre pasos a tener en
cuenta para la simulación y demuestra que los resultados obtenidos permiten conocer de manera eficaz el
comportamiento energético dentro de un instrumento musical.
The Physics of Musical Intruments. Neville H. Fletcher y Thomas D. Rossing. Second Edition.
Editorial Springer.
Libro especializado en Acústica Musical escrito en el año 1998.Se hace un estudio verdaderamente profundo
sobre una gran cantidad de instrumentos musicales según su clasificación, construcción y ejecución;
haciendo énfasis en su comportamiento matemático, físico y acústico.
Se presenta a la guitarra como un sistema de vibradores acoplados, en donde las cuerdas irradian una
energía casi nula, sin embargo, éstas excitan el puente y la tapa superior, la cual transfiere energía a la
cavidad de aire y a la tapa trasera, de esta forma, el sonido es irradiado de manera eficiente por las tapas
vibrantes y el orificio central. A frecuencia baja, la energía es irradiada como se explicó anteriormente, por
otro lado, a frecuencia alta la energía se irradia principalmente por el puente a través de la tapa frontal.
Se explica que los modos de vibración en la tapa frontal varían cuando se le agrega el varillaje, y cuando la
misma se encuentra con los bordes libres, con un soporte simple, o con los bordes sujetados durante la
medición; observando que se presentan cambios en cuanto a las distribuciones y frecuencias modales. Se
presentan resultados y graficas de mediciones realizadas por varios autores probando que efectivamente
existe variación entre uno y otro caso y diferentes modelos de guitarra, sin embargo, no se explica el detalle
del procedimiento de la medición, ni tampoco el sistema usado para inyectar energía, señal de estímulo,
condiciones de frontera de las tapas (bordes), ni el ambiente acústico de la medición.
1.2 DESCRIPCIÓN Y FORMULACIÓN DEL PROBLEMA
Diversos luthiers que se dedican a la fabricación de guitarras concuerdan que en el diseño de su tapa
convergen detalles vitales para la sonoridad del instrumento que determinan la calidad de una guitarra.
Dichos detalles se aprecian al lograr una eficiencia en tonos brillantes y sobreagudos, así mismo una
agradable resonancia en frecuencias bajas y que la duración de las notas pulsadas sea prolongada.
A lo largo de la historia han sobresalido una cantidad apreciable de diseños de tapas que marcan su
diferencia mediante la distribución y número de varillaje, sin embargo la información que caracteriza estos
diseños no permite conocer si los mismos se realizan bajo un estudio ingenieril previo.
Por tanto, esta investigación se centra en caracterizar y diferenciar el comportamiento acústico de tres tapas
que divergen en su diseño mediante mediciones acústicas y análisis teórico. Por consiguiente, la formulación
del problema está en responder a la pregunta, ¿Qué influencia tiene el diseño del varillaje en el
comportamiento modal de la tapa armónica?
1.3 JUSTIFICACIÓN
El sonido de un instrumento musical que utilice una caja acústica para su resonancia, depende, en
proporciones considerables, del comportamiento de las vibraciones en su cuerpo, por tanto, es útil para
fabricantes e intérpretes conocer este detalle, entendiendo qué es lo que lo hace único en su calidad
tímbrica. Para ello, la acústica musical se especializa en la optimización de las técnicas de construcción
mediante una profundización en su fundamento físico.
Se aplican entonces diferentes técnicas de simulación y experimentación con el fin de observar y analizar
características físico-acústicas de los instrumentos musicales. Para efectos de esta investigación se utiliza
modelamiento por elementos finitos junto a técnicas de generación de patrones modales para analizar la
dinámica vibracional en tapas armónicas de guitarra.
1.4 OBJETIVOS
1.4.1 OBJETIVO GENERAL
Analizar el comportamiento modal de tapas de guitarra según su diseño de varillaje.
1.4.1 OBJETIVOS ESPECÍFICOS
Modelar el comportamiento modal de los diseños escogidos de tapas de guitarra por el método de
elementos finitos.
Determinar la distribución energética en la tapa, mediante la visualización de figuras de Chladni.
Comparar e identificar características que resalten la individualidad de cada diseño.
1.5 ALCANCES Y LIMITACIONES
El proyecto está enfocado en realizar simulaciones usando el método de elementos finitos junto a
mediciones de modos normales de vibración a través de la visualización de patrones de Chladni, para
comparar variaciones en el diseño de varillaje de cuatro tapas armónicas. Los resultados arrojados por la
investigación concederán un mayor entendimiento del comportamiento acústico de una guitarra gracias al
conocimiento de las características de su tapa armónica, respaldando nuevas modificaciones que optimicen
el sistema de construcción de la misma.
El diseño de la tapa frontal de una guitarra acústica varía según la configuración del varillaje, el cual puede
diferir conforme a su cantidad y distribución. Es así como existe una gran diversidad de formas apreciables
en su fabricación, por lo cual la investigación se centra en tres diseños específicos, debido a limitaciones de
tiempo y disponibilidad de los instrumentos. Se escogen las tapas armónicas de la guitarra clásica, flamenca
y folk, que se caracterizan por ser construidas con distintos tipos de madera según su propósito. Por tanto,
también se hace necesario reducir dicha variabilidad a un solo tipo de madera, concentrándose en cambios
estrictamente de varillaje.
Dentro del método experimental de Chladni se inyecta energía a la superficie de manera que las vibraciones
alcancen un estado estacionario. A bajas frecuencias la energía transmitida a la tapa genera vibraciones de
mayor amplitud facilitando la visualización de los patrones modales dentro la medición mientras que en
frecuencias altas, al disminuir la radicación de energía, se dificulta el desplazamiento del material granular
utilizado. En este orden de ideas, se estudiarán los primeros cinco modos de vibración reduciendo el
espectro a frecuencias bajas.
Actualmente se cuenta con múltiples programas computacionales que permiten el proceso de simulación por
elementos finitos, tanto libres como no libres. Sin embargo, para efectos de la investigación se utiliza
únicamente el software ANSYS, cuya licencia está disponible en la universidad.
2. MARCO DE REFERENCIA
2.1 MARCO TEÓRICO CONCEPTUAL
2.1.1 La guitarra
La guitarra está dentro de la clasificación organológica de los instrumentos cordófonos, estos producen el
sonido por una cuerda tensa que entra en vibración activada por medio de la percusión, el pulso o la
frotación con arco. Así mismo, estos instrumentos se dividen en cuatro familias básicas, perteneciendo la
guitarra a la familia del Laúd, donde las cuerdas discurren en paralelo respecto de la tabla armónica y tienen
funcionalmente su misma longitud.
La guitarra, como se conoce hoy en día, se originó en España. Ésta surge en la época renacentista con 4
pares de cuerdas y fue evolucionando hasta convertirse, en el siglo XIX, en un instrumento de 6 cuerdas
simples y una caja de resonancia de mayor tamaño, para dar cabida así mismo a un mayor sonido.
Durante el siglo XVI, la guitarra fue el instrumento popular que tocaban las personas de clase baja,
conviviendo con un instrumento muy similar preferido por la clase aristocrática, la vihuela. Así, mientras los
músicos cultivados en las enseñanzas y tradiciones musicales escribían grandes obras para vihuela, los
músicos aficionados y autodidactas de clases humildes acompañaban con sus guitarras canciones
populares en fiestas. Este período se caracterizó por ser el siglo de oro de la vihuela mientras que la guitarra
se vio bastante marginada.
Tuvo que llegar el siglo XVIII y el gran talento y maestría de guitarristas como Fernando Sor y Francisco
Tárrega, junto a las innovaciones del luthier Antonio Torres para que la guitarra tuviese su gran momento de
esplendor musical. El desarrollo de las primeras guitarras clásicas incluyó el uso de costillas en la tapa
armónica que reforzaron su estructura y permitieron disminuir el grosor de la tapa, adicionalmente se reforzó
el diapasón usando ébano o palisandro y se sustituyó el clavijero de madera por uno de tornillos. 1
Sin embargo, el aporte de Antonio Torres es considerado el mayor de su historia. Fue él quien mejoró los
soportes de la tapa armónica creando el actual abanico, aumentó la caja de resonancia y el ancho del mástil
logrando mejor respuesta en frecuencias bajas y en el volumen del sonido. Este gran resurgimiento se sitúa
en España y tuvo gran proyección internacional gracias a guitarristas como Miquel Llobet, Andrés Segovia,
Regino Sainz de la Maza y Narciso Yepes.
2.1.2 La tapa armónica
De la tapa armónica depende directamente el sonido y la respuesta armónica que dará el instrumento, por lo
que es considerada el elemento principal de la guitarra. Mediante las vibraciones que transmite a través del
puente dentro de la caja de resonancia permite la amplificación del sonido, por ello es de vital importancia
considerar ciertos parámetros en su construcción, tales como simetría, módulo elástico, corte de madera,
entre otros, que determinarán a su vez su riqueza tímbrica.
El rendimiento de la tapa está condicionado por su grosor (el cual puede variar entre 2,5 mm y 4 mm), el tipo
de madera y el diseño de barras de refuerzo. Su fabricación puede darse en diferentes tipos de madera,
preferiblemente aquellas denominadas blandas como ciprés, abeto alemán, cedro canadiense y pinabete,
las cuales garantizan una alta relación de rigidez y densidad. La elaboración de la tapa consta de dos
1
FÁBREGAS IBAÑEZ, Luis. La construcción de la guitarra española. Escuela Suiza de Barcelona. España. 2012, p. 9
láminas obtenidas del corte tangencial de la misma tabla y unidas a la testa en el sentido longitudinal de la
fibra de la madera, asegurando simetría en la disposición de la veta y así mismo obteniendo un equilibrio
acústico.2
Figura 1. Corte de láminas de madera
Imagen tomada de:www.help.solidworks.com/2010/spanish/SolidWorks/cosmosxpresshelp /AllContent/SolidWorks
/NonCore/SimulationXpress/ c_Orthotropic_Material.html. Editada en ordenador para el desarrollo de este documento.
En el tercio superior de la tapa se ubica un agujero que oscila entre los 80 y 95 mm de diámetro y permite
entrar y salir el aire contenido en la caja de resonancia. Su principal objetivo es facilitar la propagación del
sonido del instrumento, de no existir, el aire tendría que comprimirse ante las vibraciones de la tapa
armónica, originando así una amortiguación que imposibilitaría la vibración. 3
La parte posterior de la tapa armónica está formada por un conjunto de varillas de madera clasificadas en
dos tipos, en primer lugar están las barras dispuestas en el sentido de la veta, conocidas como barras
armónicas, que proporcionan masa a la tapa armónica para conseguir resonancia con las frecuencias
emitidas por el vibrar de las cuerdas. También se encuentran las barras transversales situadas en sentido
horizontal, colocando dos encima y una debajo de la boca, para brindar resistencia a la caja de resonancia.
Figura 2. Diseño de varillaje
Imagen tomada de: www.elreparadordeguitarras.blogspot.com
2
3
Fecha de acceso: 26 junio de 2014. <http://www.violeroimaginario.blogspot.com/2011/03/la-guitarra-al-milimetro.html >.
Fecha de acceso: 26 junio de 2014. <http://www.laguitarra-blog.com/2011/02/08/la-tapa-armonica-en-la-guitarra-clasica/>.
2.1.3 Modos normales de vibración
Los modos normales de vibración también reciben el nombre de frecuencias naturales o frecuencias
resonantes, y constituyen los posibles movimientos armónicos que se generan en un sistema en condiciones
de excitación nula. Cada estructura se compone de un conjunto único de estas frecuencias, las cuales
forman un parámetro modal esencial dentro del sistema y dependen únicamente de su rigidez e inercia.
Independientemente de las condiciones iniciales y del tiempo, el sistema tendrá siempre las mismas
frecuencias de resonancia.
El análisis de modos de vibración se define como el proceso de descripción de las propiedades dinámicas de
una estructura elástica en función de los modos normales de vibración. El análisis modal teórico forma parte
de la teoría clásica de vibraciones, éste explica la existencia de frecuencias naturales, de factores de
amortiguamiento y de formas modales de vibración, tanto reales como complejas para sistemas lineales. 4
2.1.4 Materiales elásticos
Los materiales elásticos son aquellos que tienen la capacidad de recuperar total o parcialmente su forma y
tamaño inicial cuando cesa el esfuerzo que había determinado su deformación. Sin embargo, si esta fuerza
externa supera un determinado valor el material puede quedar deformado permanentemente. El máximo
esfuerzo que un material puede soportar antes de este punto se denomina Límite de Elasticidad.
El esfuerzo σ se define como la fuerza por unidad de área:
𝜎=
𝐹
𝐴
Donde, F es la fuerza aplicada y A es el área del cuerpo.
En el sistema internacional el esfuerzo o tensión se mide en[N/m 2], denominado Pascal [Pa].
La deformación ε es el cociente entre la variación de longitud producida por la tensión en una dirección y su
longitud antes de ser sometido a la tensión:
∆𝑙
𝜀=
𝑙𝑜
Donde, ∆𝑙 es el incremento de longitud y 𝑙𝑜 es la longitud inicial.
La deformación es un parámetro adimensional.5
La relación entre esfuerzo y deformación se conoce como módulo de elasticidad. Mientras mayor sea el
valor del módulo más rígido es el material, a su vez los materiales con valores bajos son más fáciles de
doblar bajo carga. El módulo de elasticidad, así como el límite de elasticidad, está determinado por la
estructura molecular del material, las distancias moleculares cambian cuando se crea una tensión en su
interior.
4
JIMÉNEZ BASCONES, J. M. Elementos de máquinas y vibraciones. Departamento de ingeniería mecánica, energética y de
materiales. Universidad Pública de Navarra. España, cap. 2, p. 7
5
Fecha de acceso: 26 junio de 2014. < http://www.ehu.es/rperez/Fisicabio/docs/Propiedades_elasticas.pdf>.
2.1.5 Módulo de Young (Módulo de elasticidad longitudinal)
El módulo de Young estima el estiramiento o la compresión de un objeto, siempre que la fuerza no
sobrepase el límite elástico del material. En la figura 3 se representa el esfuerzo en función de la
deformación unitaria para un sólido. Se denomina comportamiento elástico a la región donde el esfuerzo es
proporcional a la deformación unitaria, caracterizándose porque el material vuelve a su longitud inicial al
disminuir el esfuerzo y cuyo límite se conoce como límite elástico. La siguiente región es conocida como
deformación plástica, en la cual el cuerpo resulta con una deformación permanente. Finalmente, a medida
que sigue aumentando la tensión el cuerpo adquiere una deformación de rotura.6
Figura 3. Gráfica de esfuerzo en función de la deformación unitaria para un sólido.
Imagen tomada de: www.sc.ehu.es/sbweb/fisica/solido/din_rotacion/alargamiento/alargamiento.htm
El módulo de Young (E) es la razón entre el incremento de tensión y el cambio correspondiente a la
deformación unitaria, al igual que el límite elástico, es diferente para los diversos materiales.
𝐸=
𝜎
𝜖
Donde, E es el módulo de Young, σ es el esfuerzo ejercido sobre el área transversal del objeto y ε es la
deformación unitaria en cualquier punto del objeto. En el sistema internacional el módulo de Young se mide
en Pascal [Pa].7
6
7
Fecha de acceso: 26 junio de 2014. < http://www.sc.ehu.es/sbweb/fisica/solido/din_rotacion/alargamiento/alargamiento.htm>.
Fecha de acceso: 26 junio de 2014. < http://www.ehu.es/rperez/Fisicabio/docs/Propiedades_elasticas.pdf>.
Fuerza
aplicada
Deformación
Figura 4. Módulo de Young.
Imagen realizada en ordenador para el desarrollo de este documento.
Está asociado directamente con los cambios de longitud por esa razón se le llama también módulo elástico
longitudinal.
2.1.6 Módulo de Cizalladura (Módulo de elasticidad transversal)
La deformación por cizalladura se produce cuando las fuerzas F que se aplican son tangenciales a una
superficie A, el cambio que se produce en el cuerpo es solo un cambio de forma ya que el volumen
permanece constante (ver Figura 5).Ésta se produce sólo en los sólidos puesto que pueden tener
deformaciones volumétricas y de forma, mientras que los fluidos sólo tienen deformación volumétrica.
Figura 5. Deformación que presenta un objeto al aplicarle una fuerza
Imagen tomada de: www.ehu.es/rperez/Fisicabio/docs/Propiedades_elasticas.pdf
La deformación en cizalla viene dado por el ángulo θ, como se muestra en la figura 5. Para deformaciones
despreciables derivadas de tensiones mínimas dentro de un comportamiento elástico, se tiene:
θ ≈ tan 𝜃 =
∆𝑥
ℎ
El esfuerzo de cizalla está relacionado con la siguiente fórmula:
𝜏 = 𝐺𝜃
Donde, 𝜏 es la tensión o esfuerzo de cizalla, G es el módulo de cizalla cortante y θ es el ángulo de
deformación. Siendo 𝜏 a su vez la razón entre la Fuerza F y el área del cuerpo A. Las unidades del esfuerzo
de cizalla o esfuerzo cortante son [Pa] en el sistema internacional. 8
Fuerza
aplicada
Figura 6. Módulo de Cizalladura
Imagen realizada en ordenador para el desarrollo de este documento.
Este módulo recibe una gran variedad de nombres: módulo de rigidez transversal, módulo de corte, módulo
de cortadura, módulo elástico tangencial y módulo de elasticidad transversal.
2.1.7 Coeficiente de Poisson
Cualquier elemento expuesto a una carga axial experimenta una deformación no solo en el sentido de la
tensión sino también según el eje perpendicular. Es decir, cuando un objeto se estira longitudinalmente, se
comprime en las direcciones perpendiculares al estiramiento. Ver figura 7.
Figura 7. Relación de Poisson
Imagen realizada en ordenador para el desarrollo de este documento.
8
Fecha de acceso: 26 junio de 2014. < http://www.ehu.es/rperez/Fisicabio/docs/Propiedades_elasticas.pdf>.
El coeficiente de Poisson es entonces, la razón entre el estiramiento longitudinal y la reducción deleje
perpendicular a la dirección de la carga aplicada. La fórmula usual para su cálculo relaciona el cociente de
deformaciones:9
𝝂=−
𝜺𝒕𝒓𝒂𝒏𝒔
𝜺𝒍𝒐𝒏𝒈
Donde, v es el coeficiente de Poisson y ε es la deformación. Este coeficiente es adimensional.
Esta constante relaciona el módulo de rigidez y el módulo de Young mediante la siguiente ecuación válida
únicamente dentro del límite elástico del material.
𝐸 = 2𝐺(𝑟 + 1)
Donde, E es el módulo de Young, G es el módulo de rigidez y r es el coeficiente de Poisson.
2.1.8 Materiales ortotrópicos
En un material ortotrópico, las propiedades mecánicas no tienen el mismo valor en todas las direcciones por
lo que sólo se tienen en cuenta tres direcciones perpendiculares e independientes entre sí: longitudinal,
radial y tangencial. Dentro de este tipo de materiales se encuentra la madera, la mayoría de cristales y los
metales laminados. En el caso de la madera, el eje longitudinal es paralelo a la dirección del grano, el eje
radial sigue la dirección de los anillos de crecimiento y el tercer eje es tangente a los anillos de crecimiento. 10
Figura 8. Ejes perpendiculares en la madera. 1. Eje longitudinal. 2. Eje radial. 3. Eje tangencial.
Imagen tomada de: www.help.solidworks.com/2010/spanish/SolidWorks/cosmosxpresshelp /AllContent/SolidWorks
/NonCore/SimulationXpress/c_Orthotropic_Material.html
2.1.9 Método de elementos finitos (MEF).
El método de elementos finitos constituye un avance en la solución de problemas físicos superando las
limitaciones que condicionaban a los métodos matemáticos tradicionales, disminuyendo costos y tiempo de
desarrollo al evitar la experimentación con prototipos que requerían cambios constantes. Partiendo de un
9
ORTIZ BERROCAL, Luis. Elasticidad. Tercera edición. McGRAW-Hill. España. 1998, p.122
SOLÍS RODRIGUEZ, Ernesto. Método de elementos finitos, diseño e ingeniería asistida por computadora. Instituto tecnológico de
Ciudad de Juárez. México. 2013, p. 29
10
sistema completo, este método permite dividirlo en elementos menores de los cuales se obtienen soluciones
que integran la respuesta del modelo completo, de esta forma se puede abordar sistemas cuyo
comportamiento no es posible describir con una sola operación.
El avance de los ordenadores consolidó la vía eficiente para desarrollar las múltiples ecuaciones que plantea
este método, para lo cual se inicia con la construcción de un modelo matemático del sistema real que se
simplificará con su división en un número finito de elementos que se encuentran conectados a través de
nodos. El desplazamiento de estos nodos representa las incógnitas primordiales del problema permitiendo
calcular las incógnitas restantes, tales como tensiones o deformaciones, entre otros.11
La fragmentación de la estructura permite transformar el modelo continuo en uno discreto definido por un
sistema de ecuaciones, teniendo infinitos grados de libertad para el primer caso y un número finito en el
segundo. Es por tanto la discretización una aproximación de los valores de una función a partir del
conocimiento de un número determinado y finito de puntos. 12
Los pasos a seguir en el análisis de estructuras mediante el método de elementos finitos son:
a. Modelar el objeto a estudiar, incluyendo características de los materiales que lo compongan.
b. Desarrollar el enmallado del modelo continuo mediante líneas o superficies imaginarias que
establezcan un número de elementos finitos.
c. Definir las condiciones de contorno y cargas mediante un sistema de fuerzas concentradas en los
nodos, para establecer una relación entre fuerzas y desplazamientos.
d. Obtener los desplazamientos en los nodos que definan el estado de deformación del elemento.
e. Presentar los resultados de forma gráfica para su análisis.
2.1.10 Grados de libertad
Esta expresión toma diferentes significados según el contexto donde se emplee, dentro de un sistema
mecánico, los grados de libertad son los parámetros independientes que determinan la posición y la
configuración deformada del sistema. El número de grados de libertad coincide con el número de ecuaciones
necesarias para describir el movimiento.
Para establecer la posición deformada de un sistema continuo se requiere un número infinito de grados de
libertad, por lo que son posibles infinitos modos independientes de deformarse. Este sistema va a necesitar
infinitos parámetros independientes para especificar la posición de cada punto y definir la configuración
deformada. Por esta razón, en la práctica se obtiene una respuesta aproximada mediante un modelo
discretizado, donde la posición deformada queda fijada por un número finitos de grados de libertad. 13
Durante las simulaciones por computador, la resolución de los problemas mecánicos se realiza mediante la
discretización de un problema continuo, es decir, se estipula un modelo matemático con un número de
grados de libertad finito.
11
BELTRÁN, Francisco. Teoría general del método de los elementos finitos. Departamento de mecánica estructural y construcciones
industriales. España. 1999, p. 27
12
CARNICERO, A. Introducción al método de los elementos finitos. Escuela técnica superior de ingeniería, Universidad Pontificia
Comillas. España. 2001, p. 5
13
JIMÉNEZ BASCONES, J. M. Elementos de máquinas y vibraciones. Departamento de ingeniería mecánica, energética y de
materiales. Universidad Pública de Navarra. España, cap. 1, p. 5
2.1.11 Patrones Sonoros de Chladni
Ernst Florenz Friedrich Chladni fue un físico alemán considerado ocasionalmente el fundador de la acústica,
gracias a la observación sistemática de un experimento que dio nacimiento a la acústica moderna. Dicho
experimento consistía en fijar una placa metálica cuadrada de los extremos o del centro, para después
frotarla con el arco de un violín, donde se había esparcido previamente arena finamente granulada. Los
patrones geométricos formados son conocidos hoy en día como "figuras sonoras de Chladni".
Al vibrar las superficies, las ondas estacionarias generadas producen zonas de máximo desplazamiento
provocando que el material granular se desplace por efecto gravitatorio hacia las zonas de vibración mínima,
pudiéndose visualizar las líneas nodales, es decir, el modo de vibración. En este efecto estacionario las
zonas de amplitud máxima de vibración reciben el nombre de vientres, mientras que aquellas de vibración
nula o mínima se denominan nodos. Para cada frecuencia de resonancia se forma un patrón diferente en la
membrana vibratoria, presentando simetría alrededor del eje central de la misma.14
Figura 9. Registros de Ernst Chladni de patrones modales en placas cuadradas
Imagen tomada de: www.cienciaeingenieria.com/2012/06/re-el-sonido-puede-verse-figuras-de.html
El uso de esta técnica es una aproximación que solo recoge la observación del fenómeno, clasificando las
figuras obtenidas sin explicación. No obstante, la científica francesa Sophie Germain logró modelar
matemáticamente el fenómeno.
14
ELEJABARRIETA OLABARRI, Jesús. El análisis modal: su aplicación a la acústica musical. Bilbao, EuskoIkaskuntza - Sociedad de
Estudios Vascos. 1997, p. 7
3. METODOLOGIA
3.1 ENFOQUE DE LA INVESTIGACION
La investigación implementa pruebas experimentales de medición, análisis y respectivas interpretaciones del
comportamiento modal de la tapa armónica de la guitarra, junto a simulaciones por elementos finitos. Por
tanto el enfoque del proyecto es empírico-analítico.
3.2 LÍNEA DE INVESTIGACION, SUBLINEA Y CAMPO TEMATICO
La línea de investigación de la Universidad de San Buenaventura a la cual pertenece esta investigación es
Tecnologías Actuales y Sociedad, ya que el trabajo se proyecta en un análisis ingenieril sobre el
comportamiento físico-acústico de un instrumento musical.
El trabajo se enfoca en la sublínea de la facultad de ingeniería llamada Análisis y Procesamiento de Señales,
pues los datos que se obtendrán de las respectivas mediciones serán patrones de energía que serán
procesados y analizados para determinar las características modales de la tapa.
El campo temático del programa de sonido en el que se desarrolla el proyecto es Acústica, puesto que se
analizará el comportamiento acústico del instrumento.
3.3 TÉCNICAS DE RECOLECCION DE INFORMACIÓN
Debido a que no existen métodos puntuales ni normas que regulen la medición y análisis de instrumentos
musicales, no se puede hablar de una técnica de recolección de información específica, sin embargo dentro
del desarrollo ingenieril de la investigación está el planteamiento de una técnica de medición adecuada para
el análisis de la tapa de la guitarra.
3.4 HIPÓTESIS
El comportamiento modal en las tapas armónicas de guitarra es completamente dependiente del número y
distribución de barras. Las figuras modales de cada diseño junto con su frecuencia de resonancia se verán
reflejadas en los resultados de la simulación siendo coherentes con la visualización experimental.
3.5 VARIABLES
3.5.1 VARIABLES INDEPENDIENTES
Condiciones del clima como temperatura y humedad
Las mediciones no se llevarán a cabo en una cámara anecoica.
3.5.2 VARIABLES DEPENDIENTES
El tipo de madera
El grosor de la tapa
El número de varillas utilizadas
El diseño del varillaje
El tiempo de secado del barniz
4. PRESENTACIÓN Y ANÁLISIS DE LOS RESULTADOS
4.1 Características de las tapa a estudiar
Para el desarrollo de la investigación se utilizan cuatro tapas armónicas, de las cuales tres contienen diseños
de varillaje específicos y una no contiene ningún tipo de refuerzo. Los tres diseños que se utilizan son los
aplicados en guitarras folk, guitarras clásicas y guitarras flamencas. Habitualmente este tipo de guitarras no
sólo difieren en el diseño de sus barras sino también por tener geometrías y materiales distintos, siendo la
guitarra folk la de mayor tamaño seguida de la guitarra clásica y por último la guitarra flamenca.
La guitarra clásica moderna fue desarrollada por Antonio Torres en España durante el siglo XIX, quien
diseñó una guitarra de caja grande, implementándole a la tapa siete costillas dispuestas en forma de abanico
para obtener un mayor volumen y respuesta tonal. Su trabajo representó uno de los avances más
importantes en la historia de la construcción de guitarras y casi todos los instrumentos convencionales
actuales se derivan de su trabajo. Generalmente se utiliza madera palosanto para los aros y el fondo de la
guitarra, mientras que para la tapa suelen usarse dos tipos de madera, el abeto y el cetro.
La guitarra flamenca cuenta con aros más estrechos y disposición de cuerdas más cercana al mástil debido
a la altura del puente y al ángulo que se presenta entre el aro, la tapa y el mástil. La tapa es más delgada y
todo el instrumento es más ligero que una guitarra clásica. En la mayoría de los casos este tipo de guitarras
implementan una protección en sus cajas sonoras cerca de la zona aguda de las cuerdas usualmente de
plástico o de caparazón de tortuga conocido como “el golpeador”, el cual permite al guitarrista utilizar su
instrumento percutivamente sin deteriorarlo. El tipo de madera usada para los aros y el fondo es Ciprés
macizo español y para la tapa Abeto Alemán.
La guitarra folk, por su lado, tiene una caja de resonancia de mayor tamaño, las cuerdas utilizadas son de
acero ejerciendo una presión mucho más considerable en el puente. El sistema requirió ciertas
modificaciones para soportar la tensión extra de las cuerdas, en primer lugar el mástil tiene un diseño más
angosto y es más fuerte. Se modifica también el baretaje de la tapa armónica incluyendo un diseño en X,
que consta de dos costillas que se cruzan entre la roseta y el puente, y es capaz de proporcionar solidez y
resistencia a la tapa. De esta forma se logra elevar la eficiencia ofreciendo un equilibrio entre resistencia,
potencia y la libertad de vibración requerida por la caja sonora. La colocación de las costillas secundarias se
determinaba a menudo en forma empírica de modo que la caja expresase su máximo potencial.
Nota: Las tapas a estudiar fueron elaboradas por el lutier bogotano Enrique Rodríguez Galvis, especializado
en la fabricación de guitarras para objeto de esta investigación.
a
b
c
Figura 10. Guitarra a. clásica b. flamenco c. folk
a. Imagen tomada de www.guitarrasbros.com/espanol/guitarras/guitarra-clasica-de-estudio-francisco-bros-B5.php#.U_eHR8V5Muc
b.- c. Imágenes tomadas de www.fender.com/es-CO/acoustics/
El comportamiento de cada guitarra se ve afectado por diversos factores en su diseño como el tamaño de su
caja de resonancia, el tipo de cuerdas y su tensión, el puente, los aros ubicados en la boca, el mástil, el tipo
de madera utilizado en su construcción, la técnica de barnizado, diseño de varillaje, entre otros. Todos estos
parámetros se convierten en variables que afectan el comportamiento modal dentro de cada diseño, no
obstante, al centrarse este estudio en las variaciones dadas por las barras al respaldo de las tapas se omiten
las diferencias de cada estilo de guitarra y se establece un tamaño y material de referencia, de esta manera
se garantiza que los resultados de la investigación estarán condicionados por la disposición de las costillas.
Las superficies a medir están construidas de pino cien hilos con las siguientes dimensiones:
Figura 11. Dimensiones de las tapas
Imagen realizada en ordenador para el desarrollo de este documento.
La primera tapa bajo medición contiene el diseño utilizado en guitarras flamencas que consta principalmente
de siete barras dispuestas en configuración de abanico en la parte más ancha de la tapa y dos más
formando una v en la zona inferior. Adicionalmente se sitúan en la parte superior e inferior de la boca de la
guitarra dos barras dispuestas horizontalmente caracterizadas por tener mayor altura y grosor, y una tercera
barra de menores proporciones se ubica unos centímetros más arriba. Éstas se encargan de soportar la
tensión generada por el mástil. Por último dos refuerzos verticales a los dos lados de la abertura de la tapa,
de menor altura y de un ancho considerable.
La siguiente tapa corresponde a un diseño para guitarras clásicas, el cual es similar al diseño previamente
mencionado, en este caso se utilizan siete barras para el abanico y se eliminan aquellas que forman una v.
Este diseño conserva las barras que sirven de refuerzo para el mástil de la guitarra.
El tercer diseño, implementado en guitarras folk, está constituido por dos barras en forma de X cruzándose
entre sí a 4.5 centímetros debajo de la boca y con una placa de forma trapezoidal bajo su unión. Éstas son
las de mayor longitud por lo cual abarcan una mayor área en la superficie de la tapa y a sus costados se le
adhieren seis costillas de menor altura y longitud. El diseño también cuenta con los soportes destinados a
resistir la carga del mástil.
a.
b.
c.
Figura 12. Diseño de varillaje de las tapas a. Clásica, b. Folk, c. Flamenca
.
Imagen realizada en ordenador para el desarrollo de este documento.
A continuación se muestran las dimensiones de las barras de refuerzo de cada tapa. Nota: Las tapas Clásica
y Flamenca presentan un eje de simetría, por tanto las varillas numeradas 5, 6, 7 y 9 respectivamente tienen
las mismas medidas de las barras reflejadas.
El refuerzo de forma trapezoidal de la tapa folk (4) tiene un largo superior de 3 cm e inferior de 16 cm.
Clásica
Nomenclatura
1
2
3
4
6,7,8
5
largo
(cm)
21,5
26,5
24,5
12,6
22
20,5
ancho
(cm)
1,2
0,7
0,7
3
0,3
0,3
alto (cm)
0,3
1,4
1,6
0,1
0,4
0,4
Tabla 1. Dimensiones varillaje de tapa clásica
Flamenca
Nomenclatura
1
2
3
4
5
6
7
8
9
largo
(cm)
21,5
26,5
24
12,2
22,5
20
18
16
18,5
ancho
(cm)
1,2
0,7
0,7
3,3
0,3
0,3
0,3
0,3
0,3
alto
(cm)
0,3
1,5
1,6
0,1
0,5
0,5
0,5
0,5
0,5
Tabla 2. Dimensiones varillaje de tapa flamenca
Folk
Nomenclatura
1
2
4
3
7
8
5
6
9
10
largo
(cm)
26
10
16
42
9,8
8,2
8,2
7,6
22
22
ancho
(cm)
0,7
1,8
6,5
0,7
0,5
0,5
0,5
0,5
0,5
0,5
alto
(cm)
1,6
0,1
0,2
1,5
0,7
0,7
0,7
0,7
0,7
0,7
Tabla 3. Dimensiones varillaje de tapa flamenca
4.2 Modelamiento de problemas dinámicos por método de elementos finitos
El campo de la mecánica puede ser abordado desde el área teórica, encargada de estudiar las leyes y
principios de la mecánica por su valor científico, el área aplicada donde los conocimientos teóricos se
transfieren a las aplicaciones científicas e ingenieriles y el área numérica para resolver problemas que son
difíciles de desarrollar analíticamente. Las soluciones analíticas son aquellas expresiones matemáticas que
requieren la solución de ecuaciones diferenciales que involucran geometrías complejas, cargas no
distribuidas y determinación de propiedades de los materiales. Gracias a los avances de la computación, el
resultado se puede obtener a partir de la resolución numérica utilizando esta herramienta de apoyo.
El método de elementos finitos permite el cálculo de problemas dinámicos, utilizados en diversas
aplicaciones de la ingeniería, al considerar la estructura como la división de elementos discretos, con
determinadas condiciones de vínculo entre sí. Esto genera un sistema de ecuaciones que se resuelve
numéricamente y proporciona el estado de tensiones y deformaciones. La formulación de este método
permite que el problema sea planteado por una serie de ecuaciones algebraicas simultáneas, evitando la
resolución de ecuaciones diferenciales complejas.
Para el análisis un sistema real, es fundamental determinar un modelo matemático que recoja las
propiedades físicas del modelo real. En el caso particular, de un sistema mecánico estos parámetros son la
rigidez (k), la masa (m) y el amortiguamiento(c). Los cuales se relacionan con la fuerza elástica, la fuerza de
inercia y la fuerza de disipación de energía respectivamente, características de los problemas de
vibraciones.
Dentro de los sistemas físicos reales se incluyen parámetros continuos, es decir, ningún elemento se
concebirá sin masa, o que se deforme sin la aplicación de ninguna fuerza. No obstante, es posible obtener
una aproximación razonable a los modelos matemáticos concentrando en determinados puntos las distintas
características del sistema. Existen así, los parámetros concentrados en los cuales se atribuye a resortes
ideales toda la capacidad de absorción de energía elástica, a masas indeformables toda la energía cinética,
y a amortiguadores viscosos toda la capacidad de disipación de energía, aproximando el comportamiento de
los componentes distribuidos reales bajo ciertas restricciones.
La simulación por el método de elementos finitos permite la discretización de un problema mediante la
reducción de un sistema continuo, en el cual las posiciones deformadas están determinadas por un número
infinito de grados de libertad, a un modelo discreto de parámetros distribuidos, cuyo número de grados de
libertad es finito.
Análisis Modal
En la búsqueda de optimizar las características dinámicas de las estructuras, el incremento de la tecnología
ha desarrollado métodos ingenieriles que crean seguridad y rentabilidad en el diseño de modelos mediante
el conocimiento de su comportamiento vibracional, teniendo innumerables aplicaciones y cubriendo extensas
áreas que abarcan desde la aeronáutica, mecánica e ingeniería civil, hasta la acústica.
El proceso de representación de las propiedades dinámicas de una estructura elástica en función de los
modos normales de vibración es conocido como Análisis Modal. Estos modos son una configuración
deformada en donde cada punto tiene una vibración armónica alrededor de una posición de equilibrio. El
movimiento de este sistema físico es descrito por un conjunto de ecuaciones diferenciales lineales
simultáneas de segundo orden de la forma:
[𝑀]{𝑥}̈ + [𝐶]{𝑥}̇ + [𝐾]{𝑥} = {𝑓(𝑡)}
Donde;
f(t), es el vector de fuerza aplicada.
x(t), el vector resultante del desplazamiento.
M, C y K la matriz de masa, amortiguamiento y rigidez.
Ec (1)
Esta ecuación es discretizada en función de los desplazamientos, velocidades y aceleraciones nodales
permitidos a la estructura.
Sin embargo, los programas de elementos finitos no contemplan el amortiguamiento del sistema para el
cálculo de los modos y frecuencias naturales. De esta manera, la ecuación (1) queda reducida a:
𝑀𝑥̈ (𝑡) + 𝐾𝑥(𝑡) = 𝑓(𝑡)
Ec (2)
La resolución de la ecuación (2) involucra establecer si el sistema está sometido a una vibración libre o
forzada. Al igualar la fuerza a cero, las vibraciones son consideradas libres por lo que no existen fuerzas o
acciones exteriores directamente aplicadas al sistema a lo largo del tiempo. Mientras que en el caso
contrario reciben el nombre de vibraciones forzadas, al existir acciones o excitaciones directamente
administradas al sistema a lo largo del tiempo. Cabe resaltar que dentro de la simulación la aplicación
externa de cargas es igual a cero para las vibraciones libres.
Por tanto, para obtener las frecuencias naturales es necesario sacar al sistema de su posición de equilibrio y
dejarlo en libertad, reduciéndola ecuación a:
𝑀𝑥̈ + 𝐾𝑥 = 0
Ec (3)
Para el caso de F(t)=0. La solución de este sistema de ecuaciones requiere el cálculo de cada valor propio
donde hay n incógnitas más un parámetro, siendo las incógnitas el desplazamiento de cada grado de
libertad y el parámetro adicional la frecuencia de resonancia. El sistema tendrá n ecuaciones de movimiento,
donde los vectores propios son conocidos sólo como relaciones de desplazamientos, y no como magnitudes
absolutas. El sistema tendrá un número infinito de soluciones que son los modos de vibración.
Por el contrario, al definir la Ecuación (2) F(t)≠0, los desplazamientos de los grados de libertad quedan
determinados al tener un sistema con el mismo número de ecuaciones e incógnitas, pues a diferencia del
análisis modal, la frecuencia deja de ser una incógnita. Este tipo de análisis es conocido como análisis
armónico.15
La solución de las vibraciones libres no amortiguadas es una función armónica que oscila con una frecuencia
característica del sistema denominada frecuencia natural (ecuación 4), la cual no depende de condiciones
iniciales ni de tiempo, garantizando que el sistema siempre vibra a la misma frecuencia.
𝑤= √
𝐾
𝑀
15
Ec (4)
TORRES Jesús Alejandro, RUIZ Ricardo. Identificación a simple vista de patrones de vibración de una tapa de guitarra. Universidad Autónoma
de México. México. 2008, p. 3
Figura 13. Respuesta armónica para vibraciones libres no amortiguadas
Imagen tomada de: JIMÉNEZ BASCONES, J. M. Elementos de máquinas y vibraciones. Departamento de ingeniería mecánica,
energética y de materiales. Universidad Pública de Navarra. España, cap. 1, p. 6
Un sistema con n grados de libertad tendrá n frecuencias naturales y n modos naturales de vibración cuando
no actúen cargas exteriores y no hayan términos disipativos, por el contrario, si dentro una vibración forzada
el sistema se somete a una excitación armónica este llegará a la condición de resonancia para n frecuencias
de excitación diferentes. Se precisa de n parámetros o coordenadas para definir la posición y configuración
deformada de estos sistemas, por lo que su estudio requiere la formulación matricial y el uso de las
propiedades del álgebra lineal.
Suponiendo que el sistema con n grados de libertad tiene un comportamiento lineal, se puede resolver
superponiendo n sistemas con un grado de libertad, lo que se conoce como principio de superposición. El
cual consiste en multiplicar los modos de vibración por factores de escala y superponer los para obtener los
desplazamientos ante una excitación. En este orden de ideas, al desplazar el sistema de su posición de
equilibrio según un modo natural y soltarlo, todos los puntos oscilarán libre y armónicamente a la frecuencia
propia del modo.16
4.3 Simulación por elementos finitos
Ansys Multiphysics es un software de simulación numérica por el método de elementos finitos, desarrollado y
comercializado para prestar un soporte a la ingeniería en la predicción del funcionamiento y reacción de un
determinado producto bajo un entorno real. Este programa permite llevar a cabo desde el análisis estático
lineal, el cual ofrece simplemente tensiones y deformaciones, hasta el estudio de fenómenos transitorios no
lineales avanzados que implican efectos dinámicos y comportamientos complejos. Existen en total siete tipos
de análisis estructurales presentes en la familia de productos de Ansys, donde se incluye el análisis modal,
utilizado para calcular frecuencias naturales y formas modales de una estructura determinando así las
características de una vibración.
La escogencia de este programa parte de la fidelidad de los resultados, gracias a que cuenta con una amplia
variedad y calidad de materiales disponibles, tipos de elementos; y robustez en los algoritmos de solución
que permiten modelar cada producto con cientos de componentes interactuando simultáneamente.
Para desarrollar un análisis estructural en Ansys es importante conocer la estructura general del programa,
puesto que consta de tres módulos con una serie de aplicaciones para cada etapa de la simulación donde se
agregan datos específicos y se visualizan resultados respectivamente. Estos módulos son: el preprocesador,
solucionador y post-procesador.
16
JIMÉNEZ BASCONES, J. M. Elementos de máquinas y vibraciones. Departamento de ingeniería mecánica, energética y de
materiales. Universidad Pública de Navarra. España, cap. 5, p. 4
4.3.1 Pre-Proceso
Dentro de la etapa del preprocesador de Ansys APDL se define el tipo de elemento, sus parámetros, y
propiedades del material. Así mismo, se determinan las características relacionadas con el modelamiento de
las geometrías, ya sean en 2D o 3D, y propiedades de la malla. Este es quizás el módulo más importante,
donde se generala malla y quedan establecidas todas las variables que afectan al objeto estudiado,
realizando una aproximación discreta del problema en base a puntos o nodos, los cuales se conectan para
formar el volumen del modelo.
Tipo de elemento
El método de elementos finitos permite analizar estructuras y modelos tridimensionales, sin embargo este
análisis requiere tanto un mayor uso de recursos computacionales como una mayor cantidad de tiempo
comparado con el estudio de un objeto bidimensional.
Dentro de este tipo de elemento se escogió particularmente el elemento Solid 92, el cual es un elemento tipo
sólido estructural tetraédrico definido a partir de diez nodos, con tres grados de libertad cada uno que
corresponden a las tres traslaciones de los ejes X, Y y Z. Los nodos son puntos con que se discretizan los
modelos a analizar y contienen los grados de libertad, es decir, las variables a ser calculadas en la
simulación. Este elemento resulta adecuado para modelar mallas irregulares, soportar deformaciones de
gran tamaño y llevar a cabo un análisis modal. La siguiente figura identifica las caras del elemento y
representa su sistema coordenado.17
Figura 14. Elemento Solid 92
Imagen tomada de: www.mostreal.sk/html/elem_55/chapter4/ES4-92.htm
Propiedades del material
Con el fin de otorgar a la simulación un nivel de semejanza con la realidad es preciso definir los parámetros
físicos de los materiales del objeto estudiado. El menú de propiedades contiene a su vez un submenú donde
se establecen las características necesarias.
El material de las tapas de guitarras es madera tipo pino considerado lineal, elástico y ortotrópico. En cuyo
caso el número de constantes elásticas es 9, para cubrir las tres direcciones de la madera: longitudinal,
tangencial y radial. Las nueve constantes independientes son entonces EL, ET, y ER para los módulos de
Young; GL, GT, y GR para los módulos de cizalla; y VLT, VLR, y VTR para las relaciones de Poisson.
17
ROA GARZÓN, Máximo Alejandro. GARZÓN ALVARADO, Diego Alexander. Introducción al modelamiento por elementos finitos con
ANSYS. Universidad Nacional de Colombia. Colombia. 2002, cap. 9, p. 1
Los valores del tensor elástico del material de las tapas usados en el modelo de elementos finitos están
dados en la Tabla 4.
Material
Pino
EL(GPa)
0.72
ET (GPa)
0.65
ER (GPa)
9.1
VLT
0,037
VLR
0,037
VTR
0,037
GLT(GPa)
1,1
GLR(GPa)
0.6
GTR(GPa)
0.02
Tabla 4. Constantes elásticas de la madera estudiada
Información tomada de: Ezcurra, A. (1996) Influence of the material constants on the low frequency modes of guitar plate. Journal of
Sound and vibrations, 194.
Además, dentro de la simulación se hace necesario especificar la densidad de la madera, la cual indica cuan
comprimido se encuentra un material en un espacio determinado, es decir, la cantidad de masa por unidad
de volumen. Este parámetro varía según el tipo de material, en la tabla 5 se muestran las características
generales del material estudiado.
Material
Pino
Masa (gr)
194
Espesor (mm)
2,5
Densidad (Kg/m3)
572
Tabla 5. Especificaciones físicas del material
Información tomada de: Mcintyre, M. E. and Woodhouse, J. (1986) On measuring wood properties (part. 3). Cambridge University
Engineering Department.
Geometría
La creación de la geometría se hace directamente en Ansys, aunque el software ofrece como alternativa el
diseño de un modelo sólido en un sistema CAD, guardarlo como un archivo IGES, y luego importarlo. Una
vez importado correctamente, se puede enmallar el modelo tal como lo haría para cualquier modelo creado
en el marco del programa.
Gracias a la simetría del objeto estudiado, el proceso para su realización inició con la ubicación de los
puntos del contorno izquierdo y luego su unión mediante líneas, finalmente se completó la figura reflejando el
lado derecho.
Nota: Las figuras 15 a 27 son capturas de pantalla obtenidas de Ansys APDL para el desarrollo de este documento.
Figura 15. Creación de puntos en Ansys APDL
Figura 16. Formación de líneas en Ansys APDL
Figura 17. Función para reflejar la imagen
Una vez hecho el contorno de la tapa se crea el área de la superficie del objeto estudiado, posteriormente se
realiza una circunferencia con el mismo diámetro de la boca de la tapa para sustraer esta nueva área de la
anterior y así obtener la figura real de la tapa.
Figura 18. Área generada en Ansys APDL
Figura 19. Creación de la boca en la tapa
En el caso de la construcción de las barras se usaron bloques que se fueron ubicando a la misma
disposición de las tapas. Es necesario que sus líneas compongan un mismo sólido con el resto de la tapa
para que cuando se apliquen cargas no ocurran fallos en los desplazamientos y en las cargas, razón por la
cual los puntos que pertenecen a las diferentes barras deben ser comunes con el resto del cuerpo.
A continuación se presentan las geometrías involucradas en la simulación, cada figura muestra tres vistas
distintas.
Figura 20.Tapa sin varillaje generada en Ansys APDL
Figura 21. Tapa Clásica en Ansys APDL
Figura 22. Tapa Flamenca en Ansys APDL
Figura 23. Tapa Folk en Ansys APDL
Nota: Para facilitar el modelamiento de la tapa de la guitarra folk, se realizó la suma de cinco barras
horizontales que ocupan el área comprendida originalmente por el trapecio.
Parámetros de malla
Una vez creada la geometría es necesario hacer la malla de elementos finitos, la cual está constituida por
milésimos puntos donde se asignan las fuerzas, flujos térmicos o temperaturas en caso de haberlas. El
programa por defecto puede tomar valores para generarla sin que el usuario altere algún parámetro, sin
embargo dichos valores no resultan ser en todos los casos los más óptimos. Resulta preciso especificar el
tamaño y forma de los elementos que van a conforma la malla.
Es acá donde el problema es discretizado dividiendo el dominio del espacio total en subdominios simples,
llamados elementos. De esta manera el objeto creado será divido mediante líneas en elementos finitos
conectados entre sí por un número discreto de nodos, para problemas tridimensionales es común utilizar
elementos tetraédricos.
La malla consta de una resolución pequeña garantizando la obtención de resultados rigurosos sin interferir
con la capacidad de procesamiento del ordenador, por lo cual en cada modelo se utilizan el número de
elementos que se muestran en la siguiente tabla.
Modelo
Tapa sin barras
Tapa clásica
Tapa flamenca
Tapa folk
Número de elementos
7304
9822
10761
17290
Tabla 6. Número de elementos en cada modelo
A continuación se presenta el enmallado resultante en cada tapa a estudiar, el cual es el paso previo a la
solución modal.
Figura 24. Malla tapa armónica sin varillaje.
Figura 25. Malla tapa armónica clásica
Figura 26. Malla tapa armónica flamenca
Figura 27. Malla tapa armónica folk
4.3.2 Solución
Para continuar con la etapa de solución es indispensable haber establecido el tipo de elemento, las
propiedades del material, el modelo estudiado y los parámetros de la malla. En esta nueva fase se aplican
de las condiciones de contorno junto con la carga, donde se especifica las restricciones de los
desplazamientos y las fuerzas y temperaturas aplicadas en los nodos.
Por último se debe escoger el tipo de análisis pertinente en cada estudio para dar inicio al cálculo. Ansys
ofrece 7 tipos de análisis estructurales diferentes: análisis estático, análisis modal, análisis armónico, análisis
dinámico, análisis de espectro, análisis del pandeo y análisis explícito dinámico.
Condiciones de contorno y carga
El objetivo al realizar este análisis de elementos finitos es estudiar cómo las cuatro tapas escogidas
responden a ciertas condiciones de carga, por lo cual resulta un paso clave determinarlas apropiadamente.
Dentro de la simulación, este módulo incluye las condiciones de frontera y las fuerzas aplicadas interna o
externamente al modelo.
Existen dos casos para establecer las condiciones de frontera dentro de un estudio, el primero denominado
libre se aplica a estructuras que no tienen restricciones en movimientos de traslación ni de rotación, y el
segundo para condiciones de frontera fijas permite restringir el movimiento de la estructura en ciertas o todas
las direcciones y rotaciones. Para efectos de esta investigación se fijó todo el borde de cada tapa como si
estuviera ensamblada con el resto de la caja pero sin el brazo, con el fin de evitar que la tapa pudiera tener
movimientos de traslación en alguna dirección y llevando el estudio a condiciones de funcionamiento real.
Contorno con
desplazamiento
restringido
Zona con
desplazamiento
libre
Figura 28.Condiciones de frontera
Imagen realizada en ordenador para el desarrollo de este documento.
La simulación de las tapas de guitarra estudia su comportamiento natural condicionándose exclusivamente
en la geometría y propiedades del material, sin inyectarle ninguna fuerza externa. Por tanto en éste módulo
no se establecerá ningún tipo de fuerza al modelo, llevar a cabo un análisis modal no requiere cargas.
Tipo de análisis
El paso restante para dar inicio a la solución del problema es indicar el tipo de análisis requerido. Dado que
el objetivo de este estudio es calcular frecuencias naturales y formas modales de cada uno de los cuatro
diseños de tapas se selecciona el análisis modal, en donde tanto las frecuencias naturales de vibración de
una estructura como los modos principales de vibración dependen únicamente de la geometría, los
materiales y la configuración de la estructura.
Dentro del análisis modal debe definirse la cantidad de modos normales a simular. A bajas frecuencias la
energía transmitida a la tapa genera vibraciones de mayor amplitud, favoreciendo el modo más bajo de
vibración y facilitando la visualización de las figuras modales en la superficie dentro de la medición
experimental. En frecuencias superiores a 1000 Hz disminuye la radiación de energía, por lo que las áreas
de vibración son más pequeñas, dificultando el estudio por los métodos usados en esta investigación.18
Se determina que la simulación entregue en sus resultados hasta cinco modos de vibración. Cada modo se
muestra en términos de sus parámetros modales: frecuencias naturales y características de patrones de
desplazamiento. En el análisis modal, el software Ansys APDL no tiene en cuenta el valor de amortiguación,
por lo cual no se considera.
4.3.3 Post-Proceso
En la etapa de post-proceso se visualizan los resultados obtenidos a través de representaciones gráficas y
listas con los parámetros estudiados que permiten al usuario extraer conclusiones del problema. El software
entrega el comportamiento del objeto a estudiar, para este caso, muestra las figuras modales con una escala
de colores según los puntos de concentración de mayor energía. Dentro la interfaz gráfica de usuario se
muestran datos correspondientes a la frecuencia, número de modo, valores de máximos de esfuerzo y
desplazamiento.
A continuación se muestra la captura de pantalla de la interfaz gráfica de Ansys APDL al suministrar los
resultados. Con el fin de facilitar su interpretación se explica posteriormente los datos allí listados.
Figura 29.Interfaz gráfica de resultados
Captura de pantalla obtenida de Ansys APDL para el desarrollo de este documento
18
GONZALEZ, Esteban. Primera aproximación a la acústica de la guitarra. Buenos Aires, Argentina. 2012, p. 2
En la esquina superior izquierda de cada imagen se listan los siguientes datos:
NODAL SOLUTION- Tipo de solución desarrollada en la pantalla.
STEP= - Paso de carga del análisis
SUB= -Número del modo de vibración
FREQ= -Frecuencia en HZ
USUM (AVG) –Tipo de resultados graficados en la pantalla. Combinación de los esfuerzos en la
dirección X, Y y Z.
RSYS= -Sistema de coordenadas para la visualización de los resultados.
DMX= -Valor de máximo desplazamiento en mm.
SMX= -Valor de máxima deformación en mm.
La franja de nueve colores ubicada en la parte inferior representa un código que indica el desplazamiento de
diferentes zonas de la tapa, el color azul corresponde al valor mínimo mientras el color rojo al máximo.
Dentro del análisis modal de una estructura los valores obtenidos coinciden con el comportamiento de la
pieza con valores imaginarios por lo que los desplazamientos no representan magnitudes absolutas. De esta
manera, estos datos son irrelevantes dentro de este estudio puesto que el enfoque está en comparar
frecuencias de resonancia y figuras resultantes de modos de vibración.
4.4 Visualización de Figuras Chladni
4.4.1 Esquema de medición
Para las mediciones experimentales se resuelve diseñar un soporte que sujete las placas por el borde
simulando las condiciones de frontera reales que se dan en una tapa fijada al cuerpo de la guitarra. El
soporte se eleva a 45 cm de altura y consta de dos láminas de mdf de 1 cm de grosor cada una cubiertas de
moqueta y aseguradas con cuatro tornillos pasantes que permiten graduar la fuerza con la cual la tapa se
aferra.
Nota: Las figuras 30, 31, 32 y 34 son fotografías realizadas para el desarrollo de este documento.
Figura 30. Soporte para las tapas
Posteriormente, se ubica un parlante bajo el soporte que sirve como excitador mecánico con el que se
inyecta una señal y fuerza conocida al instrumento en estudio. Para lograr una transmisión de energía
directa o de contacto se modifica el altavoz reemplazando el diafragma por un cilindro de diámetro 3,8 cm y
altura 7,2 cm. Para su ubicación se diseña una base que suspenda el altavoz a una altura constante y
garantice que sus extremos estén desacoplados, de manera que el cilindro golpee la superficie en la zona
del puente en la cara anterior de las tapas.
Figura 31. Parlante utilizado en las mediciones
Figura 32. Soporte para parlante
La señal que alimenta todo el sistema experimental parte desde un generador de ondas que a su vez se
mantiene monitoreado mediante un osciloscopio. Dicha señal es dirigida a un amplificador de potencia para
elevar el nivel de línea a nivel de altavoz.
Generador de
ondas
Soporte tapa
Superficie a medir
Amplificador
Osciloscopio
Transductor
Soporte transductor
Figura 33. Esquema de medición
Imagen realizada en ordenador para el desarrollo de este documento.
Finalmente, para la generación de figuras Chladni se escogió sal de cocina como material granular y fue
esparcida de manera homogénea sobre la superficie de la tapa a medir.
Figura 34. Superficie con sal de cocina
Para las mediciones experimentales se toman las siguientes recomendaciones:
La medición se debe llevar a cabo en lo posible en un ambiente seco para evitar la formación de
grumos en el material granular
La placa bajo medición se debe ubicar de modo completamente horizontal, garantizando que las figuras
formadas por el material granular se deban a la distribución de energía mas no por la fuerza gravedad.
El material granular debe ser previamente distribuido de forma homogénea sobre la superficie evitando
usar las manos, ya que la grasa de la piel puede formar grumos. Para ello utilizar alguna herramienta de
bordes planos. Redistribuir el material para encontrar nuevos modos.
El diseño del soporte debe tener un punto mínimo de contacto para no generar mayor perturbación en la
vibración natural de la placa
4.4.2 Medición del parlante
Se realiza una medición fundamentada en los parámetros Thiele – Small en el transductor utilizado como
excitador mecánico, cabe resaltar que debido a la sustitución del cono por un cilindro, se omiten las
mediciones mecánicas que involucren interacción del diafragma y se enfoca en parámetros eléctricos. Para
ello, se obtienen diferencias de potenciales sobre la resistencia del parlante variando la frecuencia y se
tabula los datos obtenidos.
Para el montaje de la medición se utiliza un generador de ondas conectado a una resistencia de carga RL, la
cual forma un circuito en serie con la resistencia del parlante R E. Los valores de las resistencias fueron de
0.991 KΩ y 7.6 Ω respectivamente. Se inyecta una señal sinusoidal al circuito de frecuencia y amplitud
conocida, y con el uso de un multímetro se toman los voltajes generados en ambas cargas. Posteriormente
se varía la frecuencia de la señal y se repite el proceso conservando una amplitud de 2 voltios.
RE
Amplificador
RL
Generador de
Frecuencias
CH 1
CH 2
Multímetro
Figura 35. Esquema de medición del transductor
Imagen realizada en ordenador para el desarrollo de este documento.
Figura 36. Montaje de medición del transductor
Fotografía realizada para el desarrollo de este documento.
A continuación se muestran los resultados promediados de tres mediciones por frecuencia sobre el
transductor, se tomaron frecuencias desde 30 a 250 Hz con un paso entre cada muestra de 10 Hz.
Los resultados de la medición muestran que el parlante presenta ligeras variaciones de amplitud y con
resonancia en 130 Hz, apreciándose una diferencia menor a 1 mV con respecto a los demás datos de la
gráfica. Éste valor no representa un cambio significativo, por tanto no es necesario hacer ajustes de
atenuación o ganancia a la señal que alimenta el transductor para las mediciones de patrones de Chladni,
garantizando que la influencia del parlante sobre las mediciones será mínima.
mV
12
10
Medición de Parlante
Respuesta en
frecuencia
8
6
4
2
0
30 40 50 60 70 80 90 100110120130140150160170180190200210220230240250
Figura 37. Gráfica de respuesta en frecuencia del transductor.
Gráfica realizada en ordenador para el desarrollo de este documento.
Hz
5. ANÁLISIS DE RESULTADOS
5.1 Simulación por elementos finitos
El comportamiento modal de cada tapa se presenta a través de cinco imágenes, una por cada modo de
vibración indicando su frecuencia de resonancia y agrupadas según el diseño de cada tapa armónica.
Nota: Con el fin de proporcionar una visualización general de las figuras y facilitar la comparación entre cada
modo y diseño, se realiza una reducción el tamaño de las capturas de pantalla (figuras 38 a 41) obtenidas de
Ansys APDL. No obstante, se pueden observar a mayor escala y con la información proporcionada por el
programa en la sección de anexos de este documento.
52.6 Hz
89.06 Hz
109.8 Hz
128.1 Hz
174.03 Hz
Figura 38. Modos de vibración por elementos finitos. Tapa armónica sin varillaje.
Debido a que los valores de desplazamiento arrojados por la simulación no se consideran dentro de este
estudio se realizará un análisis cualitativo de las figuras modales que presenta cada tapa, por lo que el único
valor numérico a tener en cuenta es la frecuencia propia de cada modo.
Modo 1: La mayor cantidad de energía coincide con la ubicación del puente, el cual inicia la transmisión de
energía al resto de la superficie cuando el ejecutante pulsa las cuerdas. La distribución modal es uniforme
hacia el borde de la tapa, generando su mínimo valor en esa zona.
Modo 2: La parte superior de la placa presenta la región de mayor concentración de energía, rodeando la
boca con el máximo valor, mientras que en la zona más amplia de la tapa se forma un cúmulo con un nivel
energético inferior.
Modo 3: Sobre la tapa se evidencian dos zonas con una distribución uniforme a lo largo de la superficie
consiguiendo ambas un valor de energía máximo. Gracias a la simetría de la placa, el comportamiento
modal es equivalente entra ambas regiones.
Modo 4:Se forman tres regiones de concentración de energía, cuyo máximo valor se presenta en la zona
superior a la boca de la guitarra de manera similar al segundo modo. Las zonas restantes se distribuyen en
la parte media e inferior de la tapa disminuyendo su nivel energético respectivamente.
Modo 5: Dos cúmulos de energía se forman principalmente en la zona superior de la tapa y dos lóbulos de
poca energía y menor tamaño en la zona inferior. La figura modal tiene un comportamiento en espejo con
respecto al eje vertical dejándolo con niveles de energía casi nulos, característica que comparte con el tercer
modo.
58.3 Hz
57.8 Hz
101.04 Hz
120.43 Hz
150.6 Hz
213.1 Hz
Figura 39. Modos de vibración por elementos finitos. Tapa armónica Clásica.
99.9 Hz
119.2 Hz
147.3 Hz
210.6 Hz
Figura 40. Modos de vibración por elementos finitos. Tapa armónica Flamenca.
El diseño de varillaje de las tapas Flamenca y Clásica discierne únicamente en la ubicación adicional de dos
barras en disposición de v que presenta la tapa flamenca en la zona inferior. Razón por la cual dentro de la
simulación, se observa una variación en las frecuencias propias de cada modo conservando el mismo patrón
energético en los cinco modos. En consecuencia, se expone a continuación una sola descripción del
comportamiento modal para ambos diseños.
La distribución energética del primer al cuarto modo de vibración es similar a la tapa armónica sin varillaje
descrita anteriormente. Sin embargo, la zona superior de la placa dentro del tercer modo no supera el valor
mínimo de energía, ya que los cúmulos formados no sobrepasan la boca de la guitarra. Así mismo, se
aprecia una diferencia en el cuarto modo donde tanto la región superior e inferior a la boca alcanzan niveles
máximos de energía.
El quinto modo de las tapas con varillaje, por otro lado, presenta una figura modal totalmente distinta donde
la energía permanece en la zona inferior de la superficie distribuyéndose en tres lóbulos que recogen
concentraciones máximas. Adicionalmente, sobre la boca se observa una cuarta región con una
acumulación mínima.
58.01 Hz
106.56 Hz
138.23 Hz
157.119 Hz
222.89 Hz
Figura 41. Modos de vibración por elementos finitos. Tapa armónica Folk.
Los resultados arrojados por la simulación de la tapa Folk muestran que su diseño de varillaje genera
patrones modales que difieren en el cuarto y quinto modo frente a las tapas anteriores. Aunque dentro del
cuarto modo también se forman tres regiones de concentración de energía, éstas se desarrollan con
geometrías diferentes siendo la zona central la que cubre una mayor superficie. El máximo nivel se alcanza
en la parte inferior.
La diferencia más notable se da en el quinto modo de vibración, donde se produce la mayor cantidad de
cúmulos de energía. Dentro de la superficie se distribuyen cinco zonas con un comportamiento similar dado
que ocupan aproximadamente la misma área y los niveles de energía no presentan cambios abruptos en su
escala de colores. No obstante, se adquiere el mayor nivel en un punto adyacente a la boca de la guitarra.
La siguiente tabla resume las frecuencias de resonancia que se producen en los cinco primeros modos de
vibración de cada tapa armónica. Dentro de las tapas con diseños de varillajes, la tapa Folk es aquella con
las frecuencias más altas, seguida de la Clásica mientras que los valores en la tapa Flamenca son los
menores. Entretanto, la tapa sin varillaje presenta frecuencias más bajas respecto a las demás.
Simulaciones
Frecuencias (Hz)
Modo
1
2
3
4
5
Tapa sin varillaje Tapa clásica
52.672
58.336
89.069
101.042
109.879
120.436
128.134
150.628
174.038
213.165
Tapa flamenca
57.875
99.973
119.215
147.307
210.696
Tapa folk
58.0095
106.564
138.231
157.119
222.896
Tabla 7.Frecuencias de resonancias simuladas
Nota: A pesar de conservar figuras modales similares en los tres primeros modos de vibración de cada tapa,
se evidencian cambios considerables en sus respectivas frecuencias de resonancia.
5.2 Patrones modales de Chladni
Al iniciar las mediciones para visualizar las figuras de cada modo se tuvo en cuenta los valores de frecuencia
de resonancia entregadas por la simulación, de esta manera se fue variando ascendente y
descendentemente dicho valor mientras se observaba la distribución de la sal al vibrar la superficie hasta
conseguir una figura definida y semejante a las obtenidas en la simulación.
La tapa armónica sin varillaje presentó cambios en sus frecuencias de resonancia, observándose que los
primeros cuatro modos de la medición tuvieron valores más altos con una diferencia de 4 a 13 Hz con
respecto a la simulación, mientras que el quinto modo disminuyó en 4 Hz. Dentro de los patrones modales,
el modo que mantuvo mayor concordancia con la simulación fue el primero, puesto que la sal se ubicó en las
zonas delimitadas en color azul oscuro. En contraste, el modo que mayores cambios produce es el segundo
debido a la poca cantidad de sal en la parte inferior de la tapa donde los niveles de energía fueron más
bajos. Los cúmulos de energía de las tapas restantes tienden a ser equivalentes en ambos métodos, aunque
un cúmulo de energía extra tiende a formarse en la parte superior de la placa del tercer modo donde se
evidencia la ausencia de sal.
Nota: Las figuras 42 a 45 corresponden a fotografías tomadas durante el experimento en combinación con capturas de
pantalla obtenidas en Ansys APDL.
58 Hz
93 Hz
122 Hz
135 Hz
170 Hz
Figura 42. Modos de vibración. Tapa armónica sin varillaje.
Tapa sin varillaje Frecuencia (Hz)
Modo
Simulación
1
52.672
2
89.069
3
109.879
4
128.134
5
174.038
Medición
58
93
122
135
170
Diferencia
5.328
3.931
12.121
6.866
4.038
Tabla 8. Comparación de frecuencias. Tapa sin varillaje
Las frecuencias de resonancia resultantes en el experimento de figuras de Chladni en la tapa Clásica fueron
mayores en los primeros tres modos y menores en los modos restantes en relación a los datos de la
simulación, con una diferencia en promedio de 9 Hz aproximadamente. Las distribuciones energéticas en
ambos métodos no fueron exactas, acentuándose esta característica en el tercer modo, donde la disposición
de sal sobre la boca de la tapa crea un tercer lóbulo de energía; y en el cuarto modo, en el cual los cúmulos
inferiores a la boca, a diferencia de la simulación, abarcan menor área y su proximidad forma un único foco
de energía.
La semejanza en el primer, segundo y quinto modo fue mayor en ambas técnicas, observándose que el área
delimitada en color azul oscuro corresponde a la franja donde se aglomera el material granular.
65 Hz
110 Hz
128 Hz
142 Hz
198 Hz
Figura 43. Modos de vibración. Tapa armónica Clásica
Tapa Clásica
Modo
1
2
3
4
5
Frecuencia (Hz)
Simulación
58.336
101.042
120.436
150.628
213.165
Medición
65
110
128
142
198
Diferencia
6.664
8.958
7.564
8.628
15.165
Tabla 9. Comparación de frecuencias. Tapa Clásica
La simulación y medición para la tapa Flamenca difiere en frecuencias de menor valor en promedio de 3.5
Hz aproximadamente, que resultan en el primer, segundo, tercer y quinto modo dentro del método de
elementos finitos, mientras el cuarto modo es el único con un valor más alto en 4.3 Hz.
En la visualización de los patrones modales, esta tapa tiene un alto grado de congruencia entre ambos
procedimientos donde sólo el cuarto modo presenta mayores cambios. Al igual que en la tapa clásica, las
dos regiones de concentración de energía formadas en la zona inferior de la tapa no están claramente
separadas como muestra la simulación y el tercer foco de energía en la zona superior cubre un área menor
en la medición. En los modos restantes, la ubicación de la sal en la superficie de la tapa está distribuida
como lo proyectó la simulación.
65 Hz
102 Hz
120 Hz
143 Hz
215 Hz
Figura 44. Modos de vibración por figuras Chladni. Tapa armónica Flamenca
Tapa Flamenca
Modo
1
2
3
4
5
Frecuencia (Hz)
Simulación
57.875
99.973
119.215
147.307
210.696
Medición
65
102
120
143
215
Diferencia
7.125
2.027
0.785
4.307
4.304
Tabla 10. Comparación de frecuencias. Tapa Flamenca
Con respecto a los resultados en las demás tapas, las figuras de patrones Chladni en el diseño Folk reflejan
con mayor exactitud las líneas nodales dando lugar a la formación precisa de cúmulos de energía en cada
modo, tal como se denota en el cuarto modo en el cual se hace visible la franja que separa los focos de
energía inferiores a la boca. Las características de este ejemplo aplican en los cinco modos teniendo bien
definidas las zonas que comprenden niveles bajos de energía.
Los resultados en los valores de las frecuencias de la simulación en el primer, tercer y cuarto modo son
menores, con una diferencia de 5.3 Hz en promedio, entretanto el segundo y quinto modo tuvieron
resultados mayores en 7 Hz.
61 Hz
98 Hz
140 Hz
168 Hz
217 Hz
Figura 45. Modos de vibración. Tapa armónica Folk
Tapa Folk
Modo
1
2
3
4
5
Frecuencia (Hz)
Simulación
58.0095
106.564
138.231
157.119
222.896
Medición
61
98
140
168
217
Diferencia
2.991
8.564
1.769
10.881
5.896
Tabla 11. Comparación de frecuencias. Tapa Folk
La tabla 12 reúne los valores de frecuencia de resonancia registrados durante las mediciones en cada una
de las tapas durante el método de Chladni.
Mediciones
Modo
1
2
3
4
5
Frecuencias
(Hz)
Tapa sin
varillaje
58
93
122
135
170
Tapa clásica
65
110
128
142
198
Tapa flamenca
65
102
120
143
215
Tabla 12.Frecuencias de resonancias medidas
Tapa folk
61
98
140
168
217
6. CONCLUSIONES
El primer modo de vibración se presenta formando la misma figura en las cuatro superficies, el
máximo nivel de energía se concentra en el centro de la tapa y ocupa una región ovalada de tamaño
considerable, no obstante en el diseño Folk, la figura tiene una ligera variación, donde el foco de
energía tiende a alargarse hacia la boca. Este comportamiento es consecuencia de la disposición en
X de los refuerzos principales y la ausencia de la barra transversal inferior a la boca presente en los
demás diseños.
Las figuras del segundo modo de las cuatro tapas forman dos regiones de concentración de energía.
La primera ubicada en la parte alta de la tapa con su máximo valor se conserva en los cuatro
modelos, mientras que el segundo cúmulo situado en la parte baja, aunque mantiene la misma
geometría en todos los casos, los diseños Clásico y Flamenco alcanzan un nivel energético inferior
debido a que la configuración en abanico disipa la energía.
La tapa sin varillaje produce en su tercer modo dos regiones simétricas respecto al eje vertical que
abarcan el largo de la superficie y centralizan toda la energía en la parte más ancha. Al agregar las
barras de refuerzo del mástil alrededor de la boca en las tapas Clásica y Flamenca, estos cúmulos
sólo ocupan la zona comprendida por las barras en abanico. En la guitarra Folk esta figura deja de
ser simétrica, puesto que la disposición de sus barras tampoco lo es.
En el cuarto modo de vibración de los diseños bajo estudio, se encuentran ubicadas a lo largo de la
tapa tres zonas de concentración de energía, donde los valores máximos se distribuyen en
diferentes regiones dependiendo de cada diseño. Así, los resultados de la simulación en la tapa sin
varillaje reflejan un único valor pico en la zona superior de la superficie, mientras que el diseño Folk
logra el mismo resultado en la zona inferior, puesto que aquí hay mayor libertad de vibración gracias
al reducido número de barras. A diferencia de estos diseños, la guitarra Clásica y Flamenca obtienen
dos zonas con valores máximos dejando la parte baja de la guitarra con menor energía debido a la
presencia del refuerzo en abanico.
La configuración de las barras de cada diseño estudiado experimenta las mayores diferencias
modales en el quinto modo de vibración donde no se conservan las líneas nodales entre cada tapa
armónica.
Los resultados de los diseños de las tapas Flamenca y Clásica mantienen los mismos patrones en
las figuras modales, con cambios en sus frecuencias de resonancia guardando valores cercanos.
Esto indica que las barras adicionales ubicadas en la parte inferior de la guitarra flamenca no
representan un cambio significativo en el comportamiento modal de dichos diseños.
Los resultados obtenidos en la simulación por medio de elementos finitos y la medición de patrones
sonoros de Chladni muestran un alto grado de correlación al comparar las figuras modales de las
cuatro tapas armónicas escogidas, siendo el diseño de guitarra Folk aquél que conserva mayor
similitud entre ambos procedimientos.
En el cuarto modo de vibración de las tapas Clásica y Flamenca, las imágenes arrojadas por la
simulación exponen dos cúmulos de energía claramente separados entre sí en la zona inferior de la
placa, mientras que las figuras halladas en la medición tienden a formar un mismo foco de energía.
Lo cual indica que la barra del eje central perteneciente al abanico, al vibrar dispersa a través de su
longitud, los dos cúmulos energía.
Las frecuencias fundamentales de las tapas con diseños específicos de varillaje aumentan en
relación a la tapa sin barras, debido a la modificación de la rigidez sobre la placa al adicionar dicho
refuerzo. La tapa con la menor frecuencia fue aquella sin diseño, seguida ascendentemente de la
Flamenca, Clásica y Folk.
Las frecuencias de resonancia adquiridas mediante simulación fueron menores a las resultantes del
método experimental en la mayoría de los datos, únicamente seis modos de vibración presentaron
valores mayores, entre los cuales están el quinto modo de la tapa sin varillaje, el cuarto y quinto
modo de la tapa Clásica, el cuarto modo de la tapa Flamenca y el segundo y quinto modo de la tapa
Folk. En los cuatro casos las frecuencias fundamentales fueron menores en los resultados de la
simulación.
RECOMENDACIONES
Para la implementación del método Chladni es necesario establecer las mismas condiciones de
contorno a las que se somete la superficie bajo estudio de manera que se emule las condiciones
reales de frontera. Mediante un soporte que se ajuste a esta necesidad los resultados obtenidos
estarán sometidos a un comportamiento natural.
En el caso de modificar un parlante a través de la sustitución del diafragma por un cilindro para
inyectar energía al sistema es óptimo conseguir que tenga un diámetro pequeño permitiendo la
transmisión de vibraciones de manera puntual. Así mismo, diseñar un soporte que garantice una
altura y ángulo de incidencia constante.
Para el estudio del comportamiento en frecuencias medias y altas en tapas armónicas que difieren
en su varillaje se propone realizar un estudio por medio de respuesta al impulso donde se observe el
contenido armónico de cada diseño. La obtención del espectro frecuencial permitiría llevar a cabo
una correlación con un estudio musical que abarque las notas emitidas por el instrumento.
Dentro de la simulación en el software Ansys está la posibilidad de desarrollar cada etapa a través
del código de programación, lo cual permite hacer modificaciones de manera ágil abriendo la
posibilidad de observar cambios al variar otro tipo de parámetros como propiedades del material,
tamaño del objeto, condiciones de enmallado, entre otros, sin que esto implique iniciar en cada caso
una nueva simulación.
REFERENCIAS
Bibliografía
[1] ACERO MARTÍNEZ, Laura Vanessa. BUSTOS ORTÍZ, César Darío, GUERRERO, Carolina. Stephanie,
MURCIA. SANTANA, Javier. APONTE, Juan Martín. ACOSTA, Oscar Esneider. HERMIDA, Luis Fernando.
Obtención y análisis de la respuesta al impulso (IR) del tiple Colombiano mediante el método directo e
inverso. Programa de Ingeniería de Sonido. Universidad de San Buenaventura Bogotá. Colombia. 2010
[2]
ARANGO, Jaime. ESCOBAR, León. REYES, Carlos. Figuras de Chladni en tambores. Universidad
del Valle, Cali. Colombia. 2012
[3]
BELTRÁN, Francisco. Teoría general del método de los elementos finitos. Departamento de
mecánica estructural y construcciones industriales. España. 1999
[4]
BENADE A., Fundamentals of musical acoustics. Segunda Edición. Dover Publications, INS.,
[5]
BODENSIEK CUERVO, Rainer Enrique. BORREIRO PÉREZ, Julián Mauricio. Análisis acústico de
un recinto variando su geometría, por medio del método de elementos finitos. Tesis de grado. Universidad de
San Buenaventura, Bogotá. Colombia. 2010
[6]
CARNICERO, A. Introducción al método de los elementos finitos. Escuela técnica superior de
ingeniería, Universidad Pontificia Comillas. España. 2001
[7]
CELUGÜETA LIZARZA, Juan Tomás. Método de los elementos finitos para análisis estructural.
Campus tecnológico de la Universidad de Navarra. España. 2011
[8]
CHAPMAN, Richard. Guía completa del guitarrista. Editorial Diana. México. 1998
[9]
CORREDOR JUSTINICO, Carlos. Análisis estructural de las celdas de combustión, del componente
rotativo de la cámara de combustión a volumen constante de un motor turbofan, utilizando método de
elementos finitos. Tesis de grado. Universidad de San Buenaventura, Bogotá. Colombia. 2010
[10]
COZ DÍAZ, Juan José del. SUAREZ DOMÍNGUEZ, Francisco José. Introducción al programa
ANSYS. Escuela Politécnica Superior de Gijón. España.
[11]
ELEJABARRIETA OLABARRI, Jesús. El análisis modal: su aplicación a la acústica musical. Bilbao,
EuskoIkaskuntza - Sociedad de Estudios Vascos. 1997
[12]
FÁBREGAS IBAÑEZ, Luis. La construcción de la guitarra española. Escuela Suiza de Barcelona.
España. 2012
[13]
FLETCHER N. ROSSING T., The physics of musical instruments. Segunda Edición. Springer.
[14]
FRÍAS VALERO, Eduardo. Aportaciones al estudio de las máquinas eléctricas de flujo axial mediante
la aplicación del método de los elementos finitos. Tesis doctoral. Departamento de ingeniería eléctrica,
Universidad Politécnica de Cataluña. España. 2004
[15]
2012
GONZALEZ, Esteban. Primera aproximación a la acústica de la guitarra. Buenos Aires, Argentina.
[16]
JIMÉNEZ BASCONES, J. M. Elementos de máquinas y vibraciones. Departamento de ingeniería
mecánica, energética y de materiales. Universidad Pública de Navarra. España
[17]
MARTINEZ VILLAR, Patricia. Desarrollo de una aplicación de cálculo de respuesta en frecuencia.
Universidad de La Coruña. España. 2013
[18]
PEZZOTTI, Santiago. ANTICO, Federico. Introducción a la teoría de elementos finitos, tratamiento
de la formulación de elementos unidimensionales a partir de un método directo. Universidad Nacional de la
Plata. Argentina. 2008
[19]
ORTIZ BERROCAL, Luis. Elasticidad. Tercera edición. McGRAW-Hill. España. 1998.
[20]
ROA GARZÓN, Máximo Alejandro. GARZÓN ALVARADO, Diego Alexander. Introducción al
modelamiento por elementos finitos con ANSYS. Universidad Nacional de Colombia. Colombia. 2002
[21]
RODRÍGUEZ, Adrián. Simulación mediante el método de los elementos finitos en una estructura
metálica. Universidad Carlos III de Madrid. España. 2010
[22]
RUIZ BOULLOSA, Ricardo. “Algunas notas sobre la acústica de la guitarra clásica”. Revista
Mexicana de Física 43, nº 2, 1997.
[23]
SARMIENTO MOLINA, Luis Ernesto. PEREZ JIMENEZ, Gustavo Adolfo. Análisis acústico de la gaita
colombiana. Tesis de grado. Universidad de San Buenaventura, Bogotá. Colombia. 2006
SEGURET, Christian. El mundo de las guitarras (L’univers des guitares). Studio-París. Francia. 1997
[24]
[25]
SOLÍS RODRIGUEZ, Ernesto. Método de elementos finitos. Instituto tecnológico de Ciudad de
Juárez. México. 2013
Sitios revisados en Internet
www.violeroimaginario.blogspot.com/2011/03/la-guitarra-al-milimetro.html
www.laguitarra-blog.com/2011/02/08/la-tapa-armonica-en-la-guitarra-clasica/
www.ehu.es/rperez/Fisicabio/docs/Propiedades_elasticas.pdf
www.cienciaeingenieria.com/2012/06/re-el-sonido-puede-verse-figuras-de.html
www.estebangonzalezluthier.com/
ANEXOS
Anexo A. Simulación tapa armónica sin varillaje
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo B. Simulación tapa armónica Clásica
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo C. Simulación tapa armónica Flamenca
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo D. Simulación tapa armónica Folk
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo E. Medición tapa armónica sin varillaje
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo F. Medición tapa armónica Clásica
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo G. Medición tapa armónica Flamenca
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5
Anexo H. Medición tapa armónica Folk
Modo 1
Modo 2
Modo 3
Modo 4
Modo 5