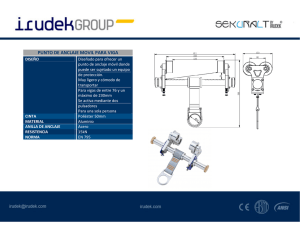
efecto de la variacion de las propiedades

UNIVERSIDAD CATOLICA DE LA SANTISIMA CONCEPCION
FACULTAD DE INGENIERIA
DEPARTAMENTO DE INGENIERIA CIVIL
EFECTO DE LA VARIACION DE LAS
PROPIEDADES GEOTECNICAS DEL
SUELO EN EL DISEÑO DE UN MURO
BERLINES
Tesis presentada a la Facultad de Ingeniería de la Universidad Católica de la Santísima
Concepción para optar al título académico de Ingeniero Civil
MARIO ANDRÉS ALARCÓN OLIVERA
PROFESOR GUIA: Dr. FELIPE VILLALOBOS JARA
CONCEPCION, ENERO 2011
UNIVERSIDAD CATOLICA DE LA SANTISIMA CONCEPCION
FACULTAD DE INGENIERIA
DEPARTAMENTO DE INGENIERIA CIVIL
EFECTO DE LA VARIACION DE LAS
PROPIEDADES GEOTECNICAS DEL
SUELO EN EL DISEÑO DE UN MURO
BERLINES
Tesis presentada a la Facultad de Ingeniería de la Universidad Católica de la Santísima
Concepción para optar al título académico de Ingeniero Civil
PROFESOR GUIA: Dr. FELIPE VILLALOBOS JARA
PROFESOR REVISOR: Dr. (CAN) MAURO POBLETE FREIRE
MINISTRO DE FE: Dr. PEDRO TUME ZAPATA
CONCEPCION, ENERO 2011
A mi Familia
Mario, Myriam y Camila
iii
Dedicatoria
El presente trabajo quiero dedicarlo a mi Familia, a mis padres Mario y Myriam, quienes
con esfuerzo me permitieron alcanzar este privilegio de poder contar con una herramienta
para mi futuro desarrollo laboral y personal. Además, les doy las gracias por inculcarme
desde pequeño que el camino del conocimiento es lo más importante para desarrollarme
como persona.
A mi hermana Camila por ser lejos la mejor.
iv
Agradecimientos
En primer lugar dar gracias a Dios por permitirme dar este paso tan importante en mi vida.
Sin él, nada de esto hubiese sucedido.
A mi profesor guía, Dr. Felipe Villalobos, por darme la posibilidad de trabajar con él y por
la disposición mostrada durante todo el período de trabajo.
A los profesores: Dr. Pedro Tume, Dr. Edwin Marcelo Behrens y al profesor Nelson
Maureira, por prestarme su ayuda y conocimientos en momentos cuando los necesité, los
admiro y respeto mucho.
A mis familiares cercanos tíos y primos, Gracias. Principalmente a mis tías Maderly y
Laura, gracias por sus palabras de aliento durante toda mi carrera universitaria.
A mis amigos de siempre, por mostrar comprensión en los momentos en que no pude estar.
A mis compañeros y amigos de universidad, aquellos quienes me acompañaron desde el
primer día como Manuel, Francisco, Alejandro, Marcos, Adrian, Carlos, María Jesús, Alex,
Benedrin, Arnaldo, Andrés y Lissette. También agradezco a quienes se unieron años más
tarde. Michael, Abraham, Claudio, Patricio, Rodolfo y Gonzalo, gracias por su amistad
desinteresada.
v
Indice de Contenidos
Dedicatoria ............................................................................................................................ iv
Agradecimientos .................................................................................................................... v
Indice de Contenidos ......................................................................................................... vi
Indice de Figuras .............................................................................................................. ix
Indice de Tablas ................................................................................................................ xi
Resumen ............................................................................................................................... xii
Summary ............................................................................................................................. xiii
1.
Introducción ................................................................................................................... 1
1.1
2.
Objetivos ................................................................................................................ 5
1.1.1
Objetivo general ................................................................................................. 5
1.1.2
Objetivos específicos ......................................................................................... 5
1.2
Justificación del problema...................................................................................... 6
1.3
Delimitación del problema ..................................................................................... 6
1.4
Metodología ........................................................................................................... 9
Marco Teórico .............................................................................................................. 11
2.1
Estructuras de contención flexibles...................................................................... 11
2.1.1
Muro berlinés ................................................................................................... 11
2.1.2
Etapas de ejecución de un muro berlinés ......................................................... 13
2.2
Teoría de empujes ................................................................................................ 14
2.2.1
Caso activo ....................................................................................................... 14
2.2.2
Caso pasivo ...................................................................................................... 16
2.3
2.3.1
Sistema de muro no anclado ................................................................................ 17
2.4
Distribución de empujes ................................................................................... 17
2.4.1
Sistema de muro anclado ..................................................................................... 17
Distribución de empujes ................................................................................... 17
2.5
Deformación de un muro de contención flexible ................................................. 20
2.6
Cargas y sobrecargas en el muro berlinés ............................................................ 21
2.7
Equilibrio de fuerzas en el muro berlinés ............................................................ 23
vi
2.7.1
Cálculo del largo de empotramiento del muro berlinés ................................... 24
2.7.2
Metodología de Blum (reducción empuje pasivo) ........................................... 25
2.8
Parámetros geotécnicos ........................................................................................ 26
2.8.1
Angulo de fricción interna del suelo ................................................................ 26
2.8.2
Cohesión........................................................................................................... 27
2.8.3
Angulo de fricción suelo-muro ........................................................................ 28
2.8.4
Peso unitario ..................................................................................................... 28
2.9
Materiales para el muro berlinés .......................................................................... 29
2.9.1
Perfiles de acero ............................................................................................... 29
2.9.2
Ademes de madera ........................................................................................... 30
2.9.3
Acero para anclajes .......................................................................................... 30
2.10
Cálculo de un muro anclado ................................................................................. 31
2.10.1
Anclaje ......................................................................................................... 31
2.10.2
Componentes de un anclaje .......................................................................... 32
2.10.3
Ubicación de la superficie potencial de falla ............................................... 35
2.10.4
Requerimientos para la separación de anclajes ............................................ 35
2.10.5
Diseño de la longitud libre ........................................................................... 37
2.10.6
Diseño de la raíz o bulbo.............................................................................. 37
2.10.7
Tracción límite
2.11
Cálculo de carga para anclajes ............................................................................. 39
2.11.1
2.12
3.
....................................................................................... 38
Empujes de suelo aparentes para muros anclados........................................ 39
Tipos de falla del suelo detrás del muro............................................................... 49
2.12.1
Falla de la cuña profunda (Cuña de Kranz) ................................................. 49
2.12.2
Seguridad a la falla por levantamiento ......................................................... 50
2.12.3
Verificación de la suma de fuerzas horizontales (Suma Horizontal) ........... 51
Modelación y Resultados ............................................................................................. 53
3.1
Caso 1: Muro berlinés sin anclaje ........................................................................ 53
3.1.1
Procedimiento de iteración ............................................................................... 55
3.1.2
Resultados ........................................................................................................ 56
vii
3.2
Caso 2: Muro berlinés con una línea de anclaje ................................................... 61
3.2.1
Procedimiento de iteración ............................................................................... 62
3.2.2
Resultados ........................................................................................................ 63
3.3
4.
Caso 3: Muro berlinés con dos líneas de anclaje ................................................. 68
3.3.1
Procedimiento de iteración ............................................................................... 69
3.3.2
Resultados ........................................................................................................ 70
Conclusiones y Recomendaciones ............................................................................... 79
4.1
Conclusiones ........................................................................................................ 79
4.2
Recomendaciones ................................................................................................. 82
4.3
Líneas futuras de investigación ............................................................................ 83
5.
Bibliografía .................................................................................................................. 85
6.
Tablas ........................................................................................................................... 88
7.
Salidas del programa .................................................................................................. 110
viii
Indice de Figuras
Figura 1 Caso de Muro Berlinés sin anclaje. ......................................................................... 7
Figura 2 Caso de Muro Berlinés con una línea de anclaje. .................................................... 7
Figura 3 Caso de Muro Berlinés con dos líneas de anclaje.................................................... 8
Figura 4 Metodología utilizada para el desarrollo de la memoria. ........................................ 9
Figura 5 Vista planta de perfiles de acero usados en un muro berlinés ............................... 12
Figura 6 Denominación para el cálculo de empuje de tierra activo (DIN 4085, 2007) ....... 15
Figura 7 Secuencia de constructiva a seguir para la colocación de anclajes (EAB 2008, R
69-1) ............................................................................................................................. 18
Figura 8 Diagramas de presiones para un muro berlinés con un soporte lateral (EAB 2008,
R 69-2) ......................................................................................................................... 19
Figura 9 Diagrama de presiones para un muro berlinés doblemente anclado (EAB 2008, R69-3) ............................................................................................................................. 19
Figura 10 Deformación en un muro flexible en diferentes etapas de construcción. ............ 20
Figura 11 Muro Berlinés sin soporte lateral: (a) excavación inicial, (b) diagrama de empujes
y fuerzas laterales, y (c) diagrama de momentos (EAB 2008 R-25.1). ....................... 21
Figura 12 Muro Berlinés con doble soporte lateral: (a) excavación final, (b) diagrama de
empujes y fuerzas laterales, y (c) diagrama de momentos (EAB 2008 R-25.2). ......... 22
Figura 13 Sobrecarga debido a situación de tráfico (EAB 2008 R-55) ............................... 22
Figura 14 Empuje adicional debido a la sobrecarga del terreno. ......................................... 23
Figura 15 Teoría de Blum .................................................................................................... 25
Figura 16 Ensayo de corte directo (DAS, 2001). ................................................................. 26
Figura 17 Ensayo de corte directo con variable Cohesión. .................................................. 27
Figura 18 Mecanismo básico de un anclaje. ........................................................................ 32
Figura 19 Componentes de un anclaje (FHWA, 1999). ....................................................... 33
Figura 20 Componentes de un anclaje con tendón de barra (FHWA, 1999). ...................... 34
Figura 21 Corte de un tendón de cables (FHWA, 1999)...................................................... 34
Figura 22 Requerimientos para la separación vertical y horizontal para anclajes (FHWA
1999). ........................................................................................................................... 36
ix
Figura 23 Envolventes de empujes aparentes de Terzaghi y Peck....................................... 41
Figura 24 Cálculo de las cargas del anclaje para un muro con un nivel de anclajes. .......... 42
Figura 25 Cálculo de cargas en anclajes para un muro con varios niveles de los mismos
(FHWA, 1999). ............................................................................................................ 43
Figura 26 Componentes de la fuerza ha la que está sometido el anclaje (FHWA, 1999). ... 44
Figura 27 Recomendación de diagrama de presión de suelo aparente para arenas (FHWA,
1999) ............................................................................................................................ 45
Figura 28 Método de equilibrio de fuerzas para muros anclados (FHWA, 1999) ............... 48
Figura 29 Superficie de falla profunda compuesta. ............................................................. 49
Figura 30 Ejemplo de superficie de falla por cuña que no se investigará. ........................... 49
Figura 31 Falla por levantamiento del fondo para un muro con sobrecarga (EAB 2008,
R10) .............................................................................................................................. 50
Figura 32 Sumatoria de fuerzas horizontales igual cero para muro berlinés (EAB 2008,
R15) .............................................................................................................................. 51
Figura 33 Muro berlinés sin anclaje. .................................................................................... 53
Figura 34 Muro berlinés con una línea de anclajes. ............................................................. 61
Figura 35 Muro berlinés con dos líneas de anclajes. ........................................................... 68
x
Indice de Tablas
Tabla 1 Proyectos de muro berlinés en la ciudad de Concepción. ......................................... 2
Tabla 2 Etapas de ejecución de un muro berlinés. ............................................................... 13
Tabla 3 Perfiles de acero HEB. ............................................................................................ 29
Tabla 4 Acero para anclajes ................................................................................................. 30
Tabla 5 Parámetros geotécnicos utilizados caso 1. .............................................................. 54
Tabla 6 Perfiles de acero usados en la modelación en GGU-RETAIN. ............................. 54
Tabla 7 Desplazamiento de la corona del muro en mm. para un δ/φ=0,5. .......................... 58
Tabla 8 Desplazamiento de la corona del muro en mm. para un δ/φ=0,667. ...................... 59
Tabla 9 Desplazamiento de la corona del muro en mm. para un δ/φ=1. ............................. 60
Tabla 10 Parámetros de la modelación caso 2. .................................................................... 62
Tabla 11 Parámetros de la modelación caso 3. .................................................................... 69
xi
Resumen
Debido a que el muro Berlinés es una técnica muy utilizada hoy en día en algunas
ciudades de Chile, como por ejemplo Concepción y Viña del Mar, se considera importante
investigar el comportamiento de dicha estructura de entibación.
El trabajo consta del estudio de tres configuraciones de muro distintas en su
geometría, usando un muro sin anclajes, otro con un anclaje y por último uno con dos
anclajes. Dichos modelos se sometieron a distintos cambios en sus parámetros geotécnicos,
tales como: el ángulo de fricción interna del suelo y la cohesión, además de cambios
geométricos como la distancia de separación entre perfiles de acero, el ángulo de
inclinación del o los anclajes y cambios de materiales como tipo de perfiles de acero y
ademes. Dichas modelaciones se realizaron en el programa de ingeniería GGU-RETAIN.
La idea de variar dichos parámetros geotécnicos es demostrar la sensibilidad que
puede llegar a poseer el diseño del muro Berlinés ante una pequeña variación de alguno de
los parámetros geotécnicos, lo que puede conllevar a realizar diseños sobredimensionados o
lo que es peor aún, subdimensionar estructuras de contención lo que puede inducir un
peligro altísimo, por cuanto esta situación pone en riesgo no sólo la integridad de la obra y
estructuras vecinas sino también la vida de la personas.
Se ha logrado concluir que el parámetro más influyente en el diseño final del muro
berlinés es el ángulo de fricción interna del suelo, el cual tiene la mayor incidencia en el
total de parámetros estudiados en esta memoria (tipo de perfil a utilizar, longitud de
enterramiento del perfil, desplazamientos horizontales máximos, longitud y carga de
anclajes y espesor de ademes de madera utilizados).
xii
Finalmente, si los parámetros geotécnicos estudiados son determinados con un alto nivel de
confianza, es decir, se cuenta con una base suficiente de datos de buena calidad obtenida de
ensayos in situ y en laboratorio, es posible reducir costos en el proyecto de entibación.
xiii
Summary
Berliner wall (soldier pile wall) is a technique widely used today in cities of Chile,
for example Concepción and Viña del Mar, for that reason it is important to investigate the
response of this type of retaining structure.
The work consists in three configurations of wall different in the geometry, using a
wall without anchors, another with one anchor and finally one with two anchors. These
models were subjected to various changes in their geotechnical parameters, such as: the
angle of internal friction of the soil and soil cohesion, as well as geometrical parameters
such as the distance of separation between profiles of steel section piles, the angle of
placement of anchors, and material parameters such as steel type section and timber
thickness. These models were made in the engineering program GGU-RETAIN.
The idea of changing these geotechnical parameters is to study the sensitivity of the
Berliner wall design due to slight variations of the geotechnical parameters, which can lead
to over dimensioned designs or worse yet, under dimensioning retaining structures which
induces a high risk, because this puts at risk not only the integrity of the site and
surrounding structures but also the lives of the people.
It has been concluded that the most influential parameter in the final design of the
Berlin wall is the soil angle of internal friction, which has the greatest impact on the overall
parameters studied in this work (type of steel profile to use, length of burial steel profile,
maximum horizontal displacements, length and load of anchors and timber thickness used).
Finally, if the geotechnical parameters are studied with a high level of confidence, i.e.
a sufficient data base of reliable quality obtained from in situ tests and laboratory tests, it is
possible to reduce costs in the retaining structure project.
Capítulo 1
Introducción
1. Introducción
El sistema de entibación muro berlinés es una técnica desarrollada por los alemanes a
comienzos de los años 1930-1940, pero no es hasta los años 90 cuando se comienza a
utilizar en la ciudad de Concepción, Chile. Dicha práctica aún no posee estudios acabados
respecto al comportamiento de dicha metodología de trabajo en nuestro país, por lo que se
decide trabajar en el tema. Es importante conocer cómo se determina la longitud de
empotramiento que debe tener el muro para que este sea suficientemente seguro, o evaluar
el comportamiento del empuje sobre el muro. Además, revisar si los parámetros
geotécnicos del suelo tienen o no incidencia en cuanto al cálculo final del muro berlinés. En
base a lo anterior, se modelaron tres distintos tipos de muros berlineses, donde el primero
será muro sin soportes laterales y las dos restantes modelaciones serán con un soporte
lateral y el tercer caso con dos. El ángulo de fricción interna del suelo φ, la cohesión c, la
separación entre perfiles de acero hincados s y el ángulo de inclinación del anclaje θ, son
algunos de los parámetros que se estudiarán.
Como se menciono anteriormente, en la ciudad de Concepción esta técnica se comenzó
a utilizar a principios de los 90, y se ha asentado con el correr de los años por su rápida
construcción y bajo costo en comparación con otros métodos de entibación, como por
ejemplo, el muro pantalla.
1
Algunas de las obras que se han realizado en la ciudad de Concepción en los últimos
años se presentan en la Tabla 1:
Tabla 1 Proyectos de muro berlinés en la ciudad de Concepción.
Nombre del Proyecto
[m²] construidos de muro
Año de construcción
-
2007
Edificio City II
1330
2007
Edificio Colo Colo
1317
2007
Hospital traumatológico
-
2007
Edificio Don Alberto
-
2008
Edificio Espacio Mayor
897
2008
Palacio de los Tribunales
3596
2009
Edificio Orompello
660
2009
Santo Tomas, sede
709
2010
1200
2010
Juzgado de Garantía
325
2010
Edificio Maipú/Aníbal
508
2010
946
2010
Edificio Murano
Concepción II etapa
Edificio de Oficinas
(Lomas de san Andrés)
Pinto
Edificio Pedro de Valdivia
También, interesa conocer lo sensible que puede llegar a ser el diseño de un muro
berlinés al ser modificado el ángulo de fricción interna o la cohesión del suelo detrás del
muro. Otro motivo por el que se lleva a cabo este estudio, es conocer la incertidumbre que
ocurre al diseñar un muro berlinés.
Para el diseño de un muro berlinés, generalmente no se cuenta con la mecánica de
suelos adecuada para su correcto dimensionamiento, lo que podría suscitarse en
2
sobredimensionamientos o lo que es peor aún, hacer un subdimensionamiento de la
estructura.
El estudio de parámetros geotécnicos nace de la investigación del ingeniero inglés
Derek Egan [8], el que presenta un estudio de 221 ensayos in situ en Inglaterra. Un tercio
de estos ensayos resultaron pobres e insuficientes a la hora de ejecutar las obras pertinentes.
De aquí se desliza una problemática que se pudiese mejorar realizando los ensayos
geotécnicos adecuados a cada proyecto en estudio. Este trabajo llama a tomar conciencia
acerca de lo anterior e invita a que se realice una mecánica de suelos adecuada para este
tipo de sistema de entibación.
Para llevar a cabo las tres modelaciones de muro berlinés, se utilizo el programa de
ingeniería GGU-RETAIN, el que por su forma rápida y sencilla de trabajar, hizo de esta
modelación una evaluación certera para cada caso estudiado.
Las modelaciones mediante GGU-RETAIN consistieron en tres casos:
1. Muro berlinés sin anclaje
2. Muro berlinés con una línea de anclaje
3. Muro berlinés con dos líneas de anclaje
Para el primer caso, se modelo un muro de 4 m. de altura y sin anclajes, las variables a
estudiar fueron cuatro: tipo de perfil a utilizar, ángulo de fricción suelo-muro δ/φ, ángulo
de fricción interna del suelo φ y la cohesión c. En el segundo caso, muro con 6 m. de altura
y una línea de anclajes distante 1,8 m. de la corona, se emplearon 3 parámetros de estudio:
ángulo de fricción interna del suelo φ, ángulo de inclinación del anclaje θ y la separación
entre perfiles de acero s a utilizar. La tercera y última modelación consistió en evaluar un
muro de 10 m. de profundidad, con dos líneas de anclaje, una a 2,5 m. de la corona del
muro y la otra ubicada a 6,25 m. de la misma .La cohesión, para ambos casos con anclaje se
considero nula.
El efecto que puede tener la napa freática en un muro berlinés sobre el nivel de
excavación no es estudiado en este caso, ya que este muro es del tipo permeable, por lo que
no tiene sentido involucrar en el diseño dicho parámetro. Además, todo lo que respecta a
vigas de amarre y extracción de las mismas, no será estudiado en esta memoria.
3
MURO BERLINES
Corona del muro
Ademes de
madera
Línea superior de
anclajes
Anclaje
Línea inferior de
anclajes
Sep
arac
ión e
Nivel final de
excavación
ntre
perf
iles
Anclaje
|
Perfil de acero
Figura 1 Composición de un muro berlinés
4
1.1 Objetivos
1.1.1 Objetivo general
Evaluar el comportamiento de un muro berlinés, anclado y no anclado, al ser sometido a
cambios en los parámetros geotécnicos del suelo (ángulo de fricción interna del suelo) y
variaciones en cuanto a parámetros de diseño del muro (separación entre perfiles y el
ángulo de inclinación del anclaje).
1.1.2 Objetivos específicos
Determinar la sensibilidad de los parámetros geotécnicos en el diseño de un muro berlinés.
Entender el comportamiento de un muro berlinés anclado y sin anclar, sometido a
variaciones en sus parámetros geotécnicos.
Conocer la relación entre la longitud de enterramiento dada la variabilidad presente del
ángulo de fricción de suelo.
Analizar el comportamiento de los anclajes debido a cambios en variaciones de parámetros
geotécnicos como estructurales.
Emplear GGU-RETAIN como herramienta para realizar análisis de sistemas de muros
simples y complejos.
5
1.2 Justificación del problema
En la actualidad Chile no cuenta con estudios de sensibilidad de muros del tipo
berlinés, por lo que resulta interesante mostrar el comportamiento del mismo al ser
sometido a distintas modelaciones y variabilidades en el ángulo de fricción interna del
suelo, ángulo de inclinación de anclajes o separación entre perfiles de acero, entre otros. Es
importante hacer ver que se debe contar con una mecánica de suelos adecuada para no caer
en dimensionamientos erróneos para sistemas de entibación.
1.3 Delimitación del problema
El problema del muro berlinés se limitó en cuanto en tres casos, los que a su vez
fueron contenidos y trabajados con diferentes condiciones de trabajo. Es así como para el
caso de muro sin anclaje se considero un peso unitario de suelo de
boyante de
, una sobrecarga de
y peso
y φ, c, δ/φ variables. También se
estudiaron tres tipos de perfiles HN. En el caso del muro con una línea de anclaje, la
sobrecarga fue de
, cohesión nula y peso unitario del suelo de
. El
ángulo de fricción del suelo φ, el ángulo de inclinación del anclaje θ y el parámetro
separación entre perfiles s se mantuvieron variables. Para el caso de dos líneas de anclajes,
las variables fueron las mismas salvo el peso unitario del suelo de
En las Figuras 2, 3 y 4 se presentan los tres casos estudiados en esta memoria.
6
Muro Berlinés sin anclaje
P`=40 KN/m²
P=10 KN/m²
Suelo
γ=19KN/m³
γs=10KN/m³
φ, C y δ/φ variables
L (m)
1.00 m
4.00 m
Perfil tipo
HN30X180,
HN40X301 ó
HN50X462
Nivel Freático
Figura 2 Caso de Muro Berlinés sin anclaje.
La sobrecarga P´(sobrecarga debido al tránsito de maquinaria pesada a un costado del
sistema de entibación) está desarrollada sobre 1,5 m detrás del muro berlinés y la
sobrecarga P sobre todo el suelo retenido.
Muro Berlinés con anclaje
1,8 m
P=10 KN/m²
6m
Ѳ
Lm
Suelo
Φ=(variable 28°-37°)
Ѳ= (variable 10°, 20° y 30°)
C= 0 kPa γ=20 KN/m³
Figura 3 Caso de Muro Berlinés con una línea de anclaje.
7
Muro Berlinés con 2 líneas de anclaje
2,5 m
P=10 KN/m²
Suelo
Φ=(variable 28°-37°)
Ѳ= (variable 10°, 20° y 30°)
C= 0 kPa
γ=18 KN/m³
3,75 m
Longitud de anclaje
óptima según el tipo de
acero
Ѳ
Lm
3,75 m
10 m
Ѳ
Perfil óptimo
Figura 4 Caso de Muro Berlinés con dos líneas de anclaje.
8
1.4 Metodología
La metodología aplicada a este estudio se esquematiza en la Figura 5 lo que se
explica con detalle en la sección Modelación.
Búsqueda de
información
Buscar
parámetros
sensibles de suelo
Utilización GGURETAIN
Incorporar
parámetros al
programa
Modelación de
muros
Modelación de
Muro sin anclajes
Modelación de
Muro con una
línea de anclajes
Modelación de
Muro con dos
líneas de anclajes
Revisión de datos
y comparación
Corroborar valores
extraídos del
programa con
planillas de
calculo
Conclusiones
Figura 5 Metodología utilizada para el desarrollo de la memoria.
9
Capítulo 2
Desarrollo
2. Marco Teórico
2.1 Estructuras de contención flexibles
La resistencia de los muros de contención está provista por la resistencia al corte y a
la flexión brindada por los elementos verticales del muro, por la resistencia pasiva del suelo
debajo del nivel de excavación y por la resistencia lateral dada por los anclajes de tierra que
resisten las presiones horizontales que actúan en el muro.
Son varios los materiales de construcción y métodos que se utilizan por los elementos
constitutivos del muro. Los elementos verticales individuales ya mencionados, a menudo
son pilotes de acero o perfiles que son dispuestos en perforaciones previas y sus paramentos
pueden ser revestimientos de hormigón moldeado in situ, entablonados de madera o paneles
premoldeados de hormigón. Los elementos continuos no requieren un revestimiento
estructural por separado y pueden ser tablestacados de acero o paneles de hormigón
moldeados in situ o premoldeados.
Los muros continuos comúnmente son utilizados para soportes temporales de
excavaciones. Los que están hechos de tablestacas se construyen hincando cada tablestaca
hasta la altura necesaria de proyecto. Por lo tanto, no son convenientes para terrenos duros
pues se dificulta el hincado.
2.1.1 Muro berlinés
El muro berlinés nace en los años 30 durante la construcción de las líneas ferroviarias
subterráneas en la ciudad de Berlín. Este tipo de muro se compone verticalmente de perfiles
metálicos hincados o colocados en perforaciones y horizontalmente de ademes en general
de madera, que se van colocando a medida que avanza la excavación. Los perfiles
11
metálicos, separados 1,5 a 3,5 metros entre sí, pueden ser perfiles laminados o compuestos.
Como perfiles laminados es frecuente el uso de perfiles del tipo H, mientras que los perfiles
compuestos se conforman generalmente de dos perfiles del tipo C unidos mediante barras o
placas metálicas (ver Figura 6). En este tipo de muro se logran apoyos intermedios directos
sobre los perfiles o indirectamente a través de cordones de arriostre. En aquellos casos en
que no sea estrictamente necesario un muro impermeable y rígido, el muro berlinés es la
solución más económica y flexible.
Figura 6 Vista planta de perfiles de acero usados en un muro berlinés (GGU-RETAIN)
Otra particularidad que presenta este sistema de entibación es la permeabilidad, lo
que impide el aumento de presiones hidráulicas perjudiciales detrás del muro berlinés. Si la
excavación se encuentra por debajo de la napa freática se debe recurrir al uso de sistemas
de agotamiento de napa, como por ejemplo punteras.
Para el caso de un sistema de muro berlinés, tanto anclado como no anclado, el
parámetro que limita el diseño es el desplazamiento horizontal del muro, debido a que no
puede existir un desplazamiento mayor a los 20 mm. [13]
12
2.1.2 Etapas de ejecución de un muro berlinés
Tabla 2 Etapas de ejecución de un muro berlinés.
Paso 1: Hincado del perfil
Paso 2: Instalación de tablones
Paso 3: Perforación y colocación de anclajes
Paso 4: Instalación y vigas de amarre
Paso 5: Tensado de anclajes
Paso 6: Término de la obra
13
2.2 Teoría de empujes
Las teorías clásicas de empuje basadas en criterios de plasticidad resultan en
distribuciones triangulares de esfuerzos horizontales de empuje. Se consideran entre estas
teorías la de Rankine y la de Coulomb. Sin embargo, a partir de estudios experimentales en
laboratorio y en terreno se ha encontrado que una distribución triangular no siempre es
apropiada. Es por ello que se han propuesto normativas y recomendaciones que incluyen
otros tipos de distribuciones, tales como rectangulares o trapezoidales, entre otras. El
programa GGU-RETAIN considera casos de distribución basados en la EAB (2008),
rectangular, birectangular, triangular, trapezoidal, cuadrilateral e incluso es posible
incorporar una distribución predefinida. Para calcular el empuje activo es posible usar la
teoría de falla de Coulomb o utilizar las recomendaciones de la norma alemana DIN 4085.
Sin embargo, esta norma presenta la distribución clásica de empujes triangular para el caso
de muro sin línea de anclajes (Figura 7). A continuación se presenta el caso activo y caso
pasivo según la DIN 4085 (2007), donde se aplica un coeficiente de empuje activo de
Müller-Breslau, en vez del coeficiente de empuje de Coulomb.
2.2.1 Caso activo
El empuje activo para un muro vertical se calcula como sigue:
(2-1)
Donde las componentes de la fuerza horizontal y vertical del empuje activo del suelo
son:
(2-2)
(2-3)
El coeficiente de empuje activo de la componente horizontal del empuje de suelos se
calcula como:
14
(2-4)
Donde la superficie de falla del suelo se desarrolla en el ángulo
es
(2-5)
En el caso especial donde α=β=δ=0,
(2-6)
(2-7)
Figura 7 Denominación para el cálculo de empuje de tierra activo (DIN 4085, 2007)
15
2.2.2 Caso pasivo
Para el caso pasivo, la componente horizontal del empuje pasivo correspondiente a la
carga del suelo retenido, en este caso, delante del muro bajo el nivel de excavación es:
(2-8)
Donde
es el coeficiente de empuje pasivo obtenido del Gráfico 1.
En el caso especial donde α=β=δ=0, el ángulo de inclinación de la superficie de falla
puede ser adoptado con el valor de
.
El coeficiente de empuje pasivo en este caso es el de Rankine:
(2-9)
Gráfico 1 Curvas del coeficiente de empuje pasivo segun el ángulo de fricción suelo-muro
(DIN 4085, 2007)
16
2.3 Sistema de muro no anclado
Consiste en una pantalla de muro que no posee soporte lateral, por ende, la capacidad
que la entibación posee por sí misma es suficiente para sostener las presiones de suelo a los
que se encuentra sometido el muro berlinés.
2.3.1 Distribución de empujes
En el caso de muro no anclado, la distribución de empuje es del tipo triangular, como
se muestra en la Figura 7.
2.4 Sistema de muro anclado
En el caso del muro anclado, éste posee soportes laterales que ayudan alcanzar
profundidades mucho mayores que los muros no anclados. La función de los soportes es la
de sostener la pantalla del muro en aquellos puntos críticos en donde la deformación del
muro se torna mayor a lo debido (20 mm. como máximo). Estos soportes pueden ser de dos
tipos.
-
Anclajes
-
Apuntalamientos
Siendo los anclajes los más usados debido a que no quita espacio físico de trabajo en la
obra en el caso de tránsito de maquinaria pesada. En el caso de los apuntalamientos, si bien
es cierto son más rápidos de instalar y más económicos, no son de mucha utilidad cuando
se cuenta con zonas de trabajo reducidas.
2.4.1 Distribución de empujes
La distribución de empujes para el caso de un muro berlinés, según la EAB 2008 [4],
presenta variados casos según la geometría y la colocación del o los soportes del problema
en cuestión.
17
2.4.1.1 Distribución de empujes de muros berlineses con uno o más soportes laterales
Para que se cumplan las siguientes distribuciones de presiones sobre el muro berlinés,
se debe satisfacer lo siguiente:
La superficie de suelo debe ser horizontal,
Se debe presentar un suelo del tipo cohesivo o no cohesivo, medianamente
denso o densamente compactado,
Debe existir un apoyo no flexible, según R 67 (EAB 2008),
Al realizar una excavación, se debe seguir la secuencia constructiva según la
Figura 8.
Nivel de soporte a ser instalado
1/3 · h
Nivel de excavación antes de instalar el soporte
h
2/3 · h
Nivel de excavación después de instalar el soporte
Figura 8 Secuencia de constructiva a seguir para la colocación de anclajes (EAB 2008, R
69-1)
A continuación se presentan los posibles tipos de diagramas a utilizar en esta
modelación.
18
hk
hk
H
H
eh
a) Apoyo a
hk ≤ 0.1 H
hk
eho
eho
H
ehu
ehu
b) Apoyo a
0.1 H ≤ hk ≤ 0.2 H
c) Apoyo a
0.2 H ≤ hk ≤ 0.3 H
Figura 9 Diagramas de presiones para un muro berlinés con un soporte lateral (EAB 2008,
R 69-2)
En la Figura 10 se presentan los modelos de distribución recomendados por la EAB
(2008).
eho
H
H
eehh
eh
ehu
a) Soportes
superiores
H
b) Soportes
centrales
c) Soportes
inferiores
Figura 10 Diagrama de presiones para un muro berlinés doblemente anclado (EAB 2008,
R-69-3)
En el caso de la modelación, se utilizaron las siguientes distribuciones de empujes:
Caso sin anclaje: Distribución Clásica Triangular (Figura 7)
Caso con una línea anclaje: Distribución Bi-rectangular (Figura 9 c)
Caso con dos líneas de anclaje: Distribución Cuadrilateral (Figura 10 b)
19
2.5 Deformación de un muro de contención flexible
En el caso particular del muro berlinés, al ser un muro flexible está condicionado por
la deformación que presenta su pantalla. Es por esto que se acepta como máximo una
deformación de 20 mm. asociada al empuje del suelo y posibles sobrecargas en el muro.
A continuación se muestra un ejemplo del comportamiento de la deformación de un
muro berlinés, en las diferentes etapas de construcción de un muro con 2 líneas de anclaje.
Anclaje superior
Anclaje inferior
Deformación Muro
a)
b)
c)
d)
Figura 11 Deformación en un muro flexible en diferentes etapas de construcción.
La Figura 11 se clasifica como sigue:
a)
b)
c)
d)
Movimiento lateral del muro con la excavación en el nivel del anclaje superior.
Movimiento lateral del muro durante la colocación del primer anclaje.
Movimiento lateral del muro con la excavación en el novel de anclaje inferior.
Movimiento lateral del muro en la condición de diseño final.
Cabe consignar que el tipo de deformación que presente el muro flexible en el
proceso de diseño, es totalmente gobernado por el tipo de distribución de empujes que se
utilice.
20
2.6 Cargas y sobrecargas en el muro berlinés
El empuje tiene un rol importantísimo en la generación de un sistema de entibación
con el muro berlinés, ya que es éste el que condiciona el tipo de desplazamiento horizontal
que ocurrirá en el muro. Generalmente, es el empuje activo el que gobierna el tipo de
diseño, ya que se encuentra presente detrás del muro de contención, y bajo el nivel de
excavación es el empuje pasivo el que se genera a lo largo de la profundidad de
enterramiento del perfil hincado. En las Figuras 12b y 13b se presenta los diagramas de
empujes y momentos flectores para un muro no anclado y muro anclado respectivamente.
H
B
t
t1
h ,k
C
H
t
t
h ,k
t1
ph,k
a)
H
b)
c)
Figura 12 Muro Berlinés sin soporte lateral: (a) excavación inicial, (b) diagrama de empujes
y fuerzas laterales, y (c) diagrama de momentos (EAB 2008 R-25.1).
21
H
B
t
h ,k
C
t1
h ,k
H
t
t
t1
ph,k
a)
H
t1
b)
c)
Figura 13 Muro Berlinés con doble soporte lateral: (a) excavación final, (b) diagrama de
empujes y fuerzas laterales, y (c) diagrama de momentos (EAB 2008 R-25.2).
Además de los empujes laterales de suelo, hay otros que se generan a partir de
sobrecargas en la corona del muro. Estas son sobrecargas que pueden ser del tipo carga
muerta o carga viva, siendo estas últimas constantes o variables. Para el caso de la
modelación
en
GGU-RETAIN,
se
adoptó
la
recomendación
incluida
en
las
recomendaciones alemanas para excavaciones, EAB 2008 [4], la que sugiere usar una carga
distribuida sobre el terreno de
para representar el efecto de calles y veredas mas
sus cargas vivas. En la Figura 14 se muestra lo anteriormente expuesto.
1,50 m
P´
P=10 KN/m²
Muro de contención
Figura 14 Sobrecarga debido a situación de tráfico (EAB 2008 R-55)
22
La distribución de empujes debido a una sobrecarga sobre el terreno detrás del muro
flexible es del tipo rectangular, como se muestra en la Figura 15.
P
H
½H
½H
Ka P
Caso Activo
Kp P
Caso Pasivo
Figura 15 Empuje adicional debido a la sobrecarga del terreno.
2.7 Equilibrio de fuerzas en el muro berlinés
En un muro berlinés, se deben considerar todas las fuerzas horizontales presentes a lo
largo del muro, como parte de un equilibrio de fuerzas horizontales dentro de la altura de la
excavación, donde las fuerzas resistentes ofrecidas en la interacción del suelo y el muro
deben superar a las fuerzas solicitantes producto de los empujes laterales.
Para la determinación de la profundidad de enterramiento de los perfiles de acero
utilizados en la construcción del muro berlinés, se determino realizando un equilibrio de
fuerzas horizontales y un equilibrio de momentos flectores. (Ver Figuras 12 y 13).
En dichas figuras se muestra una carga denominada C, la que se genera por el
equilibrio de momentos y está ubicada justo en el punto de rotación del muro. Si en el muro
se produce rotación, sucede que el empuje pasivo se traslada de izquierda a derecha, lo que
genera la fuerza C, con esto se pretende incorporar una reducción de empuje pasivo según
la metodología impuesta por Blum.
23
2.7.1 Cálculo del largo de empotramiento del muro berlinés
Para el cálculo de del largo del empotramiento del muro, existen dos métodos
propuestos en las recomendaciones alemanas [4], según el punto 5.1.6.
1. Uso del soporte libre en el suelo, de acuerdo a R-14 (Sección 5.3: Presión pasiva
de suelo para muro berlinés con soportes de suelo libres) o;
2. Como una restricción de tierra o restricción parcial de tierra según R-25 (Sección
5.4: Pie de muro restringido para muro berlinés)
El utilizado para la modelación es el método 2, previsto en las Figuras 12 y 13.
Si el muro está lo suficientemente embebido bajo el nivel de excavación, se puede
adoptar un grado de restricción en el suelo para determinar las fuerzas internas del suelo. El
grado de restricción depende del comportamiento de la deformación del muro. La
restricción de los perfiles de acero se puede basar en el acercamiento de carga después de
Blum, independiente de las verdaderas condiciones de tensión existentes en el suelo.
Este acercamiento teóricamente supone que los perfiles no estén sujetos a desviación
o torsión en el pie del muro.
Para el caso del empuje pasivo, se debe considerar, generalmente, un factor de
seguridad (F.S.), igual a 2 ó en un caso más restrictivo, por ejemplo, en una zona de
proyecto que cuente con ciertas dificultades en cuanto a sobrecargas excesivas presentes en
el entorno, se deberá tomar un valor mayor a 2.
La profundidad de enterramiento
, que se requiere teóricamente para la restricción
de un muro berlinés sin soportes laterales, que se muestra en la Figura 13, debe ser
aumentada por el muro
estructuralmente
a fin de aceptar la fuerza equivalente requerida
, si no se realizase un análisis más minucioso.
24
Es claro mencionar que la profundidad embebida del perfil de acero es aumentada en
un 20% del valor resultante del equilibrio de fuerzas horizontales y momentos flectores.
2.7.2 Metodología de Blum (reducción empuje pasivo)
El método de Blum consiste en la reducción del empuje pasivo presente en la zona
embebida frontal del muro berlinés. Es así como, luego de superponer los empujes activo y
pasivo reducido se procede a simplificar el diagrama de empujes resultantes. Una vez que
se obtiene el sistema simplificado, se impondrá un apoyo fijo teórico en el punto C sobre el
cual actuara la fuerza equivalente C de Blum (Figura 15). La obtención de dicha fuerza y la
longitud de enterramiento es mediante un simple análisis estático.
Figura 16 Teoría de Blum
La hipótesis fundamental de este método es que el momento de todas las fuerzas
respecto al centro de rotación C, punto de giro de la pantalla, es nulo.
25
2.8 Parámetros geotécnicos
2.8.1 Angulo de fricción interna del suelo
El ángulo de fricción interna del suelo puede ser determinado en el ensayo de una
pequeña pastilla de suelo en una caja de corte (Ensayo de Corte Directo), mediante el cual
se realizan varias pruebas de carga horizontal bajo carga normal constante [3]. El ángulo de
fricción puede determinarse trazando una grafica del esfuerzo cortante contra el esfuerzo
normal, como se muestra en la Figura 17. En el caso de arenas, dicho ángulo varía entre los
26° y 45°.
La forma de calcular el ángulo de fricción interna del suelo es la que se muestra a
continuación:
(2-10)
Donde
y
, con A: área de la sección transversal de la muestra.
Figura 17 Ensayo de corte directo (DAS, 2001).
26
Como se mencionó en el punto 1.3, se variará el ángulo de fricción en un intervalo
que va desde los 28° a 37° para el caso con líneas de anclaje, mientras que para el caso de
un muro sin anclar, se hará una modelación con valores de φ=10°, 20°, 30°, 40° y 45°.
2.8.2 Cohesión
La cohesión es una propiedad del suelo que es definida como la resistencia al corte
que presenta un suelo al ser sometido a una presión normal igual cero, que se ve graficada
Esfuerzo Cortante, s
en la zona de falla o ruptura [11] .(Ver Figura 18).
σ
=c+
tan φ
s
φ
c
Esfuerzo Normal, σ
Figura 18 Ensayo de corte directo con variable Cohesión.
Este parámetro intrínseco de cada suelo, se puede definir gracias al ensayo de corte
directo o bajo el ensayo triaxial.
Para el caso 1, la cohesión del muro sin anclar se dispuso de una variabilidad de
c = 0, 10, 25, 50,100 y 300 kPa, mientras que en el caso de muros anclados, la cohesión fue
asumida nula.
27
2.8.3 Angulo de fricción suelo-muro
El ángulo de fricción suelo-muro, denominado como δ, es aquel que se define para
saber que cantidad del ángulo de fricción interna del suelo está en contacto con la pared del
muro en estudio. En el caso 1 de muro sin anclajes, se obvió este parámetro, ya que la
cohesión al variar en algún momento puede llegar a cero, mientras que en la modelación 2
y 3, muros anclados, el ángulo de fricción suelo-muro fue adoptado como 2/3 del ángulo de
fricción interna del suelo φ.
2.8.4 Peso unitario
El peso unitario del suelo, es definido como el peso total del suelo dividido por su
volumen. En esta oportunidad, para las tres modelaciones habrá distintos valores del peso
unitario.
28
2.9 Materiales para el muro berlinés
2.9.1 Perfiles de acero
Los perfiles de acero que trae GGU-RETAIN por defecto, son perfiles del tipo HEB
europeos, con los cuales se llevo a cabo el análisis de dos de los tres casos estudiados. A
continuación se muestra las características de dichos perfiles en las Tabla 3.
Tabla 3 Perfiles de acero HEB.
Nombre
h (cm)
b (cm)
A (cm²)
I (cm⁴)
S/s (cm²)
14
14
43
1510
175,7
HEB 140
16
16
54,3
2490
221,3
HEB 160
18
18
65,3
3830
283,5
HEB 180
20
20
78,1
5700
356,7
HEB 200
22
22
91
8090
435,8
HEB 220
24
24
106
11260
527
HEB 240
26
26
118
14920
641
HEB 260
28
28
131
19270
730,5
HEB 280
30
30
149
25170
849,1
HEB 300
34
30
171
36660
1003,3
HEB 340
40
30
198
57680
1197
HEB 400
45
30
218
79890
1422,1
HEB 450
50
30
239
107200
1660
HEB 500
60
30
270
171000
2072,9
HEB 600
70
30
306
256900
2449,4
HEB 700
100
30
400
644700
3909,5
HEB 1000
Donde h es la altura del perfil, b el ancho del perfil, A el área del perfil e I la inercia.
El parámetro
corresponde a la rigidez cortante del perfil, donde S es el momento
estático medio de la sección respecto a X y s es el espesor del alma del perfil.
En cuanto a las propiedades del acero del perfil, están son:
29
2.9.2 Ademes de madera
En el caso de los ademes de madera utilizados como revestimiento del muro berlinés,
se asume una tensión admisible en flexión es de:
2.9.3 Acero para anclajes
El acero utilizado para la modelación de anclajes fue el acero tipo Litzen (liso), el que
usa el programa GGU RETAIN por defecto. Durchmesser es el diámetro del cable
flexible en mm.
A continuación se presentan una Tabla con las propiedades de cada acero.
Tabla 4 Acero para anclajes
Nombre
Carga Adm. (KN)
251
St 1570/1770 2 Litzen 0,6"
377
St 1570/1770 3 Litzen 0,6"
502
St 1570/1770 4 Litzen 0,6"
628
St 1570/1770 5 Litzen 0,6"
754
St 1570/1770 6 Litzen 0,6"
897
St 1570/1770 7 Litzen 0,6"
263
St 835/1030 Durchmesser 26,5
384
St 835/1030 Durchmesser 32
485
St 835/1030 Durchmesser 36
340
St 1080/1230 Durchmesser 26,5
496
St 1080/1230 Durchmesser 32
628
St 1080/1230 Durchmesser 36
Más adelante, en la sección de modelación, se mostraran los resultados obtenidos
mediante el programa GGU-RETAIN, el que entrega la carga a las que están sometidos los
anclajes y su respectivo tipo de acero óptimo.
30
2.10 Cálculo de un muro anclado
Como se menciono anteriormente, la modelación que se realizo consta de 3
posibilidades, siendo la segunda y la tercera del tipo muro anclado. En esta oportunidad se
debe incorporar un elemento llamado anclaje, el que es de principal importancia en este
trabajo.
A continuación se presenta el elemento anclaje.
2.10.1 Anclaje
Conceptualmente, un anclaje es un elemento estructural instalado en suelo o roca y
que se utiliza para transmitir al terreno una carga de tracción aplicada.
Las presiones que desarrollan los suelos detrás de un talud pueden absorberse
interponiendo estructuras de retención. Estas estructuras pueden estar constituidas por
muros rígidos o por sistemas flexibles. Los sistemas flexibles, como las tablestacas, los
muros pantalla, o los tabiques necesitan para su estabilidad, estar ligados a puntos fijos.
En excavaciones grandes o en taludes naturales las retenciones flexibles logran su
estabilidad generalmente con anclajes en suelo.
Por lo tanto el mecanismo básico de un anclaje consiste en transferir las fuerzas de
tracción hacia el suelo o la roca a través de la resistencia movilizada en la interfase entre el
anclaje y el material que lo rodea (raíz o bulbo).
En la Figura 19 se observa cómo funciona el mecanismo básico de un anclaje en
suelo.
31
Figura 19 Mecanismo básico de un anclaje.
2.10.2 Componentes de un anclaje
Un anclaje contiene los siguientes elementos en su composición:
-
Cabeza de anclaje
-
Tendón (Longitud libre)
-
Raíz o bulbo (Longitud de adherencia)
32
-
Figura 20 Componentes de un anclaje (FHWA, 1999).
La cabeza de anclaje es un sistema integrado por una placa de apoyo y una tuerca,
que es capaz de transmitir la fuerza desde el acero (cable) a la superficie del terreno o a la
estructura del soporte (ver Figura 21).
33
Figura 21 Componentes de un anclaje con tendón de barra (FHWA, 1999).
El tendón conecta la cabeza del anclaje con la raíz o bulbo. Este puede elongarse
elásticamente y transmitir la fuerza de resistencia de la raíz a la estructura. Para que el
acero se deforme libremente se coloca un manguito o vaina (Ver Figura 22) de material
plástico liso alrededor del tendón para impedir la adherencia del tendón con la inyección
circundante. El tendón puede estar formado tanto por cables como por barras de acero.
Figura 22 Corte de un tendón de cables (FHWA, 1999).
Por último, la raíz es un cuerpo enterrado que actúa en el extremo del anclaje, y es el
destinado a fijar la masa de suelo que lo rodea. Este cuerpo puede formarse en suelo
generalmente con una inyección controlada que adopta la forma de un bulbo ramificado.
34
Algo importante que se debe tener en cuenta, es que la raíz del anclaje debe ir por detrás de
la superficie de falla, caso que se verá a continuación.
2.10.3 Ubicación de la superficie potencial de falla
La ubicación de la superficie potencial de falla debe evaluarse a partir del concepto
que la raíz del anclaje, debe estar lo suficientemente detrás de dicha superficie para que la
carga no se transfiera desde la raíz del anclaje a la zona sin adherencia (tendón). Esta última
se define como la que está entre la superficie crítica posible de falla y el muro. La longitud
libre se extiende, usualmente, a una distancia mínima de H/5, donde H es la altura del
muro, ó, a 1,5 m. detrás de la superficie crítica de falla.
Para muros construidos en suelo no cohesivos, se puede asumir que la superficie
crítica posible de falla se extiende hacia la superficie del terreno desde el vértice de la
excavación con un ángulo de
con respecto a la horizontal (cuña activa).
2.10.4 Requerimientos para la separación de anclajes
Cada anclaje, en un sistema de anclajes, es diseñado suponiendo que el mismo
soporta un área de influencia de carga basada en la separación horizontal y vertical entre
anclajes adyacentes (área tributaria).
La separación horizontal y vertical variará de acuerdo a requerimientos de proyecto
los cuales pueden ser:
-
Necesidad de un sistema rígido (es decir anclajes poco separados) para el
control de los movimientos laterales;
-
La existencia de estructuras subterráneas que pueden afectar el
posicionamiento y la inclinación del anclaje;
-
Tipos de elementos de muro vertical seleccionados para el diseño.
35
Para anclajes instalados en suelo, se necesita una altura de 4,5 m. de la superficie del
terreno al centro de la zona de adherencia (Figura 23 a). Esto es para prevenir la pérdida de
lechada cementicia durante la instalación de los anclajes inyectados a presión y para
prevenir el levantamiento de la superficie del terreno debido a grandes presiones de
inyección. Para anclajes inyectados a gravedad, se necesita aplicar el criterio de la mínima
sobrecarga para proveer al suelo de la sobrecarga necesaria para el desarrollo de la
resistencia del anclaje.
La separación horizontal típica para las estructuras de contención de perfiles
metálicos es 1,5 m. a 3 m. para los perfiles hincados y más de 3 m. para los instalados en
perforaciones. La separación mínima entre anclajes que se muestra en la Figura 22 b,
asegura que el efecto del conjunto entre anclajes adyacentes se minimiza y se evitan las
interferencias debidas a desviaciones en las perforaciones. El efecto del conjunto reduce la
capacidad de soporte de los anclajes individuales [9].
Figura 23 Requerimientos para la separación vertical y horizontal para anclajes (FHWA
1999).
36
2.10.5 Diseño de la longitud libre
La longitud libre mínima para rocas y suelos es 4,5 m. para tendones de cables y 3 m.
para tendones de barra de acero.
Existen casos en los cuales se pueden necesitar longitudes libres mayores que las
anteriores, como por ejemplo:
-
ubicar la longitud de la raíz a una distancia mínima detrás de la superficie
potencial de falla;
-
ubicar la zona de adherencia del anclaje en un suelo apropiado para el mismo;
-
asegurar una estabilidad completa del sistema de anclajes;
-
dar lugar a movimientos a largo plazo. En general, la longitud libre se
extiende a una distancia mínima de H/5 o 1,5 m. detrás de la superficie
posible de falla para proveer una transferencia mínima de tensiones generadas
por la raíz.
2.10.6 Diseño de la raíz o bulbo
Para un proyecto en particular, el primer paso en la estimación de la capacidad
mínima del anclaje es suponer la máxima longitud de adherencia posible. En el caso de un
terreno sin restricciones se puede diseñar un anclaje con una inclinación de 15° y una
longitud de adherencia de 12 m. en suelo y de 7,5 m. en roca [9].
37
2.10.7 Tracción límite
La tracción límite del anclaje puede ser definida como:
(2-11)
Donde
: Diámetro de la raíz del anclaje.
Longitud de la raíz.
: Fricción lateral unitaria limite que se ejerce a lo largo de la superficie lateral de la
raíz o bulbo.
Una de las maneras más usadas para conocer el parámetro
es mediante el análisis
de los valores obtenidos del ensayo SPT (Standard Penetration Test).
El valor de
se debe calcular de la siguiente manera:
(2-12)
Donde
es el diámetro de perforación y
es el coeficiente de inyección, el que
depende si se utiliza el sistema IGU (Inyección Global Única) o el IRS (Inyección
Repetitiva Selectiva).
Tensión admisible
La forma de calcular la tensión admisible
, es como sigue:
(2-13)
Donde n es el número de cables,
es el área de cada cable,
es la tensión de
fluencia del cable y FS es un factor de seguridad igual a 1,5.
38
2.11 Cálculo de carga para anclajes
2.11.1 Empujes de suelo aparentes para muros anclados
2.11.1.1 Evaluación de las presiones del terreno para el diseño del muro
La distribución de empujes de suelo que se desarrollan en un muro anclado, dependen
de la magnitud y distribución de las deformaciones laterales del muro. En algunos muros
flexibles (por ejemplo, muro berlinés no anclados) puede esperarse que sufran
deformaciones laterales lo suficientemente grandes para inducir empujes activos en el
terreno en toda la altura del muro. Para el diseño de estos sistemas, pueden recurrirse a
diagramas que utilizan los métodos de análisis de Rankine o Coulomb.
Para sistemas de muros anclados, el modelo de deformación es más complicado y no
se condice con el desarrollo de la distribución de empujes teóricos de Rankine o Coulomb.
La resistencia al corte del suelo, la rigidez del muro, la inclinación del anclaje, la
separación vertical del anclaje y las sobrecargas influencian directamente en el modo de
deformación del muro y en el empuje total sobre el mismo. Los métodos para evaluar los
empujes de estos tipos de muros anclados con elementos flexibles incluyen el uso de
empujes aparentes, cuñas deslizantes y cálculos basados en equilibrio límite. Los cálculos
de equilibrio límite pueden usarse para evaluar la carga total necesaria para estabilizar un
talud o excavación en suelos altamente estratificados, perfiles de suelo para los cuales la
superficie de falla posible es profunda u ocurre a lo largo de planos definidos débiles y
donde están presentes sobrecargas complicadas. Estos tipos de cálculos pueden
desarrollarse usando métodos de cálculo manuales tales como cuñas de prueba o utilizando
programas de computación para la estabilidad de taludes (GGU-STABILITY).
Aunque los cálculos por equilibrio límite son tan válidos como por los diagramas de
empujes aparentes, se recomiendan los últimos, por su sencillez y rapidez de uso.
39
2.11.1.2 Diagramas de empujes aparentes de Terzaghi y Peck
Los diagramas de empujes aparentes, son diagramas semi-empíricos que fueron
desarrollados originalmente por Terzaghi y Peck (1967) y por Peck (1969) para el cálculo
de cargas envolventes de los puntales en excavaciones entibadas.
Los diagramas representan:
1- cargas drenadas en arena;
2- cargas no drenadas en arcillas fisuradas de firmes a duras;
3- cargas no drenadas en arcillas blandas a medias.
El análisis de los diagramas de empujes aparentes, permiten un cálculo manual
relativamente simple de cargas en el anclaje y de los momentos flexores del muro. Ellos
representan una envolvente que puede usarse para desarrollar un sistema de anclajes
adecuado para toda la vida de la excavación.
Los diagramas de Terzaghi y Peck, que son de forma rectangular o trapezoidal, se
pueden ver en la Figura 24, donde la máxima presión se denomina “p” y están basados en
las siguientes premisas:
-
Los diagramas de presiones fueron desarrollados para cortes verticales y
coronamiento horizontal, a partir de puntales instalados horizontalmente.
-
Se considera que la excavación tiene una profundidad mayor a 6 m. y que es
relativamente ancha. Se supone, además, que los movimientos del muro son
lo suficientemente grandes como para desarrollar la resistencia completa al
corte.
-
Se supone que, para arenas, el nivel freático está por debajo de la base de la
excavación, y para arcillas su posición no es de importancia. La carga debida
a la presión de agua no fue considerada específicamente en estos análisis.
40
-
Se asume que la masa de suelo es homogénea y que el comportamiento del
suelo durante el corte es en condición drenada para arenas y no drenada para
arcillas, es decir se consideran solamente las cargas a corto plazo.
-
Los diagramas de carga se aplican solo a la porción del muro expuesta y no a
aquella que está embebida en el terreno debajo del fondo de la excavación.
Figura 24 Envolventes de empujes aparentes de Terzaghi y Peck.
2.11.1.3 Cálculo de las cargas en el anclaje a partir de los diagramas de empujes
aparentes
Las cargas de los anclajes para su uso en muros flexibles anclados pueden estimarse a
partir de los diagramas de empujes aparentes, utilizando procedimientos que se usan
comúnmente incluyendo el método del área de influencia y el método de la articulación, los
que han sido desarrollados para hacer cálculos manuales en sistemas estáticamente
indeterminados (Ver Figura 25). Ambos métodos, cuando utilizan los diagramas de empuje
apropiados, han dado estimaciones bastante razonables de las cargas en los anclajes y de los
momentos flectores en el muro, cuando éste está construido en suelo competente.
41
Figura 25 Cálculo de las cargas del anclaje para un muro con un nivel de anclajes.
Los cálculos de las cargas horizontales de los anclajes según el método mencionado,
se presentan en la Figura 25 para un nivel de anclajes y en, la Figura 26, para un muro con
más de una línea de anclajes. Ambos procedimientos, suponen que se desarrolla una
articulación (en la cual el momento flector es nulo) en la base de la excavación y que dicha
base actúa como un puntal de soporte. Esta última suposición es razonable para muros que
penetran dentro de materiales competentes. El momento máximo que gobierna el diseño del
muro ocurre típicamente en la porción expuesta del mismo, es decir, sobre la base de la
excavación.
En muros construidos en materiales competentes, se supone que la fuerza de reacción
R, está soportada por la resistencia pasiva del suelo debajo de la base de la excavación. Por
ende, el muro debe estar lo suficientemente embebido para que la misma se desarrolle. En
este caso, el anclaje inferior toma solo el área tributaria del diagrama de empujes aparentes,
desde la base de la excavación hasta la mitad de la altura entre la base y su propia
ubicación.
42
Para muros que penetran en materiales débiles no habrá suficiente capacidad de
desarrollo de la resistencia pasiva disponible debajo de la excavación para soportar la
reacción, independientemente de la profundidad de penetración del muro. Para este caso el
anclaje inferior debe diseñarse para soportar carga de su área tributaria, arriba mencionada,
más la carga de la reacción.
Figura 26 Cálculo de cargas en anclajes para un muro con varios niveles de los mismos
(FHWA, 1999).
Los valores calculados usando las Figuras 26 y 27, para las cargas en los anclajes, son
la componente horizontal de la carga del anclaje por unidad de ancho del muro,
. Como
los mismos no se instalan en forma horizontal sino inclinados aparece, también, una
43
componente en dirección vertical y en sentido hacia abajo que tiene que ser solventada por
la fricción y/o adherencia entre la estructura y el suelo, denominada
(Figura 27).
Figura 27 Componentes de la fuerza ha la que está sometido el anclaje (FHWA, 1999).
La carga total del anclaje,
, se calcula como:
(2-14)
Donde s es la separación horizontal entre anclajes adyacentes.
La carga del anclaje T que se utiliza como carga de diseño se calcula como:
(2-15)
Donde θ es el ángulo de inclinación del anclaje bajo la horizontal. La componente
vertical de la carga total, T, es:
(2-16)
2.11.1.4 Recomendaciones para diagramas de presión aparente de arenas
Para arenas, el valor del coeficiente de empuje activo
es:
(2-17)
44
Y la ordenada de presión máxima de suelo es:
(2-18)
Donde φ´ es el ángulo de fricción interna de la arena. Usando este valor de presión de
suelo lateral, la carga total del diagrama de presión aparente rectangular (Figura 28 a), para
arenas es de
. La envolvente de presión de suelo aparente recomendada para uno,
dos o más niveles de anclajes sobre un muro, es de forma trapezoidal como se muestra en la
Figura 28 b.
Figura 28 Recomendación de diagrama de presión de suelo aparente para arenas (FHWA,
1999)
45
A diferencia de las envolventes de Terzaghi y Peck (1967), para los diagramas
recomendados acá, se requiere conocer la posición de los anclajes superiores e inferiores a
fin de construir el diagrama de presión de suelo aparente. El diagrama trapezoidal es el más
apropiado que el diagrama rectangular por los siguientes motivos:
-
Las presiones del suelo son concentradas en las posiciones de los anclajes,
resultantes por el efecto de arco;
-
La presión del suelo nula en la superficie del terreno es recomendada para las
arenas (a menos que exista una sobrecarga presente en el modelo);
-
Las presiones de suelo aumentan desde la superficie del terreno a la
localización del anclaje de suelo superior; y
-
De arenas densas a muy densas, las presiones de suelo se reducen bajo la
ubicación del anclaje inferior debido a la resistencia pasiva que se desarrolla
debajo de la base de la excavación.
Este diagrama es apropiado tanto para cargas a largo plazo (permanentes) como para
cargas a corto plazo (temporales) en arenas. Las cargas debido a la napa como sobrecargas,
deberán ser añadidas explícitamente al diagrama para evaluar la carga lateral total que actúa
sobre el muro.
2.11.1.5 Método de análisis de la cuña de deslizamiento
El método de equilibrio de la cuña de deslizamiento puede ser usado para evaluar la
carga horizontal requerida para proporcionar estabilidad al corte vertical. Por ejemplo una
superficie de falla, diagrama de cuerpo libre, y el diagrama del vector fuerza se muestran en
la Figura 28 para un muro de altura H con un suelo detrás y delante del muro caracterizado
por un ángulo de fricción efectivo φ. Se supone que la superficie de falla potencial crítica
pasa por delante de la raíz del anclaje, de forma que la totalidad de la carga del anclaje
contribuye a la estabilidad del muro. La resistencia al corte se factoriza por un factor de
seguridad de tal manera que:
46
(2-19)
En la porción enterrada del muro, profundidad d, se asume que se desarrolla una
resistencia pasiva. Para la superficie de falla supuesta se puede usar un ángulo de fricción δ
de la superficie igual a
En el análisis,
, para calcular el coeficiente de empuje pasivo.
representa la fuerza horizontal necesaria para dar estabilidad al
corte vertical. Esta fuerza representa la resistencia combinada por la componente horizontal
de la fuerza del anclaje,
muro,
, y la resistencia lateral dada por la porción enterrada del
.
La suposición que
perfil de acero,
carga en el anclaje,
es horizontal implica que la resistencia vertical dada por el
, es igual en magnitud y opuesta en signo a la componente vertical de la
. La fuerza resistente necesaria,
, se calcula, entonces,
como:
(2-20)
47
Figura 29 Método de equilibrio de fuerzas para muros anclados (FHWA, 1999)
La solución a la ecuación de
se encuentra iterando por medio del ángulo de la
superficie potencial de falla y de la profundidad d, hasta que se halle el máximo valor de
. Luego, esta fuerza debe distribuirse en una envolvente de empujes aparentes para el
cálculo de las cargas en los anclajes y de los momentos flectores en la porción expuesta del
muro.
48
2.12 Tipos de falla del suelo detrás del muro
2.12.1 Falla de la cuña profunda (Cuña de Kranz)
De acuerdo con la EAB (2008), R 44 [4], se debe verificar la seguridad frente a la
falla de la cuña profunda en muros anclados. Esta verificación tiene como primera medida
fijar el largo necesario de los anclajes. Para este fin, el programa GGU-RETAIN utiliza el
método descrito por Ranke y Ostermayer (1968). El programa primero investiga la
superficie de falla para cada anclaje incluyendo la influencia de los anclajes restantes en la
superficie analizada. Acto seguido, serán analizadas superficies de falla determinadas
uniendo extremos de un grupo de anclajes, incluyendo nuevamente la contribución de los
anclajes restantes en la superficie de falla analizada (ver Figura 30 y 31).
Figura 30 Superficie de falla profunda compuesta.
Figura 31 Ejemplo de superficie de falla por cuña que no se investigará.
49
La superficie de falla más desfavorable asociada con cada anclaje es determinado por
el programa con el correspondiente coeficiente de seguridad. El factor de seguridad de
utilizado en la modelación es de 1.5, el cual es requerido al usar factores globales de
seguridad. Si este factor no se alcanzara o fuera garantizado excesivamente, el programa
podrá optimizar el largo de cada anclaje individualmente, si así lo deseara el usuario.
2.12.2 Seguridad a la falla por levantamiento
La seguridad a la falla por levantamiento del fondo de la excavación (EAB 2008, R
10) se verifica mediante un análisis de capacidad de carga según Weißenbach (1977), el
cual compara fuerzas gravitacionales (incluyendo cargas distribuidas, bermas, etc.) con la
capacidad de carga. En este análisis, GGU RETAIN analiza 50 posibles planos verticales
de falla. El primer plano de falla se encuentra distanciado del muro a 0.2 veces la
profundidad de la excavación y la última a 5 veces la profundidad de la excavación. Para el
muro berlinés, el extremo inferior del plano de falla es el fondo de la excavación.
Figura 32 Falla por levantamiento del fondo para un muro con sobrecarga (EAB 2008,
R10)
50
2.12.3 Verificación de la suma de fuerzas horizontales (Suma Horizontal)
Al analizar la estabilidad de un muro berlinés (Figura 33), muestra que el empuje
activo de suelos debajo del fondo de la excavación puede ser despreciado (Ver EAB 2008,
R15). Sin embargo, debe ser demostrado que este empuje activo despreciado puede ser
tomado por el empuje pasivo de suelos con un margen de seguridad adecuado
(generalmente 1.5). Al realizar GGU-RETAIN esta verificación, puede ser que GGURETAIN automáticamente incrementa el largo embebido del muro para cumplir con las
exigencias de la EAB, R 15. Si no pudiera verificarse la estabilidad del muro, el programa
da recomendaciones de acuerdo a la EAB para lograrlo.
Figura 33 Sumatoria de fuerzas horizontales igual cero para muro berlinés (EAB 2008,
R15)
51
Capítulo 3
Modelación y Resultados
52
3. Modelación y Resultados
3.1 Caso 1: Muro berlinés sin anclaje
En este primer caso se muestra una altura de excavación de 4 m., una sobrecarga de
al costado de la excavación y una de
infinitamente desarrollada.
Esta condición es bastante desfavorable para un muro berlinés de 4 m., pero eso se
comprobará en el capítulo de resultados. Para el suelo se cuenta con un peso especifico de
y el peso boyante es de
.
Muro Berlinés sin anclaje
P`=40 KN/m²
Perfil tipo
HN30X180,
HN40X301 ó
HN50X462
Suelo
γ=19KN/m³
γs=10KN/m³
φ, C y δ/φ variables
1.00 m
Le (m)
4.00 m
P=10 KN/m²
Nivel Freático
Figura 34 Muro berlinés sin anclaje.
Las variables que se harán variar serán cuatro, y se presentan a continuación:
1. Cohesión,
2. Tipo de perfil de acero,
53
3. Angulo de fricción suelo-muro y
4. Angulo de fricción interna del suelo.
En la siguiente Tabla se muestran los valores que se adoptaron los parámetros
variables en la modelación:
Tabla 5 Parámetros geotécnicos utilizados caso 1.
Parámetros variables
φ (°)
10
20
30
40
45
C (kPa)
0
10
25
50
100
δ/φ
0,5
0,667
300
1
Solo en este caso se dejaron fijos los perfiles de acero a utilizar, ya que en el caso de
muros anclados se busco el perfil óptimo según la ocasión. Estos perfiles HN fueron
extraídos del manual CINTAC.
Tabla 6 Perfiles de acero usados en la modelación en GGU-RETAIN.
Perfil
Área (cm²)
W (cm³)
I (cm⁴)
E (KN/cm²)
HN 30X180
230
2430
36400
2,1x10⁴
HN 40X310
384
54800
110000
2,1x10⁴
HN 50X462
588
10600
266000
2,1x10⁴
54
3.1.1 Procedimiento de iteración
Los siguientes son los pasos que se adoptaron para llegar a los resultados del
programa:
1. Se modela la geometría del problema con sus respectivas dimensiones en el
programa de ingeniería GGU-RETAIN. Esto se realiza solo una vez.
2. Se ingresan los datos geotécnicos para la primera iteración del muro.
3. La distancia entre perfiles, para este caso, fue de 1,6 m. [13]
4.
Luego se adopta la forma en que determina el empuje activo y pasivo del
modelo. [5]
5. Se ingresan las cargas distribuidas al programa.
6. Se fija el tipo de perfil a utilizar.
7. Se calcula el sistema y se procede a guardar la información obtenida para su
análisis.
55
3.1.2 Resultados
A continuación se presentan una serie de gráficos con los resultados obtenidos a
través de la modelación en GGU-RETAIN para un muro berlinés sin anclajes.
Gráfico 2 Longitud de enterramiento del perfil.
En el Gráfico 2 se ve claramente la influencia tanto del ángulo de fricción interna del
suelo como de la cohesión en el comportamiento de la longitud de enterramiento del perfil
de acero del muro berlinés sin anclaje. Además, el ángulo de fricción suelo-muro tiene una
pequeña influencia en la longitud de enterramiento, pero no alcanza a ser importante en
comparación a los parámetros antes mencionados.
De esta manera, se puede decir que a mayor φ (°) menor longitud de enterramiento.
Así también, a mayor c (kPa) menor longitud de enterramiento.
En las Tablas 7, 8 y 9, se presentan los desplazamientos horizontales máximos que
ocurren en la corona del muro berlinés, debido a la variación de los parámetros geotécnicos
de la modelación.
56
De estas secuencias graficas se concluye que el comportamiento del desplazamiento
con respecto al ángulo de de fricción interna del suelo, ángulo de fricción suelo-muro, perfil
de acero utilizado y la cohesión es como sigue:
-
A mayor φ, menor desplazamiento del muro.
-
A mayor δ/φ, menor desplazamiento del muro.
-
A mayor Perfil de acero, menor desplazamiento
-
A mayor c, menor desplazamiento del muro.
A continuación se presentan las secuencias de graficas con el comportamiento del
desplazamiento horizontal máximo.
Cabe destacar que el desplazamiento horizontal máximo para diseño no debe superar
los 20 mm., en caso contrario se necesitara utilizar anclajes para disminuir dicha
condición de borde.
En el Anexo 3 se muestra en detalle lo anteriormente mencionado.
57
Tabla 7 Desplazamiento de la corona del muro en mm. para un δ/φ=0,5.
En esta secuencia se presenta un análisis de
sensibilidad al ángulo de fricción interna del
suelo, con una valor constante del ángulo de
fricción suelo-muro de δ/φ=0,5. Se muestra
que tanto la cohesión, el ángulo de fricción
interna del suelo y el tipo de perfil utilizado son
factores determinantes a la hora de verificar el
desplazamiento máximo.
58
Tabla 8 Desplazamiento de la corona del muro en mm. para un δ/φ=0,667.
En esta secuencia se presenta un análisis de
sensibilidad al ángulo de fricción interna del
suelo, con una valor constante del ángulo de
fricción suelo-muro de δ/φ=0,667. Se muestra
que tanto la cohesión, el ángulo de fricción
interna del suelo y el tipo de perfil utilizado son
factores determinantes a la hora de verificar el
desplazamiento máximo.
59
Tabla 9 Desplazamiento de la corona del muro en mm. para un δ/φ=1.
En esta secuencia se presenta un análisis de
sensibilidad al ángulo de fricción interna del
suelo, con una valor constante del ángulo de
fricción suelo-muro de δ/φ=1. Se muestra que
tanto la cohesión, el ángulo de fricción interna
del suelo y el tipo de perfil utilizado son
factores determinantes a la hora de verificar el
desplazamiento máximo.
60
3.2 Caso 2: Muro berlinés con una línea de anclaje
Para el caso de muro berlinés con una línea de anclajes se uso una altura de
excavación de 6 m., una línea de anclajes a 1,8 m. de la corona del muro y una sobrecarga
de
infinitamente desarrollada. Para el suelo se cuenta con un peso especifico de
y el peso boyante es de
. La napa se encuentra al nivel de la
excavación.
Muro Berlinés con anclaje
1,8 m
P=10 KN/m²
6m
Ѳ
Lm
Suelo
Φ=(variable 28°-37°)
Ѳ= (variable 10°, 20° y 30°)
C= 0 Kpa γ=20 KN/m³
Figura 35 Muro berlinés con una línea de anclajes.
Las variables que se harán variar serán cuatro, y se presentan a continuación:
1. Angulo de fricción interna del suelo,
2. Angulo de inclinación del anclaje y
3. Separación entre perfiles de acero.
La cohesión en esta oportunidad se mantuvo constante, con una valor de 0 kPa.
En la siguiente Tabla se muestran los valores que se adoptaron los parámetros
variables en la modelación:
61
Tabla 10 Parámetros de la modelación caso 2.
28
29
30
31
32
33
34
35
36
37
[°]
10
20
30
[°]
1,6
2
2,5
Sep. Entre perfiles [m]
En este caso los perfiles que se utilizaron para la modelación, son los que trae por
defecto el programa GGU-RETAIN. En la opción de calculo que ofrece el programa se
utilizó buscar el perfil óptimo para que el sistema comprendido por la geometría del
problema con los parámetros geotécnicos ya incluidos, sea el ideal en cuanto a
desplazamientos máximos, momentos flectores minimizados, acero de anclajes y longitud
de anclajes.
3.2.1 Procedimiento de iteración
Los siguientes son los pasos que se adoptaron para llegar a los resultados del
programa:
1. Se modela la geometría del problema con sus respectivas dimensiones en el
programa de ingeniería GGU-RETAIN .Esto se realiza solo una vez.
2. Se ingresan los datos geotécnicos para la primera iteración del muro.
3. La distancia entre perfiles, en este caso varía, por ende se deben hacer cuantas
iteraciones sea necesario.
4. Luego se adopta la forma en que determina el empuje activo y pasivo del
modelo. [5]
5. Se ingresa la carga distribuida al programa.
6. Luego se introducen los parámetros que tienen que ver con el anclaje.
Algunos son por defecto, ya que el programa iterará hasta encontrar el óptimo.
7. Se calcula el sistema y se procede a guardar la información obtenida para su
posterior análisis.
62
3.2.2 Resultados
A continuación se presentan los gráficos más importantes que se obtuvieron de la
modelación para un muro berlinés con una línea de anclaje.
Gráfico 3 Tipo de perfil HEB utilizado en la modelación para caso 2.
En la gráfica anterior se muestra que a medida que la separación entre perfiles
aumenta, el tamaño del perfil necesario para el muro berlinés también lo hará.
Se ha verificado que el ángulo θ, relativo a la inclinación del anclaje, no tiene mucho
que ver con la elección de dicho perfil.
63
Gráfico 4 Longitud de enterramiento del perfil de acero HEB utilizado para caso 2.
Del Gráfico 4 se desprende que la longitud de enterramiento del perfil no depende del
ángulo de inclinación del anclaje θ, sino que de la separación entre perfiles que se utiliza.
Además se denota que el ángulo de fricción interna del suelo también tiene una importancia
fundamental a la hora de condicionar el parámetro longitud de enterramiento, ya que a
menor ángulo de fricción interna del suelo, se necesitará una longitud de embebimiento
mayor para lograr el equilibrio estático requerido.
64
Gráfico 5 Desplazamiento horizontal máximo para caso 2.
Si bien el gráfico no es del todo clarificador, las series muestran puntos altos y bajos
los que se deben a que el programa GGU-RETAIN al estar trabajando bajo la condición de
optimizar los perfiles, éste evalúa en cada iteración el desplazamiento máximo entre otros
parámetros, por ende, los cambios de pendiente en las series se ven modificadas gracias a
los cambios de perfiles generados por el programa. Es claro ver que ningún valor del
desplazamiento horizontal máximo no sobrepasa los 10 mm. (Máximo 20 mm. [13]).
El ángulo de inclinación del anclaje θ, no incide mayormente en el valor del
desplazamiento horizontal máximo, siendo nuevamente el espaciamiento entre perfiles y el
ángulo de fricción interna φ los que gobiernan el desarrollo del desplazamiento.
65
Gráfico 6 Longitud de anclaje para caso 2.
Para el caso de la longitud de anclaje depende tanto del ángulo de inclinación del
anclaje θ, como de la separación entre perfiles.
Gráfico 7 Carga de anclaje para caso 2.
66
La carga del anclaje es gobernada por el ángulo de inclinación del anclaje θ, al igual
que la longitud de anclaje.
Gráfico 8 Espesor de ademes de madera caso 2.
La separación entre perfiles es el parámetro que maneja el comportamiento del
espesor de ademes de madera en el caso 2.
De esta forma queda totalmente analizado el caso de un muro berlinés con una línea
de anclaje distante 1,8 m. de la corona.
A continuación se presenta el último caso estudiado, el que se refiere a un muro
berlinés con dos líneas de anclajes.
67
3.3 Caso 3: Muro berlinés con dos líneas de anclaje
En esta oportunidad, el muro berlinés con dos líneas de anclaje se llevo a cabo con
una altura de excavación de 10 m., una línea de anclajes a 2,5 m. y la otra a 6,25 m. de la
corona del muro. También se desarrolla sobrecarga de
con un peso especifico de
. Para el suelo se cuenta
. El efecto de la napa no se considera en esta ocasión.
Muro Berlinés con 2 líneas de anclaje
2,5 m
P=10 KN/m²
3,75 m
Longitud de anclaje
óptima s/acero
Ѳ
Lm
3,75 m
10 m
Ѳ
Suelo
Φ=(variable 28°-37°)
Ѳ= (variable 10°, 20° y 30°)
C= 0 Kpa
γ=18 KN/m³
Perfil óptimo
Figura 36 Muro berlinés con dos líneas de anclajes.
Las variables que se harán variar serán cuatro, y se presentan a continuación:
1. Angulo de fricción interna del suelo,
2. Angulo de inclinación del anclaje y
3. Separación entre perfiles de acero.
La cohesión es nula, al igual que en el caso 2.
68
En la siguiente Tabla se muestran los valores que se adoptaron los parámetros
variables en la modelación:
Tabla 11 Parámetros de la modelación caso 3.
28
29
30
31
32
33
34
35
36
37
[°]
10
20
30
[°]
1,6
2
2,5
Sep. Entre perfiles [m]
En esta modelación se buscara estudiar las mismas variables que se hicieron en el
caso 2, pero en esta situación, se debe añadir la segunda línea de anclajes, la que tornara
más interesante el estudio.
3.3.1 Procedimiento de iteración
Los siguientes son los pasos que se adoptaron para llegar a los resultados del
programa:
1. Se modela la geometría del problema con sus respectivas dimensiones en el
programa de ingeniería GGU-RETAIN .Esto se realiza solo una vez.
2. Se ingresan los datos geotécnicos para la primera iteración del muro.
3. La distancia entre perfiles, en este caso varía, por ende se deben hacer cuantas
iteraciones sea necesario.
4. Luego se adopta la forma en que determina el empuje activo y pasivo del
modelo. [4]
5. Se ingresa la carga distribuida al programa.
6. Luego se introducen los parámetros que tienen que ver con los anclajes.
Algunos son por defecto, ya que el programa iterará hasta encontrar el óptimo.
7. Se calcula el sistema y se procede a guardar la información obtenida para su
posterior análisis.
69
3.3.2 Resultados
A continuación se presentan los gráficos más importantes que se obtuvieron de la
modelación para un muro berlinés con dos líneas de anclaje.
Gráfico 9 Tipo de perfil HEB utilizado en la modelación para caso 3.
Si se tomase una primera aproximación, se ve claramente que la influencia de la
separación entre perfiles es importante a la hora de variar el ángulo de fricción interna del
suelo testeado. Al igual que en el caso 2 se ha verificado que el ángulo θ, relativo a la
inclinación del anclaje, no influye en la elección del perfil
70
Gráfico 10 Longitud de enterramiento del perfil de acero HEB utilizado para caso 3.
Como sucedió en el caso 2, el ángulo de inclinación del anclaje θ no genera una
variación importante, por lo que se decidió incorporar en el Gráfico 10 solo las separación
entre perfiles como variable que decide el comportamiento de la longitud de enterramiento
a medida que se varia el ángulo de fricción interna del suelo φ.
71
Gráfico 11 Desplazamiento horizontal máximo para caso 3.
Del desplazamiento horizontal máximo, no se puede dar una aseveración muy
concluyente, ya que el programa es el que controla esta variable (al seleccionar el perfil
óptimo de uso). Si se puede mencionar que el programa para el caso de un muro con
anclajes y en situación óptima, siempre arroja valores de desplazamientos máximos
menores al propuesto por Oróstegui P. y Villalobos F. que es de 20 mm.
72
Para el caso de la longitud de anclajes, se presentan a continuación en tres gráficos
que contienen la longitud del anclaje superior e inferior por cada separación entre perfil
propuesto.
Gráfico 12 Longitud de anclajes para caso 3 con una separación entre perfiles de 1,6 m.
Gráfico 13 Longitud de anclajes para caso 3 con una separación entre perfiles de 2 m.
73
Gráfico 14 Longitud de anclajes para caso 3 con una separación entre perfiles de 2,5 m.
Lo que se puede apreciar de los gráficos 12, 13 y 14, es que la longitud de cada
anclaje está gobernada, mayormente por el ángulo de fricción interna del suelo φ y en un
grado menor por la inclinación del ángulo θ respectivo a la inclinación del anclaje. La línea
de anclaje superior es de mayor longitud que la línea de anclaje inferior.
74
Gráfico 15 Carga de anclajes para caso 3 con una separación entre perfiles de 1,6 m.
Gráfico 16 Carga de anclajes para caso 3 con una separación entre perfiles de 2 m.
75
Gráfico 17 Carga de anclajes para caso 3 con una separación entre perfiles de 2,5 m.
En los gráficos 15, 16 y 17 se muestra que a mayor separación entre perfiles, mayor
es la carga que toma cada anclaje. Así también es claro que la línea de anclaje inferior es la
que toma mayor carga.
76
Gráfico 18 Espesor de ademes de madera caso 3.
Como se observa en el Gráfico 18, el ángulo θ no produce un cambio en cuanto al
espesor de los tablones de madera. La variación se produce debido a la separación entre
perfiles, a razón de a mayor separación de perfiles de acero, mayor será el espesor del
tablón.
77
Capítulo 4
Conclusiones y Recomendaciones
78
4. Conclusiones y Recomendaciones
4.1 Conclusiones
Se modelaron tres configuraciones de muro Berlinés, sin anclaje, con uno y dos
anclajes, los cuales adoptan distintas geometrías y de este modo se analizó el
comportamiento de cada uno de ellos al ser sometidos a cambios en sus parámetros
geotécnicos. El primer caso corresponde a un muro berlinés sin anclaje, el que presentó
variados problemas con respecto a su desplazamiento horizontal máximo. Se piensa que
una carga de
es para condición crítica (ver [4]), lo cual es muy desfavorable a
la hora de evaluar el comportamiento del sistema de entibación, eso sí, muestra resultados
sobre desplazamientos horizontales excesivos, a pesar de que el sistema de contención
resiste y tiene aún suficiente capacidad. La restricción del desplazamiento horizontal
permite sólo realizar entibaciones de 4 m (caso estudiado) para altas cohesiones (mayores a
100 kPa) y ángulos de fricción mayores a 30º. En realidad se debe hacer un estudio
paramétrico para establecer la restricción de desplazamientos para cada caso, dado que se
producen cambios dependiendo de la combinatoria de valores de c y φ (ver anexo 3).
Se observa que para el sistema no anclado el ángulo de fricción suelo-muro δ/φ, el
ángulo de fricción interna del suelo φ y la cohesión son inversamente proporcionales a la
longitud de enterramiento presentada por el perfil de acero (Anexo 2). Dicho tipo de perfil
no tiene incidencia, en este caso, en la longitud embebida.
Además de la longitud de enterramiento, también se analizó el comportamiento del
desplazamiento horizontal máximo que ocurre en la corona del muro, para el tipo de
distribución de empujes que se utiliza. Así los parámetros δ/φ, φ, c y perfil de acero HN
también son inversamente proporcionales al desplazamiento máximo w (Anexo 3). En este
caso se logra evidenciar la importancia del uso de anclajes en muros con una altura de
79
excavación de 4 m. (caso estudiado), además de las condiciones del suelo son
importantísimas al evaluar el comportamiento del desplazamiento horizontal máximo.
Por ende, se recomienda monitorear permanentemente los desplazamientos
horizontales en base a inclinómetros ubicados en sitios estratégicos a lo largo del muro.
Esto es de vital importancia para que la entibación no genere o produzca daño, tales como
agrietamientos producto de asentamientos o desplazamientos, en construcciones vecinas a
la excavación.
Si se realiza un análisis conjunto de los casos con un anclaje (2) y con dos anclajes
(3), muros anclados, se puede concluir a partir del análisis de los gráficos 3 a 8 y 9 a 18,
que para ambos casos se tiene un comportamiento similar. Esto en base a los resultados de
separación de perfiles, longitud de enterramiento, desplazamiento horizontal máximo,
longitudes de anclaje, carga en los anclajes, inclinación del anclaje y espesor de ademes.
Para los parámetros estudiados se concluye que:
-
Para el perfil HEB, a mayor separación entre perfiles, mayor es el tamaño del
perfil final. El ángulo de inclinación del anclaje θ no tiene incidencia en los
resultados obtenidos por el programa GGU-RETAIN, mientras que a mayor
φ, menor será el tamaño del perfil HEB.
-
En el caso de la longitud de enterramiento, a mayor separación entre perfiles,
mayor es la longitud de enterramiento L (m). Nuevamente θ no incide en este
parámetro y el ángulo de fricción interna del suelo φ es inversamente
proporcional a L (m).
-
En cuanto al desplazamiento horizontal máximo se concluye que al ser
incorporado un anclaje al muro, éste controla completamente el problema de
desplazamientos horizontales excesivos. Se logra identificar que el valor
máximo del desplazamiento horizontal extraído de las modelaciones con
GGU-RETAIN para los casos de sistemas anclados es de 12 mm.
80
-
La longitud del anclaje también fue analizada, llegando a concluir que la
separación entre perfiles s, es directamente proporcional y tanto θ como φ son
inversamente proporcionales a la longitud de los anclajes. Se observa que para
el caso 3 la línea de anclaje superior es de mayor longitud que la línea de
anclaje inferior.
-
Para la carga del anclaje, en el caso 2 se infiere que no depende de la
separación entre perfiles sino que del ángulo de inclinación del anclaje θ,
siendo directamente proporcional con la carga que recibe el anclaje. El ángulo
de fricción interna del suelo φ es inversamente proporcional a la carga del
anclaje. Para el caso 3 si se denota que la separación entre perfiles es
directamente proporcional, al igual que el ángulo de inclinación del anclaje θ.
El ángulo de fricción interna del suelo φ es inversamente proporcional a la
carga que reciben los anclajes. La línea inferior de anclajes es la que toma
más carga en esta ocasión.
-
Por último, el espesor de los ademes de madera que cubren la pantalla de la
entibación no dependen de θ, si del ángulo de fricción interna del suelo φ, la
que es inversamente proporcional. Mientras que la separación entre perfiles de
acero es directamente proporcional al espesor de los tablones de madera.
Finalmente, y con todo lo expuesto anteriormente, se recomienda realizar ensayos
geotécnicos a los anclajes para verificar los parámetros de diseño. Las entibaciones del tipo
muro berlinés al ser flexibles pueden presentar variaciones importante en los resultados
incluso al ser sometidos a pequeños cambios en sus parámetros de diseño. Estos cambios
están relacionados con desplazamientos horizontales excesivos (no deseados) y longitudes
de enterramiento y secciones del perfil mayores, los que aumentan el costo final del
proyecto en el caso de sobredimensionar los parámetros geotécnicos. Por otro lado, si los
parámetros geotécnicos son determinados con un alto nivel de confianza, es decir, se cuenta
con una base suficiente de datos de buena calidad obtenida de ensayos in situ y en
81
laboratorio, es posible reducir costos del proyecto de entibación. El peor caso sería usar
valores de parámetros geotécnicos muy por debajo de los valores más probables y que
incluso los factores de seguridad no pueden cubrir en ciertos estados de carga muy
desfavorables. Esta situación pone en riesgo no sólo la integridad de la obra y la de las
estructuras vecinas sino también la vida de la personas.
4.2 Recomendaciones
Como se mencionó anteriormente, contar con un sistema de monitoreo en la obra es
de vital importancia, ya que se cuenta con información detallada y al instante del
comportamiento del muro berlinés (Correia et al. 1997). Además, es una herramienta muy
valiosa a la hora de poder realizar modelos de comportamiento de muros y de esta manera
tener un parámetro tangible del comportamiento de los suelos en la zona de Concepción.
Otra recomendación que se puede hacer es la que respecta a la distribución de
empujes detrás del muro. En mecánica de suelos, generalmente, se presenta la distribución
de empujes clásica, la que en este caso no funciona a la hora de evaluar muros anclados.
Por lo tanto, se recomienda revisar con mayor detalle este punto a la hora de efectuar
sistemas de entibación.
El uso de programas de Ingeniería es muy importante a la hora de realizar un trabajo
como este, ya que presenta la información de forma rápida, clara y sencilla. Se recomienda
utilizar el software de Ingeniería GGU-RETAIN para el caso de evaluar sistemas de
entibación.
82
4.3 Líneas futuras de investigación
Sería interesante conocer un estudio como el presentado al ser sometido a varios
estratos de suelo. Además, realizar un estudio mas acabado de la cohesión del suelo.
Otro parámetro importante que no se analizó es con respecto al costo. Conocer el
costo de este sistema sería importante a la hora de comparar con otros tipos de sistemas de
entibación como por ejemplo muros pantalla.
Se recomienda utilizar modelos de cálculo que permitan determinar la deformación
del suelo. Por ejemplo, usando programas de elementos finitos.
83
Bibliografía
84
5. Bibliografía
[1] CORREIA, A.G., da COSTA GUERRA, N.M. and PINTO, A. Performance of three
Berlin-type retaining walls. Proceeding of the fourteenth International Conference
on Soils Mechanics and Foundation Engineering, Vol. 2, 1297-1300, 1997.
[2] CRAIG, R.F. Craig’s soil mechanics. 7ª ed. Taylor & Francis Group, 2004.
[3] DAS, B. M. Principios de ingeniería de cimentaciones, 4º ed., International
Thomson Editores, 2001.
[4] DEUTSCHE gesellschaft für geotechnik e. v. Recommendations on Excavations
(EAB), 2ª ed. Ernst & Sohn, 2008.
[5] DIN 4085. Baugrund- Berechniung des erddrucks. 2007.
[6] DIN 4125. Ground anchorages: Design, construction and testing. 1990.
[7] DIN 1054. Subsoil: Permissible loading of subsoil. 1976.
[8] EGAN, D. The ground: clients remain exposed to unnecessary risk. Geotechnical
Engineering. (161), 189-195, 2008.
[9] FHWA-IF-99-015. Ground Anchors and Anchored Systems. U.S. Department of
Transportation, 1999.
[10] GGU-RETAIN. Análisis y diseño de muros pantalla de hormigón in situ,
tablestacados metálicos y tablestacados mediante costillas y ademes. 4ª ed. 2007.
[11] MURTHY V.N.S. Geotechnical Engineering, Principies and practices of soil
mechanics and foundation engineering. 1ª ed. New York, Macel Dekker Inc.
85
[12] NCH 3206. Geotecnia- Excavaciones, entibaciones y socalzados – Requisitos.
2010.
[13] OROSEGUI, P. y VILLALOBOS, F. Diseño y construcción de las entibaciones
para los estacionamientos subterráneos de los tribunales de justicia de Concepción.
Obras y Proyectos (6) 63-71, 2010.
[14] SOWERS, G.B. y SOWERS, G.F. Introducción a la mecánica de suelos y
cimentaciones. Limusa Wiley, 1972.
[15] TERZAGHI, K., y PECK, R. Soil mechanics in engineering practice. John Wiley
& Sons Inc, 1967.
[16] TERZAGHI, K., PECK, R., MESRI, G. Soil mechanics in engineering practice. 3ª
ed. John Wiley & Sons Inc, 1996.
86
ANEXOS
Tablas y Salidas del Programa
87
6. Tablas
88
δ/φ=0,5
δ/φ=0,667
δ/φ=1
C (kPa)
φ=10° φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
17,07
12,26
8,9
6,73
4,93
2,88
17,07
12,26
8,9
6,73
4,93
2,88
17,07
12,26
8,9
6,73
4,93
2,88
11,18
8,06
6,25
4,69
3,49
2,04
11,18
8,06
6,25
4,69
3,49
2,04
11,18
8,06
6,25
4,69
3,49
2,04
7,33
5,41
4,32
3,24
2,4
1,44
7,33
5,41
4,32
3,24
2,4
1,44
7,33
5,41
4,32
3,24
2,4
1,44
4,68
3,72
2,88
2,16
1,68
0,96
4,68
3,72
2,88
2,16
1,68
0,96
4,68
3,72
2,88
2,16
1,68
0,96
3,96
3
2,28
1,8
1,32
0,84
3,96
3
2,28
1,8
1,32
0,84
3,96
3
2,28
1,8
1,32
0,84
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
C (kPa)
φ=10° φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
16,77
11,98
8,75
6,59
4,79
2,76
16,77
11,98
8,75
6,59
4,79
2,76
16,77
12,26
8,9
6,73
4,93
2,88
10,94
7,69
6,01
4,57
3,36
1,92
10,94
7,69
6,01
4,57
3,36
1,92
10,94
7,69
6,01
4,57
3,36
1,92
6,97
5,17
3,96
3,12
2,28
1,32
6,97
5,17
3,96
3,12
2,28
1,32
6,97
5,17
3,96
3,12
2,28
1,32
4,32
3,48
2,64
2,04
1,56
0,96
4,32
3,48
2,64
2,04
1,56
0,96
4,32
3,48
2,64
2,04
1,56
0,96
3,48
2,76
2,16
1,68
1,2
0,84
3,48
2,76
2,16
1,68
1,2
0,84
3,48
2,76
2,16
1,68
1,2
0,84
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
C (kPa)
φ=10° φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
16,3
11,63
8,39
6,47
4,68
2,64
16,3
11,63
8,39
6,47
4,68
2,64
16,3
12,26
8,9
6,73
4,93
2,88
10,34
7,33
5,65
4,33
3,12
1,92
10,34
7,33
5,65
4,33
3,12
1,92
10,34
7,33
5,65
4,33
3,12
1,92
6,47
4,8
3,72
2,88
2,04
1,32
6,47
4,8
3,72
2,88
2,04
1,32
6,47
4,8
3,72
2,88
2,04
1,32
4,32
3,24
2,52
1,92
1,44
0,84
4,32
3,24
2,52
1,92
1,44
0,84
4,32
3,24
2,52
1,92
1,44
0,84
3,6
2,76
2,04
1,56
1,2
0,72
3,6
2,76
2,04
1,56
1,2
0,72
3,6
2,76
2,04
1,56
1,2
0,72
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
ANEXO 1 Analisis de sensibilidad factor /
(ángulo de fricción suelo-muro). Valores para la longitud de enterramiento del muro (m) caso 1.
89
PARA TODOS LOS PERFILES
C (kPa)
c=0
c=10
c=25
c=50
c=100
c=300
Relación suelo-muro
φ=10°
17,07
12,26
8,9
6,73
4,93
2,88
δ/φ=0,5
φ=10°
16,77
11,98
8,75
6,59
4,79
2,76
δ/φ=0,667
φ=10°
16,3
11,63
8,39
6,47
4,68
2,64
δ/φ=1
φ=20°
11,18
8,06
6,25
4,69
3,49
2,04
δ/φ=0,5
φ=20°
10,94
7,69
6,01
4,57
3,36
1,92
δ/φ=0,667
φ=20°
10,34
7,33
5,65
4,33
3,12
1,92
δ/φ=1
φ=30°
7,33
5,41
4,32
3,24
2,4
1,44
δ/φ=0,5
φ=30°
6,97
5,17
3,96
3,12
2,28
1,32
δ/φ=0,667
φ=30°
6,47
4,8
3,72
2,88
2,04
1,32
δ/φ=1
φ=40°
4,68
3,72
2,88
2,16
1,68
0,96
δ/φ=0,5
φ=40°
4,32
3,48
2,64
2,04
1,56
0,96
δ/φ=0,667
φ=40°
4,32
3,24
2,52
1,92
1,44
0,84
δ/φ=1
φ=45°
3,96
3
2,28
1,8
1,32
0,84
δ/φ=0,5
φ=45°
3,48
2,76
2,16
1,68
1,2
0,84
δ/φ=0,667
φ=45°
3,6
2,76
2,04
1,56
1,2
0,72
δ/φ=1
ANEXO 2 Longitud de enterramiento para el caso 1.
90
δ/φ=0,5
δ/φ=0,667
δ/φ=1
C (kPa)
φ=10°
φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
2875,5
891,7
377,8
223,4
136,1
69,6
951,5
295,1
125
73,9
45
23
393,5
122
51,7
30,6
18,6
9,5
734,6
265,1
158,3
99,9
67,1
38,6
243,1
87,7
52,4
33
22,2
12,8
100,5
36,3
21,7
13,7
9,2
5,3
213,9
103,5
72,3
49,4
35,5
23,2
70,8
34,2
23,9
16,3
11,7
7,7
29,3
14,2
9,9
6,8
4,9
3,2
69,2
47,6
34,2
25,3
20,3
14,1
22,9
15,8
11,3
8,4
6,7
4,7
9,5
6,5
4,7
3,5
2,8
1,9
48,4
32,4
23,7
19
15
11,5
16
10,7
7,8
6,3
4,9
3,8
6,6
4,4
3,2
2,6
2
1,6
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
C (kPa)
φ=10°
φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
2672,6
826,8
357,3
210,6
127,8
64,8
884,4
273,6
118,2
69,7
42,3
21,5
393,5
113,1
48,9
28,8
17,5
8,9
679,2
232,9
142,6
92,5
61,9
35,3
224,7
77,1
47,2
30,6
20,5
11,7
92,9
31,9
19,5
12,7
8,5
4,8
184
91,5
61,1
45
32,2
20,9
60,9
30,3
20,2
14,9
10,7
6,9
25,2
12,5
8,4
6,2
4,4
2,9
55,7
42
30
23,1
18,5
13,6
20,2
13,9
9,9
7,7
6,1
4,5
8,3
5,7
4,1
3,2
2,5
1,9
33,5
28,4
21,7
17,4
13,6
11,2
14,2
9,4
7,2
5,7
4,5
3,7
5,9
3,9
3
2,4
1,9
1,5
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
C (kPa)
φ=10°
φ=10° φ=10° φ=20° φ=20° φ=20° φ=30° φ=30° φ=30° φ=40° φ=40° φ=40° φ=45° φ=45° φ=45°
C=0
C=10
C=25
C=50
C=100
C=300
2371
735,9
313,6
193,8
116,8
58,6
784,7
243,5
103,8
64,1
38,7
19,4
324,5
100,7
42,9
26,5
16
8
544,9
198,2
120,5
80,1
53
32,9
180,3
65,6
39,9
26,5
17,5
10,9
74,6
27,1
16,5
11
7,2
4,5
146,1
75,9
52,2
38,2
27
19,4
48,3
25,1
17,3
12,6
8,9
6,4
20
10,4
7,1
5,2
3,7
2,7
54,6
35,7
26,5
20,4
16,1
11,8
18,1
11,8
8,8
6,7
5,3
3,9
7,5
4,9
3,6
2,8
2,2
1,6
38
26,5
19,2
15,3
12,7
9,7
12,6
8,8
6,4
5,1
4,2
3,2
5,2
3,6
2,6
2,1
1,7
1,3
PERFIL HN
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
30X180
40X301
50X462
ANEXO 3 Analisis de sensibilidad factor /
(ángulo de fricción suelo-muro). Valores para el desplazamiento del muro (mm) caso 1.
91
Sep. entre perfiles (m)
2,5 m
2m
1,6 m
Ѳanclaje=10°
φ°=28
240
φ°=29
240
φ°=30
240
φ°=31
220
φ°=32
220
φ°=33
220
φ°=34
220
φ°=35
220
φ°=36
200
φ°=37
200
Ѳanclaje=20°
240
240
240
220
220
220
220
220
200
200
Ѳanclaje=30°
240
240
240
240
220
220
220
220
220
200
Ѳanclaje=10°
220
220
220
200
200
200
200
200
180
180
Ѳanclaje=20°
220
220
220
200
200
200
200
200
200
180
Ѳanclaje=30°
220
220
220
220
200
200
200
200
200
180
Ѳanclaje=10°
200
200
200
180
180
180
180
180
180
160
Ѳanclaje=20°
200
200
200
200
180
180
180
180
180
180
Ѳanclaje=30°
200
200
200
200
180
180
180
180
180
180
φ°=33
3,24
3,24
3,24
3,00
3,00
3,00
2,88
2,88
2,88
φ°=34
3,00
3,12
3,12
2,88
2,88
2,88
2,76
2,76
2,76
φ°=35
2,88
2,88
2,88
2,76
2,76
2,76
2,64
2,64
2,64
φ°=36
2,88
2,88
2,76
2,64
2,64
2,64
2,52
2,52
2,52
φ°=37
2,76
2,76
2,76
2,52
2,52
2,52
2,40
2,40
2,40
Ѳanclaje
ANEXO 4 Perfiles de acero HEB óptimos para caso 2.
Separación entre perfiles (m)
2,5 m
2m
1,6 m
Ѳanclaje
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
φ°=28
3,84
3,96
3,96
3,72
3,72
3,72
3,48
3,48
3,48
φ°=29
3,72
3,72
3,72
3,48
3,48
3,48
3,36
3,36
3,36
φ°=30
3,60
3,60
3,60
3,36
3,36
3,36
3,24
3,24
3,24
φ°=31
3,48
3,48
3,48
3,24
3,24
3,24
3,12
3,00
3,12
φ°=32
3,36
3,36
3,36
3,12
3,12
3,12
3,00
3,00
3,00
ANEXO 5 Longitud de enterramiento del perfil de acero (m) para caso 2.
92
Separación entre perfiles (m)
2,5 m
2m
1,6 m
Ѳanclaje
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
φ°=28
10,40
8,95
8,12
10,25
8,82
8,01
10,10
8,69
7,89
φ°=29
9,89
8,54
7,78
9,75
8,42
7,67
9,60
8,30
7,56
φ°=30
9,41
8,17
7,46
9,27
8,05
7,35
9,13
7,93
7,24
φ°=31
9,09
7,92
7,15
8,82
7,69
7,04
8,69
7,57
6,94
φ°=32
8,65
7,57
6,96
8,52
7,46
6,85
8,39
7,57
6,75
φ°=33
8,24
7,24
6,68
8,12
7,13
6,57
7,99
7,02
6,48
φ°=34
7,85
6,93
6,40
7,73
6,82
6,31
7,61
6,72
6,21
φ°=35
7,48
6,63
6,15
7,36
6,52
6,05
7,25
6,42
5,96
φ°=36
7,24
6,44
5,90
7,12
6,24
5,80
7,01
6,24
5,80
φ°=37
6,90
6,16
5,75
6,79
6,06
5,66
6,68
5,96
5,57
φ°=28
7,1
7,1
7,2
7,2
7,3
7,4
7,6
7,6
7,7
φ°=29
6,4
6,4
6,5
6,5
6,6
6,7
6,8
6,9
7
φ°=30
5,8
5,8
5,9
5,9
6
6
6,2
6,2
6,3
φ°=31
7,4
7,4
5,3
7,7
7,8
5,5
8,5
5,6
5,7
φ°=32
6,7
6,7
6,8
7
7
7,1
7,7
7,7
7,8
φ°=33
6
6,1
6,1
6,3
6,3
6,4
6,9
7
7
φ°=34
5,4
5,4
5,5
5,7
5,7
5,8
6,3
6,4
6,7
φ°=35
4,9
4,9
5
5,1
5,2
5,4
6,3
6,4
6,7
φ°=36
6,3
6,4
4,6
7,3
5,2
5,4
6,3
6,4
6,6
φ°=37
5,8
6
6,3
7,3
7,5
7,7
9,4
6,3
6,6
ANEXO 6 Longitud de anclaje (m) para caso 2.
Separación entre perfiles (m)
2,5 m
2m
1,6 m
Ѳanclaje
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
ANEXO 7 Desplazamiento horizontal máximo del muro (mm) para caso 2.
93
Separación entre perfiles (m)
2,5 m
2m
1,6 m
Ѳanclaje
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
Ѳanclaje=10°
Ѳanclaje=20°
Ѳanclaje=30°
φ°=28
9,4
9,4
9,4
7,5
7,5
7,5
6
6
6
φ°=29
9,2
9,2
9,2
7,4
7,4
7,4
5,9
5,9
5,9
φ°=30
9
9
9
7,2
7,2
7,2
5,8
5,8
5,8
φ°=31
8,8
8,8
8,8
7,1
7,1
7,1
5,7
5,7
5,7
φ°=32
8,6
8,6
8,6
6,9
6,9
6,9
5,5
5,5
5,5
φ°=33
8,5
8,5
8,5
6,8
6,8
6,8
5,4
5,4
5,4
φ°=34
8,3
8,3
8,3
6,6
6,6
6,6
5,3
5,3
5,3
φ°=35
8,1
8,1
8,1
6,5
6,5
6,5
5,2
5,2
5,2
φ°=36
7,9
7,9
7,9
6,3
6,3
6,3
5,1
5,1
5,1
φ°=37
7,7
7,7
7,7
6,2
6,2
6,2
4,9
4,9
4,9
ANEXO 8 Espesor de ademes de madera (cm) para caso 2.
94
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
240
10,4
110,7
220,1
46
57,3
63,9
7,1
-0,11
9,4
3,84
240
9,89
105,26
210,5
44,1
54,7
62,8
6,4
-0,12
9,2
3,72
240
9,41
100,64
201,3
42,2
52,2
61,8
5,8
-0,12
9
3,6
220
9,09
96,26
192,5
40,5
49,9
60,4
7,4
-0,17
8,8
3,48
220
8,65
91,99
184
38,7
47,6
59,3
6,7
-0,17
8,6
3,36
220
8,24
87,89
175,8
37,1
45,4
58,2
6
-0,17
8,5
3,24
220
7,85
83,94
167,9
35,5
43,2
57
5,4
-0,17
8,3
3
220
7,48
80,14
160,3
33,9
41,2
55,9
4,9
-0,17
8,1
2,88
200
7,24
76,54
153,1
32,4
39,3
54,5
6,3
-0,24
7,9
2,88
200
6,9
73,03
146,1
31
37,5
53,3
5,8
-0,24
7,7
2,76
Ѳanclaje=10°
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
Perfil necesario HEB
220
10,25
109,77
219,5
46
57
64
7,2
-0,14
7,5
3,72
220
9,75
104,98
210
44,1
54,4
62,9
6,5
-0,14
7,4
3,48
220
9,27
100,38
200,8
42,2
51,9
61,9
5,9
-0,14
7,2
3,36
200
8,82
96,2
192
40,5
49,6
60,5
7,7
-0,2
7,1
3,24
200
8,52
91,77
183,5
38,7
47,3
59,4
7
-0,2
6,9
3,12
200
8,12
87,68
175,4
37,1
45,2
58,3
6,3
-0,21
6,8
3
200
7,73
83,75
167,5
35,5
43,1
57,1
5,7
-0,21
6,6
2,88
200
7,36
79,97
159,9
33,9
41,1
56
5,1
-0,2
6,5
2,76
180
7,12
76,38
152,8
32,4
39,52
54,5
7,3
-0,3
6,3
2,64
180
6,79
72,88
145,8
31
37,3
53,3
7,3
-0,3
6,2
2,52
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
200
10,1
109,49
219
46
56,7
64,1
7,6
-0,17
6
3,48
200
9,6
104,71
209,4
44,1
54,1
63,1
6,8
-0,17
5,9
3,36
200
9,13
100,13
200,3
42,2
51,7
62
6,2
-0,18
5,8
3,24
180
8,69
95,8
191,6
40,5
49,4
60,5
8,5
-0,26
5,7
3,12
180
8,39
91,56
183,1
38,7
47,1
59,4
7,7
-0,26
5,5
3
180
7,99
87,48
175
37,1
45
58,3
6,9
-0,26
5,4
2,88
180
7,61
83,57
167,1
35,5
42,9
57,2
6,3
-0,26
5,3
2,76
180
7,25
79,8
159,6
33,9
40,9
56
6,3
-0,25
5,2
2,64
180
7,01
76,17
152,3
32,4
39
54,9
6,3
-0,25
5,1
2,52
160
6,68
72,74
145,5
31
37,2
53,4
9,4
-0,38
4,9
2,4
separación de perfiles de 2m
separación de perfiles de 2,5 m
Ѳanclaje=10°
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
separación de perfiles de 1,6m
Ѳanclaje=10°
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
ANEXO 9 Tabla de salida para θ=10°, ángulo de inclinación del anclaje caso 2.
95
separación de perfiles de 2,5 m
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
separación de perfiles de 2m
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
separación de perfiles de 1,6m
Ѳanclaje=20°
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
Ѳanclaje=20°
Ѳanclaje=20°
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
240
8,95
115,34
230,7
46
57,2
84,2
7,1
-0,11
9,4
3,96
240
8,54
110,3
220,6
44,1
54,7
82,3
6,4
-0,12
9,2
3,72
240
8,17
105,46
210,9
42,2
52,2
80,4
5,8
-0,12
9
3,6
220
7,92
100,87
201,7
40,5
49,8
78,2
7,4
-0,17
8,8
3,48
220
7,57
96,4
192,8
38,7
47,6
76,3
6,7
-0,17
8,6
3,36
220
7,24
92,1
184,2
37,1
45,4
74,4
6,1
-0,17
8,5
3,24
220
6,93
87,96
175,9
35,5
43,2
72,5
5,4
-0,17
8,3
3,12
220
6,63
83,98
168
33,9
41,2
70,7
4,9
-0,17
8,1
2,88
200
6,44
80,21
160,4
32,4
39,3
68,6
6,4
-0,24
7,9
2,88
200
6,16
76,53
153,1
31
37,5
66,8
6
-0,24
7,7
2,76
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
220
8,82
115,03
230,1
46
57
84,3
7,3
-0,14
7,5
3,72
220
8,42
110,01
220
44,1
54,4
82,3
6,6
-0,14
7,4
3,48
220
8,05
105,18
210,4
42,2
51,9
80,4
6
-0,15
7,2
3,36
200
7,69
100,62
201,2
40,5
49,6
78,2
7,8
-0,2
7,1
3,24
200
7,46
96,16
192,3
38,7
47,3
76,3
7
-0,21
6,9
3,12
200
7,13
91,88
183,8
37,1
45,1
74,5
6,3
-0,21
6,8
3
200
6,82
87,76
175,5
35,5
43,1
72,6
5,7
-0,21
6,6
2,88
200
6,52
83,8
167,6
33,9
41
70,7
5,2
-0,21
6,5
2,76
200
6,24
79,99
160
32,4
39,1
68,9
5,2
-0,2
6,3
2,64
180
6,06
76,37
152,7
31
37,3
66,8
7,5
-0,3
6,2
2,52
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
200
8,69
114,73
229,5
46
56,7
84,3
7,6
-0,17
6
3,48
200
8,3
109,73
219,5
44,1
54,1
82,4
6,9
-0,18
5,9
3,36
200
7,93
104,93
209,9
42,2
51,7
80,5
6,2
-0,18
5,8
3,24
200
7,57
100,31
200,6
40,5
49,3
78,6
5,6
-0,18
5,7
3
180
7,57
95,95
191,9
38,7
47,1
76,3
7,7
-0,26
5,5
3
180
7,02
91,68
183,4
37,1
45
74,5
7
-0,26
5,4
2,88
180
6,72
87,57
175,1
35,5
42,9
72,6
6,4
-0,26
5,3
2,76
180
6,42
83,62
167,2
33,9
40,9
70,8
6,4
-0,26
5,2
2,64
180
6,24
79,83
159,7
32,4
39
68,9
6,4
-0,25
5,1
2,52
180
5,96
76,17
152,3
31
37,1
67,1
6,3
-0,25
4,9
2,4
ANEXO 10 Tabla de salida para θ=20°, ángulo de inclinación del anclaje caso 2.
96
separación de perfiles de 2,5 m
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
separación de perfiles de 2m
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
separación de perfiles de 1,6m
Ѳanclaje=30°
Perfil necesario HEB
Longitud anclaje (m)
Fuerza Normal (KN)
Carga de Anclaje disp [kN]
Momento máximo(KN m/m)
Fuerza de corte máxima(KN/m)
Fuerza normal máxima(KN/m)
Desplazamiento máximo (mm)
Rotación de la corona del muro(°)
Espesor óptimo de ademes(cm)
Profundidad de embebimiento(m)
Ѳanclaje=30°
Ѳanclaje=30°
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
240
8,12
125,13
250,3
46
57,2
107,3
7,2
-0,12
9,4
3,96
240
7,78
119,66
239,3
44,1
54,6
104,4
6,5
-0,12
9,2
3,72
240
7,46
114,41
228,8
42,2
52,1
101,5
5,9
-0,12
9
3,6
240
7,15
109,36
218,7
40,5
49,8
98,7
5,3
-0,13
8,8
3,48
220
6,96
104,58
209,2
38,7
47,5
95,6
6,8
-0,17
8,6
3,36
220
6,68
99,91
199,8
37,1
45,3
92,9
6,1
-0,17
8,5
3,24
220
6,4
95,42
190,8
35,5
43,2
90,2
5,5
-0,18
8,3
3,12
220
6,15
91,11
182,2
33,9
41,2
87,5
5
-0,18
8,1
2,88
220
5,9
86,96
173,9
32,4
39,3
84,9
4,6
-0,17
7,9
2,76
200
5,75
83,02
166
31
37,4
82,1
6,3
-0,24
7,7
2,76
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
220
8,01
124,8
249,6
46
56,9
107,3
7,4
-0,14
7,5
3,72
220
7,67
119,35
238,7
44,1
54,4
104,4
6,7
-0,15
7,4
3,48
220
7,35
114,11
228,2
42,2
51,9
101,5
6
-0,15
7,2
3,36
220
7,04
109,09
218,2
40,5
49,5
98,7
5,5
-0,15
7,1
3,24
200
6,85
104,33
208,7
38,7
47,3
95,6
7,1
-0,21
6,9
3,12
200
6,57
99,68
199,4
37,41
45,1
92,9
6,4
-0,21
6,8
3
200
6,31
95,21
190,4
35,5
43
90,2
5,8
-0,21
6,6
2,88
200
6,05
90,91
181,8
33,9
41
87,5
5,4
-0,21
6,5
2,76
200
5,8
86
173,6
32,4
39,1
84,9
5,4
-0,21
6,3
2,64
180
5,66
82,85
165,7
31
37,3
82,1
7,7
-0,3
6,2
2,52
φ°=28
φ°=29
φ°=30
φ°=31
φ°=32
φ°=33
φ°=34
φ°=35
φ°=36
φ°=37
200
7,89
124,48
249
46
56,7
107,3
7,7
-0,18
6
3,48
200
7,56
119,05
238,1
44,1
54,1
104,4
7
-0,18
5,9
3,36
200
7,24
113,84
227,7
42,2
51,7
101,5
6,3
-0,18
5,8
3,24
200
6,94
108,83
217,7
40,5
49,3
98,7
5,7
-0,18
5,7
3,12
180
6,75
104,1
208,2
38,7
47,1
95,6
7,8
-0,26
5,5
3
180
6,48
99,46
198,9
37,1
44,9
92,8
7
-0,26
5,4
2,88
180
6,21
95,01
190
35,5
42,9
90,2
6,7
-0,26
5,3
2,76
180
5,96
90,72
181,4
33,9
40,9
87,5
6,7
-0,26
5,2
2,64
180
5,8
86,6
173,2
32,4
39
84,9
6,6
-0,26
5,1
2,52
180
5,57
82,64
165,3
31
37,1
82,4
6,6
-0,25
4,9
2,4
ANEXO 11 Tabla de salida para θ=30°, ángulo de inclinación del anclaje caso 2.
97
Separación entre perfiles 2,5 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 5 [m]
Ángulo de anclaje
Ѳ=10[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
240
240
240
240
220
220
220
220
200
200
15,99
12,48
12,09
11,58
11,09
10,62
10,17
10,17
9,46
9,07
117,8
113
108,5
104
99,77
95,66
91,67
87,82
84,05
80,45
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 835/10 835/10
Acero seleccionado 770 5 770 5 770 5 770 5 770 4
30
30
litzen litzen litzen litzen litzen diámetro diámetro
36
36
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
589
565,4 542,6 520,2 498,9 478,3 458,4
[KN]
Longitud anclaje
9,7
10,72
10,3
9,78
9,3
8,83
8,39
[m]
Fuerza Normal
163,5
156
148,7
142
135,3
129
122,8
[KN/m]
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1
Acero seleccionado 770 7 770 7 770 6 770 6 770 6 770 6 770 5
litzen litzen litzen litzen litzen litzen litzen
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
817,9 780,1 743,8 710,2 676,9
645
614,4
[KN]
Momento Máx
62,1
58,7
55,5
52,8
49,9
47,2
44,6
[KN-m/m]
Fuerza Corte Máx
82,3
78,4
74,6
71,1
67,6
64,3
61,1
[KN/m]
Fuerza Normal
155,1 152,5 149,8 146,6 143,8
141
138,2
Máx [KN/m]
Desp. Máx [mm]
9
8,3
7,6
7
8,9
8,2
7,5
Espesor ademes
11
10,8
10,6
10,3
10,1
9,9
9,7
[cm]
Prof. Enterramiento
3,72
3,6
3,48
3,36
3,24
3,12
3
[m]
St
St
St
835/10 835/10 835/10
30
30
30
diámetro diámetro diámetro
36
36
36
439,1
420,2
402,2
8,39
7,69
7,31
117
111,5
106,1
St
St
St
1570/1 1570/1 1570/1
770 5 770 5 770 5
litzen litzen litzen
0,6''
0,6''
0,6''
585,1
557,9
530,9
42,2
40,1
37,9
58,1
55,3
52,5
135,3
132
129,1
6,8
8,9
8,2
9,5
9,3
9,1
2,76
2,76
2,64
ANEXO 12 Tabla de salida para =10° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2,5 m. Caso 3.
98
Separación entre perfiles 2 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 4 [m]
Ángulo de anclaje
Ѳ=10[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
220
220
220
200
200
200
200
200
180
180
15,85
12,33
11,8
11,44
10,95
10,49
10,05
9,75
9,34
9,07
118
113,3
108,7
104,2
99,97
95,84
91,84
87,97
84,19
80,58
St
St
St
St
St
St
St
835/10 835/10 835/10 835/10 835/10 835/10 1570/1
Acero seleccionado
770 3
30
30
30
30
30
30
diámetro diámetro diámetro diámetro diámetro diámetro litzen
36
36
36
36
36
32
0,6''
Carga anclaje disp
472,3 453,3
435
417
399,9 383,3 367,4
[KN]
Longitud anclaje
9,54
10,58 10,04
9,65
9,17
8,71
8,27
[m]
Fuerza Normal
162,5
155
147,8 141,2 134,6 128,3 122,2
[KN/m]
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1080/1
Acero seleccionado 770 6 770 5 770 5 770 5 770 5 770 5
230
litzen litzen litzen litzen litzen litzen diámetro
32
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
650,4 620,4 591,6
565
538,5 513,2 488,9
[KN]
Momento Máx
61
57,8
54,7
52
49,2
46,5
44
[KN-m/m]
Fuerza Corte Máx
81,6
77,7
74
70,5
67,1
63,8
60,7
[KN/m]
Fuerza Normal
155,2 152,6 149,9 146,7 143,9 141,1 138,3
Máx [KN/m]
Desp. Máx [mm]
9,4
8,6
7,9
10,4
9,5
8,7
8
Espesor ademes
8,8
8,6
8,5
8,3
8,1
7,9
7,7
[cm]
Prof. Enterramiento
3,6
3,36
3,24
3,12
3
2,88
2,76
[m]
St
St
St
1570/1 1080/1 1080/1
770 3
230
230
litzen diámetro diámetro
26,5
26,5
0,6''
351,9
336,7
322,3
7,97
7,58
7,3
116,4
111
105,6
St
St
St
835/10 835/10 835/10
30
30
30
diámetro diámetro diámetro
36
36
36
465,7
444,1
422,6
41,6
39,5
37,4
57,7
54,9
52,2
135,4
132,1
129,1
7,3
10,1
9,2
7,6
7,4
7,2
2,64
2,64
2,52
ANEXO 13 Tabla de salida para =10° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2 m. Caso 3.
99
Separación entre perfiles 1,6 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 3,2 [m]
Ángulo de anclaje
Ѳ=10[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
200
200
200
180
180
180
180
180
160
160
12,74
12,18
11,66
11,3
10,82
10,36
10,05
9,63
9,22
8,95
118,3
113,5
108,9
104,4
100,1
96
91,99
88,11
84,31
80,69
St
St
835/10 1570/1
Acero seleccionado
770 3
30
diámetro litzen
32
0,6''
Carga anclaje disp
378,7 363,4
[KN]
Longitud anclaje
11,01 10,44
[m]
Fuerza Normal
161,6 154,2
[KN/m]
St
St
1570/1 1080/1
Acero seleccionado 770 5
230
litzen diámetro
32
0,6''
Carga anclaje disp
517,3 493,4
[KN]
Momento Máx
60,1
56,9
[KN-m/m]
Fuerza Corte Máx
80,9
77,1
[KN/m]
Fuerza Normal
155,4 152,7
Máx [KN/m]
Desp. Máx [mm]
10,1
9,2
Espesor ademes
7,1
6,9
[cm]
Prof. Enterramiento
3,36
3,24
[m]
St
St
St
St
St
St
St
St
1570/1 1080/1 1080/1 1080/1 1080/1 1080/1 1080/1 835/10
770 3
230
230
230
230
230
230
30
litzen diámetro diámetro diámetro diámetro diámetro diámetro diámetro
26,5
26,5
26,5
26,5
26,5
26,5
26,5
0,6''
348,7
334,2
320,5
307,2
294,4
282
269,8
258,2
9,9
9,52
9,04
8,59
8,27
7,86
7,47
7,19
147
140,4
133,9
127,6
121,6
115,8
110,5
105,1
St
St
St
St
St
St
St
St
835/10 835/10 835/10 835/10 835/10 1570/1 1570/1 1080/1
770 3 770 3
30
30
30
30
30
230
diámetro diámetro diámetro diámetro diámetro litzen
litzen diámetro
36
36
36
36
36
26,5
0,6''
0,6''
470,6
449,6
428,6
408,5
389,2
370,7
353,6
336,6
53,9
51,3
48,5
45,9
43,5
41,1
39,1
37
73,4
70
66,6
63,3
60,2
57,2
54,5
51,8
150,1
146,7
144
141,2
138,3
135,5
132,1
129,2
8,5
11,7
10,7
9,8
9
8,2
11,7
10,8
6,8
6,6
6,5
6,3
6,2
6,1
5,9
5,8
3,12
3
2,88
2,76
2,64
2,52
2,52
2,4
ANEXO 14 Tabla de salida para =10° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 1,6 m. Caso 3.
100
Separación entre perfiles 2,5 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 5 [m]
Ángulo de anclaje
Ѳ=20[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
240
240
240
240
220
220
220
220
200
200
11,36
10,92
10,62
10,21
9,82
9,45
9,09
8,85
8,52
8,19
123,5
118,5
113,7
109,1
104,6
100,2
96,11
92,07
88,11
84,34
St
St
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 835/10 835/10 835/10
Acero seleccionado 770 5 770 5 770 5 770 5 770 5 770 4
30
30
30
litzen litzen litzen litzen litzen litzen diámetro diámetro diámetro
36
36
36
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
617,6 592,8 568,9 545,7
523
501,4 480,5 460,4 440,6
[KN]
Longitud anclaje
9,74
9,29
8,96
8,55
8,16
7,79
7,43
7,19
6,87
[m]
Fuerza Normal
171,3 163,3 155,7 148,5 141,7 135,1 128,6 122,5 116,8
[KN/m]
St
St
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1
Acero seleccionado 770 7 770 7 770 7 770 6 770 6 770 6 770 6 770 5 770 5
litzen litzen litzen litzen litzen litzen litzen litzen litzen
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
856,5 816,9 778,9 742,5 708,9 675,5 643,4 612,7 584,3
[KN]
Momento Máx
61,9
58,5
55,4
52,4
49,8
47,1
44,5
42,1
40
[KN-m/m]
Fuerza Corte Máx
82,2
78,3
74,5
70,9
67,6
64,3
61,1
58
55,3
[KN/m]
Fuerza Normal
207,1 202,2 197,3 192,4 187,2 182,5 177,8 173,1 168,1
Máx [KN/m]
Desp. Máx [mm]
9,2
8,4
7,7
7,1
9,1
8,3
7,6
7
9,1
Espesor ademes
11
10,8
10,6
10,3
10,1
9,9
9,7
9,5
9,3
[cm]
Prof. Enterramiento
3,72
3,6
3,48
3,36
3,24
3,12
3
2,88
2,76
[m]
St
835/10
30
diámetro
36
421,7
6,56
111,2
St
1570/1
770 5
litzen
0,6''
556
37,8
52,5
163,6
8,3
9,1
2,64
ANEXO 15 Tabla de salida para =20° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2,5 m. Caso 3.
101
Separación entre perfiles 2 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 4 [m]
Ángulo de anclaje
Ѳ=20[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
220
220
220
220
200
200
200
200
200
180
11,23
10,79
10,37
10,09
9,7
9,33
8,98
8,74
8,41
8,19
123,7
118,8
114
109,3
104,8
100,4
96,28
92,22
88,3
84,47
St
St
St
St
St
St
St
St
1080/1 835/10 835/10 835/10 835/10 835/10 835/10 1570/1
Acero seleccionado 230
770 3
30
30
30
30
30
30
diámetro diámetro diámetro diámetro diámetro diámetro diámetro litzen
32
36
36
36
36
36
36
0,6''
Carga anclaje disp
495,2 475,3
456
437,5 419,2 401,9 385,1 368,9
[KN]
Longitud anclaje
9,62
9,17
8,74
8,44
8,05
7,68
7,33
7,09
[m]
Fuerza Normal
170,2 162,4 154,8 147,6
141
134,3
128
121,9
[KN/m]
St
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1080/1
Acero seleccionado 770 6 770 6 770 5 770 5 770 5 770 5 770 5
230
litzen litzen litzen litzen litzen litzen litzen diámetro
32
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
681,2 649,7 619,6 590,7 564,1 537,5 512,1 487,7
[KN]
Momento Máx
60,9
57,6
54,5
51,6
49,1
46,4
43,9
41,5
[KN-m/m]
Fuerza Corte Máx
81,6
77,6
73,9
70,3
67,1
63,8
60,6
57,6
[KN/m]
Fuerza Normal
207,1 202,2 197,3 192,5 187,3 182,5 177,8 173,2
Máx [KN/m]
Desp. Máx [mm]
9,6
8,8
8,1
7,4
9,7
8,9
8,1
7,4
Espesor ademes
8,8
8,6
8,5
8,3
8,1
7,9
7,7
7,6
[cm]
Prof. Enterramiento
3,6
3,36
3,24
3,12
3
2,88
2,76
2,64
[m]
St
St
1570/1 1080/1
770 3
230
litzen diámetro
26,5
0,6''
353,2
337,9
6,77
6,55
116,1
110,6
St
St
835/10 835/10
30
30
diámetro diámetro
36
36
464,4
442,7
39,3
37,3
54,8
52,1
168,1
163,5
10,1
9,3
7,4
7,2
2,52
2,52
ANEXO 16 Tabla de salida para =20° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2 m. Caso 3.
102
Separación entre perfiles 1,6 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 3,2 [m]
Ángulo de anclaje
Ѳ=20[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
200
200
200
200
180
180
180
180
180
160
11,1
10,66
10,25
9,97
9,59
9,22
8,98
8,63
8,3
8,09
124
119
114,2
109,5
104,9
100,6
96,43
92,36
88,43
84,58
St
St
St
835/10 835/10 1570/1
Acero seleccionado
770 3
30
30
diámetro diámetro litzen
36
32
0,6''
Carga anclaje disp
397
381
365,5
[KN]
Longitud anclaje
9,5
9,05
8,62
[m]
Fuerza Normal
169,3 161,5
154
[KN/m]
St
St
St
1570/1 1570/1 1080/1
Acero seleccionado 770 5 770 5
230
litzen litzen diámetro
36
0,6''
0,6''
Carga anclaje disp
541,8 516,9 492,9
[KN]
Momento Máx
60
56,8
53,8
[KN-m/m]
Fuerza Corte Máx
80,9
77
73,3
[KN/m]
Fuerza Normal
207,1 202,2 197,3
Máx [KN/m]
Desp. Máx [mm]
10,2
9,4
8,6
Espesor ademes
7,1
6,9
6,8
[cm]
Prof. Enterramiento
3,36
3,24
3,12
[m]
St
St
St
St
St
St
St
1570/1 1080/1 1080/1 1080/1 1080/1 1080/1 1080/1
770 3
230
230
230
230
230
230
litzen diámetro diámetro diámetro diámetro diámetro diámetro
26,5
26,5
26,5
26,5
26,5
26,5
0,6''
350,6
336
322
308,6
295,6
283
270,7
8,32
7,94
7,57
7,32
6,99
6,67
6,46
146,8
140,3
133,7
127,4
121,3
115,5
110,1
St
St
St
St
St
St
St
835/10 835/10 835/10 835/10 835/10 1570/1 1570/1
770 3 770 3
30
30
30
30
30
diámetro diámetro diámetro diámetro diámetro litzen
litzen
36
36
36
36
36
0,6''
0,6''
470
448,9
427,9
407,7
388,3
369,8
352,6
50,9
48,4
45,8
43,4
41
38,8
36,9
69,8
66,5
63,3
60,2
57,2
54,4
51,8
192,5
187,2
182,5
177,8
173,2
168,6
163,5
7,9
10,9
10
9,1
8,4
7,7
10,9
6,6
6,5
6,3
6,2
6,1
5,9
5,8
3
2,88
2,76
2,64
2,52
2,4
2,4
ANEXO 17 Tabla de salida para =20° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 1,6 m. Caso 3.
103
Separación entre perfiles 2,5 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 5 [m]
Ángulo de anclaje
Ѳ=30[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
260
240
240
240
240
220
220
220
220
200
10,37
10
9,76
9,42
9,09
8,77
8,46
8,27
7,98
7,7
134,2
128,7
123,5
118,5
113,6
108,8
104,3
99,97
95,73
91,56
St
St
St
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 835/10 835/10
Acero seleccionado 770 6 770 6 770 5 770 5 770 5 770 5 770 5 770 4
30
30
litzen litzen litzen litzen litzen litzen litzen litzen diámetro diámetro
36
36
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
671,1 643,7 617,7 592,6 568,3 544,4 521,7 499,8 478,6 457,8
[KN]
Longitud anclaje
10,38
8,47
8,2
7,85
7,52
7,2
6,89
6,69
6,41
6,14
[m]
Fuerza Normal
185,3
177
168,8 160,9 153,3 146,4 139,4 132,7 126,4 120,5
[KN/m]
St
St
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 1570/1
No
Acero seleccionado
770 7 770 7 770 7 770 7 770 6 770 6 770 6 770 6 770 5
aplica
litzen litzen litzen litzen litzen litzen litzen litzen litzen
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
926.5 885,2 844,1 804,6 766,8 732,1 697,3
664
632
602,6
[KN]
Momento Máx
61,2
58,2
55,1
52,1
49,3
46,9
44,3
41,9
39,6
37,6
[KN-m/m]
Fuerza Corte Máx
81,9
78,2
74,4
70,8
67,3
64,2
61
58
55,1
52,4
[KN/m]
Fuerza Normal
266,4 258,6 251,3
244
237
229,6 222,8 216,1 209,5 202,7
Máx [KN/m]
Desp. Máx [mm]
7,2
8,7
8
7,3
6,7
8,6
7,9
7,2
6,7
8,6
Espesor ademes
11
10,8
10,6
10,3
10,1
9,9
9,7
9,5
9,3
9,1
[cm]
Prof. Enterramiento
3,72
3,6
3,48
3,36
3,24
3,12
3
2,88
2,76
2,64
[m]
ANEXO 18 Tabla de salida para =30° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2,5 m. Caso 3.
104
Separación entre perfiles 2 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 4 [m]
Ángulo de anclaje
Ѳ=30[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
220
220
220
220
200
200
200
200
200
180
10,25
9,89
9,53
9,31
8,98
8,66
8,36
8,17
7,88
7,7
134,4
129
123,7
118,7
113,7
109
104,5
100,1
95,87
91,69
St
St
St
1570/1 1570/1 1080/1
Acero seleccionado 770 5 770 5
230
litzen litzen diámetro
32
0,6''
0,6''
Carga anclaje disp
537,6
516
495,2
[KN]
Longitud anclaje
8,75
9,9
8
[m]
Fuerza Normal
184,58 176,04 167,86
[KN/m]
St
St
St
1570/1 1570/1 1570/1
Acero seleccionado 770 6 770 6 770 6
litzen litzen litzen
0,6''
0,6''
0,6''
Carga anclaje disp
738,3 704,1 671,4
[KN]
Momento Máx
60,7
57,4
54,3
[KN-m/m]
Fuerza Corte Máx
81,5
77,5
73,8
[KN/m]
Fuerza Normal
266
285,5 251,2
Máx [KN/m]
Desp. Máx [mm]
9,9
9,1
8,3
Espesor ademes
8,8
8,6
8,5
[cm]
Prof. Enterramiento
3,6
3,36
3,24
[m]
St
St
St
St
St
St
St
835/10 835/10 835/10 835/10 835/10 835/10 1570/1
770 3
30
30
30
30
30
30
diámetro diámetro diámetro diámetro diámetro diámetro litzen
36
36
36
36
36
32
0,6''
474,9
455,1
436,3
418,1
400,5
383,5
366,8
7,75
7,42
7,1
6,8
6,6
6,32
6,14
160,05 152,86 145,66 138,76 132,15 125,81 119,97
St
St
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 1570/1 1570/1 835/10
770 6 770 5 770 5 770 5 770 5 770 5
30
litzen litzen litzen litzen litzen litzen diámetro
36
0,6''
0,6''
0,6''
0,6''
0,6''
0,6''
640,2
611,4
582,6
555
528,6
503,2
479,9
51,4
48,9
46,3
43,7
41,4
39,1
37,2
70,2
67
63,7
60,5
57,5
54,7
52,1
244
236,5
229,6
222,8
216,1
209,5
202,6
7,6
9,9
9,1
8,3
7,6
7,2
9,8
8,3
8,1
7,9
7,7
7,6
7,4
7,2
3,12
3
2,88
2,76
2,64
2,52
2,52
ANEXO 19 Tabla de salida para =30° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 2 m. Caso 3.
105
Separación entre perfiles 1,6 [m]
Anclaje Inferior
Anclaje Superior
Separación entre anclajes de 3,2 [m]
Ángulo de anclaje
Ѳ=30[°]
φ=28°
φ=29°
φ=30°
φ=31°
φ=32°
φ=33°
φ=34°
φ=35°
φ=36°
φ=37°
Perfil HEB
Longitud anclaje
[m]
Fuerza Normal
[KN/m]
200
200
200
200
200
180
180
180
180
180
10,14
9,77
9,42
9,2
8,87
8,56
8,36
8,07
7,78
7,61
134,6
129,2
124
118,9
114
109,2
104,6
100,2
96
91,87
St
St
St
St
St
835/10 835/10 835/10 835/10 1570/1
Acero seleccionado
770 3
30
30
30
30
diámetro diámetro diámetro diámetro litzen
36
36
36
32
0,6''
Carga anclaje disp
430,9 413,6 396,8 380,6
365
[KN]
Longitud anclaje
10,15
8,26
7,9
7,65
7,32
[m]
Fuerza Normal
183,5
175
166,9 159,2 151,7
[KN/m]
St
St
St
St
St
1570/1 1570/1 1570/1 1570/1 835/10
Acero seleccionado 770 5 770 5 770 5 770 5
30
litzen litzen litzen litzen diámetro
32
0,6''
0,6''
0,6''
0,6''
Carga anclaje disp
587,4 560,3 534,4 509,5 485,7
[KN]
Momento Máx
59,8
56,6
53,6
50,7
48
[KN-m/m]
Fuerza Corte Máx
80,8
76,9
73,2
69,7
66,3
[KN/m]
Fuerza Normal
265,9 258,4 251,1 243,9 236,9
Máx [KN/m]
Desp. Máx [mm]
10,5
9,6
8,8
8,1
11,1
Espesor ademes
7,1
6,9
6,8
6,6
6,5
[cm]
Prof. Enterramiento
3,36
3,24
3,12
3
2,88
[m]
St
St
St
St
St
1570/1 1080/1 1080/1 1080/1 1080/1
770 3
230
230
230
230
litzen diámetro diámetro diámetro diámetro
26,5
26,5
26,5
26,5
0,6''
349,6
335
320,8
307,2
294
7,01
6,8
6,51
6,23
6,05
144,9
138,1
131,5
125,2
119,2
St
St
St
St
St
835/10 835/10 835/10 835/10 835/10
30
30
30
30
30
diámetro diámetro diámetro diámetro diámetro
36
36
36
36
32
463,9
442
421
400,8
381,5
45,7
43,2
40,9
38,7
36,6
63,2
60,1
57,1
54,3
51,7
229,4
222,6
216
209,4
203
10,2
9,3
8,6
8,1
7,6
6,3
6,2
6,1
5,9
5,8
2,76
2,64
2,52
2,4
2,28
ANEXO 20 Tabla de salida para =30° (ángulo de inclinación para ambos anclajes) y separación entre perfiles
de 1,6 m. Caso 3.
106
φ[°]
28
29
30
31
32
33
34
35
36
37
θ[°]
240
240
240
240
220
220
220
220
200
200
10°
Sep. entre
perfiles
[m]
240
240
240
240
220
220
220
220
200
200
20°
260
240
240
240
240
220
220
220
220
200
30°
PERFILES DE ACERO HEB
220
220
220
220
220
220
220
220
220
200
220
220
200
200
200
200
200
200
200
200
200
200
200
200
180
200
200
180
180
180
10°
20°
30°
2,5 m
200
200
200
180
180
180
180
180
160
160
10°
200
200
200
200
180
180
180
180
180
160
20°
2m
1,6 m
3,72
3,6
3,48
3,36
3,24
3,12
3
2,88
2,76
2,64
20°
LONGITUD DE ENTERRAMIENTO [m]
3,72
3,6
3,6
3,6
3,36
3,6
3,36
3,36
3,36
3,24
3,48
3,24
3,24
3,24
3,12
3,36
3,12
3,12
3,12
3
3,24
3
3
3
2,88
3,12
2,88
2,88
2,88
2,76
3
2,76
2,76
2,76
2,64
2,88
2,64
2,64
2,64
2,52
2,76
2,64
2,52
2,52
2,52
2,64
2,52
2,52
2,52
2,4
30°
10°
20°
30°
10°
3,36
3,24
3,12
3
2,88
2,76
2,64
2,52
2,4
2,28
20°
2,5 m
2m
1,6 m
200
200
200
200
200
180
180
180
180
180
30°
ANEXO 21 Perfiles de acero HEB óptimos para caso 3.
φ[°]
28
29
30
31
32
33
34
35
36
37
θ[°]
Sep. entre
perfiles
[m]
3,72
3,6
3,48
3,36
3,24
3,12
3
2,76
2,76
2,64
10°
3,36
3,24
3,12
3
2,88
2,76
2,64
2,52
2,4
2,28
30°
ANEXO 22 Longitud de enterramiento del perfil de acero (m) para caso 3.
107
φ[°]
28
29
30
31
32
33
34
35
36
37
FUERZA NORMAL ANCLAJES SUPERIOR E INFERIOR [KN/m]
117,8
163,5
123,5
171,3
134,2
185
118
162,5
123,7
170,2
134,4
184,5
118,3
161,6
124
169,3
134,6
183,5
113
156
118,5
163,3
128,7
177
113,3
155
118,8
162,4
129
176
113,5
154,2
119
161,5
129,2
175
108,5
148,7
113,7
155,7
123,5
168,8
108,7
147,8
114
154,8
123,7
167,8
108,9
147
114,2
154
124
166,9
104
142
109,1
148,5
118,5
160,9
104,2
141,2
109,3
147,6
118,7
160
104,4
140,4
109,5
146,8
118,9
159,2
99,77
135,3
104,6
141,7
113,6
153,3
99,97
134,6
104,8
141
113,7
152,8
100,1
133,9
104,9
140,3
114
151,7
95,66
129
100,2
135,1
108,8
146,4
95,84
128,3
100,4
134,3
109
145,6
96
127,6
100,6
133,7
109,2
144,9
91,67
122,8
96,11
128,6
104,3
139,4
91,84
122,2
96,28
128
104,5
138,7
91,99
121,6
96,43
127,4
104,6
138,1
87,82
117
92,07
122,5
99,97
132,7
87,97
116,4
92,22
121,9
100,1
132,1
88,11
115,8
92,36
121,3
100,2
131,5
84,05
111,5
88,11
116,8
95,73
126,4
84,19
111
88,3
116,1
95,87
125,8
84,31
110,5
88,43
115,5
96
125,2
80,45
106,1
84,34
111,2
91,56
120,5
80,58
105,6
84,47
110,6
91,69
119,9
80,69
105,1
84,58
110,1
91,87
119,2
10° sup 10° inf 20° sup 20° inf 30° sup 30° inf 10° sup 10° inf 20° sup 20° inf 30° sup 30° inf 10° sup 10° inf 20° sup 20° inf 30° sup 30° inf
2,5 m
2m
1,6 m
Sep. [m ]
θ[°]
ANEXO 23 Fuerza Normal para anclajes superior e inferior para caso 3.
φ[°]
28
29
30
31
32
33
34
35
36
37
LONGITUD ANCLAJES SUPERIORES E INFERIORES [m]
15,9
9,7
11,3
9,74
10,3
10,3
15,8
9,54
11,2
9,62
10,2
8,75
12,7
11
11,1
9,5
10,1
10,1
12,4
10,7
10,9
12
10,3
10,6
9,29
10
8,47
12,3
10,5
10,7
9,17
9,89
9,9
12,1
10,4
10,6
9,05
9,77
8,26
8,96
9,76
8,2
11,8
10
10,3
8,74
9,53
8
11,6
9,9
10,2
8,62
9,42
7,9
11,5
9,78
10,2
8,55
9,42
7,85
11,4
9,65
10
8,44
9,31
7,75
11,3
9,52
9,97
8,32
9,2
7,65
11
9,3
9,82
8,16
9,09
7,52
10,9
9,17
9,7
8,05
8,98
7,42
10,8
9,04
9,59
7,94
8,87
7,32
10,6
8,83
9,45
7,79
8,77
7,2
10,4
8,71
9,33
7,68
8,66
7,1
10,3
8,59
9,22
7,57
8,56
7,01
10,1
8,39
9,09
7,43
8,46
6,89
10
8,27
8,98
7,33
8,36
6,8
10
8,27
8,98
7,32
8,36
6,8
10,1
8,39
8,85
7,19
8,27
6,69
9,75
7,97
8,74
7,09
8,17
6,6
9,63
7,86
8,63
6,99
8,07
6,51
9,46
7,69
8,52
6,87
7,98
6,41
9,34
7,58
8,41
6,77
7,88
6,32
9,22
7,47
8,3
6,67
7,78
6,23
9,07
7,31
8,19
6,56
7,7
6,14
9,07
7,3
8,19
6,55
7,7
6,14
8,95
7,19
8,09
6,46
7,61
6,05
10° sup 10° inf 20° sup 20° inf 30° sup 30° inf 10° sup 10° inf 20° sup 20° inf 30° sup 30° inf 10° sup 10° inf 20° sup 20° inf 30° sup 30° inf
2,5 m
2m
1,6 m
Sep. [m ]
θ[°]
ANEXO 24 Longitud de anclajes (m) para caso 3.
108
φ[°]
28
29
30
31
32
33
34
35
36
37
θ[°]
11
10,8
10,6
10,3
10,1
9,9
9,7
9,5
9,3
9,1
10°
11
10,8
10,6
10,3
10,1
9,9
9,7
9,5
9,3
9,1
20°
Sep. entre
perfiles
[m]
11
10,8
10,6
10,3
10,1
9,9
9,7
9,5
9,3
9,1
30°
ESPESOR DE ADEMES [cm]
8,8
8,8
8,8
8,6
8,6
8,6
8,5
8,5
8,5
8,3
8,3
8,3
8,1
8,1
8,1
7,9
7,9
7,9
7,7
7,7
7,7
7,6
7,6
7,6
7,4
7,4
7,4
7,2
7,2
7,2
10°
20°
30°
2,5 m
2m
7,1
6,9
6,8
6,6
6,5
6,3
6,2
6,1
5,9
5,8
10°
7,1
6,9
6,8
6,6
6,5
6,3
6,2
6,1
5,9
5,8
20°
7,1
6,9
6,8
6,6
6,5
6,3
6,2
6,1
5,9
5,8
30°
1,6 m
ANEXO 25 Espesor de ademes de madera (cm) para caso 3.
φ[°]
28
29
30
31
32
33
34
35
36
37
θ[°]
Sep. entre
perfiles
[m]
9
8,3
7,6
7
8,9
8,2
7,5
6,8
8,9
8,2
10°
9,2
8,4
7,7
7,1
9,1
8,3
7,6
7
9,1
8,3
20°
2,5 m
DESPLAZAMIENTO HORIZONTAL MAXIMO [mm]
7,2
9,4
9,6
9,9
10,1
10,2
8,7
8,6
8,8
9,1
9,2
9,4
8
7,9
8,1
8,3
8,5
8,6
7,3
10,4
7,4
7,6
11,7
7,9
6,7
9,5
9,7
9,9
10,7
10,9
8,6
8,7
8,9
9,1
9,8
10
7,9
8
8,1
8,3
9
9,1
7,2
7,3
7,4
7,6
8,2
8,4
6,7
10,1
10,1
7,2
11,7
7,7
8,6
9,2
9,3
9,8
10,8
10,9
30°
10°
20°
30°
10°
20°
2m
10,5
9,6
8,8
8,1
11,1
10,2
9,3
8,6
8,1
7,6
30°
1,6 m
ANEXO 26 Desplazamiento horizontal máximo del muro (mm) para caso 3.
109
7. Salidas del programa
110
ANEXO 27 Salida del programa GGU-RETAIN para Caso 2, con una separación de 1,6 m y θ=10°.
ANEXO 28 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2 m y θ=10°.
111
ANEXO 29 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2,5 m y θ=10°.
ANEXO 30 Salida del programa GGU-RETAIN para Caso 2, con una separación de 1,6 m y θ=20°.
112
ANEXO 31 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2 m y θ=20°.
ANEXO 32 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2,5 m y θ=20°.
113
ANEXO 33 Salida del programa GGU-RETAIN para Caso 2, con una separación de 1,6 m y θ=30°.
ANEXO 34 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2 m y θ=30°.
114
ANEXO 35 Salida del programa GGU-RETAIN para Caso 2, con una separación de 2,5 m y θ=30°.
115