modelado de las características de embalses y centrales
Anuncio

UNIVERSIDAD PONTIFICIA COMILLAS
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA (ICAI)
INGENIERO INDUSTRIAL
PROYECTO FIN DE CARRERA
MODELADO DE LAS
CARACTERÍSTICAS DE EMBALSES Y
CENTRALES HIDROELÉCTRICAS
AUTOR:
JUAN PALOMARES CARRALERO
MADRID, JUNIO DE 2008
Autorizada la entrega del proyecto al alumno:
Juan Palomares Carralero
LOS DIRECTORES DEL PROYECTO
Rafael Bellido Miranda
Fdo:
Fecha:
Alejandro Perea Sánchez
Fdo:
Fecha:
Vº Bº del Coordinador de Proyectos
Tomás Gómez San Román
Fdo:
Fecha:
iii
Resumen
Este proyecto surge como una necesidad de desarrollo de una aplicación que
modele las características de embalses y centrales hidroeléctricas, sirviendo como
herramienta para la optimización y gestión de recursos hidroeléctricos que lleva a cabo
el departamento de Planificación y Ofertas (PYOFE) de Iberdrola.
PYOFE es una unidad que se encuentra dentro del organigrama general de la
empresa bajo la dirección de Gestión de la Energía en el área de Negocio Liberalizado.
Las funciones que PYOFE tiene a su cargo son muy diversas: la planificación de la
producción de las plantas de generación, la realización de ofertas al mercado, la
estimación de la evolución del mercado, etc. La optimización y gestión de recursos
hidroeléctricos desempeña un papel fundamental dentro de estas funciones, debido a
la dificultad que entraña la gestión de las centrales hidroeléctricas a causa de la
incertidumbre de las aportaciones.
Hasta el momento Iberdrola hacía uso del programa llamado Modelo Hidráulico
(MODHI) como herramienta fundamental de almacenamiento y cálculo de
características de embalses y centrales hidroeléctricas. Este programa constituye, junto
con otras herramientas, la base en la que se apoya la optimización y la gestión del agua.
El MODHI funciona en una versión del sistema operativo VMS. El acceso al mismo es
únicamente a través de un emulador de una consola de VAX - VMS, y la extracción de
datos así como el manejo de las funciones que contiene se tiene que hacer
fundamentalmente mediante programación en el lenguaje Fortran o por pantalla.
El sistema operativo VMS y la programación en Fortran eran ventajosos en tanto en
cuanto a que la velocidad de cálculo es casi instantánea, se cuida al extremo detalles
como la capacidad de memoria o la longitud de las variables, y la forma de organizar
los datos y estructurar los códigos es rigurosa y óptima. Sin embargo, hoy en día puede
resultar tedioso el manejo de un programa en este entorno, puesto que en la mayoría
de las empresas la optimización y la planificación se realizan en entornos de Excel y
Matlab, usando lenguajes de programación como Visual Basic for Applications.
Por tanto, el proyecto consiste en la elaboración de una herramienta en Excel
llamada Características Hidroeléctricas (CARHI) que sustituya al MODHI. No sólo lo
iv
sustituya en el sentido estricto de la palabra, sino que también lo mejore y lo amplíe. El
CARHI es una aplicación que se desarrolla en Excel para que los datos y resultados que
proporciona sean más fácilmente exportables a programas de planificación y
optimización que también están desarrollados en Excel. Asimismo, la herramienta
CARHI se apoya en programación en Visual Basic for Applications (VBA), que permite
tanto el manejo y cálculo de funciones a partir de las variables que caracterizan a los
embalses y centrales de Iberdrola como el desarrollo de interfaces en Excel que faciliten
el trabajo a los usuarios de la herramienta.
Cabe mencionar que el proyecto de creación del CARHI implica a su vez la
programación en Fortran, necesaria para extraer toda la información que proporciona
el MODHI. También requiere del manejo y control de datos tanto analítica como
gráficamente en Matlab, para examinar que toda la información obtenida es correcta,
detectando y filtrando posibles errores que pudiera haber en la extracción de datos del
MODHI o que simplemente fueran consecuencia de ruido introducido al programar en
Fortran. Otra implicación adicional es el conocimiento de conceptos hidráulicos y de la
física de los fluidos, centrándose concretamente en todo el estudio de los embalses y las
centrales. Este conocimiento es necesario para entender las variables que se manejan y
para saber en todo momento si los resultados obtenidos tienen sentido real o no. Por
último, el proyecto conlleva conocimientos puramente matemáticos para la correcta
realización de cálculos, iteraciones y ajustes de curvas.
Aparte de la mejora operativa y gráfica que supone pasar a tener la herramienta en
Excel, este proyecto ha supuesto una ampliación respecto de lo que proporcionaba el
MODHI: incorpora información general de las cuencas hidráulicas, muestra
información gráfica de las funciones, ofrece topología de los sistemas hidráulicos,
ajusta funciones inversas que no existían explícitamente en el MODHI como es la curva
volumen de embalse - cota de embalse, proporciona curvas y colinas de rendimiento
de las turbinas, y añade más características como son los coeficientes energéticos a
plena carga y de máximo rendimiento.
En definitiva, se trata de un proyecto amplio que abarca temas diversos: desde la
programación en diferentes lenguajes, al estudio hidrodinámico y su aplicación en los
embalses y centrales hidroeléctricas, pasando por la optimización del tiempo de
proceso mediante iteraciones que agilicen el cálculo de características hidroeléctricas, y
el desarrollo de interfaces que faciliten al usuario el manejo de la aplicación CARHI.
v
Summary
This project arose from a need of development of an application that models the
characteristics of reservoirs and hydraulic plants. This application is used as a tool for
optimization and management of hydroelectric resources, both of which are tasks of
the department of Planificación y Ofertas (PYOFE) of Iberdrola.
PYOFE is a department of Gestión de la Energía, which is a section under Negocio
Liberalizado on the hierarchical chain of command of Iberdrola. The functions that
PYOFE executes are very diverse: planning of electricity production, realizing market
offers, estimation of market evolution, etc.
All of these functions rely partly on
hydroelectricity. Besides, there is a great difficulty in managing hydroelectric plants
due to the uncertainty of water contributions. Thus, the optimization and management
of hydroelectric resources is specifically important in order to carry out all of these
functions in the best way possible.
Until now, Iberdrola has been using a program called Modelo Hidráulico (MODHI)
as a fundamental tool of data storage and calculation of characteristics of reservoirs
and hydraulic plants.
This program, along with other tools, is used for the
optimization and management of water. MODHI functions with a version of the VMS
operating system. Access to the VMS operating system is only carried out by simulator
of the VAX – VMS console. The extraction of its data, as well as the programming that
lies behind the application, has to be done by means of Fortran programming language
or manually.
The VMS operating system and programming in Fortran language suppose an
advantage in processing information quickly, since details such as the memory
capacity or the length of the variables allow for smooth operation.
Moreover, the
structure of the codes and the way in which the data is organized are strict and
optimum. Nevertheless, nowadays the management of a program in this environment
can be tedious, since the majority of businesses carry out optimization and planning by
utilizing Excel and Matlab, with programming languages such as Visual Basic for
Applications.
Therefore, the project consists of the elaboration in Excel of a tool called
Características Hidroeléctricas (CARHI), which replaces the MODHI software. It not
vi
only substitutes, in the strict sense of the word, but also improves and expands upon
the program. CARHI is supported by the program Excel, so that the data and results
that it provides are exportable to other programs for planning and optimization that
are also developed in Excel. CARHI does not only rely on Excel, but also on Visual
Basic language, which permits the calculation of characteristics of reservoirs and
hydroelectric plants of Iberdrola. Visual Basic also allows the existence of interfaces
throughout the CARHI application, which facilitate the work to the users of the tool.
It is important to mention that the first step in the creation of CARHI implied
programming in Fortran, in order to extract all the information that MODHI contains.
The next step was to control and manage all data analytically and graphically in
Matlab, in order to check that all of the information extracted is correct, detecting and
filtering errors that could have been yielded during the extraction of the data. An
additional implication of this project is the knowledge of hydraulic concepts and of the
physics of fluids, particularly concepts related to the study of reservoirs and
hydroelectric plants. This knowledge is necessary to understand the variables that are
managed and to know whether or not the results obtained are correct. Finally, the
project involves mathematical knowledge necessary for the calculation, iteration and
adjustment of curves.
Aside from the graphic and operating improvement that CARHI entails, there are
many new functions: it incorporates general information of hydraulic basins, displays
graphic information of the functions, allows access to topology of the hydraulic
systems, adjusts inverse functions that did not exist explicitly in MODHI, such as
volume – height curve, provides efficiency curves and hills of the turbines, and adds
more characteristics, such as energy coefficients.
It is an extensive project that covers diverse themes; from programming in different
languages and studying water physics and its application on reservoirs and hydraulic
plants, to realizing iterations that improve the calculations of hydraulic characteristics
and developing interfaces that help the user to work with CARHI.
vii
Índice
RESUMEN ...............................................................................................................................................III
SUMMARY .............................................................................................................................................. V
ÍNDICE................................................................................................................................................... VII
ÍNDICE DE FIGURAS ........................................................................................................................ XII
ÍNDICE DE ECUACIONES .............................................................................................................. XIV
ÍNDICE DE TABLAS............................................................................................................................XV
1 INTRODUCCIÓN.............................................................................................................................. 2
1.1 Motivación........................................................................................................... 2
1.2 Descripción del problema ................................................................................. 3
1.3 Objetivos y estructura del proyecto................................................................. 4
1.3.1
Estudio de conceptos hidráulicos y de aspectos relacionados con la gestión de
recursos hidroeléctricos
1.3.2
5
Programa MODHI: extracción y control de datos mediante programación en
Fortran y en Visual Basic for Applications
5
1.3.3
Tratamiento analítico y gráfico de características hidroeléctricas en Matlab
6
1.3.4
Diseño y modelado de la herramienta CARHI
6
2 CONCEPTOS HIDRÁULICOS........................................................................................................ 8
2.1 Introducción ........................................................................................................ 8
2.2 Definiciones......................................................................................................... 8
2.3 Ecuaciones básicas.............................................................................................. 9
2.3.1
Ley de continuidad
9
2.3.2
Principio fundamental de la hidrostática
9
2.3.3
Teorema de Torricelli
11
2.3.4
Teorema de Bernouilli
12
2.4 Características de los embalses....................................................................... 13
2.4.1
Introducción
13
2.4.2
Tipos
14
2.4.3
Cota
15
2.4.4
Curvas de resguardo
15
2.4.5
Curva de garantía (o de hierro)
16
2.4.6
Volúmenes
16
2.4.7
Desagües
17
viii
2.5 Características de las centrales hidroeléctricas ............................................ 18
2.5.1
Introducción
18
2.5.2
Tipos
19
2.5.3
Saltos
20
2.5.4
Caudal y aportación
21
2.5.5
Potencia
22
2.5.6
Rendimiento
23
2.5.7
Coeficiente energético y producible hidráulico
25
2.5.8
Conducciones de agua
26
2.5.9
Turbinas
28
3 MARCO RETRIBUTIVO DE LA PRODUCCIÓN HIDROELÉCTRICA............................... 31
3.1 Introducción ...................................................................................................... 31
3.2 Ley del Sector Eléctrico (Ley 54/1997) .......................................................... 31
3.2.1
Introducción y antecedentes
31
3.2.2
Objetivos
31
3.2.3
Mercado eléctrico
33
3.2.4
Ley 17/2007
34
3.3 Producción hidroeléctrica ............................................................................... 34
3.4 Marco retributivo del régimen ordinario...................................................... 34
3.5 Conclusiones ..................................................................................................... 35
4 SISTEMAS HIDROELÉCTRICOS GESTIONADOS POR IBERDROLA............................. 37
4.1 Introducción ...................................................................................................... 37
4.2 Restricciones...................................................................................................... 37
4.3 Gestión de la energía........................................................................................ 38
4.4 Sistemas de generación.................................................................................... 39
4.5 Optimización y gestión de sistemas hidroeléctricos ................................... 40
4.6 Características de los sistemas hidroeléctricos de Iberdrola...................... 42
4.6.1
Introducción
42
4.6.2
Sil
43
4.6.3
Duero
43
4.6.4
Tajo
44
4.6.5
Sistemas del Ebro y Levante
47
4.7 Conclusión......................................................................................................... 48
5 MODELADO DE LAS CARACTERÍSTICAS HIDROELÉCTRICAS .................................... 50
5.1 Introducción ...................................................................................................... 50
ix
5.2 Modelo Hidráulico (MODHI)......................................................................... 51
5.2.1
Introducción
51
5.2.2
Descripción
51
5.2.3
Extracción de datos con Fortran
53
5.2.4
Control de datos en Excel con VBA
57
5.3 Características hidroeléctricas (CARHI) ....................................................... 60
5.3.1
Introducción
60
5.3.2
Tratamiento de datos en Matlab
60
5.3.2.1
Volumen útil y volumen total en función de la cota del embalse..................................... 62
5.3.2.2
Cota de desagüe en función del caudal turbinado y vertido total de la central, la
cota del embalse aguas abajo y el caudal turbinado por la central paralela ...................................... 64
5.3.2.3
Pérdida de carga en función del caudal turbinado por un grupo y del número
de grupos turbinando ............................................................................................................................... 67
5.3.2.4
Caudal unitario en función de la potencia de generación unitaria y potencia de
generación unitaria en función del caudal unitario, para distintos saltos netos ............................... 69
5.3.2.5
Potencia unitaria máxima y caudal unitario máximo en función del salto neto............. 71
5.3.2.6
Potencia de bombeo y caudal de bombeo en función del salto bruto y del
número de grupos ..................................................................................................................................... 73
5.3.3
5.3.4
Desarrollo de la herramienta CARHI
74
5.3.3.1
Organización de la herramienta............................................................................................ 74
5.3.3.2
Descripción del algoritmo...................................................................................................... 78
5.3.3.3
Cálculo de variables para unas condiciones de funcionamiento dadas.......................... 83
5.3.3.4
Desarrollo de interfaces.......................................................................................................... 85
5.3.3.5
Uso de la interfaz .................................................................................................................... 87
Ampliaciones que añade la herramienta CARHI
89
5.3.4.1
Información sobre rangos ...................................................................................................... 89
5.3.4.2
Inclusión de gráficas en la herramienta CARHI. Curvas y colinas de
rendimiento. ............................................................................................................................................... 89
5.3.4.3
Ajuste de la función volumen útil – cota mediante el uso de splines .............................. 93
5.3.4.4
Obtención de más coeficientes energéticos.......................................................................... 95
5.3.4.5
Características generales de cuencas, embalses y centrales............................................... 97
6 CONCLUSIONES........................................................................................................................... 100
7 LINKS Y BIBLIOGRAFÍA ............................................................................................................ 103
8 AGRADECIMIENTOS.................................................................................................................. 105
A CÓDIGOS DE PROGRAMACIÓN EN FORTRAN ................................................................ 108
A.1 EMBALSES.CAR ............................................................................................ 108
A.2 CENTRALES.CAR ......................................................................................... 108
A.3 CARHI.FOR..................................................................................................... 108
x
A.4 CARHICEN.FOR ............................................................................................ 110
A.5 CARHIRESTOS.FOR...................................................................................... 112
A.6 CARHICENRESTOS.FOR ............................................................................. 114
B CONTROL DE CARACTERÍSTICAS EXTRAÍDAS DEL MODHI MEDIANTE
PROGRAMACIÓN EN VISUAL BASIC ................................................................................... 117
B.1 Control de las características de embalses y centrales hidroeléctricas ... 117
B.2 Preparación y organización de las características para implementarlas
en archivos .mat.............................................................................................. 118
C CONTROL
ANALÍTICO
Y
GRÁFICO
DE
LAS
CARACTERÍSTICAS
HIDROELÉCTRICAS MEDIANTE PROGRAMACIÓN EN MATLAB.............................. 121
C.1 Función que relaciona la cota con el volumen útil y total del embalse .. 121
C.2 Función que relaciona el caudal total y la cota afterbay........................... 124
C.3 Función que relaciona el caudal unitario y la potencia de generación
unitaria............................................................................................................. 127
C.4 Función que relaciona el salto neto y la potencia unitaria máxima ........ 130
D DESARROLLO DE INTERFACES Y REALIZACIÓN DE CÁLCULOS EN EXCEL
MEDIANTE PROGRAMACIÓN EN VBA................................................................................ 133
D.1 Declaraciones .................................................................................................. 133
D.2 Búsqueda del embalse o central ................................................................... 134
D.3 Llenado de las estructuras de VBA correspondientes al embalse o
central............................................................................................................... 135
D.4 Carga de características del embalse o central ........................................... 137
D.5 Subrutinas correspondientes a las funciones del embalse ....................... 142
D.6 Subrutinas correspondientes a las funciones de la central....................... 145
D.7 Subrutinas de cálculo polinómico del embalse.......................................... 158
D.8 Subrutinas de cálculo polinómico y de interpolación simple y doble de
la central .......................................................................................................... 160
D.9 Proceso iterativo para unas condiciones de funcionamiento de una
central............................................................................................................... 165
D.10 Subrutinas en las que se apoya la iteración para unas condiciones de
funcionamiento............................................................................................... 170
xi
D.11 Subrutinas de carga y borrado de gráficas del embalse o de la central 175
D.12 Actualización de rangos de celda a los que hacen referencia los
menús desplegables ....................................................................................... 177
E AMPLIACIONES QUE CONTIENE LA HERRAMIENTA CARHI ..................................... 181
E.1 Función que relaciona el caudal por grupo con el rendimiento de la
turbina.............................................................................................................. 181
E.2 Colinas de rendimiento: relación entre el salto neto, el caudal por
grupo y el rendimiento de la turbina .......................................................... 184
E.3 Ajuste de la función volumen útil - cota mediante el uso de splines ..... 186
xii
Índice de Figuras
Nota: todas las figuras que carecen de referencia se corresponden con figuras realizadas por
el autor de la memoria de proyecto.
Figura 1. Principio fundamental de la hidrostática. Ref: 100cia.com ............................................... 10
Figura 2. Teorema de Torricelli (símil de velocidad de salida de un líquido). Ref:
www.sc.ehu.es.............................................................................................................................. 11
Figura 3. Teorema de Bernouilli. Ref: editorial.cda.ulpgc.es............................................................. 13
Figura 4. Curva que relaciona la cota con el volumen útil y total .................................................... 17
Figura 5. Vista en planta de la central de José María Oriol (se aprecian sus desagües). Ref:
Iberdrola. ....................................................................................................................................... 18
Figura 6. Curva que relaciona el salto neto con la potencia máxima de grupo .............................. 21
Figura 7. Generación de potencia eléctrica en una central. Ref: wikimedia.................................... 23
Figura 8. Curvas de nivel de rendimiento. Ref: Iberdrola ................................................................. 25
Figura 9. Sección por de una central hidroeléctrica (se aprecian sus conducciones). Ref:
www.skycrapercity.com ............................................................................................................. 27
Figura 10. Incidencia del agua en una turbina Pelton ........................................................................ 28
Figura 11. Turbina Kaplan ..................................................................................................................... 29
Figura 12. Sistema eléctrico.................................................................................................................... 33
Figura 14. Depósito superior de la central La Muela ......................................................................... 39
Figura 15. Ejemplo de la simulación de la turbinación de un embalse............................................ 41
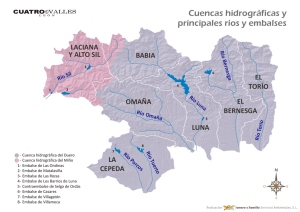
Figura 16. Cuencas hidráulicas de Iberdrola ....................................................................................... 42
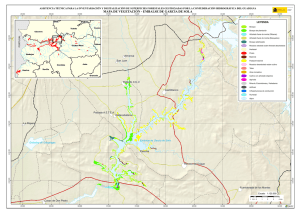
Figura 17. Plano de la cuenca del Sil..................................................................................................... 43
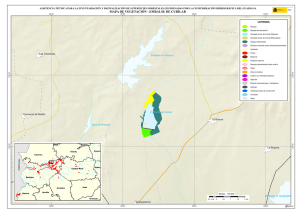
Figura 18. Embalse de la Almendra...................................................................................................... 44
Figura 19. Esquema topológico del Tajo inferior ................................................................................ 45
Figura 20. Puente romano de la presa de Alcántara........................................................................... 46
Figura 21. Presa de Alcántara ante grandes avenidas........................................................................ 46
Figura 22. Central de bombeo puro La Muela..................................................................................... 47
Figura 23. Menú principal del Modelo Hidráulico (MODHI)........................................................... 52
Figura 24. Proceso de programación en Fortran para extraer datos del MODHI .......................... 53
Figura 25. Control de características extraídas del MODHI mediante programación en Visual
Basic ............................................................................................................................................... 58
Figura 26. Relación entre Excel, Visual Basic y Matlab en la herramienta CARHI ........................ 61
Figura 27. Curva que relaciona la cota con el volumen útil y el volumen total de un embalse ... 62
Figura 28. Curva que relaciona el caudal total con la cota de desagüe de la central ..................... 65
Figura 29. Impacto del cuenco amortiguador en la curva que relaciona caudal turbinado y
vertido con la cota afterbay ........................................................................................................ 66
xiii
Figura 30. Cuenco amortiguador. Ref: www.skyscrapercity.com.................................................... 67
Figura 31. Relación entre el caudal unitario y la pérdida de carga en una central donde los
grupos comparten conductos ..................................................................................................... 68
Figura 32. Relación entre el caudal unitario y la pérdida de carga en una central donde los
grupos no comparten conductos................................................................................................ 69
Figura 33. Curva que relaciona el caudal unitario y la potencia de generación unitaria .............. 70
Figura 34. Función que relaciona el salto neto con la potencia máxima unitaria ........................... 72
Figura 35. Algoritmo de la herramienta CARHI................................................................................. 78
Figura 36 . Procesamiento del algoritmo.............................................................................................. 80
Figura 37. Procedimientos de las hojas de embalses y centrales de CARHI................................... 80
Figura 38. Interpolación doble............................................................................................................... 82
Figura 39. Iteración para unas condiciones de funcionamiento de una central.............................. 85
Figura 40. Menús desplegables y botones de comando del CARHI ................................................ 86
Figura 41. Botones de selección del CARHI ........................................................................................ 86
Figura 42. Mensaje de aviso en la herramienta CARHI ..................................................................... 87
Figura 43. Rangos que proporciona la herramienta CARHI ............................................................. 89
Figura 44. Curvas de rendimiento en relación al caudal por grupo y al salto neto ....................... 90
Figura 45. Diferencia de salto que abarcan las curvas de nivel de rendimiento............................. 91
Figura 46. Colina de rendimiento ......................................................................................................... 92
Figura 47. Comparativa entre un ajuste de 5º grado y un ajuste spline........................................... 94
Figura 48. Ajuste spline .......................................................................................................................... 95
Figura 49. Distintos coeficientes energéticos ....................................................................................... 96
Figura 50. Impresión de pantalla de características generales de una cuenca ................................ 98
xiv
Índice de Ecuaciones
Ecuación 1. Caudal.................................................................................................................................... 8
Ecuación 2. Caudal bis.............................................................................................................................. 8
Ecuación 3. Ley de continuidad .............................................................................................................. 9
Ecuación 4. Peso ...................................................................................................................................... 10
Ecuación 5. Fuerza de empuje ............................................................................................................... 10
Ecuación 6. Principio fundamental de la hidrostática........................................................................ 10
Ecuación 7. Velocidad de caída libre .................................................................................................... 11
Ecuación 8. Teorema de Torricelli......................................................................................................... 11
Ecuación 9. Teorema de Bernouilli en una situación ideal ................................................................ 12
Ecuación 10. Pérdida de carga ............................................................................................................... 13
Ecuación 11. Potencia.............................................................................................................................. 22
Ecuación 12. Rendimiento total ............................................................................................................. 24
Ecuación 13. Rendimiento de bombeo ................................................................................................. 24
Ecuación 14. Rendimiento total bis....................................................................................................... 24
Ecuación 15. Rendimiento de la turbina .............................................................................................. 24
Ecuación 16. Producible hidráulico ...................................................................................................... 25
Ecuación 17. Coeficiente energético...................................................................................................... 26
Ecuación 18. Beneficio social neto ......................................................................................................... 33
Ecuación 19. Relación entre la cota y el volumen útil y total ............................................................ 63
Ecuación 20. Salto neto teórico .............................................................................................................. 73
Ecuación 21. Interpolación doble .......................................................................................................... 82
Ecuación 22. Ecuaciones de pesos de la interpolación doble ............................................................ 83
xv
Índice de Tablas
Tabla 1. Clasificación de algunos embalses en las cuencas del Duero y Tajo ................................. 15
Tabla 2. Funciones extraídas por los distintos códigos de Fortran................................................... 54
Tabla 3. Variables y características asociadas en la extracción de datos con Fortran (archivos
CARHI.FOR y CARHICEN.FOR).............................................................................................. 55
Tabla 4. Características generales extraídas mediante el archivo CARHIRESTOS.FOR de
Fortran ........................................................................................................................................... 55
Tabla 5. Características generales extraídas mediante el archivo CARHICENRESTOS.FOR de
Fortran ........................................................................................................................................... 56
Tabla 6. Características de explotación de los embalses del CARHI................................................ 75
Tabla 7. Características generales y de explotación de las centrales del CARHI ........................... 76
Tabla 8. Características generales de los embalses del CARHI......................................................... 77
1
Introducción
1 Introducción
1
1.1
2
Introducción
Motivación
Para valorar una obra en su justa medida, es necesario un conocimiento profundo
de las motivaciones que impulsaron al autor de la misma a llevarla a cabo.
El germen de la motivación surge en 2005, cuando al comenzar 3º de carrera me
decanté por la rama eléctrica de Ingeniería Industrial. Tenía dudas cuando tomé la
decisión porque las otras ramas (mecánica y electrónica) también me llamaban mucho
la atención. No obstante, a medida que transcurría el tiempo constaté que había sido la
decisión adecuada, puesto que los conocimientos específicos que estaba adquiriendo en
la materia eléctrica eran ciertamente atractivos.
Acabé el curso con éxito y gracias a ello, a mi insistencia en la oficina de Relaciones
Internacionales de ICAI y a la suerte, pude cursar 4º de carrera becado como estudiante
de intercambio en Case Western Reserve University, Ohio (USA), donde tuve la
oportunidad de seguir ampliando mis conocimientos del tema eléctrico, y pude
observar una metodología de trabajo diferente, pero igualmente enriquecedora.
Entre otras maravillosas actividades que realicé ese año, tuve la oportunidad de
formar parte del equipo universitario de Ingenieros Sin Fronteras – EE.UU.
Desarrollamos a lo largo del año un proyecto de suministro de agua a la comunidad de
Cruce de Blanco, situada en las montañas del centro de la República Dominicana. La
primera fase del proyecto se hizo efectiva en marzo de 2007: doce estudiantes y dos
profesores viajamos al lugar del proyecto. Estuvimos trabajando una semana y los
resultados fueron un éxito. Posiblemente el proyecto de canalización de agua se finalice
este año. El caso es que cuando viajé a Cruce de Blanco descubrí que la comunidad no
siempre había carecido de agua. Achacaban la disminución o desaparición del caudal
de los ríos aledaños a la construcción de varias presas y embalses en las proximidades
de la zona. No sé si esa es la razón o una de las razones de su falta de agua, pero lo
importante es que por primera vez en mi vida me di cuenta de que mi formación y los
conocimientos que adquiero en el estudio tienen sentido en la realidad y en la
sociedad, bien sea ayudando a otras personas a disfrutar de un bien tan básico como es
1 Introducción
3
el agua, bien sea construyendo presas y embalses con cuidado de no perjudicar a otras
personas o al medio ambiente.
A medida que se acercaba el final del curso 2006 – 2007 en Estados Unidos, empecé
a sentir cierta inquietud por la elección de un proyecto fin de carrera. No me
encontraba en España, por lo que me preocupaba que hubiera proyectos interesantes
de los que no supiera. Me informé debidamente y decidí buscar un proyecto que fuera
acorde con la especialidad que llevaba cursando dos años, es decir, un proyecto
relacionado con aspectos eléctricos, y que a ser posible estuviera relacionado con la
gestión hidroeléctrica, ya que se trataba de un tema que personalmente me interesaba
después de la experiencia con Ingenieros Sin Fronteras.
Mi alegría y suerte fue grande cuando supe de este proyecto sobre el modelado las
características de embalses y centrales hidroeléctricas. Se trataba de un proyecto muy
interesante, que se ajustaba a mis cualidades personales y de trabajo, y que era
compatible con mis estudios en el ICAI.
Pasé las pruebas de selección de Iberdrola, me entrevisté con mis potenciales
directores de proyecto, y finalmente me fue asignado un contrato como becario
durante ocho meses en los que creo haber realizado un buen proyecto, que ha
resultado ser tanto útil como herramienta de trabajo, puesto que su aplicación es
inmediata en Iberdrola, como enriquecedor en el ámbito académico y personal.
1.2
Descripción del problema
Este proyecto surge como una necesidad de desarrollo de una aplicación que
modele las características de embalses y centrales hidroeléctricas, sirviendo como
herramienta para la optimización y gestión de recursos hidroeléctricos que lleva a cabo
el departamento de Planificación y Ofertas (PYOFE) de Iberdrola.
Hasta el momento Iberdrola hacía uso del programa llamado Modelo Hidráulico
(MODHI) como herramienta fundamental de almacenamiento y cálculo de
características de embalses y centrales hidroeléctricas. Este programa constituye, junto
con otras herramientas, la base en la que se apoya la optimización y la gestión del agua.
El MODHI funciona en una versión del sistema operativo VMS. El acceso al mismo es
únicamente a través de un emulador de una consola de VAX - VMS, y la extracción de
1 Introducción
4
datos así como el manejo de las funciones que contiene se tiene que hacer
fundamentalmente mediante programación en el lenguaje Fortran o por pantalla.
El sistema operativo VMS y la programación en Fortran eran ventajosos en tanto en
cuanto a que la velocidad de cálculo es casi instantánea, se cuida al extremo detalles
como la capacidad de memoria o la longitud de las variables, y la forma de organizar
los datos y estructurar los códigos es rigurosa y óptima. Sin embargo, hoy en día puede
resultar tedioso el manejo de un programa en este entorno, puesto que en la mayoría
de las empresas la optimización y la planificación se realizan en entornos de Excel y
Matlab, usando lenguajes de programación como Visual Basic for Applications.
Por tanto, el proyecto consiste en la elaboración de una herramienta en Excel
llamada Características Hidroeléctricas (CARHI) que sustituya al MODHI. No sólo lo
sustituye en el sentido estricto de la palabra, sino que también lo mejore y lo amplíe. El
CARHI es una aplicación que se desarrolla en Excel para que los datos y resultados que
proporciona sean más fácilmente exportables a programas de planificación y
optimización que también están desarrollados en Excel.
Se trata de un proyecto que combina el estudio científico de las características de los
embalses y las centrales con el trabajo práctico en una empresa, adaptando una
herramienta a las necesidades de planificación y optimización de unos recursos
hidroeléctricos.
1.3
Objetivos y estructura del proyecto
Como se ha comentado anteriormente, el objetivo de este proyecto es la elaboración
de una herramienta informática llamada Características Hidroeléctricas (CARHI) que
proporcione datos de las características de los embalses y centrales de Iberdrola, y
realice cálculos con ellos que posteriormente se usarán en otras herramientas de
planificación y optimización de los recursos hidráulicos.
Para llevar a cabo este objetivo se han realizado una serie de pasos, estructurados
del siguiente modo:
1 Introducción
1.3.1
5
Estudio de conceptos hidráulicos y de aspectos relacionados con la gestión de recursos
hidroeléctricos
En primer lugar, es necesario familiarizarse con los conceptos físicos y matemáticos
que se van a manejar. Los conocimientos aprehendidos hay que tenerlos presentes a lo
largo del proyecto para no perder nunca la perspectiva del sentido real que tienen los
datos que se manejan y los códigos que se programan. Aparte de no perder la
perspectiva, también es necesario disponer de estos conocimientos a la hora de filtrar
posibles errores que pudiera haber en la extracción de datos del MODHI o que
simplemente fueran consecuencia de ruido introducido al programar en Fortran.
Este estudio de conceptos hidráulicos se describe en el capítulo 2.
Asimismo, una vez se han aprehendido los conceptos hidráulicos básicos, es
necesario realizar un repaso acerca de aspectos retributivos que afectan a la generación
hidroeléctrica en concreto, así como también se requiere profundizar en conceptos
técnicos y de gestión aplicados particularmente a embalses y centrales hidroeléctricas
pertenecientes a Iberdrola.
Estos aspectos retributivos y de gestión hidroeléctrica se tratan en los capítulos 3 y
4, respectivamente.
1.3.2
Programa MODHI: extracción y control de datos mediante programación en Fortran y
en Visual Basic for Applications
El siguiente paso indispensable en el proyecto es la extracción de toda la
información contenida en el MODHI. El lenguaje de programación más apropiado para
llevar a cabo ese trabajo es Fortran, puesto que el MODHI funciona en una versión
antigua del sistema operativo VMS. Una vez se ha extraído la información y está
disponible en archivos de tipo texto, se ha de pasar a hojas de Excel donde el manejo es
mucho más versátil y cómodo. Para ello es necesario organizar y controlar los datos
mediante programación en Visual Basic for Applications (VBA), ya que la cantidad de
información que se maneja es inmensa, siendo imposible hacer a mano la transferencia
de los datos y la detección de ruido generado durante su extracción.
Estos pasos de extracción y control de datos mediante programación en Fortran y
Visual Basic se han descrito en el capítulo 5, concretamente a lo largo del apartado 5.2.
1 Introducción
1.3.3
6
Tratamiento analítico y gráfico de características hidroeléctricas en Matlab
Una vez se tiene organizada y controlada toda la información necesaria es preciso
comprobar que es correcta y filtrar adecuadamente el ruido y los errores derivados de
la extracción. Se ha considerado oportuno llevar a cabo este trabajo en Matlab, ya que
desde el punto de vista del autor el lenguaje de programación que se usa en Matlab es
el más intuitivo de los que ofrece el mercado, así como su capacidad de análisis gráfica
se encuentra entre las más rápidas de las que existen actualmente. Asimismo, el trabajo
realizado en Matlab no sólo ha servido para realizar un control de los datos, sino
también para aportar valor añadido a la herramienta CARHI, por dos motivos
fundamentales: los rangos de funcionamiento de las características hidroeléctricas y la
carga de gráficas provienen del estudio realizado mediante programación en Matlab.
Este trabajo de control de datos y aporte de valor añadido mediante programación
en Matlab se describe en el capítulo 5, concretamente en el apartado 5.3.2.
1.3.4
Diseño y modelado de la herramienta CARHI
Como ya se ha comentado en el apartado 1.2, la herramienta CARHI es un
aplicación que actualiza y amplia al programa MODHI. CARHI hace las veces de base
de datos y de plataforma de cálculo de variables de embalses y centrales
hidroeléctricas. La aplicación se ha desarrollado en el entorno Excel mediante
programación en Visual Basic for Applications (VBA). Dicha programación permite
tanto el manejo y cálculo de funciones a partir de las variables que caracterizan a los
embalses y centrales de Iberdrola como el desarrollo de interfaces que faciliten el
trabajo a los usuarios de la herramienta.
Cabe mencionar que el CARHI proporciona los mismos datos, variables y
resultados que
se obtenían en el MODHI, pero mediante procesos y códigos de
programación completamente distintos. Asimismo, contiene varias ampliaciones
importantes que no existían en la anterior herramienta.
Este trabajo de diseño de una herramienta para el modelado de características
hidroeléctricas se describe en el capítulo 5. Concretamente en el apartado 5.3.3 se
detalla la organización y el funcionamiento de la herramienta CARHI, así como la
estructura del código en VBA en el cual se apoya, y en el apartado 5.3.4 se describen las
ampliaciones del CARHI respecto del MODHI.
2
Conceptos hidráulicos
2 Conceptos hidráulicos
2
2.1
8
Conceptos hidráulicos
Introducción
Se ha considerado oportuno empezar por un capítulo que resuma los conceptos
hidráulicos básicos, necesarios para seguir con comodidad la lectura del resto de los
capítulos. La primera parte de este capítulo se centra en conceptos de la física de los
líquidos en general (ver apartados 2.2 y 2.3), mientras que la segunda parte entra más
en detalle con conceptos relacionados con embalses y centrales, que es lo que concierne
concretamente al proyecto (ver apartados 2.4 y 2.5)
2.2
Definiciones
Nivel: horizontalidad de la superficie líquida.
Cota: altura a la que se encuentra una superficie respecto del nivel del mar.
Caudal (Q): volumen de fluido (V) que atraviesa una superficie en la unidad de
tiempo (t):
Q=
V
t
⎡ m3 ⎤
⎢ ⎥
⎣ s ⎦
Ecuación 1. Caudal
⎡
m m3 ⎤
Q = A × v ⎢m 2 × =
⎥
s
s ⎦
⎣
Ecuación 2. Caudal bis
Aforo: operación por la cual se mide el caudal.
En la gestión del agua se hace uso de otro término que no se debe confundir con el
caudal. Se trata de la aportación y su definición es la siguiente:
2 Conceptos hidráulicos
9
Aportación: volumen ( m 3 ) de agua recibido por un embalse en un periodo de
tiempo determinado. Debido a que se está manejando volumen y tiempo, a veces la
aportación se puede expresar en unidades de
2.3
m3
.
s
Ecuaciones básicas
En este apartado se va a realizar un recorrido por las ecuaciones básicas sobre
aspectos hidráulicos. Se finalizará el recorrido introduciendo el trinomio de Bernouilli,
que es uno de los principales teoremas del campo de la hidrodinámica, la parte de la
mecánica que estudia
los líquidos en movimiento. Para llegar a su ecuación es
necesario recordar primero otros principios y teoremas, algunos de los cuales se
fundamentan en la hidrostática, que es el estudio de los líquidos en reposo. Los
principios y teoremas son los siguientes:
2.3.1
Ley de continuidad
La cantidad de líquido, o caudal, que circula por las distintas secciones de una
conducción en un instante dado es siempre constante, en el caso de régimen
permanente.
Del enunciado anterior se obtiene que las velocidades del líquido son inversamente
proporcionales a las secciones por las que circula:
Q1 = Q2 ⇒ S1 × v1 = S 2 × v 2
Por tan to :
S1 v 2
=
S 2 v1
Ecuación 3. Ley de continuidad
2.3.2
Principio fundamental de la hidrostática
La presión (p), en un punto de un líquido en reposo, ejercida por el propio líquido,
es igual al peso de la columna del líquido, de base la unidad y de altura la distancia (h)
desde el punto a la superficie libre.
2 Conceptos hidráulicos
10
Recurriendo al concepto de densidad (ρ ) , que se define como la masa de un cuerpo
contenida en la unidad de volumen del mismo, se tiene que el peso (P) por unidad de
volumen de un cuerpo es el siguiente:
P = ρ×g
⎡N ⎤
⎢⎣ m 3 ⎥⎦
Ecuación 4. Peso
Donde g es la aceleración de la gravedad (9,81
m
).
s2
Así que la fuerza de empuje se corresponde con la siguiente ecuación:
Empuje = ρ × g × h × A
[N ]
Ecuación 5. Fuerza de empuje
Como la presión (p) es fuerza por unidad de superficie, se obtiene la ecuación del
principio de la hidrostática:
N ⎤
⎡
p = ρ × g × h ⎢ Pa = 2 ⎥
m ⎦
⎣
Ecuación 6. Principio fundamental de la hidrostática
Figura 1. Principio fundamental de la hidrostática. Ref: 100cia.com
2 Conceptos hidráulicos
2.3.3
11
Teorema de Torricelli
La velocidad (v) de salida de un líquido, a través de un orificio practicado en la
pared del recipiente que lo contiene, es la misma que adquiriría un cuerpo que cayese
libremente desde el nivel del líquido hasta el centro de gravedad de dicho orificio.
Se demuestra que la velocidad (v) de caída libre, sin obstáculos, de un cuerpo, es la
siguiente:
v = 2× g × h
⎡m⎤
⎢⎣ s ⎥⎦
Ecuación 7. Velocidad de caída libre
Considerando h como la distancia desde el nivel del líquido hasta el centro de
gravedad del orificio, se despeja de la Ecuación 7 obteniendo la siguiente ecuación:
h=
v2
2× g
[m]
Ecuación 8. Teorema de Torricelli
Figura 2. Teorema de Torricelli (símil de velocidad de salida de un líquido). Ref: www.sc.ehu.es
2 Conceptos hidráulicos
2.3.4
12
Teorema de Bernouilli
A continuación se procede a deducir el teorema de Bernouilli, haciendo uso de los
conceptos descritos hasta el momento.
Sea el conjunto representado de la Figura 3. Si el líquido se encontrase en reposo,
estaríamos ante un problema de hidrostática. La altura (también llamada carga) H
constante (por eso se representa con una K en la figura) sería igual a una altura Z
p
respecto de un plano de referencia más
γ
según el Principio Fundamental de la
Hidrostática, donde γ = ρ × g .
Sin embargo, si se suministra un caudal y se cumple el Principio de Continuidad, el
v2
nivel desciende, siendo dicho descenso de nivel igual a
según el Teorema de
2× g
Torricelli.
v2
que sería necesaria para producir la
2× g
Recapitulando: la altura equivalente
velocidad (caída) del líquido por el punto P de la figura se denomina altura cinética, y
la altura
p
γ
alcanzada por el líquido proporcional a la presión ejercida por la columna
de éste sobre el punto P se denomina altura piezométrica. Aparte, se considera la altura
geométrica como la altura Z existente entre el punto P y un plano horizontal de
referencia. De este modo, se obtiene que, en una situación ideal, la carga H es constante
y se corresponde con la siguiente ecuación:
H =Z+
p
γ
+
v2
= cons tan te
2× g
Ecuación 9. Teorema de Bernouilli en una situación ideal
Todas las consideraciones realizadas hasta el momento se corresponden con un
enfoque ideal de la realidad (ver Figura 3)
2 Conceptos hidráulicos
13
Figura 3. Teorema de Bernouilli. Ref: editorial.cda.ulpgc.es
En la práctica, la carga H no es constante debido a rozamientos y otros fenómenos,
por lo que se define la pérdida de carga (J) entre un punto A y un punto B aguas abajo
como:
J AB = H A − H B
Ecuación 10. Pérdida de carga
2.4
Nota: no confundir el concepto hidráulico de carga que se viene comentando en este
apartado con el término carga de grupo, entendido por la potencia que un grupo
proporciona en un instante determinado. Este concepto se desarrollará más adelante
en el apartado 2.5.5.
Características de los embalses
2.4.1
Introducción
Muchos son los aspectos que se podrían considerar al describir un embalse
(superficie de cuenca, superficie del embalse, términos municipales afectados, etc.) o al
describir su presa (tipo de presa, cota de coronación, longitud de coronación, hormigón
utilizado, capacidad de vertido, etc.). No obstante, en este capítulo se indicarán
únicamente aquellos aspectos considerados más relevantes y que permiten desarrollar
el resto de los capítulos de esta memoria de proyecto.
2 Conceptos hidráulicos
2.4.2
14
Tipos
Los embalses se pueden clasificar según su capacidad ( hm 3 ). No obstante, la
clasificación debe tener en cuenta no sólo la capacidad del embalse, sino también la
ratio aportación - capacidad. Esto se debe a que, por ejemplo, un embalse puede tener
una gran capacidad y en principio considerarse de régimen anual (como se comentará
a continuación), pero si recibe una gran aportación, es decir, tarda poco tiempo en
llenarse, entonces posiblemente su régimen sea semanal. Según este criterio los
embalses se pueden clasificar en:
Embalses de régimen diario/semanal: los de régimen diario son aquéllos en los
que la gestión de sus aportaciones nos permite parar unas horas del día (p.e. en horas
valle) y los de régimen semanal se puede parar un día o dos a la semana (p.e. sábados
y domingos).
Embalses de régimen anual: son aquéllos en los que se realiza la gestión de sus
aportaciones a lo largo del año con el objeto de la optimización hidroeléctrica, la cual
puede estar basada en un incremento del riesgo de vertido para vender más tarde
cuando el precio de la electricidad es mayor, en evitar vertidos, etc. En este tipo de
embalses el nivel al principio y final del año hidrológico (octubre a septiembre) suele
ser similar.
Embalses de régimen hiperanual: son aquéllos en los que se realiza la gestión de
sus aportaciones a lo largo varios años con el objeto de la optimización hidroeléctrica.
Se diferencian de los embalses de régimen anual en cuanto a que tienen capacidad para
gestionar sus aportaciones de forma que las embalsadas en un año hidrológico pueden
no ser desembalsadas durante el mismo año. En este tipo de embalses el nivel al
principio y final del año hidrológico (octubre a septiembre) puede ser muy diferente.
A continuación se muestra unas tablas con la clasificación de algunos embalses de
las cuencas de Iberdrola en el Duero y el Tajo:
2 Conceptos hidráulicos
DUERO
15
TAJO
EMBALSE
RÉGIMEN
EMBALSE
RÉGIMEN
CERNADILLA
ANUAL (RIEGOS)
AZUTAN
DIARIO/SEMANAL
VALPARAISO
DIARIO/SEMANAL
VALDECAÑAS
ANUAL
AGAVANZAL
DIARIO/SEMANAL
RICOBAYO
ANUAL
Tabla 1. Clasificación de algunos embalses en las cuencas del Duero y Tajo
2.4.3
Cota
Cota máxima de explotación normal: nivel máximo que puede alcanzar la cota del
embalse en situación de avenida no extraordinaria. El nivel del embalse no deberá
elevarse por encima de la cota máxima normal antes de que todos los órganos de
desagüe estén completamente abiertos. Se mide en metros sobre el nivel del mar
(msnm).
Cota máxima extraordinaria: nivel máximo que puede alcanzar la cota del embalse
en situación de avenida extraordinaria, teniendo abiertos todos los órganos de desagüe
desde que se alcanzó la cota máxima de explotación normal. Por tanto, la cota máxima
extraordinaria tiene un carácter estructural, no de gestión. Se mide en metros sobre el
nivel del mar (msnm).
Cota mínima de explotación normal: nivel mínimo al que se puede turbinar. En
algunos embalses esta cota no supone un límite mínimo físico de turbinación, sino que
existe un límite de otro tipo como puede ser la refrigeración de una central nuclear (si
se baja demasiado el nivel, cabe la posibilidad de que la toma de refrigeración se
quedara seca). Se mide en metros sobre el nivel del mar (msnm).
2.4.4
Curvas de resguardo
Se trata de una curva temporal que determina la cota máxima que se permite en un
momento determinado sin que haya vertido. Su objeto es tener un volumen de
prevención de una posible avenida, de tal modo que si se rebasa, se ha de empezar a
verter en un determinado porcentaje para que en el caso de llegar a un nivel de cota
máxima, no haya que verter bruscamente.
2 Conceptos hidráulicos
2.4.5
16
Curva de garantía (o de hierro)
Se trata de una curva que determina un nivel variable a lo largo del año, cuyo
cumplimiento garantiza que se darán los riegos y los abastecimientos anuales con una
determinada probabilidad (p.e., 99% de probabilidad). Sólo se puede turbinar si la cota
está por encima de la curva. Si se está por debajo de ella, sólo se podrá turbinar si se
necesita suministro aguas abajo para riegos o abastecimiento. Si el nivel es
extremadamente bajo, será imposible turbinar, por lo que el agua tendrá que salir por
los desagües de fondo (ver el apartado 2.4.7). Esta cota constituye una restricción
importante a la hora de la gestión del agua en el embalse.
2.4.6
Volúmenes
Capacidad máxima o volumen máximo: volumen máximo almacenado en el
embalse cuando se encuentra a su cota máxima. Se mide en m 3 (ó hm 3 debido a las
grandes cantidades de agua en los embalses).
Volumen muerto o volumen mínimo: volumen almacenado en el embalse cuando se
encuentra a su cota mínima. Se corresponde con la cantidad de agua que no puede ser
turbinada en la central asociada al embalse, aunque constituye una reserva que puede
ser turbinada en las centrales aguas abajo. Se mide en m 3 (ó hm 3 debido a las grandes
cantidades de agua en los embalses).
Volumen útil: volumen almacenado en el embalse y que puede ser turbinado en la
central asociada al mismo. Se mide en m 3 (ó hm 3 debido a las grandes cantidades de
agua en los embalses).
A continuación se observa la Figura 4, donde se tiene la curva cota – volumen útil
superpuesta con la curva cota – volumen total. Se observa que efectivamente el
volumen total es el volumen útil más una constante (volumen muerto).
2 Conceptos hidráulicos
17
Figura 4. Curva que relaciona la cota con el volumen útil y total
2.4.7
Desagües
Los desagües que se denominan aliviaderos evitan que el agua en exceso,
procedente de grandes crecidas, rebose sin control por encima de las presas, lo cual
podría ocasionar grandes daños, poniendo en peligro la estabilidad de las mismas al
presentarse esfuerzos y efectos perjudiciales.
Los aliviaderos se encuentran principalmente formando parte íntegra de la presa,
mediante aberturas ubicadas en la coronación. Encauzan el agua, llegándose en
situaciones normales a regular la cantidad de los caudales vertidos.
Por razones similares se instalan otro tipo de desagües conocidos como desagües de
fondo y desagües de medio fondo. Éstos se sitúan a media altura de la presa,
generalmente en los laterales, mientras que aquéllos están cerca de la cimentación. Los
desagües de medio fondo sirven de ayuda a los aliviaderos y los desagües de fondo se
usan como medio de seguridad en el vaciado total del embalse.
2 Conceptos hidráulicos
18
Figura 5. Vista en planta de la central de José María Oriol (se aprecian sus desagües). Ref: Iberdrola.
2.5
Características de las centrales hidroeléctricas
2.5.1
Introducción
En general, las centrales hidroeléctricas son bastante rentables, pues si bien su coste
inicial de construcción es elevado, una vez puestas en funcionamiento los gastos de
explotación y mantenimiento son relativamente bajos, siempre y cuando las
condiciones pluviométricas medias del año sean plenamente favorables. También se ha
de considerar su impacto ambiental, y los costes sociales derivados del mismo.
De manera análoga al apartado anterior que trata sobre características de los
embalses, muchas son las características propias de cada central. No obstante, en este
apartado se indicarán aquellos aspectos que se consideran más relevantes y que
permiten desarrollar el resto de los capítulos de esta memoria de proyecto.
2 Conceptos hidráulicos
2.5.2
19
Tipos
Son varios los argumentos que aportan datos para realizar una clasificación,
suficientemente explícita, de las centrales, en función de características técnicas,
peculiaridades de asentamiento y condiciones de funcionamiento.
En primer lugar, hay que distinguir las que utilizan agua según discurre
normalmente por el cauce del río, y aquellas otras a las que ésta llega,
convenientemente regulada, desde un embalse. Se denominan respectivamente:
•
Centrales de agua fluyente: no cuentan prácticamente de reserva de agua,
aunque se construyen formando una presa para mantener el desnivel
(constante) de agua. En temporada de precipitaciones pueden hasta dejar
pasar agua excedente para que no sea superada su potencia máxima (ver
apartado 2.5.5)
•
Centrales de agua embalsada: el agua se utiliza según la demanda a través
de conductos (ver apartado 2.5.8) que la encauzan hacia las turbinas (ver
apartado 2.5.9)
A su vez, y dentro de las centrales de agua embalsada, se tienen las:
•
Centrales de regulación: típica central de agua embalsada. Se adapta muy
bien para cubrir horas punta de la demanda.
•
Centrales de bombeo: acumulan caudal mediante bombeo a embalse
superior. El bombeo lo realiza una bomba, que puede ser una máquina
independiente o una turbina reversible, durante las horas nocturnas. Esto lo
hace rentable porque de noche el agua es más barata que de día. Podemos
considerar dos tipos de centrales de bombeo:
9 Centrales de bombeo puro: son aquellas en las que el embalse al que se sube
el agua carece de aportación hidráulica natural.
9 Centrales de bombeo mixto: son aquellas en las que el embalse al que se sube
el agua sí posee aportación hidráulica natural.
Asimismo, y en relación con la altura del salto (ver apartado 2.5.3) de agua existente
se tienen los siguientes tipos de centrales:
2 Conceptos hidráulicos
•
20
Centrales de alta presión: se suelen corresponder con centrales situadas en
zonas de alta montaña donde se aprovecha el agua proveniente de lagos
naturales. Sus grupos suelen ser Pelton o Francis, su salto hidráulico es del
orden de 200 m y su caudal es del orden de 20
•
m3
.
s
Centrales de media presión: se suelen corresponder con centrales situadas en
zonas de media montaña o valles donde se aprovecha el agua de grandes
embalses. Sus grupos suelen ser Francis o Kaplan, su salto hidráulico es del
orden de entre 20 y 200 m y su caudal es del orden de 200
•
m3
.
s
Centrales de baja presión: se suelen corresponder con centrales situadas
valles amplios. Sus grupos suelen ser Kaplan, su salto hidráulico es del
orden de menos de 20 m y su caudal es del orden de más de 300
2.5.3
m3
.
s
Nota: ya adelantamos que la potencia es directamente proporcional al
producto del caudal por el salto neto (ver apartado 2.5.6). Por tanto, nos
percatamos que la potencia en las centrales de alta, media y baja presión es
similar, ya que unas tienen gran caudal y pequeño salto, y otras tienen
pequeño caudal y gran salto neto.
Saltos
Se denomina salto de agua al paso brusco o caída de masas de agua desde un nivel,
más o menos constante, a otro inmediatamente inferior. Numéricamente se identifica
por la diferencia de cota, o de nivel, lo que llamamos altura de salto o salto
simplemente, cuyo valor se da en metros (m). Se puede distinguir entre salto bruto y
salto neto:
Salto bruto: diferencia entre cota agua embalsado y cota de la corriente de agua que
se establece una vez ésta ha recorrido todas las conducciones de la central (nivel de
desagüe o cota afterbay). También recibe el nombre de salto real.
Salto neto: en el caso de turbinación, el salto neto es el salto bruto menos las
pérdidas de carga (m) originadas por el paso del agua por la cámara de carga, tubería
forzada y sus accesorios (ver apartado 2.3.4).
2 Conceptos hidráulicos
21
Sin embargo, en el caso de bombeo, como se lleva el agua a una altura superior,
el salto neto es el salto bruto (físico) que hay que superar más la pérdida de carga
debida al rozamiento del sistema hidráulico. Por tanto, en el caso de bombeo tenemos
que, si los grupos se influyen los unos a los otros porque comparten conductos, se
puede estar bombeando con un número determinado de grupos, y sí se pasa a
bombear con un grupo más, éste introduce una pérdida de carga adicional que hace
que todos los grupos ya no sean capaces de vencer la diferencia de cotas.
Figura 6. Curva que relaciona el salto neto con la potencia máxima de grupo
2.5.4
Caudal y aportación
En el apartado 2.2 se definieron los conceptos de caudal y aportación. A continuación
se entrará en un mayor detalle:
Caudal máximo turbinable: es la capacidad de turbinación de la central en la
situación de explotación en que se encuentre.
Caudal natural: se corresponde con la cantidad de agua que llegaría al embase
suponiendo que no ha sido retenida en los embalses situados aguas arriba. Se suele
hm 3
m3
, aunque en Iberdrola se mide en
porque se trata de una unidad
medir en
día
s
más intuitiva a la hora de ver lo que ocurre en un instante determinado de tiempo.
2 Conceptos hidráulicos
22
Aportación real: se corresponde con la cantidad de agua en m 3 que realmente llega
al embalse teniendo en cuenta turbinados y vertidos en centrales aguas arriba, riegos,
bombeos, etc.
Aportación de cuenca intermedia: es la aportación en m 3 que llega al embalse sin
tener en cuenta las salidas de turbinados y vertidos en centrales situadas aguas arriba.
2.5.5
Potencia
La potencia se define como la cualidad que determina la mayor o menor rapidez en
realizar un trabajo. Por tanto, la potencia también se puede definir como la cantidad de
energía absorbida en la unidad de tiempo.
P=
E
t
[W ]
Ecuación 11. Potencia
A continuación se darán una serie de definiciones básicas:
Potencia instalada de cada grupo: es la potencia correspondiente con la potencia
nominal. A efectos de explotación se considera la potencia neta.
Potencia disponible: esta potencia depende no sólo del número de grupos
disponibles en cada central sino del salto neto en cada momento y del régimen de
funcionamiento de la turbina. En los estudios de explotación se consideran
básicamente dos tipos de funcionamiento que nos relacionan potencia, caudal
turbinado y altura del salto:
•
Funcionamiento en calidad de máximo rendimiento o funcionamiento a
potencia óptima: es el que se utiliza normalmente.
•
Funcionamiento de máxima admisión: se utiliza en aquellas ocasiones
en que es necesario turbinar el máximo para evitar vertidos aunque el
rendimiento energético sea algo menor.
•
Funcionamiento en regulación: condiciones intermedias entre un
funcionamiento
en
calidad
de
funcionamiento de máxima admisión.
máximo
rendimiento
y
un
2 Conceptos hidráulicos
23
Potencia mínima: es la menor potencia que genera el grupo pudiendo mantenerla de
forma estable, es decir, sin presentar vibraciones, cavitaciones, etc. (ver apartado 2.5.9)
Capacidad de regulación: es el rango entre potencia máxima y potencia mínima. Se
trata de una característica básica para la participación del grupo en la regulación
secundaria, que es la potencia que podría aporta el grupo en un tiempo de 100
segundos. Aparte de la regulación secundaria, el grupo posee la regulación primaria
que forma parte de las características del grupo y que una vez ajustada responde
automáticamente y de forma instantánea a la regulación frecuencia-potencia. Por
último, como regulación terciaria se entiende aquella potencia que puede generar el
grupo en un tiempo de 15 minutos. En el caso de los grupos hidráulicos coincide con la
potencia máxima.
Figura 7. Generación de potencia eléctrica en una central. Ref: wikimedia
2.5.6
Rendimiento
El concepto de rendimiento está íntimamente relacionado con el aprovechamiento o
la productividad. Se expresa siempre como el cociente de dos magnitudes, siendo el
numerador la magnitud real que se mide en la práctica y el denominador la magnitud
teórica que se obtiene mediante cálculos físicos y matemáticos, siempre mayor que la
magnitud medida. Por tanto, el rendimiento siempre será menor que la unidad, siendo
mejor cuanto más cerca esté de 1.
2 Conceptos hidráulicos
24
Centrándose en las centrales hidroeléctricas, y concretamente en las turbinas, el
rendimiento se puede expresar en base a los tres conceptos estudiados en los apartados
anteriores de este capítulo: salto neto (Hn), caudal (Q) y potencia (P). Así queda la
ecuación del rendimiento total del siguiente modo:
η=
P
ρ * g * Hn * Q
[•]
Ecuación 12. Rendimiento total
Donde ρ es la densidad del agua (1000
(9,81
kg
) y g es la aceleración de la gravedad
m3
m
), ambos constantes. Asimismo, el numerador suele recibir el nombre de
s2
potencia instantánea y el denominador suele recibir el nombre de potencia de salto.
Nota: en el caso de bombeo, como el salto neto es mayor que el salto bruto
(ver apartado 2.5.3), el rendimiento queda así:
ηbombeo =
ρ * g * Hn * Q
Pbombeo
[•]
Ecuación 13. Rendimiento de bombeo
El rendimiento total se puede expresar a su vez del siguiente modo:
η = ηturbina *ηalternador
[•]
Ecuación 14. Rendimiento total bis
De tal forma que el rendimiento de la turbina es el siguiente:
ηturbina =
P
ρ * g * Hn * Q *ηalternador
Ecuación 15. Rendimiento de la turbina
[•]
2 Conceptos hidráulicos
25
En la Figura 8 se observan unas curvas de rendimiento constante. Notar que la
curva de máxima apertura de distribuidor se corresponde con la curva que relaciona
salto neto con potencia límite de la Figura 6.
Figura 8. Curvas de nivel de rendimiento. Ref: Iberdrola
2.5.7
Coeficiente energético y producible hidráulico
El producible hidráulico (también llamado energía producible) se define como la
cantidad máxima de energía eléctrica que teóricamente se podría producir
considerando las aportaciones hidráulicas registradas, manteniendo las cotas de los
embalses, durante un determinado período de tiempo y una vez deducidas las
detracciones de agua realizadas para riego o para otros usos distintos de la producción
de energía eléctrica. Como los embalses suelen modificar su cota, una forma de calcular
el producible es a través de la siguiente ecuación:
Producible = Producción + Pérdidas Turbinales
+
Variación energía embalsada −
Energía embalsada por bombeo [GWh]
Ecuación 16. Producible hidráulico
2 Conceptos hidráulicos
26
Se entiende la energía embalsada por bombeo como el producto del bombeo por el
rendimiento del ciclo de bombeo (en torno al 70% de rendimiento)
A continuación se procede a definir el coeficiente energético:
El coeficiente energético es la relación entre la energía producida y el caudal
turbinado.
Su valor depende básicamente de la cota de embalse, del caudal turbinado y del tipo
de funcionamiento de la central, siendo su ecuación la siguiente:
c.e. =
P
Q
⎡ kWh ⎤
⎢⎣ m 3 ⎥⎦
Ecuación 17. Coeficiente energético
2.5.8
Conducciones de agua
A esta denominación genérica le corresponden todos los conductos y equipos afines
que se encuentran ubicados entre el embalse y el desagüe en el extremo inferior del
cauce.
El mejor modo de intentar alcanzar el valor de la potencia teórica del salto se logra
evitando, en la medida de lo posible, las pérdidas inútiles de energía. Para ello, los
encauzamientos de agua han de favorecer el movimiento de la misma, que deberá fluir
regularmente y con la mínima turbulencia. Es decir, sin cambios de caudal, ni
depresiones o sobrepresiones incontroladas, torbellinos, etc.
Los suministros de agua parten de las tomas de agua de la presa y discurren hacia el
pie de presa por:
•
Tuberías forzadas: encargadas de soportar grandes presiones.
•
Canales/túneles: desembocan en depósitos de carga, a partir de los cuales
derivan a su vez tuberías forzadas. Los canales son conductos abiertos, por
lo que el agua discurre en régimen libre, es decir, sometida a presión
atmosférica, por lo que se mueve por acción de la gravedad, siendo
necesario un desnivel continuo. Sin embargo, en los túneles el agua discurre
en régimen forzado, por lo que el desplazamiento del fluido se produce
2 Conceptos hidráulicos
27
debido a la presión de éste, pudiendo ser la pendiente ascendente o
descendente.
El agua puede discurrir hacia centrales de derivación por largas galerías de presión
de poca pendiente que desembocan en un depósito de carga, a partir de la cual derivan
tuberías forzadas.
Nota: en este último caso, el salto bruto de la central se ha de considerar
desde la cota de la torre de toma, no desde la cota de donde parten las largas
galerías de presión.
Una vez el agua ha discurrido por las tuberías forzadas, llega a la turbina. Antes y
después de la turbina, hay chimeneas de equilibrio, pozos situados sobre las
conducciones en los cuales el agua fluctúa según cambios de presión, amortiguando los
golpes de ariete que se producen en las tuberías forzadas. Se entra más en detalle en
este tipo de fenómenos anómalos en el apartado 2.5.9.
Cabe comentar que las tomas de agua están protegidas, al igual que los desagües de
fondo que se trataban en el apartado 2.4.7, por rejillas, siendo la separación entre barras
tanto mayor para turbinas de mayor potencia.
Finalmente, el agua sale de la central por tubos de aspiración, seguidos de colectores
y de galerías de desagüe, como se puede apreciar en la Figura 9.
Figura 9. Sección por de una central hidroeléctrica (se aprecian sus conducciones). Ref: www.skycrapercity.com
2 Conceptos hidráulicos
2.5.9
28
Turbinas
El agua, originariamente retenida o almacenada y posteriormente encauzada y
controlada, y debido a la energía cinética desarrollada en su descenso, o a la energía de
presión, acciona directamente máquinas motrices que reciben el nombre de turbinas
hidráulicas, las cuales transforman la energía mecánica en energía eléctrica. Las
turbinas se pueden clasificar en dos tipos:
•
Turbinas de acción: aprovechan únicamente la velocidad del flujo de agua, la
cual incide en el mismo sentido de giro de los álabes (ver la siguiente figura).
Dentro de esta clase de turbinas tenemos las turbinas Pelton.
Figura 10. Incidencia del agua en una turbina Pelton
•
Turbinas de reacción: aprovechan la velocidad del flujo del agua, así como la
pérdida de presión que sufre dentro de la turbina. En este caso el agua no
incide frontalmente en los álabes. Dentro de esta clase de turbinas tenemos
las turbinas Kaplan y las Francis. Las turbinas Francis pueden ser de eje
horizontal, en las que el flujo de agua incide en la dirección radial, o de eje
vertical, en las que el flujo cambia su dirección radial a axial según inciden.
En las turbinas Kaplan el chorro incide en la dirección axial, tal y como si se
tratara de la hélice de un barco.
2 Conceptos hidráulicos
29
Figura 11. Turbina Kaplan
Merece la pena comentar que las turbinas hidráulicas, al ser máquinas complejas de
grandes dimensiones y estar bajo la acción de elevados esfuerzos mecánicos, no están
exentas de fenómenos anómalos. Estos fenómenos influyen negativamente en el
funcionamiento idóneo del grupo, si no se adoptan las medidas adecuadas para
eliminarlos o, por lo menos, reducirlos al máximo. Así tenemos los siguientes
fenómenos:
•
Cavitación: consiste en la formación, dentro de las masas líquidas, de
espacios huecos llenos de gas o vapor, producidos por una vaporación local
debido a acciones dinámicas. Se considera que las tensiones superficiales
producidas por estas acciones son del orden de 1000 atmósferas, valor lo
suficientemente elevado como para producir grietas, por fatiga del material,
en relativamente poco tiempo.
•
Golpe de ariete: al interrumpir con rapidez la corriente de un líquido que
circula con cierta velocidad que circula a través de un conducto, se producen
fuertes variaciones de presión sobre las paredes interiores de éste y del
elemento (p.e., una válvula) que corta el caudal suministrado, provocándose
impactos de consideración sobre todas las superficies expuestas a dichas
alteraciones. Como se comenta en el apartado 2.5.8, este fenómeno se
amortigua con las chimeneas de equilibrio.
3
Marco retributivo de la
producción hidroeléctrica
3 Marco retributivo de la producción hidroeléctrica
3
31
Marco retributivo de la producción hidroeléctrica
3.1
Introducción
En este capítulo se tratará en primer lugar el marco retributivo en el que se
encuentra inmerso el sector eléctrico (ver apartado 3.2) y en segundo lugar se ubicará la
posición que ocupa la producción hidroeléctrica dentro de dicho marco (ver apartados
3.3 y 3.5)
3.2
Ley del Sector Eléctrico (Ley 54/1997)
3.2.1
Introducción y antecedentes
La Ley 54/1997 (del Sector Eléctrico) introdujo un cambio regulatorio dentro del
sector eléctrico español: la introducción de la competencia. Por eso también es conocida
como la Ley de Liberalización del Sector.
Tuvo ciertos antecedentes con la Ley 40/1994 (Ley del Ordenamiento del Sector
Energético Nacional, LOSEN), que supuso un atisbo de apertura a la competencia, pero
es en 1996 con la firma del protocolo entre las empresas y el Ministerio correspondiente
cuando se planteó el desarrollo del mercado eléctrico que llegaría el 1 de enero de 1998.
España no es el único país donde se ha establecido la liberalización del Sector
Eléctrico. Otros países donde se habían establecido marcos regulatorios similares con
anterioridad eran Chile, Inglaterra, Argentina, algunos estados de EE.UU. y Noruega,
entre otros. A partir de las directivas europeas de 1996 y de 2003, los países de la Unión
Europea empiezan a desarrollar mercados internos de la energía de características
comunes.
3.2.2
Objetivos
Como ya se ha comentado, el sector eléctrico español opera de acuerdo con un
marco regulatorio liberalizado. Este marco se basa en la separación entre actividades
reguladas (distribución y transporte) y actividades no reguladas (generación y
comercialización), y en la existencia de competencia en las actividades de generación y
comercialización.
3 Marco retributivo de la producción hidroeléctrica
32
El marco retributivo que conlleva la liberalización del Sector Eléctrico persigue
como objetivo una mayor eficiencia en la producción, ya que las empresas compiten las
unas con las otras a la hora de comprar y vender energía eléctrica, lo cual desemboca
en la obtención de unos precios óptimos que al final benefician al consumidor. Estos
precios se suponen menores que los precios que existirían si se mantuviese la
retribución por costes estándares por tecnologías fijados administrativamente (por el
Gobierno), como sucedía anteriormente a la ley actual.
También se persigue otro objetivo fundamental en cualquier tipo de mercado: la
transparencia. Esto se consigue con la nueva regulación estructural, de tal modo que el
sistema eléctrico español está formado por el conjunto de empresas productoras,
transportistas, distribuidoras y comercializadoras de energía eléctrica, existiendo una
separación jurídica entre la generación y la distribución. Las empresas anteriormente
mencionadas
tienen
como
finalidad
fundamental
la
producción,
transporte,
distribución y venta de energía eléctrica, respectivamente. Se procede a comentar estas
actividades a continuación:
• Generación: la actividad de generación es aquélla destinada a generar energía
eléctrica (construir, operar y mantener las centrales de producción). Se divide en dos
grandes grupos: régimen ordinario y régimen especial.
• Transporte: la actividad de transporte es aquélla cuyo objeto es la transmisión de
energía eléctrica por la red interconectada, con el fin de suministrarla a los
distribuidores y a los consumidores finales, así como atender a los intercambios
internacionales. Esta actividad es llevada a cabo por Red Eléctrica Española (REE),
como operador del sistema y por las empresas transportistas (dueñas de las redes). Se
trata de una red mallada para asegurar su disponibilidad y la energía se transporta a
tensiones muy elevadas para reducir las pérdidas por intensidad debido a las grandes
distancias.
• Distribución: la actividad de distribución es aquélla que tiene por objeto la
transmisión de energía eléctrica desde las redes de transporte o desde otras redes de
distribución hasta los consumidores finales, así como vender energía a tarifa.
• Comercialización: la actividad de comercialización tiene como fin la venta de
energía eléctrica a los consumidores finales.
3 Marco retributivo de la producción hidroeléctrica
33
En la Figura 12 se observa un esquema sencillo del sistema eléctrico, en el que se
aprecian las distintas actividades que se han mencionado.
Figura 12. Sistema eléctrico
3.2.3
Mercado eléctrico
El caso es que, como ya se ha comentado, la ley 54/1997 surge en el contexto de una
tendencia mundial orientada a liberalizar el sector de la electricidad con el objetivo de
que sea lo más eficiente posible. Esta eficiencia se consigue si se maximiza el beneficio
social neto, el cual se entiende como:
B º SocialNeto = (U − PQ) + ∑ ( I − G )
i
Ecuación 18. Beneficio social neto
Donde el primer sumando representa la plusvalía de los consumidores, siendo U la
función utilidad (valor que tiene el bien adquirido desde el punto de vista del
consumidor) y PQ es lo que realmente le cuesta a los consumidores (precio que pagan
por cantidad), y el segundo sumando representa el beneficio de cada una de las
empresas i (entendido como la diferencia entre los ingresos y los gastos). Se supone
que en una competencia perfecta este beneficio es máximo porque el precio de
mercado es constante e igual al coste marginal.
El marco liberalizado propicia la existencia de un mercado mayorista en el que los
generadores venden su producción y los comercializadores y grandes consumidores
3 Marco retributivo de la producción hidroeléctrica
34
compran electricidad a través de transacciones bilaterales donde los intermediarios
ponen a compradores y vendedores en contacto, o directamente en el mercado pool o
en el mercado spot organizado. En estos dos últimos mercados, la casación del precio
que resulta de la intersección de las curvas de la oferta y la demanda eléctrica, la
realiza un operador (Operador del Mercado de la Electricidad, S.A., OMEL). Aparte de
la gestión de tipo económica del mercado diario e intradiario que hace OMEL, existe
un operador del sistema (REE) que se encarga de la gestión técnica, que asegura la
seguridad y la coordinación. Estos operadores independientes aseguran un
funcionamiento normal y adecuado del sistema.
3.2.4
Ley 17/2007
La nueva ley 17/2007, que se incorporó el 4 de julio de 2007, modifica la ley
54/1997. Es consecuencia, en gran medida, de la obligación de transposición en España
de la Directiva 2003/54, del Parlamento Europeo y del Consejo, sobre normas comunes
para el establecimiento del mercado interior de la electricidad, que deroga la anterior
Directiva 96/92 de la Comunidad Europea. Introduce cambios jurídicos en cuanto a los
pagos por capacidad (entendida como garantía de potencia).
3.3
Producción hidroeléctrica
Tal y como se comenta en el apartado 3.2.2, la generación eléctrica se divide en dos
grandes grupos: el régimen ordinario, que engloba gran parte de la generación
hidroeléctrica, la generación térmica convencional y la generación nuclear, y el régimen
especial.
La generación hidráulica (entendida como generación de grandes instalaciones) se
incluye dentro del régimen ordinario, quedando exentas las centrales minihidráulicas,
las cuales forman parte del régimen especial. El desarrollo del proyecto y de la
herramienta CARHI se centra en la generación hidráulica, por lo que sólo se
considerará el marco retributivo del régimen ordinario.
3.4
Marco retributivo del régimen ordinario
Queda establecido por la ley actual que toda la potencia disponible se ha de ofertar
bien por medio de contratos bilaterales, que incorporan las ventas a plazo en el
mercado, bien en el mercado diario e intradiario.
3 Marco retributivo de la producción hidroeléctrica
35
La potencia que no ha sido casada en el mercado, se pasa a ofertar para la
regulación secundaria, la regulación terciaria, los sistemas complementarios, la gestión
de desvíos y los pagos por capacidad. En este último las nuevas inversiones reciben
pagos por inversión y las inversiones ya existentes reciben pagos por disponibilidad.
3.5
Conclusiones
Las centrales que se gestionan en el modelo CARHI están retribuidas por régimen
ordinario y, por tanto, responden al marco retributivo comentado en el apartado 3.4.
Asimismo, las centrales del CARHI involucran embalses, turbinaciones y bombeos
de grandes dimensiones, en cuanto al tamaño, la producción hidroeléctrica y la
retribución económica. Por consiguiente, requieren de una optimización profunda (no
siendo así con las centrales fluyentes como lo son las minihidráulicas, las cuales no
atañen al proyecto como ya se ha comentado anteriormente). En el próximo capítulo se
tratará la gestión y optimización necesaria a la hora de llevar a cabo la producción
hidroeléctrica.
4
Sistemas hidroeléctricos
gestionados por Iberdrola
4 Sistemas hidroeléctricos gestionados por Iberdrola
4
4.1
37
Sistemas hidroeléctricos gestionados por Iberdrola
Introducción
El proyecto, como ya se ha comentado anteriormente, consiste en el modelado de las
características de embalses y centrales hidroeléctricas. Tiene, por tanto, una aplicación
genérica a cualquier embalse o central de cualquier compañía eléctrica.
No obstante, a la hora de comentar cuáles son las necesidades de gestión de la
energía y cómo se llega concretamente a la necesidad de la gestión del agua, nos
centraremos en Iberdrola, aunque la totalidad de este capítulo se puede aplicar a
cualquier otra compañía eléctrica, pues las necesidades de todas las compañías
eléctricas son muy similares.
En los próximos apartados comentaremos la gestión eléctrica y sus restricciones en
su conjunto (ver apartados 4.2 y 4.3), así como los activos de producción eléctrica (ver
apartado 4.4), para finalizar con la optimización y gestión concreta de los recursos
hidroeléctricos (ver apartado 4.5 y 4.6) y la posición que ocupa la herramienta
informática CARHI dentro de dicha gestión (ver apartado 4.7).
4.2
Restricciones
Como ya se comentó en el apartado anterior, la necesidad de satisfacer la demanda
eléctrica desde una perspectiva de la producción hidroeléctrica de régimen ordinario
conlleva una alta dificultad de optimización y planificación. En el diseño de esta
gestión hay que tener en cuenta dos factores muy importantes:
•
En cada instante de tiempo, la energía inyectada (generada) en la red debe
coincidir con la energía consumida. Por lo tanto, el sistema eléctrico es un
sistema dinámico de enormes dimensiones que permanentemente debe
mantener un equilibrio (reflejado en la frecuencia). En España se cumple
dicho equilibrio cuando la frecuencia se encuentra alrededor de los 50
Hertzios.
•
Normalmente las centrales de generación hidráulica están situadas en
localizaciones alejadas de los grandes consumos, ya que sólo se pueden
4 Sistemas hidroeléctricos gestionados por Iberdrola
38
construir en los ríos, y no en cualquier punto de los mismos. Por tanto, es
necesario instalar redes eléctricas que conecten dichas instalaciones.
Resultado de esto, la infraestructura de un sistema eléctrico de potencia es muy
compleja y está compuesta por un conjunto de instalaciones y sistemas de transporte y
distribución que abarcan desde las propias centrales generadoras, hasta las tomas que
en baja tensión alimentan directamente a los receptores de los usuarios. Esta
complejidad en el sistema se ha de tener en cuenta a la hora de realizar una
planificación y optimización.
Por último, también se encuentran otras restricciones como son el impacto
medioambiental y social, y la sostenibilidad.
4.3
Gestión de la energía
Básicamente, la dirección de gestión de la energía de una empresa eléctrica ha de
realizar las siguientes actividades:
•
Gestionar la compra de los combustibles necesarios para el funcionamiento
de los centros de producción eléctrica.
•
Gestionar y optimizar las ofertas de venta de energía en el mercado, según
unos márgenes determinados.
•
Informar a las instalaciones de las casaciones del mercado, para que estás
lleven a cabo el suministro eléctrico oportuno.
•
Actuar como operador global de los mercados mayoristas energéticos con
capacidades de trading, siendo la finalidad doble: proteger los activos
propios y su desarrollo a nivel europeo y mundial, y conseguir un nuevo
ámbito de negocio.
En todas las actividades anteriormente mencionadas, Iberdrola (y cualquier
compañía eléctrica) tiene como objetivo maximizar el margen de beneficio de sus
recursos y activos, siempre y cuando se respeten las restricciones que fueron
determinadas en el apartado 4.2. En el siguiente apartado, se procede a dar una breve
visión de los principales activos de Iberdrola.
4 Sistemas hidroeléctricos gestionados por Iberdrola
4.4
39
Sistemas de generación
Los activos de Iberdrola en España se pueden clasificar dentro de seis grandes
grupos:
•
La generación hidráulica: en la actualidad consta de 8842 MW de potencia
instalada (siendo 2349 MW de capacidad de bombeo) que supone el 43,5%
de la potencia total instalada en energía convencional por Iberdrola. Abarca
alrededor del 50% del total de potencia hidráulica instalada en España.
Figura 13. Depósito superior de la central La Muela
•
La generación térmica convencional: en la actualidad consta de 4135 MW de
potencia instalada (2888 MW de fuel – gas y 1247 MW de carbón) que
supone el 14% de la potencia total instalada en energía convencional por
Iberdrola. Abarca alrededor del 22,33% del total de potencia térmica
convencional instalada en España.
•
La generación nuclear: en la actualidad consta de 3344 MW de potencia
instalada que supone el 16,5% de la potencia total instalada en energía
convencional por Iberdrola. Abarca alrededor del 41,93% del total de
potencia nuclear instalada en España.
•
La generación de ciclos combinados: en la actualidad consta de 4800 MW de
potencia instalada (pasará a ser 5600 MW con la construcción Castellón IV)
que supone el 20% de la potencia total instalada en energía convencional por
4 Sistemas hidroeléctricos gestionados por Iberdrola
40
Iberdrola. Abarca alrededor del 33% del total de potencia en ciclos
combinados instalada en España.
•
La cogeneración: en la actualidad consta de 404 MW de potencia instalada.
•
La generación de energías renovables: en la actualidad consta de 4571 MW
de potencia instalada (4229 MW de energía eólica y 342 MW de centrales
minihidráulicas). Si se observa su potencia eólica instalada en todo el
mundo, asciende a 7704 MW, lo cual la hace líder mundial en el sector.
4.5
Optimización y gestión de sistemas hidroeléctricos
Se observa en el apartado anterior que una gran compañía eléctrica tiene activos de
muy diversas clases y de mucha potencia instalada. Como se comenta al final del
apartado 4.3, el objetivo de la compañía eléctrica es maximizar el beneficio, dentro de
todas las restricciones de tipo técnico, social y medio ambiental.
Para ello, lo mejor es abordar el problema dividiéndolo en sus partes, como se hace
con casi todos los problemas de tipo ingenieril – económico. Se va a realizar un estudio
centrado en la gestión hidroeléctrica, puesto que es el tema que atañe directamente al
proyecto y que desemboca en la necesidad de una herramienta que maneje las
características hidroeléctricas.
A continuación, se enumeran una serie de factores que hacen de la gestión
hidroeléctrica un problema de alta complejidad:
•
Predicción de la demanda
•
Predicción de las aportaciones de agua a los embalses
•
Modelado del sistema de generación
•
Modelado del mercado
•
Gestión de los factores de riesgo
•
Operación continua con muchas variables
A su vez, la modelización de la gestión hidroeléctrica se puede abordar desde
diversos ángulos:
4 Sistemas hidroeléctricos gestionados por Iberdrola
•
41
Según el plazo: muy corto (menos de un día), corto (de un día a una
semana), medio (desde varios meses a un año), largo (uno o varios
años) o muy largo (más de cinco años) plazo.
•
Según el sistema de ingresos: mercado (precios marginales, futuros,
etc.), contratos bilaterales o tarifas.
•
Según el modelado hidro – térmico: un embalse agregado y varias
unidades térmicas, un sistema de embalses y una unidad térmica
agregada o un sistema de embalses y un sistema de unidades
térmicas.
•
Según la naturaleza del modelo: modelos fundamentales (precisan de
una descripción del proceso) o modelos cuantitativos (el resultado es
un ajuste numérico de las variables, sin descripción del proceso).
•
Según la naturaleza de las variables: continuo o discreto, y
determinista o estocástico.
•
Según el tipo de modelo: equilibrio, optimización o simulación (ver
Figura 14).
•
Según la función objetivo y la técnica usada
Figura 14. Ejemplo de la simulación de la turbinación de un embalse
4 Sistemas hidroeléctricos gestionados por Iberdrola
42
Se observa que la descomposición del problema en sus partes conlleva que cada una
de ellas se pueda resolver de un modo diferente, cuadrando todos los resultados a
posteriori para poder extraer conclusiones y alcanzar los objetivos que se comentaban
en el apartado 4.3.
4.6
Características de los sistemas hidroeléctricos de Iberdrola
4.6.1
Introducción
Una vez se ha hecho un repaso a la gestión y optimización de los sistemas
hidroeléctricos, merece la pena dar una visión general de los sistemas hidroeléctricos
concretos de Iberdrola que aparecerán continuamente en la herramienta CARHI.
Los embalses y centrales de Iberdrola se pueden agrupar dentro de cuatro cuencas:
la cuenca del Sil, la cuenca del Duero, la cuenca del Tajo y la cuenca del
Mediterráneo/Norte (ver Figura 15)
Figura 15. Cuencas hidráulicas de Iberdrola
La herramienta CARHI está dividida en cinco partes según el río al que pertenecen
los embalses o centrales que se estudian: Duero, Tajo, Sil, Ebro y Júcar. A continuación,
se describen brevemente cada una de estas partes.
4 Sistemas hidroeléctricos gestionados por Iberdrola
4.6.2
43
Sil
Consta de 19 centrales hidroeléctricas con una potencia instalada total de 1273 MW.
Su gestión abarca el tramo del río Sil hasta San Pedro, y también los ríos Conso, Bibey,
Navea y Cenza.
Tiene embalses de muy diferentes características: hiperanuales, anuales, semanales
y diarios. Asimismo, tiene bombeos, canales, embalses que turbinan a un embalse, pero
vierten a otro, y embalses que pueden turbinar hacia dos embalses indistintamente.
Figura 16. Plano de la cuenca del Sil
4.6.3
Duero
Consta de 17 centrales hidroeléctricas con una potencia instalada total de 3320 MW.
Se trata del subsistema hidráulico más importante de Iberdrola. Un buen ejemplo que
ilustra esto es la presa de Almendra, que se trata del embalse más grande de España en
cuanto a reservas energéticas. Consta de un túnel de 15 km. de longitud que lleva agua
a la central de Villarino, donde se procede a turbinar (ver Figura 17).
4 Sistemas hidroeléctricos gestionados por Iberdrola
44
Figura 17. Embalse de la Almendra
En la utilización del Sistema Duero para el uso hidroeléctrico se pueden distinguir
cinco subsistemas: el Duero Alto, el Tera, el Esla, el Tormes y el Duero Bajo. Además
hay que tener en cuenta dos grandes embalses de cabecera gestionados por la
Confederación hidrográfica del Duero:
•
El embalse de Riaño, que se encuentra situado en la cabecera del río Esla,
está dedicado a riegos y regula la aportación natural al embalse de Ricobayo.
No está gestionado por Iberdrola.
•
El embalse de Santa Teresa, que se encuentra en el río Tormes, está aguas
arriba del embalse de Almendra. La central de Santa Teresa pertenece a
Iberdrola.
4.6.4
Tajo
La cuenca del Tajo se puede dividir en dos grupos:
•
El Tajo superior, que está formado por los embalses de Entrepeñas, Buendía
y Bolarque del que parte el canal del Trasvase Tajo-Segura, y cuyos embalses
y centrales no son gestionados por Iberdrola.
4 Sistemas hidroeléctricos gestionados por Iberdrola
•
45
El Tajo inferior, cuyas centrales hidráulicas explota Iberdrola. Consta de 9
centrales hidroeléctricas con una potencia instalada total de 2144 MW. Se
trata de centrales que reciben gran caudal.
Figura 18. Esquema topológico del Tajo inferior
Cabe mencionar una curiosidad que pueden hacer más “cercano” el estudio
posterior de las características hidráulicas:
•
La presa de Alcántara (José María Oriol) se tuvo que realizar en un punto
diferente del cauce porque en el lugar óptimo para su construcción hay un
puente romano de la época de Trajano (ver Figura 19).
4 Sistemas hidroeléctricos gestionados por Iberdrola
46
Figura 19. Puente romano de la presa de Alcántara
La presa tiene unos aliviaderos en los que se ha realizado un estudio hidrodinámico
para amortiguar las turbulencias antes grandes avenidas, de tal forma que no se dañe
el puente (ver Figura 20)
Figura 20. Presa de Alcántara ante grandes avenidas
4 Sistemas hidroeléctricos gestionados por Iberdrola
4.6.5
47
Sistemas del Ebro y Levante
Constan de una potencia instalada total de 1350 MW.
Dentro del sistema del Ebro, se pueden considerar tres grupos: el Ebro propiamente
dicho, Barázar y un conjunto de minicentrales que se encuentran en afluentes del Ebro
y en otros ríos que vierten al Mar Cantábrico. El río está regulado en su cabecera por el
embalse de Reinosa, el cual está gestionado por la Confederación Hidrográfica del
Ebro.
Dentro del sistema de Levante se pueden considerar cuatro grupos: Júcar
propiamente dicho, Segura, Mijares y Turia. Cabe mencionar el complejo de Cortes - La
Muela. La Muela es una central clásica de bombeo puro que eleva el agua a un
depósito superior de 4,5 km. de largo y superficie suficiente como para albergar todos
los campos de fútbol de primera y segunda división. Cortes es el embalse aguas abajo
(ver Figura 21).
Figura 21. Central de bombeo puro La Muela
Hemos podido observar en este apartado la variedad de embalses y centrales que
tiene Iberdrola. Por tanto, en el CARHI tendremos una amplia gama de características
diferentes según el tipo de embalse o central al que se refieren, por lo que se tendrán
que tratar de un modo diferente según el caso en el que nos encontremos.
4 Sistemas hidroeléctricos gestionados por Iberdrola
4.7
48
Conclusión
La herramienta informática que se desarrolla en este proyecto (Características
Hidroeléctricas, CARHI) se encuentra en el terreno base de donde parten todos los
escalones que constituyen el proceso de resolución del problema complejo
hidroeléctrico que ha sido tratado en el apartado 4.5. Es decir, se trata de una
herramienta básica y polivalente que puede servir, por ejemplo, de consulta a corto
plazo, de apoyo ante una duda en un modelo de simulación a medio plazo o de
programa de cálculo que trabaje en coordinación con un modelo de optimización a
largo plazo.
Asimismo, en el apartado 4.6 se ha realizado una breve descripción de los
subsistemas hidroeléctricos en su conjunto. Sin embargo, el CARHI se trata de una
herramienta que se centra en las características hidroeléctricas concretas de un único
embalse o de una única central, o a lo sumo de una central que tiene en cuenta a su
central paralela o al embalse al cual bombea o turbina. Describiremos cómo se ha
desarrollado y detallaremos su funcionamiento (basado en un enfoque aislado de un
embalse o una central) en el próximo capítulo.
5
Modelado de las características
hidroeléctricas (CARHI)
5 Modelado de las características hidroeléctricas
5
5.1
50
Modelado de las características hidroeléctricas
Introducción
En este capítulo se va a proceder a describir y detallar todos y cada uno de los pasos
que han sido necesarios para desarrollar la aplicación Características Hidroeléctricas
(CARHI), que modela, gestiona y calcula variables relacionadas con embalses y
centrales hidroeléctricas. Por tanto, éste constituye el núcleo de la memoria de proyecto
y, consecuentemente, ocupa gran parte de la misma. Asimismo, este capítulo muestra
que se han cumplido los requisitos que permiten considerar el trabajo como un
proyecto fin de carrera:
•
En primer lugar, se comprueba que el proyecto responde a una necesidad de
optimización y gestión de los recursos hidroeléctricos que era necesaria
resolver dentro del departamento Planificación y Ofertas de Iberdrola. Se
comprueba que efectivamente ha logrado su propósito. De hecho, la
herramienta CARHI tiene aplicación inmediata dentro de la empresa.
•
Asimismo, en capítulos anteriores se explican conceptos hidrodinámicos,
aspectos técnicos sobre las características de embalses y centrales
hidroeléctricas, aspectos relacionados con el marco retributivo de la
generación hidroeléctrica y aspectos relacionados con los recursos
hidroeléctricos de Iberdrola. No obstante, la complejidad es mayor, ya que
en este capítulo se observa que ha sido necesario programar en Fortran, en
Matlab y en Visual Basic. Asimismo, se comprueba que ha sido necesario
elaborar una herramienta de gestión y cálculo original y novedosa, pues si
bien supone una actualización al Modelo Hidráulico (MODHI), el entorno en
el que se desarrolla es completamente diferente, por lo que los códigos de
programación, las interfaces y la organización y control de datos dentro del
CARHI se han realizado partiendo de cero. Además, la herramienta CARHI
no sólo es capaz de proporcionar los mismos resultados que el MODHI, sino
que contiene varias ampliaciones respecto al mismo, haciendo de la
aplicación CARHI una herramienta completamente nueva y útil.
5 Modelado de las características hidroeléctricas
•
51
Por último, queda claro que la dedicación al proyecto fin de carrera ha
superado con creces las 300 horas de trabajo estimativas, ya que se ha
realizado en paralelo a una beca en prácticas de ocho meses en Iberdrola.
Antes de pasar a describir los pasos llevados a cabo en el modelado de la
herramienta es necesario remarcar que la aplicación CARHI sirve como modelo de
gestión y cálculo de características hidroeléctricas de embalses y centrales. Se podría
aplicar en cualquier compañía eléctrica, aunque el caso que se ha ocupado durante el
año ha sido la aplicación para los recursos hidroeléctricos de Iberdrola. De este modo,
en la memoria de proyecto ha sido necesario omitir los datos confidenciales, pero no
por ello el proyecto pierde su calidad académica. De hecho, no es necesario conocer la
información confidencial de los recursos hidroeléctricos de Iberdrola para describir el
proyecto y detallar el funcionamiento de la aplicación CARHI.
5.2
Modelo Hidráulico (MODHI)
5.2.1
Introducción
Hasta el momento el departamento de Gestión de la Energía, entre otras entidades
de Iberdrola, hacía uso del programa llamado Modelo Hidráulico (MODHI) como
herramienta fundamental de almacenamiento y cálculo de características de embalses
y centrales hidroeléctricas. El programa MODHI constituye, junto con otras
herramientas, la base en la que se apoya la optimización y la gestión del agua.
5.2.2
Descripción
El MODHI funciona en una versión del sistema operativo VMS. El acceso al mismo
es únicamente a través de un emulador de una consola de VAX - VMS, y la extracción
de datos así como el manejo de las funciones que contiene se tiene que hacer
fundamentalmente mediante programación en el lenguaje Fortran o por pantalla.
5 Modelado de las características hidroeléctricas
52
Figura 22. Menú principal del Modelo Hidráulico (MODHI)
Se trata de un sistema de archivos ISAM (Index Secuencial Access Memory): tanto si
se accede por programa en pantalla como por programación Fortran, se determina una
línea de varios códigos que hacen referencia a variables o instrucciones, de tal modo
que se accede a la línea de memoria directamente, sin necesidad de recorrer todo el
código cada vez que se quiera acceder a una posición de memoria. Por tanto, se
observa que el sistema operativo VMS y la programación en Fortran eran ventajosos en
tanto en cuanto a que la velocidad de cálculo es casi instantánea, se cuida al extremo
detalles como la capacidad de memoria o la longitud de las variables, y la forma de
organizar los datos y estructurar los códigos es rigurosa y óptima. Sin embargo, hoy en
día puede resultar tedioso el manejo de un programa en este entorno, puesto que en la
mayoría de las empresas la optimización y la planificación se realizan en entornos de
Excel y Matlab, usando lenguajes de programación como Visual Basic for Applications.
Es por ello que el objeto del proyecto es el desarrollo de la herramienta CARHI en un
entorno de Excel, apoyado mediante programación en Visual Basic y Matlab.
Por consiguiente, un paso indispensable para la realización de la aplicación CARHI
es la extracción de los datos y características hidroeléctricas que contiene el MODHI
(ver apartado 5.2.3), para que una vez controladas y organizadas se introduzcan en la
herramienta CARHI donde se implementaran subrutinas y funciones de Visual Basic
que permitan proporcionar y ampliar la información que contiene el MODHI.
5 Modelado de las características hidroeléctricas
5.2.3
53
Extracción de datos con Fortran
Como ya se ha comentado anteriormente, para extraer los datos del MODHI es
necesario llevar a cabo programación en Fortran. A continuación, se muestra un
diagrama (ver Figura 23) que indica los pasos necesarios que se han realizado para
proceder a la extracción de los datos:
Figura 23. Proceso de programación en Fortran para extraer datos del MODHI
Los archivos de extensión .for contienen el código en Fortran necesario para la
extracción de datos que, una vez compilados mediante archivos .com, se almacenan en
los archivos de extensión .obj. El código en los archivos .for a su vez hace referencia
mediante llamadas a unos archivos de extensión .car donde se ha escrito un programa
que contiene todos los códigos que hacen referencia tanto a las variables como a las
instrucciones del MODHI. Por último, los archivos de extensión .obj se convierten en
ejecutables que tienen una extensión .sal mediante el uso de librerías, haciendo un link
a una instrucción del programa MODHI.
En
concreto,
ha
sido
necesario
crear
dos
archivos
de
extensión
.car:
EMBALSES.CAR Y CENTRALES.CAR (ver anexos A.1 y A.2). En ellos se observa parte
de los códigos que hacen referencia a cada cuenca hidráulica, a cada embalse o central
en cuestión, y al número de embalses o centrales de cada cuenca. Desde los archivos
.for se realizarán llamadas a los archivos .car para obtener sus códigos.
Se ha procedido a realizar cuatro archivos de extensión .for: CARHI.FOR,
CARHICEN.FOR, CARHIRESTOS.FOR y CARHICENRESTOS.FOR (ver anexos A.3,
A.4, A.5 y A.6). A continuación se muestra una tabla que indica las distintas funciones
5 Modelado de las características hidroeléctricas
54
del MODHI que se han extraído mediante el código de programación de cada uno de
los archivos de extensión.for:
ARCHIVOS CON CÓDIGO FORTRAN
FUNCIONES QUE SE EXTRAEN
CARHI.FOR
COTA – VOLUMEN ÚTIL DE EMBALSE
CARHI.FOR
COTA – VOLUMEN TOTAL DE EMBALSE
CARHICEN.FOR
CAUDAL TOTAL – COTA AFTERBAY
CARHICEN.FOR
CAUDAL UNITARIO – PÉRDIDA DE CARGA
CARHICEN.FOR
SALTO NETO – POTENCIA UNITARIA MÁXIMA
CARHICEN.FOR
SALTO NETO – CAUDAL UNITARIO MÁXIMO
CARHICEN.FOR
CAUDAL UNITARIO – POTENCIA UNITARIA
CARHICEN.FOR
POTENCIA UNITARIA – CAUDAL UNITARIO
CARHICEN.FOR
SALTO BRUTO – POTENCIA DE BOMBEO
CARHICEN.FOR
SALTO BRUTO – CAUDAL DE BOMBEO
CARHIRESTOS.FOR
COTAS RANGO DE LAS FUNCIONES
EXTRAÍDAS POR CARHI.FOR
CARHICENRESTOS.FOR
NÚMERO DE GRUPOS, POTENCIAS MÁXIMAS,
COTA DE DESAGÜE Y COTAS DE EMBALSES
ASOCIADOS A LAS CENTRALES
Tabla 2. Funciones extraídas por los distintos códigos de Fortran
El MODHI proporciona información por dos vías. Los llamados datos fijos y los
llamados datos variables. Éstos se corresponden con cálculos que realiza el usuario
mientras que aquéllos se corresponden con información estática de características de
embalses y centrales, como son los coeficientes de las curvas, ciertos datos generales y
ciertos límites de aplicación. Todas las funciones extraídas con los archivos .for se
corresponden con los llamados datos fijos. Se almacenan en archivos de extensión .sal
que no se pueden incluir en la memoria de proyecto debido a la confidencialidad de los
datos, aunque en la Tabla 3 se describen las variables genéricas que se obtienen a partir
del MODHI así como las características que llevan asociadas. D existen unas
características variables proceden de los archivos generados de nombre CARHI.FOR y
CARHICEN.FOR. Por otro lado, existen unas características fijas obtenidas mediante
5 Modelado de las características hidroeléctricas
55
CARHIRESTOS.FOR y CARHICENRESTOS.FOR que se muestran en la Tabla 4 y en la
Tabla 5 respectivamente.
VARIABLES
CARACTERÍSTICAS ASOCIADAS
NCURVAS
Número de curvas existentes de la función
IREF
Indicativo de existencia de variable de referencia
ILIM
Indicativo de la existencia de límite de aplicación
IVAR
Número de variables independientes de la función
IGRA
Grado del polinomio
VREF
Valor de referencia para la curva (si existe)
VLIM
Valor límite máximo
VVAR
Variables no principales asociadas a cada curva
COEF
Coeficientes de cada una de las curvas
ISTAT
Status
Tabla 3. Variables y características asociadas en la extracción de datos con Fortran (archivos CARHI.FOR y
CARHICEN.FOR)
VARIABLES
CARACTERÍSTICAS ASOCIADAS
COTMINEX
Cota mínima extraordinaria
COTRGSUP
Cota de cambio de tramo
COTRGINF
Cota de cambio de tramo
COTMAXNOR
Cota máxima normal
COTMINNOR
Cota mínima normal
Tabla 4. Características generales extraídas mediante el archivo CARHIRESTOS.FOR de Fortran
5 Modelado de las características hidroeléctricas
56
VARIABLES
CARACTERÍSTICAS ASOCIADAS
NGGEN
Número de grupos de turbinación
NGBOM
Número de grupos de bombeo
COTADES
Cota de desagüe
COTMINEMBAA
Cota mínima del embalse aguas arriba
COTMAXEMBAA
Cota máxima del embalse aguas arriba
COTMINEMBAAB
Cota mínima del embalse aguas abajo
COTMAXEMBAAB
Cota máxima del embalse aguas abajo
Tabla 5. Características generales extraídas mediante el archivo CARHICENRESTOS.FOR de Fortran
Las rutinas de cálculo que el MODHI realiza para los llamados datos variables no se
han extraído, puesto que el CARHI se desarrolla en un entorno de Excel, por lo que
todas las rutinas y funciones necesarias para los procesos de cálculo han de ser
realizadas partiendo de cero para estar en concordancia con la programación en Visual
Basic.
Por último, merece la pena comentar el pseudocódigo de los archivos de extensión
.for para facilitar al lector de esta memoria la comprensión de los mismos. Se omitirá la
explicación de los fundamentos de la programación en Fortran, puesto que no es el
objeto del proyecto.
Pseudocódigo de los archivos .for
•
Declaración de variables y constantes necesarias para la realización de los
diferentes bucles
•
Declaración de variables necesarias para hacer llamadas a los archivos .car
•
Apertura de los archivos .car a los cuales se llamará desde los bucles del
código
•
Apertura de los archivos de salida .sal (.obj) donde se almacenarán los datos
extraídos
•
DO I = 1, Número de cuencas
5 Modelado de las características hidroeléctricas
57
DO J = 1, Número de embalses o centrales
o
DO K = 1, Número de funciones a extraer
9 Escritura (WRITE) de encabezados y tablas en archivo
.sal
9 Extracción
(CALL)
de
funciones
mediante
instrucciones del MODHI
o
5.2.4
CONTINUE
CONTINUE
•
CONTINUE
•
COMPROBACIÓN DE FIN DE CÓDIGO
•
END
Control de datos en Excel con VBA
Una vez se tiene toda la información necesaria en los archivos ejecutables de
extensión .sal, se pueden abrir archivos de tipo texto. No obstante, si los abrimos en un
formato tipo texto, no es posible organizarlos y filtrarlos como paso previo al control
analítico y gráfico que se pretende hacer en Matlab (ver apartado 5.3.2). Por ello, es
necesario en primer lugar gestionar la información mediante programación en Visual
Basic dentro de libros de Excel. Una vez se organizan los datos y se filtra el posible
ruido derivado de la programación en Fortran, se pasan las características a archivos
de extensión .mat, desde los cuales se puede acceder y realizar un control analítico y
gráfico de los mismos mediante programación en Matlab. Este proceso se muestra
esquemáticamente en la Figura 24.
5 Modelado de las características hidroeléctricas
58
Figura 24. Control de características extraídas del MODHI mediante programación en Visual Basic
Los archivos tipo texto no se incluyen en la memoria de proyecto, debido a su
carácter confidencial, pero a continuación se muestra, con ciertos datos omitidos, un
extracto de un solo embalse o central (de los 50 embalses y 55 centrales cuyas
características han sido extraídas) dentro de una única función (de las doce funciones
obtenidas con Fortran, ver Tabla 2) para justificar el control previo mediante VBA en
Excel:
SISTEMA: SISTEMA XXXXXXXXXXXX
**************************************************
FUNCIÓN
CENTRAL
GRADO
NCURVAS IREF ILIM IVAR ISTAT
----------------- ------ ---- ---- ---- ------------------------------------------------------J VREF(J)
VLIM(J)
VVAR(1,J)
VVAR(2,J)
COEF(1,J)
COEF(2,J)
COEF(3,J)
COEF(4,J)
COEF(5,J)
- -------------------------------------------------------------------XXXXXXXX
XXXXXXXX
3
8
F
F
2
0
1 0.000000E+00 0.999900E+04 0.270000E+02 0.000000E+00 0.143550E+01 0.235930E+00 0.688110E-03 -0.133020E-04 0.000000E+00
2 0.000000E+00 0.000000E+00 0.310000E+02 0.000000E+00 0.187140E+01 0.317160E+00 -0.842010E-03 0.469340E-05 0.000000E+00
3 0.000000E+00 0.000000E+00 0.350000E+02 0.000000E+00 0.212580E+01 0.357340E+00 -0.431480E-03 -0.136410E-05 0.000000E+00
4 0.000000E+00 0.000000E+00 0.390000E+02 0.000000E+00 0.239170E+01 0.400460E+00 -0.186610E-03 -0.542790E-05 0.000000E+00
5 0.000000E+00 0.000000E+00 0.430000E+02 0.000000E+00 0.265620E+01 0.442410E+00 0.237220E-03 -0.124270E-04 0.000000E+00
6 0.000000E+00 0.000000E+00 0.470000E+02 0.000000E+00 0.296960E+01 0.498470E+00 -0.403130E-03 -0.589660E-05 0.000000E+00
5 Modelado de las características hidroeléctricas
59
7 0.000000E+00 0.000000E+00 0.510000E+02 0.000000E+00 0.313510E+01 0.522130E+00 0.291570E-03 -0.141320E-04 0.000000E+00
8 0.000000E+00 0.000000E+00 0.550000E+02 0.000000E+00 0.340180E+01 0.568670E+00 -0.573840E-04 -0.983030E-05 0.000000E+00
9 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
10 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
11 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
12 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
13 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
14 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
15 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
16 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
17 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
18 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
19 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
20 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
21 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
22 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00
Se observa la gran magnitud de datos extraídos y la necesidad de ordenarlos y
filtrar el ruido asociado. Para ello, ha sido necesario automatizar el proceso mediante
programación en Visual Basic, puesto que de hacerlo uno a uno a mano no habría sido
posible cumplir los plazos de entrega del proyecto.
La programación en Visual Basic que organiza las características y elimina el ruido
asociado es análoga para las características de las funciones de embalses y para las
características de las funciones de centrales. Esto se debe a que, a pesar de que aquéllos
se extrajeron mediante CARHI.FOR y éstos se extrajeron mediante CARHICEN.FOR,
todos los archivos .sal asociados guardan una gran similitud.
Un caso ejemplo de una de las pocas diferencias que existen entre los códigos de
VBA es en que la función que relaciona la cota con el volumen total del embalse, la
variable NCURVAS (ver Tabla 3) no era correcta, por lo que no era posible valerse de
ella en la programación en VBA para eliminar todas las filas de coeficientes que
introducían ruido. Por tanto, se tuvo que incluir una subrutina especial para el caso de
5 Modelado de las características hidroeléctricas
60
esta función, que detecta las filas donde existe ruido mediante un recorrido de todas
las celdas, filtrando aquéllas que tenían valores nulos.
El caso es que en el anexo B sólo se incluyen los códigos genéricos para el control,
filtrado y organización de las características de embalses y centrales. En el anexo B.1 se
incluye el código con las subrutinas de nombre Macro(), en el cual se controlan los
datos y se filtra el ruido, y en el anexo B.2 se incluye el código con las subrutinas de
nombre Matlb(), en el cual se preparan y organizan los datos para introducirlos en
archivos de extensión .mat a los que se puede hacer referencia mediante programación
en Matlab.
5.3
Características hidroeléctricas (CARHI)
5.3.1
Introducción
En los capítulos anteriores se han descrito todos los pasos previos y necesarios al
desarrollo de la herramienta CARHI: estudio de la física del agua (capítulo 2), estudio
la gestión del agua dentro del marco eléctrico (capítulo 3) y, en concreto, dentro de
Iberdrola (capítulo 4), y extracción de todos los datos y características hidroeléctricas
posibles contenidos en el MODHI (capítulo 5.2).
En este capítulo se procederá a describir el desarrollo concreto de la herramienta
CARHI en concreto (ver apartado 5.3.3). No obstante, antes de empezar a describir el
CARHI, se va comentar el tratamiento de datos que se ha llevado a cabo en Matlab
desde un punto de vista analítico y gráfico (ver apartado 5.3.2).
5.3.2
Tratamiento de datos en Matlab
Este apartado no se ha incluido en el apartado 5.2 porque los resultados gráficos
obtenidos en Matlab se han transferido a formato .jpg y se han incluido dentro de unas
carpetas anexas al directorio donde se encuentra el CARHI, de tal modo que se puede
acceder a las gráficas de las distintas curvas de características hidroeléctricas mediante
botones de comando en Excel que llevan asociada programación en Visual Basic. Por
tanto, sus resultados gráficos afectan explícitamente al CARHI, siendo oportuno
considerar el tratamiento de datos en Matlab dentro del capítulo del apartado del
CARHI propiamente dicho (apartado 5.3).
5 Modelado de las características hidroeléctricas
61
En relación a la aplicación directa de gráficas de Matlab en Excel, se ha de notar que
no es bidireccional, sino unidireccional. Es decir, se pueden gestionar características
hidroeléctricas y realizar cálculos de variables en Excel mediante VBA, siendo la
relación entre la aplicación en el entorno de Excel y Visual Basic de tipo bidireccional.
Sin embargo, la relación entre la aplicación y el desarrollo gráfico obtenido en Matlab
es de tipo unidireccional, puesto que las gráficas transferidas a formato .jpg son
imágenes estáticas, y si se precisa modificarlas, será necesario acudir a Matlab y
cambiar el código de programación para así volver a generar nuevas imágenes. Esta
triple relación bidireccional (entre el CARHI y VBA) y unidireccional (entre el CARHI
y los resultados gráficos de Matlab) se describe en la Figura 25:
Figura 25. Relación entre Excel, Visual Basic y Matlab en la herramienta CARHI
Aparte de la creación de gráficas que se incluyen en la herramienta Excel, el
tratamiento llevado a cabo en Matlab ha servido no sólo para detectar y filtrar errores,
sino también para determinar límites de rango en las abscisas de las funciones en
cuestión. En muchas ocasiones se han establecido filtros que limitan los datos a valores
razonables desde el punto de vista físico de los embalses y centrales (ver apartado
5.3.2.4, entre otros). En otros casos, se ha tenido que acudir a literatura externa de
Iberdrola para poder suministrar ciertos límites completamente necesarios (ver
apartado 5.3.2.3, entre otros). Estos límites de rango son especialmente importantes
porque se incluyen en el CARHI como restricción para los cálculos.
A continuación se procede a describir las funciones que se han tratado analítica y
gráficamente en Matlab:
5 Modelado de las características hidroeléctricas
5.3.2.1
62
Volumen útil y volumen total en función de la cota del embalse
Se trata de funciones de 4º grado. Se ha procedido a dibujarlas superpuestas, de tal
modo que en el eje de las abscisas se tiene la cota en metros sobre el nivel del mar y en
el eje de las ordenadas se tiene tanto el volumen útil como el volumen total en hm3.
Como ya se estudió en el capítulo 2, la curva del volumen total ha de ser igual a la
curva de volumen útil más una constante (igual al volumen muerto). Por tanto, se tuvo
que tratar los datos modificando las variables sobre las que se construía la curva hasta
obtener gráficas que tuvieran la siguiente forma:
Figura 26. Curva que relaciona la cota con el volumen útil y el volumen total de un embalse
Se observa que efectivamente la curva de volumen total es paralela a la curva de
volumen útil por una constante que representa el volumen muerto. Cabe mencionar
que para el ejemplo de la Figura 26, en el rango de cotas menores de 1315 msnm la
curva de volumen total sigue un tramo mientras que para cotas mayores sigue otro
tramo (que por supuesto coincide en la abscisa de 1315 msnm tanto en el punto como
5 Modelado de las características hidroeléctricas
63
en su derivada primera). Esto se debe a que cuando se hizo el ajuste de la curva a partir
de datos de medida que se hubiera realizado en la cuenca en cuestión, se observó que
realizar el ajuste con una sóla curva no era muy preciso, por lo que se optó por realizar
dos tramos. No es una casualidad que la unión de ambos tramos coincida en la cota a
la cual el volumen útil es cero, pues a partir de ella es donde la curva de volumen total
ha de pasar a ser paralela por las razones anteriormente mencionadas. La cota donde el
volumen total es cero se corresponde con la variable COTRGSUP (ver Tabla 4). Se ha
de notar que no siempre la curva de volumen total está compuesta por dos tramos (no
fue necesario en los casos en los cuales el ajuste de los datos de medición mediante una
única curva fuera lo suficientemente preciso) y en tales casos la variable COTRGSUP
obtenida es cero. La variable COTRGINF (ver Tabla 4) tiene cabida sólo cuando se ha
procedido a realizar tres tramos para dibujar la curva de volumen total.
El caso es que tras realizar un estudio gráfico de las curvas, se determinó que las
funciones de 4º grado respondían a la siguiente ecuación:
Vol = a 0 + a1 × (Cota − Cota Re f ) + a 2 × (Cota − Cota Re f ) 2 + a3 × (Cota − Cota Re f ) 3 +
+ a 4 × (Cota − Cota Re f ) 4
[hm ]
3
Ecuación 19. Relación entre la cota y el volumen útil y total
Tras el estudio gráfico, se determinó analíticamente que el límite de aplicación
mínimo para la curva de volumen útil es la cota mínima extraordinaria (COTMINEX,
ver Tabla 3), mientras que para la curva de volumen total es la cota mínima normal
(COTMINNOR, ver Tabla 3). Esta diferencia en las los límites de aplicación mínimos se
justifica porque al hacer uso de ellas, el volumen útil y el volumen total
correspondientes con el límite mínimo son nulos (como debe ser).
Por otra parte, se ha de notar en la Ecuación 19 que la cota de referencia se usa a la
hora de calcular el volumen mediante los coeficientes de la curva, pero cuando dicha
curva se procesa gráficamente, los valores del eje de abscisas se corresponden con la
cota (sin restar la cota de referencia). Esto se puede observar en la instrucción plot del
código hecho en Matlab para dibujar la gráfica (ver anexo C.1). En cuanto al código en
Matlab del anexo C.1 merece la pena comentar que la curva de volumen total del
embalse de Valdecañas no se ajustaba como era necesario, por lo que se hizo un ajuste
5 Modelado de las características hidroeléctricas
64
nuevo con Matlab mediante una aproximación de cuarto grado, que se especifica a
continuación del código del anexo C.1.
Asimismo, se determinó en el tratamiento analítico considerar como límite superior
de la curva, a la hora de dibujarla, la cota máxima del embalse en cuestión, que se
extrajo del MODHI mediante el archivo CARHIRESTOS.FOR (ver Tabla 4), puesto que
en el MODHI no se proporcionaba el límite superior para estas curvas (VLIM era igual
a cero, ver Tabla 3).
5.3.2.2
Cota de desagüe en función del caudal turbinado y vertido total de la central,
la cota del embalse aguas abajo y el caudal turbinado por la central paralela
Se trata de funciones de tercer grado. El MODHI proporciona varias curvas para
distintas cotas de embalses aguas arriba y caudal turbinado por la central paralela (en
el caso de que aplique).
Tiene sentido que la cota afterbay dependa del caudal total, entendido como caudal
total de la central en cuestión (suma del caudal de todos los grupos que están
turbinando sumado al caudal vertido de la central y al caudal total de la central
paralela), y que también dependa de la cota del embalse aguas abajo, pues la cota de
desagüe es la cota a la salida de máquinas, por lo que está íntimamente relacionada con
la cota del embalse aguas abajo.
Por otro lado, en el análisis gráfico se ha observado que aquellas centrales cuyo
caudal turbinado por la central paralela es nulo en todos los casos, carecen de central
paralela, mientras que aquellas centrales que tengan ciertas curvas para caudal de
central paralela nulos y otras para un determinado caudal de central paralela, son
centrales que efectivamente tienen una central paralela asociada (en la que a veces se
turbina y otras veces no).
Las gráficas de este tipo de curvas han de responder al siguiente aspecto:
5 Modelado de las características hidroeléctricas
65
Figura 27. Curva que relaciona el caudal total con la cota de desagüe de la central
Asimismo, en el estudio gráfico en Matlab se ha observado que para un valor nulo
de abscisas (las curvas se dibujan desde un caudal igual a cero), el valor de ordenadas
para el que comienza la curva coincide con la cota del embalse aguas abajo y cuando
éste no aplique, el valor de ordenadas coincide con la cota de salida de máquinas de la
central en cuestión. Existen ciertos casos en los que se produce una peculiaridad al
respecto. Obsérvese la Figura 28:
5 Modelado de las características hidroeléctricas
66
Figura 28. Impacto del cuenco amortiguador en la curva que relaciona caudal turbinado y vertido con la cota afterbay
Se observa que en la leyenda se indica que la cota del embalse aguas abajo es 229
msnm en el caso de la curva verde. Sin embargo, esta curva comienza para la cota de
240 msnm. Esta aparente discrepancia se debe a la formación del cuenco amortiguador.
En la Figura 29 se observa la imagen de un cuenco amortiguador:
5 Modelado de las características hidroeléctricas
67
Figura 29. Cuenco amortiguador. Ref: www.skyscrapercity.com
Por último, cabe comentar el filtrado de rango que se ha realizado entre las líneas
105 y 121 del código en Matlab (ver anexo C.2). Se trata de un rango que filtra en
primer lugar aquellas curvas que tenían asociadas un VLIM (ver Tabla 3) no razonable
físicamente y en segundo lugar filtra aquellas curvas que, aún teniendo un
determinado VLIM, tuvieran un máximo matemático dentro de su rango, puesto que
no tiene sentido físico alguno que a más caudal total se tenga una menor cota afterbay.
5.3.2.3
Pérdida de carga en función del caudal turbinado por un grupo y del número
de grupos turbinando
Se trata de curvas de segundo grado. El MODHI nos proporciona varias curvas para
distintos números de grupos turbinando.
Tiene sentido que la pérdida de carga sea para el caudal turbinado unitario, y no
total, pues la pérdida de carga pertenece precisamente a las conducciones y a la turbina
de ese grupo en cuestión, a través de las cuales sólo discurre el caudal turbinado.
Asimismo, se considera la pérdida de carga como una característica de un sólo grupo,
aunque en cierta literatura se hace referencia a la pérdida de carga de una central,
entendida como la suma de las pérdidas de carga de sus diferentes grupos.
5 Modelado de las características hidroeléctricas
68
El hecho de que haya curvas que son para más de un grupo se debe a que se sigue
considerando el caudal turbinado unitario, pero éste da lugar a mayor pérdida de
carga en el caso de que los grupos compartan conducciones como se observa en la
Figura 30:
Figura 30. Relación entre el caudal unitario y la pérdida de carga en una central donde los grupos comparten
conductos
En el caso de que cada grupo tenga conducciones independientes, el hecho de tener
más de un grupo turbinando no añade a la pérdida de carga total de la central, estando
todas las curvas superpuestas, como se observa en la Figura 31:
5 Modelado de las características hidroeléctricas
69
Figura 31. Relación entre el caudal unitario y la pérdida de carga en una central donde los grupos no comparten
conductos
Se observa que en esta función, al igual que en la función que relaciona caudal total
y cota de desagüe, se han dibujado las gráficas comenzando en un valor de abscisas
nulo (para un caudal igual a cero). En cuanto al límite superior de abscisas, los valores
de VLIM (ver Tabla 3) proporcionados son erróneos. Por ello, fue necesario proceder a
la búsqueda de ellas en literatura de Iberdrola (Características de los aprovechamientos
hidroeléctricos) para introducirlos manualmente en el archivo .mat, al cual llama el
código de programación en Matlab. El código en cuestión no se ha proporcionado
como anexo, ya que no aporta información nueva respecto de otros códigos del
anexo C.
5.3.2.4
Caudal unitario en función de la potencia de generación unitaria y potencia de
generación unitaria en función del caudal unitario, para distintos saltos netos
Se trata de funciones de tercer grado. El MODHI nos proporciona varias curvas para
distintos saltos netos. Se ha decidido tratar ambas funciones dentro del mismo
apartado, ya que una función es inversa de la otra, por lo que el concepto y el estudio
5 Modelado de las características hidroeléctricas
70
es el mismo. Por tanto, en el anexo C sólo se incluye el código de control y filtrado de
Matlab de una función (ver anexo C.3).
Tiene sentido que haya curvas que relacionen caudal y potencia para un salto neto,
pues la energía que le llega a la turbina es proporcional al producto de la densidad (del
agua), la aceleración de la gravedad, el salto neto y el caudal, y la energía que sale es
proporcional a la potencia. Como densidad y aceleración de la gravedad son
constantes, las curvas relacionan únicamente las características variables.
El resultado gráfico de las curvas tiene el siguiente aspecto:
Figura 32. Curva que relaciona el caudal unitario y la potencia de generación unitaria
Se observa que a medida que el salto neto aumenta, también aumenta el valor límite
superior del caudal que admite el grupo. Tiene sentido físico según lo estudiado en el
capítulo 2. Asimismo, esta peculiaridad se tendrá en cuenta en los cálculos que
proporciona el CARHI, a la hora de interpolar mediante programación en Visual Basic.
De este modo, para el caso de la Figura 32, si se precisa conocer la potencia para un
m3
) y un salto neto de 54 m, se
caudal intermedio (por ejemplo, un caudal de 150
s
5 Modelado de las características hidroeléctricas
71
realizará una interpolación entre la curva para salto neto de 52 m y la curva de salto
neto de 56m. Sin embargo, si se precisa un cálculo para un salto neto de 52 m y un
caudal Q1 cercano al límite máximo superior, posiblemente la curva interpolada de 52
m tenga un límite superior Q2 inferior al caudal Q1, en cuyo caso se realizarán los
cálculos para Q2 (indicándoselo al usuario). El código de Visual Basic que realiza esta
interpolación se detalla en el apartado 5.3.3.2.
Acerca del código de Matlab que se incluye en el anexo C.3, merece la pena
comentar que entre las líneas 77 y 87 se ha realizado un filtrado de ordenadas
negativas, puesto que el MODHI no proporciona límite inferior de abscisas.
Asimismo, el MODHI tampoco incluye explícitamente límite superior de abscisas,
pero de forma implícita se puede obtener mediante las funciones del apartado 5.3.2.5.
En la línea 28 del código de Matlab se observa la instrucción “load CoefHnQMax”, que
precisamente carga los coeficientes de las mencionadas funciones para poder hacer uso
de ellos.
5.3.2.5
Potencia unitaria máxima y caudal unitario máximo en función del salto neto
Se trata de funciones de segundo grado que ajustan los límites máximos de abscisas,
como ya se ha comentado en el apartado 5.3.2.4. Igual que en dicho apartado, se ha
decidido tratar en la memoria ambas funciones a la vez, ya que una función es inversa
de la otra, por lo que el concepto y el estudio es el mismo. Por tanto, en el anexo C sólo
se incluye el código de control y filtrado de Matlab de la función que relaciona salto
neto con potencia máxima por grupo (ver anexo C.4)
El aspecto de estas funciones es el siguiente:
5 Modelado de las características hidroeléctricas
72
Figura 33. Función que relaciona el salto neto con la potencia máxima unitaria
Se puede apreciar cierta tendencia de aplanamiento hacia valores altos de abscisas.
En algunas centrales el aplanamiento es todavía más acentuado. Esto se debe a que,
lógicamente, a mayor salto neto, mayor es la potencia o el caudal máximo que permite
el grupo de la central. Sin embargo, llega un momento en el que la apertura del
distribuidor de la turbina ya no admite más, por lo que el alternador no dará más
potencia aunque se incremente el salto neto.
Los VLIM (ver Tabla 2) que proporciona el MODHI para esta función no
representan los límites máximos reales. Por tanto, se procedió a calcular el salto neto
máximo como el 99% del salto bruto máximo, siendo éste la diferencia entre la cota
máxima del embalse aguas arriba y la cota de desagüe de la central. En el caso del salto
neto mínimo, que también es necesario y que el MODHI no facilita, se procede
igualmente con el 99% del salto bruto mínimo, entendido como la diferencia entre la
cota mínima del embalse aguas arriba y la cota de desagüe de la central. Todos estos
valores de cotas proceden de las características extraídas con el archivo
CARHIRESTOS.FOR (ver Tabla 4), y el 99% se debe a que el rendimiento de un circuito
5 Modelado de las características hidroeléctricas
73
hidráulico ronda el 97 – 99% (es tanto menor cuanto mayor sea el caudal). A
continuación se muestra la ecuación con la que se ha aproximado el salto neto:
Salto Neto teórico = η circuito hidráulico × (Cota embalse aguas arriba − Cota afterbay )
[m]
Ecuación 20. Salto neto teórico
No obstante, el hecho de considerar un 99% puede resultar en ciertas ocasiones
impreciso. Asimismo, aún considerando que el 99% es una aproximación precisa, no
tiene por qué coincidir con ese cálculo teórico, ya que para caudales bajos se puede ver
afectados por fenómenos diversos (como la cavitación, ver capítulo 2). Otra razón que
puede desvirtuar ese cálculo teórico sería el caso de una central en la cual el embalse
aguas arriba fuera lo suficientemente pequeño en comparación con el embalse aguas
abajo. En este caso, el salto neto mínimo posiblemente tendría que ser mayor del salto
neto mínimo calculado teóricamente, pues en caso contrario sería físicamente
imposible
que
se
produjera
turbinación.
Además,
en
algunas
ocasiones
CARHIRESTOS. FOR proporcionó valores nulos de cota de desagüe.
Por todas las razones expuestas en el párrafo anterior, se procedió a reconsiderar las
cotas mínimas y máximas de los embalses aguas abajo, así como se realizaron filtros de
diferentes tipos: máximo matemático, ordenada positiva, y crecimiento continuo y
positivo. Los dos primeros filtros se pueden apreciar en el código de Matlab del
anexo C.4. El último filtro de crecimiento continuo y positivo se realizó en un libro de
Excel (su nombre es “SALTONETO-CAUDALLIM (F6).xls”, pero no se puede adjuntar
por razones de confidencialidad de datos). En algunos casos donde ya no era posible
resolverlo mediante filtros, se acudió a la literatura de Iberdrola (Características de los
aprovechamientos hidroeléctricos).
5.3.2.6
Potencia de bombeo y caudal de bombeo en función del salto bruto y del
número de grupos
Se trata de funciones de tercer grado. El MODHI proporciona curvas para diferentes
saltos brutos.
Se trata del concepto análogo al apartado 5.3.2.5, pero en relación al bombeo, no a la
turbinación. Es decir, se trata del ajuste de los puntos de las funciones que relacionan
5 Modelado de las características hidroeléctricas
74
caudal de bombeo con potencia de bombeo. El código de Matlab es análogo, por lo que
no es necesario incluirlo en el anexo de la memoria.
Cabe comentar que, a diferencia de las funciones del apartado 5.3.2.5, se tienen
cortes según el número de grupos que están bombeando. Esto tiene sentido, pues el
bombeo tiene la limitación de que al poner a trabajar varios grupos, el salto bruto crece
tanto que puede llegar a imposibilitar que el bombeo pueda tener lugar. Debido a este
comportamiento físico, que ya se mencionó en el apartado 2.5.3, los grupos de bombeo
no son independientes los unos de los otros, por lo que es necesario incluir esa
dependencia en las funciones.
5.3.3
5.3.3.1
Desarrollo de la herramienta CARHI
Organización de la herramienta
En este apartado se presenta cómo se han organizado los datos y las características
que contiene la herramienta CARHI. Esta organización se expone enfocada desde el
punto de vista de su implantación informática por medio de programación en Visual
Basic for Applications (VBA). Se ha utilizado la orientación por medio de variables de
tipo estructura, en un esfuerzo por llegar a un algoritmo general que pueda ser usado
para representar cualquier embalse o central hidroeléctrica. De este modo, la transición
entre embalses y centrales se basa únicamente en la lectura de los datos y
características que correspondan, siendo el código de programación el mismo para
cada embalse y para cada central.
En el código de programación, el embalse o la central tienen asociados una
estructura (Emb y Ctr, respectivamente) y están representados por una colección de
elementos que pertenecen a la estructura. Dichos elementos pertenecen a
subestructuras a su vez, que reciben el nombre de Gral o Fc, según contengan
características generales y de explotación o coeficientes y rangos de las funciones,
respectivamente. En el anexo D.1 se encuentra el contenido del módulo del editor de
VBA donde se han realizado las declaraciones descritas.
Los elementos de carácter general (Gral) son almacenados en la estructura y sólo es
necesario usarlos una vez: cuando se carga un embalse o una central. Sin embargo, los
elementos de tipo Fc se usan cuando se carga el embalse o central, pero también se
usan posteriormente a la hora de realizar cálculos.
5 Modelado de las características hidroeléctricas
75
Debido a que siempre hay el mismo número de características generales, la parte del
código de VBA que carga esos datos es simple (ver anexo D.4). Sin embargo, en el caso
de los elementos de tipo Fc es necesario cargar los elementos mediante un bucle while
anidado dentro de un bucle for (ver anexo D.4).
A continuación se muestran unas tablas (ver Tabla 6, Tabla 7 y Tabla 8) donde se
encuentra la localización de las características generales y de explotación en la
herramienta:
Características generales
Celda que contiene el campo
Cota mínima de explotación normal
Cells(29,3)
Cota mínima de explotación extraordinaria
Cells(30,3)
Cota máxima de explotación normal
Cells(31,3)
Cota máxima de explotación extraordinaria
Cells(32,3)
Cota mínima para garantía de riegos
Cells(33,3)
Cota máxima para resguardo de avenidas
Cells(34,3)
Volumen total máximo
Cells(29,5)
Volumen útil máximo
Cells(30,5)
Tabla 6. Características de explotación de los embalses del CARHI
Cabe mencionar que los campos de cotas de garantía de riegos y de resguardo de
avenidas han de tener cabida para 12 ó 24 datos, según se tomen puntos a final de mes
o cada 15 días.
5 Modelado de las características hidroeléctricas
76
Características generales
Celda que contiene el campo
Comunidad Autónoma
Cells(12,2)
Provincia
Cells(13,2)
Municipio
Cells(14,2)
Cuenca hidrográfica
Cells(15,2)
Río
Cells(16,2)
Superficie
Cells(12,4)
Aportación media anual
Cells(13,4)
Caudal medio
Cells(14,4)
Precipitación media anual
Cells(15,4)
Desde los que turbina
Cells(12,6)
Hacia los que turbina
Cells(13,6)
Desde los que bombea
Cells(14,6)
Hacia los que bombea
Cells(15,6)
Tipo de central
Cells(24,2)
Número de grupos de generación
Cells(25,2)
Número de grupos de bombeo
Cells(26,2)
Tipo de turbinas
Cells(27,2)
Potencia instalada
Cells(28,2)
Cota de desagüe a plena carga
Cells(29,2)
Potencia máxima total
Cells(24,4)
Potencia máxima unitaria
Cells(25,4)
Caudal máximo
Cells(26,4)
Caudal máximo unitario
Cells(27,4)
Potencia máxima total de bombeo
Cells(24,6)
Potencia unitaria de bombeo
Cells(25,6)
Caudal máximo de bombeo
Cells(26,6)
Caudal unitario de bombeo
Cells(27,6)
Tabla 7. Características generales y de explotación de las centrales del CARHI
5 Modelado de las características hidroeléctricas
77
Características generales
Celda que contiene el campo
Comunidad Autónoma
Cells(11,2)
Provincia
Cells(12,2)
Municipio
Cells(13,2)
Cuenca hidrográfica
Cells(14,2)
Río
Cells(15,2)
Superficie
Cells(11,4)
Aportación media anual
Cells(12,4)
Caudal medio
Cells(13,4)
Precipitación media anual
Cells(14,4)
Máxima superficie inundada
Cells(11,6)
Volumen de embalse normal
Cells(12,6)
Longitud
Cells(13,6)
Principales
Cells(11,8)
Asociadas
Cells(12,8)
Trasvase
Cells(13,8)
Tipo de presa
Cells(20,2)
Altura sobre cimientos
Cells(21,2)
Longitud de coronación
Cells(22,2)
Número de compuertas
Cells(23,2)
Número de aliviaderos superiores
Cells(20,4)
Cota máxima de aliviaderos superiores
Cells(21,4)
Número de desagües de fondo
Cells(22,4)
Caudal máximo de desagües de fondo
Cells(23,4)
Riegos y abastecimientos
Cells(20,6)
Límites de producción
Cells(21,6)
Límites de evacuación
Cells(22,6)
Aforos relacionados
Cells(23,6)
Tabla 8. Características generales de los embalses del CARHI
5 Modelado de las características hidroeléctricas
5.3.3.2
78
Descripción del algoritmo
El algoritmo de la herramienta CARHI responde al esquema de la Figura 34:
Figura 34. Algoritmo de la herramienta CARHI
La descripción es la que sigue:
Siempre que se abre a la herramienta CARHI, se accede a la hoja que contiene el
menú principal. Esto se produce porque en el objeto ThisWorkbook se encuentra la
siguiente instrucción:
Private Sub Workbook_Open()
Sheets("Menú principal").Activate
End Sub
Desde el menú principal se puede acceder directamente a la hoja donde se cargan
las características del embalse o de la central, o se puede acceder a una hoja con
información de una cuenca, desde la cual a su vez se puede acceder a la hoja con las
características del embalse o de la central.
Se observa en la Figura 34 que existe una conexión con un conjunto de hojas (bajo el
nombre de Características de embalses o Características de centrales) entre la selección
5 Modelado de las características hidroeléctricas
79
de un embalse o central y la carga de sus características. Esta conexión representa la
ejecución de los códigos de búsqueda de embalse o central (ver anexo D.2), el llenado
de las estructuras con las características del embalse o la central (ver anexo D.3) y la
carga de las mismas en la hoja correspondiente al embalse o central (ver anexo D.4).
Cada uno de estos códigos se encuentra ubicado en un módulo diferente del Editor de
Visual Basic.
Existen dos razones por las que se cargan las características cada vez que se llama a
un embalse o una central:
•
Organización óptima y dinamismo de las bases de datos: los datos se cargan
de otras hojas que hacen las veces de base de datos. Hay una hoja que
contiene todos los datos de los elementos de VBA de tipo Gral (“Base de
datos embalse” y “Base de datos central”), y una hoja por cada función
existente (“F1”,…, “F10), a partir de las cuales se accede a las características
de los elementos de VBA de tipo Fc. El caso es que a la hora de modificar las
características de un embalse o central, basta con acceder a la base de datos
en cuestión y cambiar lo necesario de forma rápida y ordenada. Si hubiera
un libro por cada embalse o central, habría que ir al libro específico para
realizar el cambio y esto podría acabar generando errores porque no se
trataría de proceso tan sistemático ni ordenado. Asimismo, el hecho de
disponer de las características en una base de datos hace posible que siempre
que se introduzca o se modifique una variable, se puedan actualizar los
nombres de los distintos rangos, necesarios para las interfaces de VBA que se
usan en la herramienta (ver apartado 5.3.3.4).
•
Eficiencia y ahorro de espacio de memoria a la hora de programar en VBA: si
hubiera un libro por cada embalse o central, habría que repetir las mismas
instrucciones de código de Visual Basic para cada uno de ellos, lo cual
ocuparía mucho más espacio y sería en cierto modo ineficiente.
Por otro lado, se observa en la Figura 34 que la conexión existente con las
características de embalses y centrales al pasar del menú principal o de la hoja de la
cuenca a la hoja del embalse o central es bidireccional. Esta bidireccionalidad
representa la posibilidad de cálculo que tiene la herramienta CARHI. Es decir, una vez
cargadas las características de los elementos de la estructura, se puede volver a acudir a
5 Modelado de las características hidroeléctricas
80
ésta tantas veces como se quiera para realizar cálculos sobre condiciones de
funcionamiento introducidas por el usuario. Por ello, la declaración de las variables de
tipo estructura están declaradas como Public (ver anexo D.1).
Recapitulando, la aplicación CARHI no sólo actúa como mera base de datos que
carga características de embalses y centrales en las hojas “Datos de embalse” y “Datos
de central”, sino que también sirve como herramienta de cálculo de funciones. En la
Figura 35 se muestra un esquema explicativo del proceso que realiza el algoritmo
mediante programación en Visual Basic:
Figura 35 . Procesamiento del algoritmo
En la Figura 36 se muestran las diversas funciones disponibles, así como un
esquema general de las posibilidades que existen en las mencionadas hojas de “Datos
de embalse” y “Datos de central”:
Figura 36. Procedimientos de las hojas de embalses y centrales de CARHI
5 Modelado de las características hidroeléctricas
81
El desarrollo de estas funciones se realiza mediante códigos de Visual Basic, de tal
modo que cada función lleva asociada una subrutina concreta. El pseudocódigo de
todas las funciones tiene la siguiente estructura:
Pseudocódigo de las subrutinas de cálculo de funciones
•
Declaración de variables y constantes necesarias para la realización de los
diferentes bucles
•
Búsqueda y llenado de las variables de tipo estructura con los elementos
necesarios para el cálculo
•
Filtrado de las condiciones de funcionamiento introducidas por el usuario,
comprobando que cumplen los rangos de aplicación previamente cargados
•
Realización de los cálculos por medio de instrucciones Call a subrutinas de
cálculo que se encuentran en otro módulo del editor de Visual Basic y que
comparten más de una función
•
Carga del resultado y de comentarios anexos en la hoja del embalse o central
Los códigos de las subrutinas se encuentran en detalle en los anexos D.6 y D.7. A su
vez, como se ha comentado en el pseudocódigo, las subrutinas llaman a otras
subrutinas de cálculo polinómico o de realización de interpolaciones simple y dobles,
que comparten varias funciones a la vez. Sus códigos se encuentran en los anexos D.7 y
D.8.
Merece la pena comentar que la función que requiere de interpolación doble
(Private Sub CotAfterb) es la función que relaciona la cota afterbay con el caudal total,
la cota del embalse aguas abajo y el caudal turbinado por la central paralela.
Afortunadamente, los valores proporcionados por el MODHI de cota del embalse
aguas abajo y caudal turbinado por la central paralela permiten que la interpolación
doble no sea excesivamente complicada.
La razón por la que no se trata de una interpolación excesivamente complicada es
porque el punto doble a interpolar siempre se encuentra encuadrado por otros cuatro
puntos conocidos. Es decir, cada curva caudal total – cota afterbay viene definida por
un par de valores: (Cota de embalse aguas abajo, Caudal turbinado por la central
5 Modelado de las características hidroeléctricas
82
paralela) = (Caab,Qcp). Estos valores guardan una relación, de tal modo que existen N
curvas para un Caab constante y N Qcp distintos, y en caso de existir otras curvas para
otros valores de Caab, necesariamente serán N curvas y necesariamente los N Qcp
asociados coincidirán con los primeros. De este modo, siempre resulta una
interpolación doble representada en la Figura 37, quedando el punto (Caab, Qcp)
buscado encuadrado dentro de otros cuatro puntos:
Figura 37. Interpolación doble
Donde CaabA = CaabB, CaabC = CaabC, QcpA = QcpD y QcpB = QcpC.
Una vez hallados los cuatro puntos que encuadran al punto buscado (mediante la
subrutina Sub BuscHorqDoble) y se ha determinado la cota afterbay que llevan
asociadas
para
el
caudal
total
dado
(mediante
la
subrutina
Sub
ResultadoFcPolinomDoble), la interpolación para la cota afterbay buscada responde a
la Ecuación 21:
Cota afterbay = (1 - Peso1) * (1 - Peso2) * Cota afterbay A + (1 - Peso1) * Peso2 * Cota
afterbay B + Peso1 * Peso2 * Cota afterbay C + Peso1 * (1 - Peso2) * Cota afterbay D
Ecuación 21. Interpolación doble
Siendo los pesos establecidos los siguientes:
Peso1 = (Caab - CaabA) / (CaabC - CaabA)
5 Modelado de las características hidroeléctricas
83
Peso2 = (Qcp - QcpA) / (QcpC - QcpA)
Ecuación 22. Ecuaciones de pesos de la interpolación doble
Por último, cabe comentar que la herramienta CARHI carga las gráficas creadas por
Matlab, como ya se indicó en el apartado 5.3.2. Esto lo realiza mediante un código de
carga de imágenes que busca las figuras del embalse o central en concreto en carpetas
que se encuentran en el mismo directorio. Asimismo, siempre que se abandona la hoja
donde se cargan las gráficas, el botón de comando lleva asociada una subrutina de
VBA que las borra (gracias a que previamente se les ha dotado de un nombre). De este
modo, no se sobrecarga la capacidad de memoria de la herramienta. Estos códigos se
encuentran en el anexo D.11.
5.3.3.3
Cálculo de variables para unas condiciones de funcionamiento dadas
Este apartado se podría haber incluido en el apartado 5.3.3.2, pero se ha
diferenciado del resto de los códigos de programación en Visual Basic por tratarse de
un código que aúna los códigos de varias funciones a la vez, resultando ser el más
complejo desde el punto de vista teórico y de programación.
La herramienta CARHI proporciona una serie de variables para unas condiciones de
funcionamiento dadas. Las variables que proporciona provienen de las condiciones de
funcionamiento que introduce el usuario junto con el valor del caudal turbinado por
grupo correspondiente a dichas condiciones de funcionamiento. Este valor de caudal se
obtiene mediante una iteración que encuentra dicho caudal dentro de un error de
diferencia entre la potencia real y la potencia resultante de la iteración. Este error se
encuentra contemplado en la condición de salida del bucle while del anexo D.9.
Se puede observar en el código que dicho error es la potencia máxima de la central
en cuestión dividida entre un valor de ajuste. De este modo, el error siempre es
proporcional al orden de magnitud de la central, pues es función de la potencia
máxima de la misma.
No obstante, se puede dar el caso de que el error sea demasiado pequeño, por lo que
la iteración no convergería nunca. Éste sería el caso de una iteración en la que, pasados
unos cuantos ciclos, la potencia resultante se acerca mucho a la potencia real, por lo
que en cada ciclo de la iteración pasa a valer un valor P1 un poco mayor que la
5 Modelado de las características hidroeléctricas
84
potencia real (ya que el caudal Q1 del ciclo es el caudal anterior más el caudal máximo
entre el valor de ajuste), en el siguiente ciclo vale un valor P2 un poco menor que la
potencia real (ya que el caudal Q2 del ciclo es el caudal anterior menos el caudal
máximo entre el valor de ajuste), y así sucesivamente. Es decir, se mantendría
“vibrando” alrededor de la potencia real porque siempre estaría fuera del rango
marcado por la potencia más/menos el error permitido. Para solucionar este posible
comportamiento, se ha generado la variable PAntigPar, que almacena el valor de la
potencia cada dos ciclos (de ahí que se encuentre dentro de una condición if donde sólo
se entra en los ciclos pares). Cuando PantigPar coincide con la potencia resultante del
ciclo par en cuestión, se sale del bucle while, ya que se trata del inicio de lo que sería
una vibración no convergente alrededor de las condiciones de salida. El valor de
caudal que se proporciona en este caso es una media ponderada entre el caudal Q1 y el
caudal Q2 que se mencionan anteriormente. La media ponderada se hace entre las
variables QAntig y CopiaQAntig (ver código del anexo D.9), siendo QAntig el caudal
del ciclo par en el que se encuentra la iteración y CopiaQAntig el caudal del ciclo impar
inmediatamente anterior. Los pesos son las variables PesoPar y PesoImpar, y se han
obtenido tipificando el desvío de PAntigPar y PAntigImpar respecto de la variable
Potencia que introduce el usuario (ver el código del anexo D.9).
En el caso de que la iteración no converja, por razones relacionadas con variables
fuera de rango, se sale de ella pasada un número máximo de iteraciones, que está
contemplado bajo la variable NvueltasMax. En este caso, la herramienta CARHI
proporcionará un mensaje de “Fuera de rango” al usuario.
En la Figura 38 se describe el proceso iterativo descrito y las funciones en las que se
basa:
5 Modelado de las características hidroeléctricas
85
Figura 38. Iteración para unas condiciones de funcionamiento de una central
Cabe mencionar que el caudal inicial del que se parte para realizar la iteración es el
caudal resultante de la función que obtiene caudales unitarios para una potencia
unitaria y un salto neto (ver apartado 5.3.2.4), siendo la potencia unitaria la que ha
introducido el usuario como condición de funcionamiento. En un principio se
consideró tomar como salto neto el 99% de la diferencia entre la cota del embalse y la
cota del embalse aguas abajo, ambos datos provenientes de las condiciones de
funcionamiento que introduce el usuario. Sin embargo, resulta más conveniente
considerar la primera aproximación de salto neto como la media aritmética de los
límites de rango del salto neto para la central en cuestión. Este procedimiento se
encuentra en detalle en la subrutina SubItQInic. Esta subrutina, y el resto de subrutinas
correspondientes con las enumeradas en la Figura 38, se incluyen en el anexo D.10.
5.3.3.4
Desarrollo de interfaces
Como ya se ha comentado a lo largo de la memoria de proyecto, la programación en
Visual Basic for Applications no sólo permite el desarrollo de cálculos y la gestión de
5 Modelado de las características hidroeléctricas
86
las características de embalses y centrales dentro del CARHI, sino que también permite
el desarrollo de interfaces que permitan el uso de la herramienta al usuario.
Las interfaces son las siguientes:
Menús desplegables: se encuentran en el menú principal y en las hojas de cuencas.
Contienen los datos de los embalses o centrales que están bajo nombres de rangos
determinados. Estos nombres de rangos son a su vez actualizados por medio de otras
interfaces (botones de comando en las hojas “Datos generales de embalses” y “Datos
generales de centrales”).
Botones de comando: se encuentran a lo largo de las hojas de la herramienta
CARHI. Sus funciones son diversas: la carga de un embalse o central, el retorno al
menú principal, la impresión de datos, la realización de cálculos, etc.
Figura 39. Menús desplegables y botones de comando del CARHI
Botones de selección: facilitan la búsqueda de especificaciones de la hoja cuando se
manejan muchos datos y hay muchas filas ocupadas. Se encuentran tanto en la hoja del
embalse o de la central como en la hoja donde se cargan las figuras.
Figura 40. Botones de selección del CARHI
5 Modelado de las características hidroeléctricas
87
Botones de mensaje: informan al usuario acerca de una característica introducida
que está fuera de rango.
Figura 41. Mensaje de aviso en la herramienta CARHI
5.3.3.5
Uso de la interfaz
A lo largo del apartado 5.3.3 se ha comentado el desarrollo de la aplicación CARHI
desde el punto de vista de su implantación informática en Visual Basic, en tanto en
cuanto a la organización de los datos que resulta, los procesos que lleva a cabo el
algoritmo y el desarrollo de interfaces. Se considera oportuno finalizar este apartado
con una breve descripción de la interfaz CARHI.xls que sirva a modo de manual del
usuario de la herramienta.
El libro CARHI.xls consta de 23 hojas, 10 de las cuales constituyen la interfaz a la
que tiene acceso el usuario, y otras 13 que contienen todos los datos generales y
características de embalses y centrales.
Las hojas a las que tiene acceso el usuario son las siguientes:
•
Hoja “Menú principal”, a la cual se accede siempre que se abre la
herramienta, como se comenta en el apartado 5.3.3.2. Desde esta hoja se
puede acceder a un sistema en concreto (Duero, Ebro, Júcar, Sil o Tajo) o se
puede acceder directamente a un embalse o a una central.
•
Hojas “Duero”, “Ebro”, “Júcar”, “Sil” y “Tajo”, a las cuales se puede acceder
desde la hoja “Menú Principal”. En estas hojas hay información general y
5 Modelado de las características hidroeléctricas
88
gráfica del sistema en concreto, y se puede acceder a un embalse o a una
central (del sistema).
•
Hojas “Datos embalse” y “Datos central”, a las cuales se puede acceder bien
desde la hoja “Menú principal”, bien desde la hoja del sistema en el que se
encuentra el embalse o la central en concreto. En estas hojas hay
características generales y de explotación, coeficientes y rangos de las
funciones de explotación e interfaces que permiten realizar cálculos.
•
Hojas “Gráficas embalse” y “Gráficas central”, a las cuales se puede acceder
desde las hojas “Datos embalse” y “Datos central”, respectivamente. En estas
hojas se cargan las gráficas del embalse o de la central en cuestión. Se trata
de las gráficas que se han obtenido mediante programación en Matlab, como
se comenta en el apartado 5.3.2.
Las hojas que contienen todos los datos generales y características de embalses y
centrales son las siguientes:
•
Hojas “Base de datos embalses” y “Base de datos centrales”. Contienen las
características generales y de explotación que se cargan mediante
programación en VBA en las hojas “Datos embalse” y “Datos central”.
Siempre que el propietario de la herramienta CARHI introduzca cambios en
algún embalse o central, actualizará los rangos de los embalses o las
centrales mediante el botón de comando “Actualiza rangos” que se
encuentra tanto en la hoja “Base de datos embalses” y “Base de datos
centrales”. Este botón lleva asociada una subrutina (ver anexo D.12) que
actualiza los rangos de celda de embalses y centrales, necesario para el buen
funcionamiento de la aplicación, puesto que los menús desplegables de la
hoja “Menú principal” y de las hojas de los sistemas hacen referencia a ellos.
•
Hojas “F1”, “Inversa F1”, “F2”, “F3”, “F4”, “F5”, “F6”, “F7”, “F8”, “F9” y
“F10”. Contienen los coeficientes y rangos de las funciones de explotación
que se cargan en las hojas “Datos embalse” y “Datos central”, y que se
graban dentro de las estructuras de programación en VBA para poder llevar
a cabo cálculos en las mencionadas hojas “Datos embalse” y “Datos central”.
5 Modelado de las características hidroeléctricas
5.3.4
5.3.4.1
89
Ampliaciones que añade la herramienta CARHI
Información sobre rangos
Tal y como se comentaba en el apartado 5.3.2, uno de los valores añadido que aporta
el control y tratamiento de datos realizado mediante programación en Matlab es el
filtrado y determinación de los rangos de las funciones. Los rangos hacen referencia a
los límites inferior y superior de las variables del eje de abscisas en las diferentes
funciones que se han tratado desde un punto de vista gráfico.
Estos rangos, una vez se ha determinado que son correctos, se incluyen en la
herramienta CARHI. Los rangos, en definitiva, indican los límites de las condiciones de
funcionamiento. Por tanto, el usuario de la herramienta tiene una orientación de las
condiciones mínimas y máximas a las que puede ceñirse a la hora de realizar cálculos.
Se trata de una ampliación respecto del MODHI, pues si bien éste contiene rangos
implícitamente (modifica las características introducidas por el usuario en caso de
encontrarse fuera de rango), el CARHI muestra los rangos explícitamente, orientando
al usuario antes de que introduzca cualquier variable. Esto es especialmente útil
cuando el usuario no está familiarizado con una característica concreta de un embalse o
central.
En la Figura 42 se muestra una impresión de pantalla del CARHI donde se
encuentran unos rangos para un cálculo determinado:
Figura 42. Rangos que proporciona la herramienta CARHI
5.3.4.2
Inclusión de gráficas en la herramienta CARHI. Curvas y colinas de
rendimiento.
Aparte del valor añadido de límites de rangos que proporciona la programación en
Matlab, otro valor añadido es la inclusión de gráficas de todas las funciones en las
hojas “Gráficas central” y “Gráficas embalse”. El programa MODHI, por ser antiguo,
carece de posibilidades gráficas que en el CARHI sí se han podido añadir. A lo largo
5 Modelado de las características hidroeléctricas
90
del apartado 5.3.2 se han mostrado ejemplos varios de gráficas obtenidas, por lo que no
será necesario volver a comentarlas en este apartado.
No obstante, algunas de las gráficas desarrolladas se corresponden con curvas y
colinas de rendimiento. Debido a que el programa MODHI no proporciona
rendimientos, ni gráficamente ni explícitamente desde un punto de vista analítico. Por
tanto, se ha considerado oportuno comentar esta ampliación dentro de este apartado.
En la Figura 43 se muestra una gráfica que relaciona el caudal por grupo en el eje de
las abscisas con el rendimiento de la turbina, para distintos saltos netos:
Figura 43. Curvas de rendimiento en relación al caudal por grupo y al salto neto
El código de programación en Matlab que desarrolla las gráficas de curvas de
rendimiento se adjunta en el anexo E.1.
Entre las líneas 80 y 88 del código en Matlab se puede observar que el rendimiento
de
la
turbina
se
ha
calculado
como
ηturbina =
P
,
ρ * g * Hn * Q *ηalternador
considerando el rendimiento del alternador constante e igual a 0.98 (igualmente en el
código en VBA donde se calcula el rendimiento, se incluye el rendimiento del
alternador igual a 0.98). Esta inclusión hace más realista el cálculo del rendimiento de
5 Modelado de las características hidroeléctricas
91
la turbina. Esto se aprecia en el análisis gráfico, puesto que las curvas de rendimiento
son bastante simétricas respecto de la vertical. En el futuro se pretende incluir curvas
de rendimiento del alternador.
No obstante, las curvas hubieran salido todavía más simétricas de haber
considerado un rango variable de valor mínimo de abscisas. Es decir, si en vez de
considerarse un valor de caudal mínimo orientativo como el 40% del caudal máximo
(ver línea 68 del código), se hubiera considerado valores de alrededor del 20% del
caudal máximo para aquellas centrales cuyas curvas de nivel de rendimiento abarcan
una pequeña diferencia de salto (ver Figura 44) y valores de alrededor del 60% del
caudal máximo para aquellas centrales cuyas curvas de nivel de rendimiento abarcan
una gran diferencia de salto (ver Figura 44), las curvas hubieran salido todavía más
simétricas. Esto no ha sido posible, pues se desconocen los valores mínimos reales de
los caudales, y el 40% de caudal máximo se considera una buena aproximación
orientativa de caudal mínimo.
Figura 44. Diferencia de salto que abarcan las curvas de nivel de rendimiento
Por otro lado, se ha procedido a realizar el cálculo gráfico de las colinas de
rendimiento, en las cuales se relaciona caudal por grupo, salto neto y rendimiento de la
turbina. El código de programación en Matlab que realiza este cálculo se incluye en el
anexo E.2.
5 Modelado de las características hidroeléctricas
92
La diferencia significativa frente a cualquier otro código de cálculo gráfico en 2D se
encuentra entre las líneas 98 y 127 del citado código. Merece la pena observar como se
usa la instrucción meshgrid para elaborar una malla de puntos de caudales unitarios y
saltos netos. Los saltos netos proceden de los límites mínimo y máximo de cortes (de
salto neto) de la curva que relaciona caudal y potencia (ver línea 100 de código), y los
caudales provienen de un conjunto de puntos generados en la línea 67 del código a
partir de los rangos mínimos y máximos proporcionados por la función que relaciona
salto neto con caudales máximos unitarios (ver línea 25 de código donde se encuentra
la instrucción load CoefHnQmax).
Una vez se ha elaborado la malla de puntos, se procede a realizar una interpolación
en 3D mediante la instrucción interp2 (ver la línea 107 de código) donde se generan
rendimientos de la turbina para la malla de puntos. El resultado gráfico se muestra en
la Figura 45.
Figura 45. Colina de rendimiento
5 Modelado de las características hidroeléctricas
93
Se observa a la izquierda de la figura la colina de rendimiento, siendo la gráfica de
la derecha su proyección sobre el plano XY. Esto ha sido realizado con las instrucciones
de generación de imágenes en 3D (entre las líneas 117 y 127 de código).
Cabe mencionar que la zona rojiza de la colina de rendimiento representa las
condiciones de funcionamiento, puesto que los rendimientos inferiores al 80% pueden
ser en general perjudiciales.
5.3.4.3
Ajuste de la función volumen útil – cota mediante el uso de splines
El programa MODHI proporciona implícitamente la cota como función del volumen
útil, ya que para hacer el cálculo realiza un proceso iterativo que se apoya en la función
explicita cota – volumen útil.
La ampliación que se ha realizado en la herramienta CARHI ha sido la inclusión de
la función explícita volumen útil – cota. Por tanto, el CARHI no sólo permite realizar
cálculos en donde se obtiene una cota a partir de un volumen útil dado, sino que
también proporciona los coeficientes de la función explícita, de tal modo que se puede
hacer uso de ellos y exportarlos a otras herramientas del entorno de Excel.
Asimismo, el ajuste de la función real volumen útil – cota no se ha realizado por una
aproximación polinómica, sino por un ajuste spline. Un spline (del inglés, tira fina) es
una curva definida a trozos mediante polinomios, siendo los puntos de cambio de
tramo coincidentes tanto en el valor como en la derivada primera. En general, los
polinomios del ajuste spline pueden ser de diferentes grados, pero el ajuste mediante
splines que se ha hecho en Matlab contiene mayoritariamente polinomios de tercer
grado.
El ajuste de interpolación spline es más preciso que un ajuste típico por una función
polinómica. De ahí que se use este tipo de interpolación en diversos ámbitos, como es
el desarrollo aerodinámico de los perfiles de los coches. En la Figura 46 se muestra una
comparativa de ajustes de una función de Iberdrola hecha mediante programación en
Matlab, donde se comprueba como el ajuste por spline (gráfica de la derecha) es más
preciso que el ajuste por una polinómica de quinto grado.
5 Modelado de las características hidroeléctricas
94
Figura 46. Comparativa entre un ajuste de 5º grado y un ajuste spline
El proceso llevado a cabo para obtener las funciones explícitas ha sido realizado
mediante programación en Matlab. El código de programación se ha incluido en el
anexo E.3. En dicho código se observa como, partiendo de una nube de puntos (ver
líneas 16 y 19 del código) procedentes de la función cota – volumen útil, se realiza un
proceso iterativo de ajuste mediante spline para obtener finalmente la función volumen
útil – cota.
El proceso iterativo se basa en un algoritmo de optimización donde se pretende
reducir el número de tramos de la función spline. De este modo, entre las líneas 57 y 60
del código se observa como para cada ciclo de la iteración se calcula el desvío de los
puntos del ajuste spline frente a la curva real y se selecciona el punto con mayor desvío
(contenido en la variables MaxDesvio) para realizar el siguiente tramo del proceso
iterativo. El proceso finaliza cuando ningún punto de la curva ajusta por Spline tiene
un error mayor de muy poco centímetros (línea 47 de código).
En la Figura 47 se muestra un caso ejemplo de ajuste mediante spline:
5 Modelado de las características hidroeléctricas
95
Figura 47. Ajuste spline
Se observa que el proceso de optimización ha generado tres tramos siendo los dos
puntos intermedios aquéllos donde había un mayor desvío en el proceso iterativo, por
lo que se forzó a la curva de ajuste a pasar por ellos. Además se observa que el
crecimiento de la curva tiene sentido físico porque es continuamente creciente y de
derivada creciente. La razón física se base en que en todo embalse tenemos que:
dV = Sdy Æ s =dV/dy
Por tanto, como la superficie proyectada siempre aumenta a medida que aumenta la
cota, la derivada ha de ser siempre creciente.
5.3.4.4
Obtención de más coeficientes energéticos
En los llamados Datos Variables del MODHI, comentados en el apartado 5.2.2, es
posible obtener el coeficiente energético ante unas condiciones de funcionamiento
concretas.
La ampliación que realiza la herramienta CARHI al respecto es la posibilidad de
obtener no sólo el coeficiente energético para unas condiciones de funcionamiento, sino
5 Modelado de las características hidroeléctricas
96
también los coeficientes energéticos a plena carga y a pleno rendimiento. En la Figura
48 se observan los distintos puntos a los que responde cada coeficiente energético:
Figura 48. Distintos coeficientes energéticos
Como ya quedó determinado en el apartado 2.5.7, el coeficiente energético es la
relación entre la energía y el volumen, que al fin y al cabo es la relación entre la
potencia y el caudal. Por otro lado, se pudo comprobar en el apartado 5.3.2.4 que la
relación entre caudal y potencia tiene un grado de libertad que lo fija el salto neto. Por
tanto, para un único salto neto se puede considerar infinidad de coeficientes
energéticos, siendo los más característicos los ya mencionados: el coeficiente de
energético de funcionamiento, el coeficiente energético de máximo rendimiento y el
coeficiente energético de plena carga.
En la Figura 48 se observa que el coeficiente energético para una potencia de
funcionamiento no tiene por qué coincidir con el coeficiente energético de plena carga,
en donde la potencia rondará los valores máximos admisibles. Del mismo modo,
tampoco tiene por qué coincidir con el coeficiente energético de máximo rendimiento,
siendo en este caso la potencia tal, que relacionada con el salto neto y el caudal dé
como resultado el rendimiento máximo (ver apartado 2.5.6). El coeficiente de máximo
rendimiento siempre será mayor que el de plena carga.
La programación en Visual Basic para proporcionar los coeficientes energéticos de
plena carga y de máximo rendimiento no es trivial. En el anexo D.10 se pueden
5 Modelado de las características hidroeléctricas
97
encontrar las subrutinas que realizan el cálculo bajo los nombres de Sub
HallaCoefEnergMxRto() y Sub HallaCoefEnergPlenaCarga().
Como se puede apreciar en el código, el algoritmo para obtener el coeficiente
energético de máximo rendimiento es el siguiente: en primer lugar, se calcula el caudal
unitario máximo (QMax) para el salto neto resultante de la iteración mediante la
función que relaciona salto neto con caudales máximos (ver apartado 5.3.2.5). Por otro
lado, el caudal mínimo unitario (QMin) no es función del salto neto, por lo que se
incluye en la subrutina mediante una declaración ByVal. A continuación, se procede a
realizar un barrido calculando coeficientes energéticos para distintos valores de caudal
unitario, partiendo del Qmin y llegando hasta el Qmax. Dicho barrido se realiza a
través de un bucle For donde se calcula el rendimiento para el caudal unitario de cada
ciclo y el salto neto resultante de las condiciones de funcionamiento. Mediante la
declaración de una condición If, se almacena el coeficiente energético máximo del
barrido en la variable CoefEnergMxRto.
En cuanto al cálculo del coeficiente energético de plena carga, se procede de un
modo análogo. En este caso no es necesario entrar dentro de un bucle, pues una vez se
halla el Qmax, basta con calcular la potencia unitaria correspondiente para dicho
caudal y para el salto neto de las condiciones de funcionamiento dadas (ver apartado
5.3.2.6), obteniendo el coeficiente energético a plena carga.
5.3.4.5
Características generales de cuencas, embalses y centrales
La herramienta CARHI proporciona información de características generales tanto
en las hojas de las cuencas existentes como en las hojas del embalse o central en
cuestión.
La información procede en gran parte de una investigación y recopilación de datos
realizada a lo largo de varias fuentes. Se trata de una ampliación que añade valor
añadido respecto del MODHI en tanto en cuanto hace más cercano y amable el uso de
la herramienta, a la par que sirve como fuente de información general.
En la Figura 49 se presenta una impresión de pantalla que contiene información
general:
5 Modelado de las características hidroeléctricas
Figura 49. Impresión de pantalla de características generales de una cuenca
98
5
Conclusiones
6 Conclusiones
6
100
Conclusiones
Hace tiempo tuve un profesor que me enseñó la técnica del llamado “20 – 80”. Más
que una técnica, se trata de una filosofía de vida. Se parte de la siguiente premisa: “se
emplea el 20% del tiempo en realizar el 80% de las cosas, y el 80% del tiempo en
realizar el 20% de las cosas”. Esto quiere decir que la mayor parte del tiempo (por
norma general) se dedica a realizar cosas que no tienen demasiada importancia en
comparación con el total de las cosas que hay que hacer. Por otro lado, mientras la vida
de una persona sea sostenible, es decir, mientras una persona sea capaz de hacer el
100% de las cosas que tiene que hacer, si dedica el 80% del tiempo a hacer el 20% de las
cosas, necesariamente (si despejamos la ecuación) será capaz de hacer el 80% de las
cosas en tan sólo un 20% del tiempo… ¿Cuál es la solución? La respuesta es inmediata:
dedicar dos 20% del tiempo, para así poder hacer el 160% de las cosas (y poder tener
un 60% de tiempo libre).
Desde luego esta no es una conclusión muy científica para un proyecto fin de
carrera, pero en cierto modo existe una filosofía de este tipo detrás de cualquier buen
proyecto fin de carrera. En el caso de realizar el proyecto a través de una empresa,
como es el caso, esta filosofía cobra todavía más importancia, pues el trabajo en una
empresa implica no sólo llevar a cabo un buen proyecto. Al realizar un proyecto en una
empresa es necesario cumplir los objetivos marcados por las necesidades de la
empresa. Si se realiza un proyecto muy bueno, pero que no aplica a lo que la empresa
necesita, el valor añadido que aporta es nulo.
Tengo la satisfacción de haber realizado un proyecto que no sólo sirve como modelo
genérico de gestión y cálculo de características de embalses y centrales hidroeléctricas,
sino que también tiene aplicación directa en la empresa. CARHI es una herramienta
que se va a usar, junto a otros programas y paquetes informáticos, en la gestión y
optimización de los recursos hidroeléctricos de Iberdrola.
Retomando la idea de la que parte esta conclusión de memoria, si no hubiera
aplicado mis cualidades personales basadas en la filosofía “20 – 80” a lo largo de este
curso académico, la herramienta CARHI no habría llegado a ser lo que es a la fecha de
terminación del proyecto. Durante el desarrollo del proyecto ha sido necesario abarcar
6 Conclusiones
101
muy diversos temas, tanto teóricos como prácticos, tanto físicos como técnicos, tanto
matemáticos como ingenieriles, que había que integrar y conciliar entre sí. Asimismo,
ha sido necesario mantener una comunicación constante y fluida con el equipo de
Gestión de la Energía de Iberdrola y, en concreto, con mis directores de proyecto
(Rafael Bellido y Alejandro Perea). Se trata de un proyecto con muchos factores
internos y externos que han sido gestionados del modo más eficiente posible para
poder llevar a buen puerto el trabajo.
En conclusión, el proyecto realizado de modelado de características de embalses y
centrales hidroeléctricas ha resultado exitoso y satisfactorio, tanto desde el punto de
vista del enriquecimiento académico y personal, como desde el punto de vista de su
aplicación directa y práctica a las necesidades de Iberdrola.
6
Links y bibliografía
7 Links y bibliografía
7
103
Links y bibliografía
Nota: este proyecto contiene muchos conocimientos que he aprendido a
través del equipo de Gestión de la Energía y, concretamente, a través de
mis directores Rafael Bellido y Alejandro Perea. Se trata lógicamente de
conocimientos que no se pueden plasmar como referencia bibliográfica en
este apartado.
[UNIP91] UNIPEDE – Terminologie. Edición de 1991.
[IBER00]
Características de los aprovechamientos hidroeléctricos. Iberdrola.
Edición de 2000.
[CENT94] Centrales hidroeléctricas I. Conceptos y componentes hidráulicos.
Iberdrola. Edición de 1994.
[CENT94] Centrales hidroeléctricas I. Turbinas hidráulicas. Iberdrola.
Edición de 1994.
www.ree.es
www.cne.es
www.mityc.es
www.mma.es
www.cedex.es
www.chebro.es
www.chnorte.es
www.chtajo.es
www.chduero.es
www.chj.es
7
Agradecimientos
8 Agradecimientos
8
105
Agradecimientos
Como en muchos aspectos de la vida, lo más importante no siempre ocupa el primer
puesto o no siempre se dice en primer lugar. Hay mucha gente a la que tengo mucho
que agradecer y me resulta una lástima que tenga que ser en una de las últimas
páginas de mi memoria de proyecto. Si por mí fuera, les daría las gracias en la primera
página.
En primer lugar, gracias a mis directores de proyecto: Rafael Bellido y Alejandro
Perea. Estoy completamente convencido de que hubiera sido imposible tener unos
directores mejores. Quizá iguales, pero no mejores.
Gracias también a todo el equipo de Gestión de la Energía de Iberdrola y, en
concreto, a Claudio Chaves, Javier Paradinas, Manolo Rey y Pilar Vázquez, por el
apoyo que me habéis brindado siempre.
Gracias a Carlos Batlle, Miguel Vázquez y Pablo por ser los primeros en formarme
en el mundo profesional. Guardo un grato recuerdo de mi experiencia en el IIT, no sólo
en el ámbito profesional, sino también por el impacto que habéis tenido en mi persona.
Gracias también a todo el profesorado de ICAI. Gracias por haber influido tan
positivamente en mi ámbito académico durante estos cinco años y haberme ayudado a
estar a las puertas de ser ingeniero industrial del ICAI.
Gracias a los que siempre estáis ahí. Los que sois mis hermanos, puesto que no los
tengo de sangre. Los que me conocéis muy bien, en lo bueno y en lo malo. Sin vosotros,
yo seguramente no sería el mismo. Sois mis amigos con mayúsculas. Siento tener que
crear diferencias, pero es necesario mencionas en particular a Alberto Gómez, por el
hecho de haberme acompañado en paralelo en mi caminar por Iberdrola.
Gracias al resto de personas con las que he tenido la suerte de cruzarme en mi vida.
Soy feliz y, sin duda, habéis tenido algo que ver en esa felicidad.
Y, por último, gracias a las dos personas más especiales de mi vida: a mi madre y a
mi padre. Si dije que sin mis amigos yo seguramente no sería el mismo, sin vosotros
está claro que no lo sería. Pero eso, ya lo sabéis.
Anexos
A
Códigos de programación en
Fortran
A Códigos de programación en Fortran
A Códigos de programación en Fortran
A.1
EMBALSES.CAR
CLAVES DE EMBALSES Y DATOS EN EL BASE
****************************************************************************
S001 SISTEMA DUERO
010
EMBALSES
OOO
--CERNADILLA
010
VALPARAISO
020
S.M.AGAVANZAL
025
ESLA
030
.
.
.
****************************************************************************
S999................
A.2
CENTRALES.CAR
CLAVES DE CENTRALES Y DATOS EN LA BASE
****************************************************************************
S001 SISTEMA DUERO
017
EMBALSES
OOO
--CERNADILLA
010
VALPARAISO
020
AGAVANZAL 1
025
.
.
.
****************************************************************************
S999................
A.3
CARHI.FOR
Program carhi
C
C
C
C
Programa para cargar datos de embalses de IBERDROLA
Autor: Juan Palomares
PARAMETER(NEMBMX=14,NSISMX=7,NCURMX=40,NVINDMX=2,NCOEFMX=5)
C
INTEGER J,NEMB(NSISMX),SS(NSISMX),OOO(NEMBMX,NSISMX)
CHARACTER*20 SISTEM(NSISMX),EMB(NEMBMX,NSISMX)
C
CHARACTER*5 INST
CHARACTER*1 LINEA,EOC(2)/'E','C'/
CHARACTER*2 FUN
CHARACTER*2 FAUX(10)/'F1','F2','F1','F2','F3','F4','F5','F6',
.'F7','F8'/
REAL*4 VREF(NCURMX),VLIM(NCURMX),VVAR(NVINDMX,NCURMX)
REAL*4 COEF(NCOEFMX,NCURMX)
INTEGER NCURVAS,IVAR,IGRA,ISTAT
LOGICAL*2 IREF,ILIM
CHARACTER*30 NOMFUN(10)
NOMFUN(1)='VOLUMEN ÚTIL DE EMBALSE'
NOMFUN(2)='VOLUMEN TOTAL DE EMBALSE'
NOMFUN(3)='COTA DE DESAGÜE (AFTERBAY)'
NOMFUN(4)='PÉRDIDAS DE CARGA'
NOMFUN(5)='POTENCIA LÍMITE'
NOMFUN(6)='CAUDAL LÍMITE'
NOMFUN(7)='POTENCIA DE GENERACIÓN'
NOMFUN(8)='CAUDAL TURBINADO'
NOMFUN(9)='POTENCIA DE BOMBEO'
NOMFUN(10)='CAUDAL BOMBEADO'
C
C
C
C
*****************************************************************
APERTURA DE LOS ARCHIVOS DE CODIGOS DE EMBALSE Y DE CENTRAL
108
A Códigos de programación en Fortran
C
OPEN(11,FILE='EMBALSES.CAR',STATUS='OLD',READONLY)
OPEN(12,FILE='CENTRALES.CAR',STATUS='OLD',READONLY)
C
C
C
APERTURA DE LOS ARCHIVOS DE SALIDA DE ESTE PROGRAMA
OPEN(1,FILE='F1.SAL')
OPEN(2,FILE='F2.SAL')
OPEN(3,FILE='F3.SAL')
OPEN(4,FILE='F4.SAL')
OPEN(5,FILE='F5.SAL')
OPEN(6,FILE='F6.SAL')
OPEN(7,FILE='F7.SAL')
OPEN(8,FILE='F8.SAL')
OPEN(9,FILE='F9.SAL')
OPEN(10,FILE='F10.SAL')
C
C
C
C
C
*****************************************************************
LECTURA DE CODIGOS DE EMBALSES
READ(11,90) LINEA
FORMAT(A1)
90
C
C
C
BUCLE DE SISTEMAS
NEOC=1
NSIS=0
DO 10 ISIS=1,NSISMX
C
READ(11,90) LINEA
READ(11,100) SS(ISIS),SISTEM(ISIS),NEMB(ISIS)
FORMAT(1X,I3,2X,A20,I3)
100
C
IF(SS(ISIS).NE.999) THEN
C
DO 111 K=1,2
C
101
102
103
.
104
.
105
106
.
.
107
.
.
FORMAT(3X,'SISTEMA:',2X,A20)
WRITE(K,101) SISTEM(ISIS)
FORMAT('**************************************************')
WRITE(K,102)
FORMAT(1X,'FUNCIÓN',27X,'EMBALSE',16X,'GRADO',2X,
'NCURVAS',2X,'IREF',2X,'ILIM',2X,'IVAR',2X,'ISTAT')
WRITE(K,103)
FORMAT(1X,'-------',27X,'-------',16X,'-----',2X,
'-------',2X,'----',2X,'----',2X,'----',2X,'-----')
WRITE(K,104)
FORMAT('---------------------------------------------------')
WRITE(K,105)
FORMAT(1X,'J',2X,'VREF(J)',5X,'VLIM(J)',5X,'VVAR(1,J)',5X,
'VVAR(2,J)',3X,'COEF(1,J)',3X,'COEF(2,J)',3X,'COEF(3,J)',
3X,'COEF(4,J)',3X,'COEF(5,J)')
WRITE(K,106)
FORMAT(1X,'-',2X,'-------',5X,'-------',5X,'---------',5X,
'---------',3X,'---------',3X,'---------',3X,'---------',
3X,'---------',3X,'---------')
WRITE(K,107)
C
111
CONTINUE
C
NSIS=NSIS+1
READ(11,90) LINEA
READ(11,90) LINEA
C
C
C
BUCLE DE EMBALSES
DO 20 IEMB=1,NEMB(ISIS)
C
C
200
READ(11,200) EMB(IEMB,ISIS),OOO(IEMB,ISIS)
FORMAT(A20,I3)
C
201
C
C
FORMAT(I1,A1,I3.3)
WRITE(INST,201) ISIS,EOC(NEOC),OOO(IEMB,ISIS)
BUCLE DE FUNCIONES
DO 30 K=1,2
109
A Códigos de programación en Fortran
FUN=FAUX(K)
CALL HM$CURVAS(INST,FUN,NCURVAS,IREF,ILIM,IVAR,IGRA,VREF,
VLIM,VVAR,COEF,ISTAT)
.
C
300
FORMAT(1X,A30,4X,A20,3X,I1,6X,I1,8X,L2,4X,L2,
4X,I1,5X,I5)
WRITE(K,300) NOMFUN(K),EMB(IEMB,ISIS),IGRA,
NCURVAS,IREF,ILIM,IVAR,ISTAT
.
.
C
DO 302 J=1,NCURMX
FORMAT(1X,I3,9(2X,E10.3))
WRITE(K,301) J,VREF(J),VLIM(J),VVAR(1,J),VVAR(2,J),
COEF(1,J),COEF(2,J),COEF(3,J),COEF(4,J),COEF(5,J)
IF(J.EQ.NCURVAS) THEN
GO TO 30
ENDIF
CONTINUE
301
.
C
C
C
302
C
30
CONTINUE
C
20
CONTINUE
108
FORMAT('=====================================================')
DO 112 K=1,2
WRITE(K,108)
CONTINUE
C
112
C
ELSE
C
109
WRITE(*,*) ' FIN DE LECTURA DE FICHERO DE CODIGOS DE EMBALSES'
WRITE(*,109) NSIS
FORMAT(3X,'SE HAN LEIDO',2X,I3,' SISTEMAS')
GO TO 980
C
ENDIF
C
10
C
C
C
C
C
CONTINUE
FIN DE BUCLES DE EMBALSES Y SISTEMAS
*****************************************************************
980
CONTINUE
STOP
END
C
C
C
*****************************************************************
A.4
CARHICEN.FOR
Program carhicen
C
C
C
C
Programa para cargar datos de centrales de IBERDROLA
Autor: Juan Palomares
PARAMETER(NCENMX=19,NSISMX=5,NCURMX=40,NVINDMX=2,NCOEFMX=5)
C
INTEGER J,NCEN(NSISMX),SS(NSISMX),OOO(NCENMX,NSISMX)
CHARACTER*20 SISTEM(NSISMX),CEN(NCENMX,NSISMX)
C
CHARACTER*5 INST
CHARACTER*1 LINEA,EOC(2)/'E','C'/
CHARACTER*2 FUN
CHARACTER*2 FAUX(10)/'F1','F2','F1','F2','F3','F4','F5','F6',
.'F7','F8'/
REAL*4 VREF(NCURMX),VLIM(NCURMX),VVAR(NVINDMX,NCURMX)
REAL*4 COEF(NCOEFMX,NCURMX)
INTEGER NCURVAS,IVAR,IGRA,ISTAT
LOGICAL*2 IREF,ILIM
CHARACTER*30 NOMFUN(10)
NOMFUN(1)='VOLUMEN ÚTIL DE EMBALSE'
NOMFUN(2)='VOLUMEN TOTAL DE EMBALSE'
NOMFUN(3)='COTA DE DESAGÜE (AFTERBAY)'
NOMFUN(4)='PÉrDIDAS DE CARGA'
NOMFUN(5)='POTENCIA LÍMITE'
NOMFUN(6)='CAUDAL LÍMITE'
110
A Códigos de programación en Fortran
NOMFUN(7)='POTENCIA DE GENERACIÓN'
NOMFUN(8)='CAUDAL TURBINADO'
NOMFUN(9)='POTENCIA DE BOMBEO'
NOMFUN(10)='CAUDAL BOMBEADO'
C
C
C
C
C
*****************************************************************
APERTURA DE LOS ARCHIVOS DE CODIGOS DE EMBALSE Y DE CENTRAL
OPEN(11,FILE='EMBALSES.CAR',STATUS='OLD',READONLY)
OPEN(12,FILE='CENTRALES.CAR',STATUS='OLD',READONLY)
C
C
C
APERTURA DE LOS ARCHIVOS DE SALIDA DE ESTE PROGRAMA
OPEN(1,FILE='F1.SAL')
OPEN(2,FILE='F2.SAL')
OPEN(3,FILE='F3.SAL')
OPEN(4,FILE='F4.SAL')
OPEN(5,FILE='F5.SAL')
OPEN(6,FILE='F6.SAL')
OPEN(7,FILE='F7.SAL')
OPEN(8,FILE='F8.SAL')
OPEN(9,FILE='F9.SAL')
OPEN(10,FILE='F10.SAL')
C
C
C
C
C
*****************************************************************
LECTURA DE CODIGOS DE CENTRALES
READ(12,90) LINEA
FORMAT(A1)
90
C
C
C
BUCLE DE SISTEMAS
NEOC=2
NSIS=0
DO 10 ISIS=1,NSISMX
C
READ(12,90) LINEA
READ(12,100) SS(ISIS),SISTEM(ISIS),NCEN(ISIS)
FORMAT(1X,I3,2X,A20,I3)
100
C
IF(SS(ISIS).NE.999) THEN
C
DO 111 K=3,10
C
101
102
103
.
104
.
105
106
.
.
107
.
.
FORMAT(3X,'SISTEMA:',2X,A20)
WRITE(K,101) SISTEM(ISIS)
FORMAT('**************************************************')
WRITE(K,102)
FORMAT(1X,'FUNCIÓN',27X,'CENTRAL',16X,'GRADO',2X,
'NCURVAS',2X,'IREF',2X,'ILIM',2X,'IVAR',2X,'ISTAT')
WRITE(K,103)
FORMAT(1X,'-------',27X,'-------',16X,'-----',2X,
'-------',2X,'----',2X,'----',2X,'----',2X,'-----')
WRITE(K,104)
FORMAT('---------------------------------------------------')
WRITE(K,105)
FORMAT(1X,'J',2X,'VREF(J)',5X,'VLIM(J)',5X,'VVAR(1,J)',5X,
'VVAR(2,J)',3X,'COEF(1,J)',3X,'COEF(2,J)',3X,'COEF(3,J)',
3X,'COEF(4,J)',3X,'COEF(5,J)')
WRITE(K,106)
FORMAT(1X,'-',2X,'-------',5X,'-------',5X,'---------',5X,
'---------',3X,'---------',3X,'---------',3X,'---------',
3X,'---------',3X,'---------')
WRITE(K,107)
C
111
CONTINUE
C
NSIS=NSIS+1
READ(12,90) LINEA
READ(12,90) LINEA
C
C
C
BUCLE DE CENTRALES
DO 20 ICEN=1,NCEN(ISIS)
C
C
111
A Códigos de programación en Fortran
READ(12,200) CEN(ICEN,ISIS),OOO(ICEN,ISIS)
FORMAT(A20,I3)
200
C
201
FORMAT(I1,A1,I3.3)
WRITE(INST,201) ISIS,EOC(NEOC),OOO(ICEN,ISIS)
C
C
.
BUCLE DE FUNCIONES
DO 30 K=3,10
FUN=FAUX(K)
CALL HM$CURVAS(INST,FUN,NCURVAS,IREF,ILIM,IVAR,IGRA,VREF,
VLIM,VVAR,COEF,ISTAT)
C
300
FORMAT(1X,A30,4X,A20,3X,I3,4X,I3,6X,L2,4X,L2,
4X,I3,3X,I5)
WRITE(K,300) NOMFUN(K),CEN(ICEN,ISIS),IGRA,
NCURVAS,IREF,ILIM,IVAR,ISTAT
.
.
C
DO 302 J=1,NCURMX
FORMAT(1X,I3,9(2X,E10.3))
WRITE(K,301) J,VREF(J),VLIM(J),VVAR(1,J),VVAR(2,J),
COEF(1,J),COEF(2,J),COEF(3,J),COEF(4,J),COEF(5,J)
CONTINUE
301
.
302
C
30
CONTINUE
C
20
CONTINUE
108
FORMAT('=====================================================')
DO 112 K=3,10
WRITE(K,108)
CONTINUE
C
112
C
ELSE
C
109
WRITE(*,*) ' FIN DE LECTURA DE FICHERO DE CODIGOS DE CENTRALES'
WRITE(*,109) NSIS
FORMAT(3X,'SE HAN LEIDO',2X,I3,' SISTEMAS')
GO TO 980
C
ENDIF
C
10
C
C
C
C
CONTINUE
FIN DE BUCLES DE CENTRALES Y SISTEMAS
980
*****************************************************************
CONTINUE
STOP
END
C
C
C
*****************************************************************
A.5
CARHIRESTOS.FOR
Program carhirestos
C
C
C
C
Programa para cargar resto de datos de embalses de IBERDROLA
Autor: Juan Palomares
PARAMETER(NEMBMX=14,NSISMX=7)
C
C
C
C
C
INTEGER NEMB(NSISMX),SS(NSISMX),OOO(NEMBMX,NSISMX)
CHARACTER*20 SISTEM(NSISMX),EMB(NEMBMX,NSISMX)
CHARACTER*1 SIS
CHARACTER*3 EMBALSE
CHARACTER*1 LINEA
REAL*4 COTMINEX,COTRGSUPVOLTOT,COTRGINFVOLTOT
REAL*4 COTMAXNOR,COTMINNOR
*****************************************************************
APERTURA DE LOS ARCHIVOS DE CODIGOS DE EMBALSE Y DE CENTRAL
OPEN(11,FILE='EMBALSES.CAR',STATUS='OLD',READONLY)
C
C
APERTURA DEL ARCHIVO DE SALIDA DE ESTE PROGRAMA
112
A Códigos de programación en Fortran
C
OPEN(13,FILE='F11.SAL')
C
C
C
C
C
*****************************************************************
LECTURA DE CODIGOS DE EMBALSES
READ(11,90) LINEA
FORMAT(A1)
90
C
C
C
BUCLE DE SISTEMAS
NSIS=0
DO 10 ISIS=1,NSISMX
C
READ(11,90) LINEA
READ(11,100) SS(ISIS),SISTEM(ISIS),NEMB(ISIS)
FORMAT(1X,I3,2X,A20,I3)
100
C
IF(SS(ISIS).NE.999) THEN
C
101
102
103
.
104
.
FORMAT(3X,'SISTEMA:',2X,A20)
WRITE(13,101) SISTEM(ISIS)
FORMAT('**************************************************')
WRITE(13,102)
FORMAT(1X,'COTMINEX',2X,'COTRGSUPVOLTOT',2X,'COTRGINFVOLTOT',
1X,'COTMAXNOR',2X,'COTMINNOR')
WRITE(13,103)
FORMAT(1X,'--------',2X,'--------------',2X,'-------------',
1X,'---------',2X,'---------')
WRITE(13,104)
C
NSIS=NSIS+1
READ(11,90) LINEA
READ(11,90) LINEA
C
C
C
BUCLE DE EMBALSES
DO 20 IEMB=1,NEMB(ISIS)
C
C
READ(11,200) EMB(IEMB,ISIS),OOO(IEMB,ISIS)
FORMAT(A20,I3)
200
C
C
WRITE(SIS,'(I1)') ISIS
WRITE(EMBALSE,'(I3.3)') OOO(IEMB,ISIS)
C
COTMINEX=HM$COTMIN(SIS,EMBALSE)
COTRGSUPVOLTOT=HM$COTMID(SIS,EMBALSE)
COTRGINFVOLTOT=HM$COTMID1(SIS,EMBALSE)
COTMAXNOR=HM$COTMAX(SIS,EMBALSE)
COTMINNOR=HM$COTMXT(SIS,EMBALSE)
C
201
.
FORMAT(5(1X,E13.6),1X,A20)
WRITE(13,201) COTMINEX,COTRGSUPVOLTOT,COTRGINFVOLTOT,
COTMAXNOR,COTMINNOR,EMB(IEMB,ISIS)
C
20
CONTINUE
108
FORMAT('=====================================================')
WRITE(13,108)
C
C
ELSE
C
109
WRITE(*,*) ' FIN DE LECTURA DE FICHERO DE CODIGOS DE EMBALSES'
WRITE(*,109) NSIS
FORMAT(3X,'SE HAN LEIDO',2X,I3,' SISTEMAS')
GO TO 980
C
ENDIF
C
10
C
C
C
C
CONTINUE
FIN DE BUCLES DE EMBALSES
*****************************************************************
113
A Códigos de programación en Fortran
C
980
CONTINUE
STOP
END
C
C
C
*****************************************************************
A.6
CARHICENRESTOS.FOR
Program carhicenrestos
C
C
C
C
Programa para cargar resto de datos de centrales de IBERDROLA
Autor: Juan Palomares
PARAMETER(NCENMX=19,NSISMX=5)
C
INTEGER NEMB(NSISMX),SS(NSISMX),OOO(NCENMX,NSISMX)
CHARACTER*20 SISTEM(NSISMX),EMB(NCENMX,NSISMX)
CHARACTER*1 SIS
CHARACTER*3 CENTRAL
CHARACTER*1 LINEA
REAL*4 NGGEN,NGBOM,PMXGEN,PMXBOM,COTADES
REAL*4 COTMINEMBAA,COTMAXEMBAAB
REAL*4 COTMAXEMBAA,COTMINEMBAAB
*****************************************************************
C
C
C
C
APERTURA DE LOS ARCHIVOS DE CODIGOS DE CENTRAL Y DE CENTRAL
OPEN(11,FILE='CENTRALES.CAR',STATUS='OLD',READONLY)
C
C
C
APERTURA DEL ARCHIVO DE SALIDA DE ESTE PROGRAMA
OPEN(13,FILE='F12.SAL')
C
C
C
C
C
*****************************************************************
LECTURA DE CODIGOS DE CENTRALES
READ(11,90) LINEA
FORMAT(A1)
90
C
C
C
BUCLE DE SISTEMAS
NSIS=0
DO 10 ISIS=1,NSISMX
C
READ(11,90) LINEA
READ(11,100) SS(ISIS),SISTEM(ISIS),NEMB(ISIS)
FORMAT(1X,I3,2X,A20,I3)
100
C
IF(SS(ISIS).NE.999) THEN
C
101
102
103
.
.
104
.
FORMAT(3X,'SISTEMA:',2X,A20)
WRITE(13,101) SISTEM(ISIS)
FORMAT('**************************************************')
WRITE(13,102)
FORMAT(1X,'NGGEN',2X,'NGBOM',2X,'PMXGEN',2X,'PMXBOM',2X,
'COTADES',2X,'COTMINEMBAA',2X,'COTMAXEMBAAB',2X,
'COTMAXEMBAA',2X,'COTMINEMBAAB')
WRITE(13,103)
FORMAT(1X,'--------',2X,'--------------',2X,'-------------',
1X,'---------',2X,'---------')
WRITE(13,104)
C
NSIS=NSIS+1
READ(11,90) LINEA
READ(11,90) LINEA
C
C
C
BUCLE DE CENTRALES
DO 20 IEMB=1,NEMB(ISIS)
C
C
200
READ(11,200) EMB(IEMB,ISIS),OOO(IEMB,ISIS)
FORMAT(A20,I3)
114
A Códigos de programación en Fortran
C
C
WRITE(SIS,'(I1)') ISIS
WRITE(CENTRAL,'(I3.3)') OOO(IEMB,ISIS)
C
NGGEN=HM$NGRUPOS(SIS,CENTRAL)
NGBOM=HM$NGRB(SIS,CENTRAL)
PMXGEN=HM$POTMAX(SIS,CENTRAL)
PMXBOM=HM$PBMAX(SIS,CENTRAL)
COTADES=HM$COTADES(SIS,CENTRAL)
COTMINEMBAA=HM$CEMIN(SIS,CENTRAL)
COTMAXEMBAAB=HM$CEAAMAX(SIS,CENTRAL)
COTMAXEMBAA=HM$CEMAX(SIS,CENTRAL)
COTMINEMBAAB=HM$CEAAMIN(SIS,CENTRAL)
C
201
.
FORMAT(7(1X,E13.6))
WRITE(13,201) NGGEN,NGBOM,PMXGEN,PMXBOM,COTADES,
COTMINEMBAA,COTMAXEMBAAB
.
FORMAT(2(1X,E13.6),1X,A20)
WRITE(13,205) COTMAXEMBAA,COTMINEMBAAB,
EMB(IEMB,ISIS)
C
205
C
20
CONTINUE
108
FORMAT('=====================================================')
WRITE(13,108)
C
C
ELSE
C
109
WRITE(*,*) ' FIN DE LECTURA DE FICHERO DE CODIGOS DE CENTRALES'
WRITE(*,109) NSIS
FORMAT(3X,'SE HAN LEIDO',2X,I3,' SISTEMAS')
GO TO 980
C
ENDIF
C
10
C
C
C
C
C
FIN DE BUCLES DE CENTRALES
*****************************************************************
980
C
C
C
CONTINUE
CONTINUE
STOP
END
*****************************************************************
115
B
Control de características
extraídas del MODHI mediante
programación en Visual Basic
B Control de características extraídas del MODHI mediante programación en Visual Basic
117
B Control de características extraídas del MODHI mediante
programación en Visual Basic
B.1
Control de las características de embalses y centrales hidroeléctricas
Sub Macro1()
'Borrar nombre función
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(2).Cells
If Celda.Value = "VOLUMEN" Then
Celda.Select
Range(Selection, Selection.Offset(0, 3)).Select
Selection.ClearContents
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Macro2()
'Corre una celda a la izquierda nombres muy largos
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(13).Cells
If Not Celda.Value = "" Then
Celda.Select
Range(Selection.Offset(0, -10), Selection).Select
Selection.Cut
Celda.Select
Range(Selection.Offset(0, -11), Selection.Offset(0, -1)).Select
ActiveSheet.Paste
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Macro3()
'Corre una celda a la izquierda nombres largos
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(12).Cells
If Not Celda.Value = "" Then
Celda.Select
Range(Selection.Offset(0, -10), Selection).Select
Selection.Cut
Celda.Select
Range(Selection.Offset(0, -11), Selection.Offset(0, -1)).Select
ActiveSheet.Paste
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Macro4()
'Corre encabezamiento a la derecha
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(3).Cells
If Celda.Value = "EMBALSE" Then
Celda.Select
Range(Selection, Selection.Offset(0, 6)).Select
Selection.Cut
Celda.Select
Range(Selection.Offset(0, 2), Selection.Offset(0, 8)).Select
ActiveSheet.Paste
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Macro5()
B Control de características extraídas del MODHI mediante programación en Visual Basic
118
'Preparación para que funcione bien macro de borrar ceros
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(8).Cells
If Celda.Value = "" Then
Celda.Select
Selection.Value = "SISTEMA"
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Macro6()
'Borrar ceros
Dim i As Integer
Dim Celda As Object
Do
For Each Celda In ActiveSheet.Columns(8).Cells
If Celda.Value = 0 Then
Celda.Select
Exit For
End If
Next Celda
For i = 1 To Selection.CurrentRegion.Rows.Count
If ActiveCell.Value = 0 Then
ActiveCell.Select
Selection.EntireRow.Delete
End If
Next i
Loop Until IsEmpty(ActiveCell.Value)
End Sub
Sub Macro7()
' Borra rayitas de subrayado que empiezan en col1
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(1).Cells
If Not Celda.Value = "" Then
Celda.Select
Range(Selection, Selection.Offset(0, 20)).Select
Selection.ClearContents
End If
End Sub
Sub Macro8()
' Borra rayitas de subrayado que empiezan en col2
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(2).Cells
If Celda.Value = "-" Then
Celda.Select
Range(Selection, Selection.Offset(0, 20)).Select
Selection.ClearContents
End If
If Celda.Value = "-------" Then
Celda.Select
Range(Selection, Selection.Offset(0, 20)).Select
Selection.ClearContents
End If
End Sub
B.2
Preparación y organización de las características para implementarlas en
archivos .mat
Sub Matlb()
'Enumerar embalses
Dim cont As Integer
Dim Celda As Object
cont = 1
For Each Celda In ActiveSheet.Columns(2).Cells
If Celda.Value = 1 Then
Celda.Select
Selection.Offset(0, -1).Select
Selection.Value = cont
cont = cont + 1
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
B Control de características extraídas del MODHI mediante programación en Visual Basic
End Sub
Sub Matlb2()
'Preparación
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(2).Cells
If Celda.Value = "SISTEMA:" Then
Celda.Select
Selection.ClearContents
Celda.Offset(2, 0).Select
Selection.ClearContents
Celda.Offset(3, 0).Select
Selection.ClearContents
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Matlb3()
'Cortar y pegar lo necesario para pintar
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(2).Cells
If Not Celda.Value = "" Then
'Copio índices
Celda.Select
Range(Selection.Offset(0, -1), Selection).Select
Selection.Copy
Celda.Select
Selection.Offset(0, 12).Select
ActiveSheet.Paste
'Copio coeficientes
Celda.Select
Range(Selection.Offset(0, 5), Selection.Offset(0, 9)).Select
Selection.Copy
Celda.Select
Selection.Offset(0, 14).Select
ActiveSheet.Paste
End If
If Celda.Value = "STOP" Then
Exit For
End If
Next Celda
End Sub
Sub Matlb4()
'Hago lista con índices embalses
Dim Celda As Object
For Each Celda In ActiveSheet.Columns(1).Cells
If Not Celda.Value = "" Then
'Copio nombres
Celda.Select
Selection.Offset(-1, 4).Select
Selection.Copy
Celda.Select
Selection.Offset(0, 40).Select
ActiveSheet.Paste
End If
Next Celda
End Sub
119
C
Control analítico y gráfico de las
características hidroeléctricas
mediante programación en
Matlab
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
121
C Control analítico y gráfico de las características hidroeléctricas
mediante programación en Matlab
C.1
Función que relaciona la cota con el volumen útil y total del embalse
%Autor: Juan Palomares
%Cota - volumen útil y cota - volumen total superpuestas
%%
function CotaVolUtilyTotal()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de embalses (col2)
% y sus respectivos índices (col3)
load Embalses
%Cargo VUtil: col1=índice embalse, col2 - col6 coef en orden
%[coef0,...,coefn], col7=cotmax, col8=cotmin, col9=cotminexplotac
%y col10=cota de referencia
load VUtil
%Cargo VTotal: col1=índice embalse, col2=índice curvas,
%col3 - col7= coeficientes, col8=cota de referencia, col9=cotmax,
%col10=cotmin, col11=cotminexplotac, col12=cotrgsup (si hay dos tramos)
%y col13=cotrginf (si hay tres tramos)
load VTotal
%Cargo ajuste de valdecañas
load xValdecanas
load yValdecanas
%%
%Número de embalses
NEmbalses = length(VUtil);
%Número de curvas de cota - volumen total
NVolTot = length(VTotal);
%Número de puntos que pintaré
NPuntos = 1000;
%Matriz de coeficientes de cota - volumen útil en el orden
%[coefn, coef(n-1),...,coef0] para usar polyval
for CfUtilCt =1: NEmbalses
CoefUtil(CfUtilCt,1:5) = VUtil(CfUtilCt,2:6);
end
CoefUtil= fliplr(CoefUtil);
%Matriz de coeficientes de cota - volumen total en el orden
%[coefn, coef(n-1),...,coef0] para usar polyval
Cambio = 0;
for CfTotCt =1: NVolTot
%Pongo índices para luego saber cuántas curvas pongo en cada gráfica
if VTotal(CfTotCt,2) == 1
Cambio = Cambio + 1;
CoefTot(CfTotCt,6) = Cambio;
CoefTot(CfTotCt,1:5) = VTotal(CfTotCt,3:7);
else
CoefTot(CfTotCt,6) = Cambio;
CoefTot(CfTotCt,1:5) = VTotal(CfTotCt,3:7);
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
122
end
end
CoefTot= fliplr(CoefTot);
%Matriz de abscisas de cota - volumen útil
for CfUtilCt =1: NEmbalses
%Para generar las ordenadas
x1(CfUtilCt,1:NPuntos) = linspace(VUtil(CfUtilCt,9),VUtil(CfUtilCt,7),NPuntos)VUtil(CfUtilCt,10);
%Para pintar desde VUtil igual a cero
x(CfUtilCt,1:NPuntos) = linspace(VUtil(CfUtilCt,9),VUtil(CfUtilCt,7),NPuntos);
end
%Matriz de abscisas de cota - volumen total
for CfTotCt =1: NVolTot
%Para generar las ordenadas
xt1(CfTotCt,1:NPuntos) = linspace(VTotal(CfTotCt,10),VTotal(CfTotCt,9),NPuntos)VTotal(CfTotCt,8);
%Para pintar desde VTotal igual a cero
xt(CfTotCt,1:NPuntos) = linspace(VTotal(CfTotCt,10),VTotal(CfTotCt,9),NPuntos);
end
%Matriz de ordenadas de cota - volumen útil
for CfUtilCt =1: NEmbalses
y(CfUtilCt,1:NPuntos)= polyval(CoefUtil(CfUtilCt,1:5),x1(CfUtilCt,1:NPuntos));
end
%Matriz de ordenadas de cota - volumen total
for CfTotCt =1: NVolTot
yt(CfTotCt,1:NPuntos)= polyval(CoefTot(CfTotCt,2:6),xt1(CfTotCt,1:NPuntos));
end
%%
%Gráficas de cota - volumen útil y cota - volumen total superpuestas
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = 1;
Cont = 0;
for CfTotCt =1: NVolTot
%Uso índices para saber cuántas curvas pongo en cada gráfica
if CoefTot(CfTotCt,1) ~= Antiguo
title (Embalses(Antiguo,2),'FontSize',17);
xlabel ('Cota (msnm)', 'FontSize',15);
ylabel('Volumen (hm^{3})','FontSize',15);
plot (x(Antiguo,1:NPuntos),y(Antiguo,1:NPuntos),'r','linewidth',2);
Max = round(max(y(Antiguo,1:NPuntos)));
text(x(Antiguo,NPuntos),y(Antiguo,NPuntos),horzcat('\rightarrow
','[',num2str(Max),' hm^{3}',',',num2str(x(Antiguo,NPuntos)),'msnm]'));
if Cont == 1
%Si VUtil coincide con VTotal, sólo pinto VUtil. Como no filtra
%Cernadilla (1) ni los Torrejón (34 y 35), lo meto a mano
Dif(1:NPuntos) = y(Antiguo,1:NPuntos) - yt(CfTotCt - Cont,1:NPuntos);
if (sum(Dif) ~= 0)||(Antiguo ~= 1)||(Antiguo ~= 34)||(Antiguo ~= 35)
plot (xt(CfTotCt - Cont,1:NPuntos),yt(CfTotCt - Cont,1:NPuntos),'b')
MaxT = round(max(yt(CfTotCt - Cont,1:NPuntos)));
text(xt(CfTotCt - Cont,NPuntos),yt(CfTotCt Cont,NPuntos),horzcat('\rightarrow ','[',num2str(MaxT),' hm^{3}',',',num2str(xt(CfTotCt
- Cont,NPuntos)),'msnm]'));
legend('Volumen Util','Volumen Total','Location','SEO');
else
legend('Volumen Util','Location','SEO');
end
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
123
else
if Cont == 2
PrimerTramo = find(xt(CfTotCt - Cont,1:NPuntos)<VTotal(CfTotCtCont,12));
Union = max(PrimerTramo);
plot (xt(CfTotCt - Cont,1:Union),yt(CfTotCt - Cont,1:Union),'g');
plot (xt(CfTotCt - 1,Union:NPuntos),yt(CfTotCt - 1,Union:NPuntos),'b');
MaxT = round(max(yt(CfTotCt - 1,1:NPuntos)));
text(xt(CfTotCt - 1,NPuntos),yt(CfTotCt 1,NPuntos),horzcat('\rightarrow ','[',num2str(MaxT),' hm^{3}',',',num2str(xt(CfTotCt 1,NPuntos)),'msnm]'));
legend('Volumen Util','Volumen Total1','Volumen
Total2','Location','SEO');
else
plot (xValdecanas,yValdecanas,'b');
legend('VolUtil','VolTotal','Location','SEO');
end
end
NbArchivo = strcat(num2str(Antiguo),'_F1');
saveas(gcf,NbArchivo,'jpeg');
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = CoefTot(CfTotCt,1);
Cont = 0;
end
Cont = Cont + 1;
end
title (Embalses(Antiguo,2),'FontSize',17);
xlabel ('Cota (msnm) ','FontSize',15);
ylabel('Volumen (hm^{3})','FontSize',15);
plot (x(Antiguo,1:NPuntos),y(Antiguo,1:NPuntos),'r','linewidth',2);
Max = max(y(Antiguo,1:NPuntos));
text(x(Antiguo,NPuntos),y(Antiguo,NPuntos),horzcat('\rightarrow ','[',num2str(Max),'
hm^{3}',',',num2str(x(Antiguo,NPuntos)),'msnm]'));
if Cont == 1
plot (xt(CfTotCt - Cont,1:NPuntos),yt(CfTotCt - Cont,1:NPuntos),'g');
MaxT = round(max(yt(CfTotCt - Cont,1:NPuntos)));
text(xt(CfTotCt - Cont,NPuntos),yt(CfTotCt - Cont,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' hm^{3}',',',num2str(xt(CfTotCt - Cont,NPuntos)),'msnm]'));
legend('Volumen Util','Volumen Total','Location','SEO');
else
if Cont == 2
PrimerTramo = find(xt(CfTotCt - 1,1:NPuntos)<VTotal(CfTotCt- 1,12));
Union = max(PrimerTramo);
plot (xt(CfTotCt - 1,1:Union),yt(CfTotCt - 1,1:Union),'g');
plot (xt(CfTotCt,Union:NPuntos),yt(CfTotCt,Union:NPuntos),'k');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' hm^{3}',num2str(xt(CfTotCt,NPuntos)),'msnm]'));
legend('Volumen Util','Volumen Total1','Volumen Total2','Location','SEO');
else
legend('VolTotal1','VolTotal2','VolTotal3','VolUtil');
end
end
NbArchivo = strcat(num2str(Antiguo),'_F1');
saveas(gcf,NbArchivo,'jpeg');
return
Código que realiza el ajuste de la función cota – volumen total para Valdecañas:
%Juan Palomares
%Ajuste de la función cota - volumen total de Valdecañas
%%
function AjusteValdecanas()
%cargo col1=abscisas, col2=ordenadas
load PuntosValdecanas
%%
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
x=PuntosValdecanas(1,:);
y=PuntosValdecanas(2,:);
c = polyfit(x,y,4);
yp = polyval(c,x);
%%
%Dibujo spline encima de función inversa
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
title ('Valdecañas');
xlabel ('Cota');
ylabel('Volumen total');
plot(x,yp,'r');
NbArchivo = strcat('Valde');
saveas(gcf,NbArchivo,'jpeg');
return
C.2
Función que relaciona el caudal total y la cota afterbay
%Autor: Juan Palomares
%Caudal turbinado y vertido - cota de desagüe
%%
function CaudalCotaDesague()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de centrales (col2)
% y sus respectivos índices (col3)
load Centrales
%Cargo CaudalTurbVert: col1=NCurvas, col2 = índice central,
%col3 = índice curvas, col4 = VLIM, col5 = cota embalse aguas abajo,
%col6 = caudal turbinado central paralela y col7 - col10 coef en orden
%[coef0,...,coefn]
load CaudalTurbVert
%Cargo leyenda: primer número es cota embalse aguas abajo y segundo número
% es caudal turbinado por central paralela
load Leyenda
%%
%Número de centrales
NCurvas = length(CaudalTurbVert);
%Número de puntos que pintaré
NPuntos = 1000;
%Matriz de coeficientes
Cambio = 0;
for CfCt =1: NCurvas
%Pongo índices para luego saber cuántas curvas pongo en cada gráfica
if CaudalTurbVert(CfCt,3) == 1
Cambio = Cambio + 1;
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = CaudalTurbVert(CfCt,7:10);
else
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = CaudalTurbVert(CfCt,7:10);
end
end
%Necesito el orden: coefn, coef(n-1),...,coef0] para usar polyval
Coef= fliplr(Coef);
124
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
%Cambio los VLim1 = 10000 por el máximo{VLim2, VLim3, etc.}
%b es un vector con VLIM
b = CaudalTurbVert(:,4);
%a es un vector con las posiciones donde VLIM = 9999
a = find(b > 9998);
%cambio los VLIM = 9999 por 100 (momentáneamente)
b(a) = 100;
for CfCt = 2:NCurvas
%entra en el if cuando he pasado una central con varias curvas
if CaudalTurbVert(CfCt,3) == 1 && CaudalTurbVert(CfCt - 1,3) ~= 1
%número de curvas de la central que he pasado
Cont = CaudalTurbVert(CfCt - 1,3);
%me quedo con el máximo de los VLIM (que no será VLIM = 9999 porque
%ahora vale 100)
Mx = max(b((CfCt - Cont):(CfCt - 1)));
%pongo los VLIM que inicialmente valían 9999 por el siguiente VLIm máx
b((CfCt - Cont):(CfCt - 1)) = Mx;
end
end
%Como CfCt empieza en "2", tengo que comprobar el último
if CaudalTurbVert(CfCt,3)~= 1
Cont = CaudalTurbVert(CfCt,3) - 1;
Mx = max(b((CfCt - Cont):(CfCt - 1)));
b((CfCt - Cont):CfCt) = Mx;
end
CaudalTurbVert(:,4) = b;
%Matriz de abscisas
for CfCt =1: NCurvas
xt(CfCt,1:NPuntos) = linspace(0,CaudalTurbVert(CfCt,4),NPuntos);
end
%Matriz de ordenadas
for CfCt =1: NCurvas
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
%Pinto con el límite matemático máximo (no entro en el if si mis curvas
%son constantes horizontales)
if yt(CfCt,1)~=yt(CfCt,1000)
%b es un vector con las ordenadas de la curva en cuestión
b = yt(CfCt,1:NPuntos);
%yLim es el máximo matemático
yLim = max(b);
%Primer elemento del vector Posic es el máximo matemático
Posic = find(yt(CfCt,1:NPuntos) > yLim - 0.00001);
%Valor de la abscisa con el máximo matemático
xLim = xt(CfCt,Posic(1));
%Vuelvo a pintar 1000 puntos sólo hasta el máximo matemático
xt(CfCt,1:NPuntos) = linspace(0,xLim,NPuntos);
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
%Copio en variable Juanpa xLim que arrastra el filtro cuando VLim era
%10000, e incorpora el filtro de máximo matemático
Juanpa(CfCt,1) = xLim;
end
end
%Gráficas
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = 1;
Cont = 0;
for CfTotCt =1: NCurvas
%Uso índices para saber cuántas curvas pongo en cada gráfica
if Coef(CfTotCt,1) ~= Antiguo
%text('Leyenda = [Cota embalse aguas abajo, Caudal central paralela]');
125
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
126
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal turbinado y vertido total de la central(m^{3}/s)','FontSize',15);
ylabel('Cota de desagüe (msnm)','FontSize',15);
PrimLeyenda = CfTotCt - Cont;
UltLeyenda = CfTotCt - 1;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','NW');
NbArchivo = strcat(num2str(Antiguo),'_F3');
saveas(gcf,NbArchivo,'jpeg');
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = Coef(CfTotCt,1);
Cont = 0;
end
Cont = Cont + 1;
if Cont ==1
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'g','linewidth',2);
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont==2
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'b');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 3
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'k');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 4
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'r');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 5
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'c');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 6
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'m');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxT),' msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 7
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'y');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow ','[',num2str(MaxT),'
msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
if Cont == 8
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'g');
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow ','[',num2str(MaxT),'
msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
else
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'b');
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
127
MaxT = round(max(yt(CfTotCt,1:NPuntos)));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow ','[',num2str(MaxT),'
msnm',',',num2str(xt(CfTotCt,NPuntos)),'m^{3}/s]'));
end
end
end
end
end
end
end
end
end
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal turbinado y vertido total de la central(m^{3}/s)','FontSize',15);
ylabel('Cota de desagüe (msnm)','FontSize',15);
PrimLeyenda = CfTotCt;
UltLeyenda = CfTotCt;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','NW');
NbArchivo = strcat(num2str(Antiguo),'_F3');
saveas(gcf,NbArchivo,'jpeg');
return
C.3
Función que relaciona el caudal unitario y la potencia de generación unitaria
%Autor: Juan Palomares
%Caudal - Potencia generada
%%
function CaudalPotGen()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de centrales (col2)
% y sus respectivos índices (col3)
load Centrales
%Cargo Caudal: col1=NCurvas col2 = índice central, col3 = índice curvas,
%col4 = VLIM, col5 = salto neto, col6 = ruido y col7 - col10 coef en orden
%[coef0,...,coefn]
load Caudal
%Cargo leyenda: número de grupos
load Leyenda
%Cargo coefientes (col2-col4) para hallar caudal máximo para un salto neto
load CoefHnQmax
%%
%Número de centrales
NCurvas = length(Caudal);
%Número de puntos que pintaré
NPuntos = 1000;
%Matriz de coeficientes
Cambio = 0;
for CfCt =1: NCurvas
%Pongo índices para luego saber cuántas curvas pongo en cada gráfica
if Caudal(CfCt,3) == 1
Cambio = Cambio + 1;
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
else
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
end
end
%Necesito el orden: coefn, coef(n-1),...,coef0] para usar polyval
Coef= fliplr(Coef);
%Genero un vector con los caudales máximos para el salto neto al que se
%corresponde cada curva
for CfCt = 1:NCurvas
Qmax(CfCt,1) = polyval(CoefHnQmax(Caudal(CfCt,2),2:4),Caudal(CfCt,5));
end
%Matriz de abscisas
for CfCt =1: NCurvas
xt(CfCt,1:NPuntos) = linspace(0,Qmax(CfCt,1),NPuntos);
end
%Matriz de ordenadas
for CfCt =1: NCurvas
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
%Pinto con Potencia empezando positiva
%b es un vector con las ordenadas de la curva en cuestión
b = yt(CfCt,1:NPuntos);
%Primer elemento del vector PosicMin es donde PLim empieza a ser
%positivo
PosicMin = find(yt(CfCt,1:NPuntos) > 0);
%Valor de la abscisa con PLim positivo
xMin = xt(CfCt,PosicMin(1));
%Vuelvo a pintar 1000 puntos sólo hasta el máximo matemático
xt(CfCt,1:NPuntos) = linspace(xMin,Qmax(CfCt,1),NPuntos);
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
%Copio en variable Juanpa xMin que arrastran los cambios
%hechos a mano y el de ordenada positiva
JuanpaMin(CfCt,1) = xMin;
end
%Gráficas
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = 1;
Cont = 0;
for CfTotCt =1: NCurvas
%Uso índices para saber cuántas curvas pongo en cada gráfica
if Coef(CfTotCt,1) ~= Antiguo
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',15);
ylabel('Potencia generada (MW)','FontSize',15);
PrimLeyenda = CfTotCt - Cont;
UltLeyenda = CfTotCt - 1;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','Best');
NbArchivo = strcat(num2str(Antiguo),'_F7');
saveas(gcf,NbArchivo,'jpeg');
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = Coef(CfTotCt,1);
Cont = 0;
end
Cont = Cont + 1;
if Cont == 1
128
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
129
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'g');
else
if Cont == 2
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'b');
else
if Cont == 3
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'k');
else
if Cont == 4
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'r');
else
if Cont == 5
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'c');
else
if Cont == 6
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'m');
else
if Cont == 7
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'y');
else
if Cont == 8
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'-g');
else
if Cont == 9
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'--b');
else
if Cont == 10
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'--y');
else
if Cont == 11
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'ob');
else
if Cont ==12
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'ok');
else
if Cont ==13
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'or');
else
if Cont ==14
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'oc');
else
if Cont ==15
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'om');
else
if Cont ==16
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'oy');
else
if Cont==17
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'xy');
else
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'xb');
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
end
end
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',15);
ylabel('Potencia generada (MW)','FontSize',15);
PrimLeyenda = CfTotCt - Cont;
UltLeyenda = CfTotCt - 1;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','Best');
NbArchivo = strcat(num2str(Antiguo),'_F7');
saveas(gcf,NbArchivo,'jpeg');
return
C.4
Función que relaciona el salto neto y la potencia unitaria máxima
%Autor: Juan Palomares
%Salto neto - Potencia límite
%%
function SaltoNetoPotLim()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de centrales (col2)
% y sus respectivos índices (col3)
load Centrales
%Cargo SaltoNeto: col1 = índice central, col2 = índice curvas, col3 = VLIM,
%col4 y 5 = ruido, y col6 - 8 coef en orden:%[coef0,...,coefn]
load SaltoNeto
%Col1 = salto neto mínimo que es APROXIMADAMENTE igual a
%cotaminembaa - cotmaxembaab( ó -cota desague si ésta es mayor que cotamaxembaa),
%y salto neto máximo que es APROXIMADAMENTE IGUAL a cotamaxembaa - cotaminembaab
%(ó -cotadesague si ésta es menor que cotaminembaab)
load HnMinMax
%%
%Número de centrales
NCurvas = length(SaltoNeto);
%Número de puntos que pintaré
NPuntos = 1000;
%Matriz de coeficientes
for CfCt =1: NCurvas
%Pongo índices
%(en este caso
Coef(CfCt,4) =
Coef(CfCt,1:3)
para luego saber cuántas curvas pongo en cada gráfica
será una)
CfCt;
= SaltoNeto(CfCt,6:8);
end
%Necesito el orden: coefn, coef(n-1),...,coef0] para usar polyval
Coef= fliplr(Coef);
%%
%Matriz de abscisas
for CfCt =1: NCurvas
xt(CfCt,1:NPuntos) = linspace(HnMinMax(CfCt,1),HnMinMax(CfCt,2),NPuntos);
end
%Matriz de ordenadas
130
C Control analítico y gráfico de las características hidroeléctricas mediante programación en Matlab
for CfCt =1: NCurvas
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:4),xt(CfCt,1:NPuntos));
%Pinto con PLim empezando positiva y llegando a límite matemático máximo (no entro
en el if si mis curvas
%son constantes horizontales)
if yt(CfCt,1)~=yt(CfCt,1000)
%b es un vector con las ordenadas de la curva en cuestión
b = yt(CfCt,1:NPuntos);
%yLim es el máximo matemático
yLim = max(b);
%Primer elemento del vector PosicMax es el máximo matemático
PosicMax = find(yt(CfCt,1:NPuntos) > yLim - 0.00001);
%Valor de la abscisa con el máximo matemático
xLim = xt(CfCt,PosicMax(1));
%Primer elemento del vector PosicMin es donde PLim empieza a ser
%positivo
PosicMin = find(yt(CfCt,1:NPuntos) > 0);
%Valor de la abscisa con PLim positivo
if CfCt == 44
%Urdiceto no vale
xMin = 1;
else
xMin = xt(CfCt,PosicMin(1));
end
%Vuelvo a pintar 1000 puntos sólo hasta el máximo matemático
xt(CfCt,1:NPuntos) = linspace(xMin,xLim,NPuntos);
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:4),xt(CfCt,1:NPuntos));
%Copio en variable Juanpa xMin y xLim que arrastran los cambios
%hechos a mano sobre el .m, el filtro de máximo matemático y el de
%ordenada positiva
JuanpaMin(CfCt,1) = xMin;
JuanpaMax(CfCt,1) = xLim;
end
end
%Gráficas
for CfTotCt =1: NCurvas
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
title (Centrales(CfTotCt,2),'FontSize',17);
xlabel ('Salto neto (m)','FontSize',15);
ylabel('Potencia máxima por grupo(MW)','FontSize',15);
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'g','linewidth',2);
if yt(CfTotCt,1)~=yt(CfTotCt,1000)
MaxY = max(yt(CfTotCt,1:NPuntos));
MinY = min(yt(CfTotCt,1:NPuntos));
%Si central es muy pequeña (Chandreja 1, Chandreja 2, Guístolas y Puentelarra)
mejor no redondeo
if MaxY > 3
MaxY = round(max(yt(CfTotCt,1:NPuntos)));
MinY = round(min(yt(CfTotCt,1:NPuntos)));
end
MaxX = round(xt(CfTotCt,NPuntos));
MinX = round(xt(CfTotCt,1));
text(xt(CfTotCt,NPuntos),yt(CfTotCt,NPuntos),horzcat('\rightarrow
','[',num2str(MaxY),' MW',',',num2str(MaxX),'m]'));
text(xt(CfTotCt,1),yt(CfTotCt,1),horzcat('\rightarrow ','[',num2str(MinY),'
MW',',',num2str(MinX),'m]'));
end
NbArchivo = strcat(num2str(CfTotCt),'_F5');
saveas(gcf,NbArchivo,'jpeg');
end
return
131
D
Desarrollo de interfaces y
realización de cálculos en Excel
mediante programación en VBA
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
133
D Desarrollo de interfaces y realización de cálculos en Excel
mediante programación en VBA
D.1
Declaraciones
'DECLARACIONES DE LA ESTRUCTURA DE LA CENTRAL
'Tipo usado para las características de la base de datos generales
Public Type CentralGral
Nb As String
Cuenca As String
Comdad As String
Prov As String
Munic As String
Rio As String
Superf As String
Tipo As String
TipoTurb As String
DesdeT As String
HaciaT As String
DesdeB As String
HaciaB As String
NGrGen As Integer
NGrBmb As Integer
'Las variables de tipo Variant se deben a que puede que tengan su campo vacio
Aport As Variant
QMed As Variant
Precip As Variant
PotInst As Variant
PotMxTot As Double
PotMxUnit As Double
QMxTot As Double
QMxUnit As Double
PMxTotBmb As Double
PMxUnitBmb As Double
QMxTotBmb As Double
QMxUnitBmb As Double
CMinAa As Double
CMaxAa As Double
CMinAab As Double
CMaxAab As Double
CDes As Double
End Type
'Tipo usado para las características de las funciones
Public Type CaractFuncion
Nb() As String
Curva() As Integer
c0() As Variant
c1() As Variant
c2() As Variant
c3() As Variant
Cor1() As Variant
Cor2() As Variant
VMin() As Variant
VMax() As Variant
End Type
'Tipo usado para copiar todo
Public Type Ctr
Gral As CentralGral
Fc As CaractFuncion
End Type
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
'DECLARACIONES DE LA ESTRUCTURA DEL EMBALSE
'Tipo usado para las características de la base de datos generales
Public Type EmbalseGral
Nb As String
Cuenca As String
Comdad As String
Prov As String
Munic As String
Rio As String
Superf As String
Ppales As String
Asoc As String
Trasv As String
Tipo As String
'Las variables de tipo Variant se deben a que puede que tengan su campo vacio
AportMedia As Variant
QMedio As Variant
PrecipMedia As Variant
SuperfInund As Variant
VolNor As Variant
Long As Variant
Cim As Variant
Coronac As Variant
NComp As Variant
NAlivSup As Variant
QMaxAlivSup As Variant
NDesFondo As Variant
QMaxDesFondo As Variant
Riegos As Variant
LimProd As Variant
LimEvac As Variant
Aforos As Variant
CotaMinNor As Variant
CotaMinExtraord As Variant
CotaMaxNor As Variant
CotaMaxExtraord As Variant
CotaRiegos As Variant
CotaAvenidas As Variant
VolUtilMax As Variant
VolTotMax As Variant
End Type
'Tipo usado para las características de las funciones
Public Type CaractEmb
Nb() As String
Curva() As Integer
c0() As Variant
c1() As Variant
c2() As Variant
c3() As Variant
c4() As Variant
VMin() As Variant
VMax() As Variant
VRef() As Variant
RgVTot() As Variant
End Type
'Tipo usado para copiar todo
Public Type Emb
Gral As EmbalseGral
Fc As CaractEmb
End Type
D.2
Búsqueda del embalse o central
Sub BuscaCentral(ByVal NombreCentral As String, ByRef IndCentral As Integer)
134
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
135
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
'Busco central y copio su índice en variable IndCentral
ActiveWorkbook.Sheets("Base de datos centrales").Select
[B:B].Find(NombreCentral).Offset(0, -1).Activate 'El nombre de la central está
siempre en la columna B
IndCentral = ActiveCell.Value
Application.ScreenUpdating = True
End Sub
Sub BuscaEmbalse(ByVal NombreEmbalse As String, ByRef IndEmbalse As Integer)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
'Busco central y copio su índice en variable IndCentral
ActiveWorkbook.Sheets("Base de datos embalses").Select
[B:B].Find(NombreEmbalse).Offset(0, -1).Activate 'El nombre del embalse está siempre
en la columna B
IndEmbalse = ActiveCell.Value
Application.ScreenUpdating = True
End Sub
D.3
Llenado de las estructuras de VBA correspondientes al embalse o central
Sub RellenaCentral(ByVal IndCentral As Integer, ByRef Central As Ctr)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
Dim Cont As Integer
Dim NFilasAdicionales As Integer
Dim NRellena As Integer
Const NHojasCentrales = 8 'Hay 8 funciones de características de centrales
Dim HojasCentrales(1 To NHojasCentrales) As String
'Introduzco las características de base de datos generales
Central.Gral.Nb = ActiveCell.Offset(0, 1).Value
Central.Gral.Cuenca = ActiveCell.Offset(0, 2).Value
Central.Gral.Comdad = ActiveCell.Offset(0, 3).Value
Central.Gral.Prov = ActiveCell.Offset(0, 4).Value
Central.Gral.Munic = ActiveCell.Offset(0, 5).Value
Central.Gral.Rio = ActiveCell.Offset(0, 6).Value
Central.Gral.Superf = ActiveCell.Offset(0, 7).Value
Central.Gral.Tipo = ActiveCell.Offset(0, 11).Value
Central.Gral.TipoTurb = ActiveCell.Offset(0, 14).Value
Central.Gral.DesdeT = ActiveCell.Offset(0, 29).Value
Central.Gral.HaciaT = ActiveCell.Offset(0, 30).Value
Central.Gral.DesdeB = ActiveCell.Offset(0, 31).Value
Central.Gral.HaciaB = ActiveCell.Offset(0, 32).Value
Central.Gral.NGrGen = ActiveCell.Offset(0, 33).Value
Central.Gral.NGrBmb = ActiveCell.Offset(0, 13).Value
Central.Gral.Aport = ActiveCell.Offset(0, 8).Value
Central.Gral.QMed = ActiveCell.Offset(0, 9).Value
Central.Gral.Precip = ActiveCell.Offset(0, 10).Value
Central.Gral.PotInst = ActiveCell.Offset(0, 15).Value
Central.Gral.PotMxTot = ActiveCell.Offset(0, 16).Value
Central.Gral.PotMxUnit = ActiveCell.Offset(0, 17).Value
Central.Gral.QMxTot = ActiveCell.Offset(0, 18).Value
Central.Gral.QMxUnit = ActiveCell.Offset(0, 19).Value
Central.Gral.PMxTotBmb = ActiveCell.Offset(0, 20).Value
Central.Gral.PMxUnitBmb = ActiveCell.Offset(0, 21).Value
Central.Gral.QMxTotBmb = ActiveCell.Offset(0, 22).Value
Central.Gral.QMxUnitBmb = ActiveCell.Offset(0, 23).Value
Central.Gral.CMinAa = ActiveCell.Offset(0, 24).Value
Central.Gral.CMaxAa = ActiveCell.Offset(0, 25).Value
Central.Gral.CMinAab = ActiveCell.Offset(0, 26).Value
Central.Gral.CMaxAab = ActiveCell.Offset(0, 27).Value
Central.Gral.CDes = ActiveCell.Offset(0, 28).Value
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
'Vector que apunta a diferentes hojas
HojasCentrales(1) = "F3"
HojasCentrales(2) = "F4"
HojasCentrales(3) = "F5"
HojasCentrales(4) = "F6"
HojasCentrales(5) = "F7"
HojasCentrales(6) = "F8"
HojasCentrales(7) = "F9"
HojasCentrales(8) = "F10"
'Inicializaciones
NCurvas = 0
'Introduzco las características de las funciones
For Cont = 1 To NHojasCentrales
ActiveWorkbook.Sheets(HojasCentrales(Cont)).Select
[B:B].Find(IndCentral).Activate 'El índice central siempre está en columna B
ActiveCell.Select
NRellena = 0
'Relleno con las características de la función (incluyendo los "Dummy")
While ActiveCell.Offset(NRellena, 0) = IndCentral
Central.Fc.Nb(NCurvas + 1) = ActiveCell.Offset(NRellena, -1).Value
Central.Fc.Curva(NCurvas + 1) = NRellena + 1
Central.Fc.c0(NCurvas + 1) = ActiveCell.Offset(NRellena, 2).Value
Central.Fc.c1(NCurvas + 1) = ActiveCell.Offset(NRellena, 3).Value
Central.Fc.c2(NCurvas + 1) = ActiveCell.Offset(NRellena, 4).Value
Central.Fc.c3(NCurvas + 1) = ActiveCell.Offset(NRellena, 5).Value
Central.Fc.Cor1(NCurvas + 1) = ActiveCell.Offset(NRellena, 6).Value
Central.Fc.Cor2(NCurvas + 1) = ActiveCell.Offset(NRellena, 7).Value
Central.Fc.VMin(NCurvas + 1) = ActiveCell.Offset(NRellena, 8).Value
Central.Fc.VMax(NCurvas + 1) = ActiveCell.Offset(NRellena, 9).Value
NCurvas = NCurvas + 1
NRellena = NRellena + 1
Wend
Next Cont
Application.ScreenUpdating = True
End Sub
Sub RellenaEmbalse(ByVal IndEmbalse As Integer, ByRef Embalse As Emb)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
Dim Cont As Integer
Dim NFilasAdicionales As Integer
Dim NRellena As Integer
Const NHojasEmbalses = 3 'Hay 3 funciones de características de embalses
Dim HojasEmbalses(1 To NHojasEmbalses) As String
'Introduzco las características de base de datos generales
Embalse.Gral.Nb = ActiveCell.Offset(0, 1).Value
Embalse.Gral.Cuenca = ActiveCell.Offset(0, 2).Value
Embalse.Gral.Comdad = ActiveCell.Offset(0, 3).Value
Embalse.Gral.Prov = ActiveCell.Offset(0, 4).Value
Embalse.Gral.Munic = ActiveCell.Offset(0, 5).Value
Embalse.Gral.Rio = ActiveCell.Offset(0, 6).Value
Embalse.Gral.Superf = ActiveCell.Offset(0, 7).Value
Embalse.Gral.AportMedia = ActiveCell.Offset(0, 8).Value
Embalse.Gral.QMedio = ActiveCell.Offset(0, 9).Value
Embalse.Gral.PrecipMedia = ActiveCell.Offset(0, 10).Value
Embalse.Gral.SuperfInund = ActiveCell.Offset(0, 11).Value
Embalse.Gral.VolNor = ActiveCell.Offset(0, 12).Value
Embalse.Gral.Long = ActiveCell.Offset(0, 13).Value
Embalse.Gral.Ppales = ActiveCell.Offset(0, 14).Value
Embalse.Gral.Asoc = ActiveCell.Offset(0, 15).Value
136
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Embalse.Gral.Trasv = ActiveCell.Offset(0, 16).Value
Embalse.Gral.Tipo = ActiveCell.Offset(0, 17).Value
Embalse.Gral.Cim = ActiveCell.Offset(0, 18).Value
Embalse.Gral.Coronac = ActiveCell.Offset(0, 19).Value
Embalse.Gral.NComp = ActiveCell.Offset(0, 20).Value
Embalse.Gral.NAlivSup = ActiveCell.Offset(0, 21).Value
Embalse.Gral.QMaxAlivSup = ActiveCell.Offset(0, 22).Value
Embalse.Gral.NDesFondo = ActiveCell.Offset(0, 23).Value
Embalse.Gral.QMaxDesFondo = ActiveCell.Offset(0, 24).Value
Embalse.Gral.Riegos = ActiveCell.Offset(0, 25).Value
Embalse.Gral.LimProd = ActiveCell.Offset(0, 26).Value
Embalse.Gral.LimEvac = ActiveCell.Offset(0, 27).Value
Embalse.Gral.Aforos = ActiveCell.Offset(0, 28).Value
Embalse.Gral.CotaMinNor = ActiveCell.Offset(0, 29).Value
Embalse.Gral.CotaMinExtraord = ActiveCell.Offset(0, 30).Value
Embalse.Gral.CotaMaxNor = ActiveCell.Offset(0, 31).Value
Embalse.Gral.CotaMaxExtraord = ActiveCell.Offset(0, 32).Value
Embalse.Gral.CotaRiegos = ActiveCell.Offset(0, 33).Value
Embalse.Gral.CotaAvenidas = ActiveCell.Offset(0, 34).Value
Embalse.Gral.VolUtilMax = ActiveCell.Offset(0, 35).Value
Embalse.Gral.VolTotMax = ActiveCell.Offset(0, 36).Value
'Vector que apunta
HojasEmbalses(1) =
HojasEmbalses(2) =
HojasEmbalses(3) =
a diferentes hojas
"F1"
"F2"
"Inversa F1"
'Inicializaciones
NCurvas = 0
'Introduzco las características de las funciones
For Cont = 1 To NHojasEmbalses
ActiveWorkbook.Sheets(HojasEmbalses(Cont)).Select
[B:B].Find(IndEmbalse).Activate 'El índice Embalse siempre está en columna B
ActiveCell.Select
NRellena = 0
'Relleno con las características de la función (incluyendo los "Dummy")
While ActiveCell.Offset(NRellena, 0) = IndEmbalse
Embalse.Fc.Nb(NCurvas + 1) = ActiveCell.Offset(NRellena, -1).Value
Embalse.Fc.Curva(NCurvas + 1) = NRellena + 1
Embalse.Fc.c0(NCurvas + 1) = ActiveCell.Offset(NRellena, 2).Value
Embalse.Fc.c1(NCurvas + 1) = ActiveCell.Offset(NRellena, 3).Value
Embalse.Fc.c2(NCurvas + 1) = ActiveCell.Offset(NRellena, 4).Value
Embalse.Fc.c3(NCurvas + 1) = ActiveCell.Offset(NRellena, 5).Value
Embalse.Fc.c4(NCurvas + 1) = ActiveCell.Offset(NRellena, 6).Value
Embalse.Fc.VMin(NCurvas + 1) = ActiveCell.Offset(NRellena, 7).Value
Embalse.Fc.VMax(NCurvas + 1) = ActiveCell.Offset(NRellena, 8).Value
Embalse.Fc.VRef(NCurvas + 1) = ActiveCell.Offset(NRellena, 9).Value
Embalse.Fc.RgVTot(NCurvas + 1) = ActiveCell.Offset(NRellena, 10).Value
NCurvas = NCurvas + 1
NRellena = NRellena + 1
Wend
Next Cont
Application.ScreenUpdating = True
End Sub
D.4
Carga de características del embalse o central
Sub CargaCentral(ByRef Central As Ctr)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
'Borro la central anterior
Call BorraParaCargarNueva
Dim ContCarga As Integer 'Contador que cuenta el número total ristras
Dim ContCargaFc As Integer 'Contador que cuenta las ristras de cada función
137
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim ContFc As Integer 'Contador que cuenta el número de funciones
Const NumFc = 8 'Hay 8 funciones de características de centrales
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
MinCor1 As Variant
MinCor2 As Variant
MinVMin As Variant
MaxCor1 As Variant
MaxCor2 As Variant
MaxVMax As Variant
QTurbVerMin As Variant
QTurbVerMax As Variant
Dim DistFc(1 To NumFc) As String
Dim CeldaAsocFc(1 To NumFc) As Integer
Dim CeldaAsocCalc(1 To NumFc) As Integer
'Relleno todos los campos del libro Datos central
ActiveWorkbook.Sheets("Datos central").Select
Cells(1, 1).Value = Central.Gral.Nb
Cells(12, 2).Value = Central.Gral.Comdad
Cells(13, 2).Value = Central.Gral.Prov
Cells(14, 2).Value = Central.Gral.Munic
Cells(15, 2).Value = Central.Gral.Cuenca
Cells(16, 2).Value = Central.Gral.Rio
Cells(12, 4).Value = Central.Gral.Superf
Cells(13, 4).Value = Central.Gral.Aport
Cells(14, 4).Value = Central.Gral.QMed
Cells(15, 4).Value = Central.Gral.Precip
Cells(12, 6).Value = Central.Gral.DesdeT
Cells(13, 6).Value = Central.Gral.HaciaT
Cells(14, 6).Value = Central.Gral.DesdeB
Cells(15, 6).Value = Central.Gral.HaciaB
Cells(24, 2).Value = Central.Gral.Tipo
Cells(25, 2).Value = Central.Gral.NGrGen
Cells(26, 2).Value = Central.Gral.NGrBmb
Cells(27, 2).Value = Central.Gral.TipoTurb
Cells(28, 2).Value = Central.Gral.PotInst
Cells(29, 2).Value = Central.Gral.CDes
Cells(24, 4).Value = Central.Gral.PotMxTot
Cells(25, 4).Value = Central.Gral.PotMxUnit
Cells(26, 4).Value = Central.Gral.QMxTot
Cells(27, 4).Value = Central.Gral.QMxUnit
Cells(24, 6).Value = Central.Gral.PMxTotBmb
Cells(25, 6).Value = Central.Gral.PMxUnitBmb
Cells(26, 6).Value = Central.Gral.QMxTotBmb
Cells(27, 6).Value = Central.Gral.QMxUnitBmb
'Relleno tabla de características para una condición de funcionamiento
Cells(241, 2).Value = Central.Gral.CMinAa
Cells(241, 3).Value = Central.Gral.CMaxAa
Cells(242, 2).Value = Central.Gral.CMinAab
Cells(242, 3).Value = Central.Gral.CMaxAab
'Vector que apunta a diferentes funciones
DistFc(1) = "F3"
DistFc(2) = "F4"
DistFc(3) = "F5"
DistFc(4) = "F6"
DistFc(5) = "F7"
DistFc(6) = "F8"
DistFc(7) = "F9"
DistFc(8) = "F10"
'Vector que apunta a diferentes celdas de tablas funciones
CeldaAsocFc(1) = 43
CeldaAsocFc(2) = 57
CeldaAsocFc(3) = 68
CeldaAsocFc(4) = 75
CeldaAsocFc(5) = 82
CeldaAsocFc(6) = 97
CeldaAsocFc(7) = 115
CeldaAsocFc(8) = 138
ContCarga = 1
ContCargaFc = 1
'Relleno tablas de funciones
138
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
For ContFc = 1 To NumFc
ContCarga = 1
While Central.Fc.Nb(ContCargaFc) = DistFc(ContFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.Curva(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.c0(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.c1(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.c2(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.c3(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.Cor1(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.Cor2(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.VMin(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Central.Fc.VMax(ContCargaFc)
+ ContCarga - 1, 1).Value =
+ ContCarga - 1, 2).Value =
+ ContCarga - 1, 3).Value =
+ ContCarga - 1, 4).Value =
+ ContCarga - 1, 5).Value =
+ ContCarga - 1, 6).Value =
+ ContCarga - 1, 7).Value =
+ ContCarga - 1, 8).Value =
+ ContCarga - 1, 9).Value =
ContCarga = ContCarga + 1
ContCargaFc = ContCargaFc + 1
Wend
Next ContFc
'Vector que apunta
CeldaAsocCalc(1) =
CeldaAsocCalc(2) =
CeldaAsocCalc(3) =
CeldaAsocCalc(4) =
CeldaAsocCalc(5) =
CeldaAsocCalc(6) =
CeldaAsocCalc(7) =
CeldaAsocCalc(8) =
a diferentes celdas de tablas cálculos
167
175
182
188
194
201
211
218
ContCargaFc = 1
MinCor1 = 99999
MaxCor1 = -9999
MinCor2 = 99999
MaxCor2 = -9999
MinVMin = 99999
MaxVMax = -9999
'Relleno tablas de cálculos
For ContFc = 1 To NumFc
While Central.Fc.Nb(ContCargaFc) = DistFc(ContFc)
'Hallo valor mínimos y máximos de entre todos los valores de cortes de
función y de abscisas
If Central.Fc.Cor1(ContCargaFc) < MinCor1 Then
MinCor1 = Central.Fc.Cor1(ContCargaFc)
End If
If Central.Fc.Cor1(ContCargaFc) > MaxCor1 Then
MaxCor1 = Central.Fc.Cor1(ContCargaFc)
End If
If Central.Fc.Cor2(ContCargaFc) < MinCor2 Then
MinCor2 = Central.Fc.Cor2(ContCargaFc)
End If
If Central.Fc.Cor2(ContCargaFc) > MaxCor2 Then
MaxCor2 = Central.Fc.Cor2(ContCargaFc)
End If
If Central.Fc.VMin(ContCargaFc) < MinVMin Then
MinVMin = Central.Fc.VMin(ContCargaFc)
End If
If Central.Fc.VMax(ContCargaFc) > MaxVMax Then
MaxVMax = Central.Fc.VMax(ContCargaFc)
139
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
End If
ContCargaFc = ContCargaFc + 1
Wend
Cells(CeldaAsocCalc(ContFc), 2).Value = MinVMin
Cells(CeldaAsocCalc(ContFc), 3).Value = MaxVMax
Cells(CeldaAsocCalc(ContFc) + 1, 2).Value = MinCor1
Cells(CeldaAsocCalc(ContFc) + 1, 3).Value = MaxCor1
Cells(CeldaAsocCalc(ContFc) + 2, 2).Value = MinCor2
Cells(CeldaAsocCalc(ContFc) + 2, 3).Value = MaxCor2
'Relleno tabla colinas de rendimiento (con datos de F7-->ContFc = 5)
If ContFc = 5 Then
Cells(228, 2) = MinVMin
Cells(228, 3) = MaxVMax
Cells(229, 2) = MinCor1
Cells(229, 3) = MaxCor1
End If
'Relleno la tabla de características para una condición de funcionamiento
If ContFc = 1 Then '(con datos de F3-->ContFc = 1)
Cells(243, 2) = MinCor2
Cells(243, 3) = MaxCor2
QTurbVerMin = MinVMin
QTurbVerMax = MaxVMax
End If
If ContFc = 2 Then '(con datos de F4-->ContFc = 2, y de F3 guardados en
variables QTurbVer)
Cells(240, 2) = QTurbVerMin - MinVMin
Cells(240, 3) = QTurbVerMax - MaxVMax
Cells(244, 2) = MinCor1
Cells(244, 3) = MaxCor1
End If
If ContFc = 6 Then '(con datos de F8-->ContFc = 6)
Cells(239, 2) = MinVMin
Cells(239, 3) = MaxVMax
End If
MinCor1
MaxCor1
MinCor2
MaxCor2
MinVMin
MaxVMax
=
=
=
=
=
=
99999
-9999
99999
-9999
99999
-9999
Next ContFc
'Borro los dummys y ajusto los espacios que deja en blanco
Call BorraDummys
'Muevo cursor hasta arriba del todo
Cells(1, 1).Activate
ActiveWindow.ScrollRow = 7
ActiveWorkbook.Sheets("Datos central").Activate
Application.ScreenUpdating = True
End Sub
Sub CargaEmbalse(ByRef Embalse As Emb)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
'Borro el embalse anterior
Call BorraParaCargarNuevo
Dim ContCarga As Integer 'Contador que cuenta el número total ristras
Dim ContCargaFc As Integer 'Contador que cuenta las ristras de cada función
Dim ContFc As Integer 'Contador que cuenta el número de funciones
Const NumFc = 3 'Hay 3 funciones de características de embalses
140
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim DistFc(1 To NumFc) As String
Dim CeldaAsocFc(1 To NumFc) As Integer
Dim CeldaAsocCalc(1 To NumFc) As Integer
'Relleno todos los campos del libro Datos central
ActiveWorkbook.Sheets("Datos embalse").Select
Cells(1, 1).Value = Embalse.Gral.Nb
Cells(11, 2).Value = Embalse.Gral.Comdad
Cells(12, 2).Value = Embalse.Gral.Prov
Cells(13, 2).Value = Embalse.Gral.Munic
Cells(14, 2).Value = Embalse.Gral.Cuenca
Cells(15, 2).Value = Embalse.Gral.Rio
Cells(11, 4).Value = Embalse.Gral.Superf
Cells(12, 4).Value = Embalse.Gral.AportMedia
Cells(13, 4).Value = Embalse.Gral.QMedio
Cells(14, 4).Value = Embalse.Gral.PrecipMedia
Cells(11, 6).Value = Embalse.Gral.SuperfInund
Cells(12, 6).Value = Embalse.Gral.VolNor
Cells(13, 6).Value = Embalse.Gral.Long
Cells(11, 8).Value = Embalse.Gral.Ppales
Cells(12, 8).Value = Embalse.Gral.Asoc
Cells(13, 8).Value = Embalse.Gral.Trasv
Cells(20, 2).Value = Embalse.Gral.Tipo
Cells(21, 2).Value = Embalse.Gral.Cim
Cells(22, 2).Value = Embalse.Gral.Coronac
Cells(23, 2).Value = Embalse.Gral.NComp
Cells(20, 4).Value = Embalse.Gral.NAlivSup
Cells(21, 4).Value = Embalse.Gral.QMaxAlivSup
Cells(22, 4).Value = Embalse.Gral.NDesFondo
Cells(23, 4).Value = Embalse.Gral.QMaxDesFondo
Cells(20, 6).Value = Embalse.Gral.Riegos
Cells(21, 6).Value = Embalse.Gral.LimProd
Cells(22, 6).Value = Embalse.Gral.LimEvac
Cells(23, 6).Value = Embalse.Gral.Aforos
Cells(29, 3).Value = Embalse.Gral.CotaMinNor
Cells(30, 3).Value = Embalse.Gral.CotaMinExtraord
Cells(31, 3).Value = Embalse.Gral.CotaMaxNor
Cells(32, 3).Value = Embalse.Gral.CotaMaxExtraord
Cells(33, 3).Value = Embalse.Gral.CotaRiegos
Cells(34, 3).Value = Embalse.Gral.CotaAvenidas
Cells(29, 5).Value = Embalse.Gral.VolUtilMax
Cells(30, 5).Value = Embalse.Gral.VolTotMax
'Vector que apunta a diferentes funciones
DistFc(1) = "F1"
DistFc(2) = "F2"
DistFc(3) = "F1Inv"
'Vector que apunta a diferentes celdas de tablas funciones
CeldaAsocFc(1) = 44
CeldaAsocFc(2) = 50
CeldaAsocFc(3) = 59
ContCarga = 1
ContCargaFc = 1
'Relleno tablas de funciones
For ContFc = 1 To NumFc
ContCarga = 1
While Embalse.Fc.Nb(ContCargaFc) = DistFc(ContFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.Curva(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.c0(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.c1(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.c2(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.c3(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.c4(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.VMin(ContCargaFc)
Cells(CeldaAsocFc(ContFc)
Embalse.Fc.VMax(ContCargaFc)
+ ContCarga - 1, 1).Value =
+ ContCarga - 1, 2).Value =
+ ContCarga - 1, 3).Value =
+ ContCarga - 1, 4).Value =
+ ContCarga - 1, 5).Value =
+ ContCarga - 1, 6).Value =
+ ContCarga - 1, 7).Value =
+ ContCarga - 1, 8).Value =
141
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Cells(CeldaAsocFc(ContFc) + ContCarga - 1, 9).Value =
Embalse.Fc.VRef(ContCargaFc)
Cells(CeldaAsocFc(ContFc) + ContCarga - 1, 10).Value =
Embalse.Fc.RgVTot(ContCargaFc)
ContCarga = ContCarga + 1
ContCargaFc = ContCargaFc + 1
Wend
Next ContFc
'Vector que apunta
CeldaAsocCalc(1) =
CeldaAsocCalc(2) =
CeldaAsocCalc(3) =
a diferentes celdas de tablas cálculos
81
87
93
'Relleno tablas de cálculos
For ContFc = 1 To NumFc
If ContFc = 1 Then
ContCargaFc = 1
Else
If ContFc = 2 Then
ContCargaFc = 2
Else 'Para ContFc = 3 quiero rango de Inv F1; valdrá con 3 si sólo hay un
tramo de F2, y con 4 si hay dos tramos de F2
If Embalse.Fc.VMin(2) = Embalse.Fc.VMin(3) Then 'Hay dos tramos
ContCargaFc = 4
Else 'Hay un tramo de F2
ContCargaFc = 3
End If
End If
End If
Cells(CeldaAsocCalc(ContFc), 1).Value = Embalse.Fc.VMin(ContCargaFc)
Cells(CeldaAsocCalc(ContFc), 2).Value = Embalse.Fc.VMax(ContCargaFc)
Next ContFc
'Borro los dummys y ajusto los espacios que deja en blanco
Call BorraDummysEmbalse
'Muevo cursor hasta arriba del todo
Cells(1, 1).Activate
ActiveWindow.ScrollRow = 6
ActiveWorkbook.Sheets("Datos embalse").Activate
Application.ScreenUpdating = True
End Sub
D.5
Subrutinas correspondientes a las funciones del embalse
Private Sub ComCotaVTot_Click()
Dim NombreEmbalse As String
Dim Abscisa As Variant
Dim Ordenada As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim IndEmbalse As Integer
Dim Embalse As Emb
ReDim Embalse.Fc.Nb(1 To NMaxCurvas)
ReDim Embalse.Fc.Curva(1 To NMaxCurvas)
ReDim Embalse.Fc.c0(1 To NMaxCurvas)
ReDim Embalse.Fc.c1(1 To NMaxCurvas)
ReDim Embalse.Fc.c2(1 To NMaxCurvas)
ReDim Embalse.Fc.c3(1 To NMaxCurvas)
ReDim Embalse.Fc.c4(1 To NMaxCurvas)
ReDim Embalse.Fc.VMin(1 To NMaxCurvas)
ReDim Embalse.Fc.VMax(1 To NMaxCurvas)
142
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
143
ReDim Embalse.Fc.VRef(1 To NMaxCurvas)
ReDim Embalse.Fc.RgVTot(1 To NMaxCurvas)
NombreEmbalse = Cells(1, 1).Value
'Necesito índice del embalse
Call BuscaEmbalse(NombreEmbalse, IndEmbalse)
'Relleno en estructura "Embalse" con todos los datos del embalse
Call RellenaEmbalse(IndEmbalse, Embalse)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(87, 3)) = False Then
If Cells(87, 3).Value < Cells(87, 1).Value Then
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir una cota mayor que el valor mínimo", vbExclamation,
"CARHI"
Cells(87, 3).Activate
Exit Sub
Else
If Cells(87, 3).Value > Cells(87, 2).Value Then
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir una cota menor que el valor máximo",
vbExclamation, "CARHI"
Cells(87, 3).Activate
Exit Sub
Else
Abscisa = Cells(87, 3).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir la cota", vbExclamation, "CARHI"
Cells(87, 3).Activate
Exit Sub
End If
Call ResultadoFcCotaVTot(Embalse, Abscisa, Ordenada)
Cells(87, 4).Value = Ordenada
ActiveWorkbook.Sheets("Datos embalse").Activate
Cells(87, 4).Activate
End Sub
Private Sub ComCotaVUt_Click()
Dim NombreEmbalse As String
Dim Abscisa As Variant
Dim Ordenada As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndEmbalse As Integer
Dim Embalse As Emb
ReDim Embalse.Fc.Nb(1 To NMaxCurvas)
ReDim Embalse.Fc.Curva(1 To NMaxCurvas)
ReDim Embalse.Fc.c0(1 To NMaxCurvas)
ReDim Embalse.Fc.c1(1 To NMaxCurvas)
ReDim Embalse.Fc.c2(1 To NMaxCurvas)
ReDim Embalse.Fc.c3(1 To NMaxCurvas)
ReDim Embalse.Fc.c4(1 To NMaxCurvas)
ReDim Embalse.Fc.VMin(1 To NMaxCurvas)
ReDim Embalse.Fc.VMax(1 To NMaxCurvas)
ReDim Embalse.Fc.VRef(1 To NMaxCurvas)
ReDim Embalse.Fc.RgVTot(1 To NMaxCurvas)
NombreEmbalse = Cells(1, 1).Value
'Necesito índice del embalse
Call BuscaEmbalse(NombreEmbalse, IndEmbalse)
'Relleno en estructura "Embalse" con todos los datos del embalse
Call RellenaEmbalse(IndEmbalse, Embalse)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(81, 3)) = False Then
If Cells(81, 3).Value < Cells(81, 1).Value Then
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
144
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir una cota mayor que el valor mínimo", vbExclamation,
"CARHI"
Cells(81, 3).Activate
Exit Sub
Else
If Cells(81, 3).Value > Cells(81, 2).Value Then
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir una cota menor que el valor máximo",
vbExclamation, "CARHI"
Cells(81, 3).Activate
Exit Sub
Else
Abscisa = Cells(81, 3).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir la cota", vbExclamation, "CARHI"
Cells(81, 3).Activate
Exit Sub
End If
Call ResultadoFcCotaVUt(Embalse, Abscisa, Ordenada)
Cells(81, 4).Value = Ordenada
ActiveWorkbook.Sheets("Datos embalse").Activate
Cells(81, 4).Activate
End Sub
Private Sub ComVUtCota_Click()
Dim NombreEmbalse As String
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim Tramo As Integer
Dim LimAplic As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndEmbalse As Integer
Dim Embalse As Emb
ReDim Embalse.Fc.Nb(1 To NMaxCurvas)
ReDim Embalse.Fc.Curva(1 To NMaxCurvas)
ReDim Embalse.Fc.c0(1 To NMaxCurvas)
ReDim Embalse.Fc.c1(1 To NMaxCurvas)
ReDim Embalse.Fc.c2(1 To NMaxCurvas)
ReDim Embalse.Fc.c3(1 To NMaxCurvas)
ReDim Embalse.Fc.c4(1 To NMaxCurvas)
ReDim Embalse.Fc.VMin(1 To NMaxCurvas)
ReDim Embalse.Fc.VMax(1 To NMaxCurvas)
ReDim Embalse.Fc.VRef(1 To NMaxCurvas)
ReDim Embalse.Fc.RgVTot(1 To NMaxCurvas)
NombreEmbalse = Cells(1, 1).Value
'Necesito índice del embalse
Call BuscaEmbalse(NombreEmbalse, IndEmbalse)
'Relleno en estructura "Embalse" con todos los datos del embalse
Call RellenaEmbalse(IndEmbalse, Embalse)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(93, 3)) = False Then
If Cells(93, 3).Value < Cells(93, 1).Value Then
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir un volumen útil mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(93, 3).Activate
Exit Sub
Else
If Cells(93, 3).Value > Cells(93, 2).Value Then
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir un volumen útil menor que el valor máximo",
vbExclamation, "CARHI"
Cells(93, 3).Activate
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Exit Sub
Else
Abscisa = Cells(93, 3).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos embalse").Activate
MsgBox "Ha de introducir el volumen útil", vbExclamation, "CARHI"
Cells(93, 3).Activate
Exit Sub
End If
Call ResultadoFcVolUtCota(Embalse, Abscisa, Tramo, LimAplic, Ordenada)
Cells(93, 4).Value = Ordenada
Cells(94, 4).Value = "Nota: el cálculo se ha realizado para el tramo " & Tramo & "
porque su límite de aplicación inmediatamente superior es " & LimAplic & " hm3 de
volumen útil"
ActiveWorkbook.Sheets("Datos embalse").Activate
Cells(93, 4).Activate
End Sub
D.6
Subrutinas correspondientes a las funciones de la central
Private Sub CotAfterb_Click()
Dim NombreCentral As String
Dim CorteCurva1 As Variant
Dim CorteCurva2 As Variant
Dim HorqMin1 As Variant
Dim HorqMax1 As Variant
Dim HorqMin2 As Variant
Dim HorqMax2 As Variant
Dim Peso1 As Variant
Dim Peso2 As Variant
Dim NCurvas As Integer
Dim LimAplicInf As Variant
Dim LimAplicSup As Variant
Dim Abscisa As Variant
Dim OrdenadaA As Variant
Dim OrdenadaB As Variant
Dim OrdenadaC As Variant
Dim OrdenadaD As Variant
Dim Ordenada As Variant
Dim Funcion As String
Dim a0 As Variant
Dim a1 As Variant
Dim a2 As Variant
Dim a3 As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(167, 4)) = False Then
If Cells(167, 4).Value < Cells(167, 2).Value Then
145
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
146
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal total mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(167, 4).Activate
Exit Sub
Else
If Cells(167, 4).Value > Cells(167, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal total menor que el valor máximo",
vbExclamation, "CARHI"
Cells(167, 4).Activate
Exit Sub
Else
Abscisa = Cells(167, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal total", vbExclamation, "CARHI"
Cells(167, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(168, 4)) = False Then
If Cells(168, 4).Value < Cells(168, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas abajo mayor que el valor
mínimo", vbExclamation, "CARHI"
Cells(168, 4).Activate
Exit Sub
Else
If Cells(168, 4).Value > Cells(168, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas abajo menor que el
valor máximo", vbExclamation, "CARHI"
Cells(168, 4).Activate
Exit Sub
Else
CorteCurva1 = Cells(168, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir la cota de embalse aguas abajo", vbExclamation, "CARHI"
Cells(168, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(169, 4)) = False Then
If Cells(169, 4).Value < Cells(169, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por central paralela mayor que
el valor mínimo", vbExclamation, "CARHI"
Cells(169, 4).Activate
Exit Sub
Else
If Cells(169, 4).Value > Cells(169, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por central paralela menor
que el valor máximo", vbExclamation, "CARHI"
Cells(169, 4).Activate
Exit Sub
Else
CorteCurva2 = Cells(169, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal turbinado por central paralela",
vbExclamation, "CARHI"
Cells(169, 4).Activate
Exit Sub
End If
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
147
Funcion = "F3"
'Busco la función
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Sólo se cumplirá este If si tengo una curva (pues Central.Fc.Curva(NCurvas + 1) =
Central.Fc.Curva(NCurvas) = 1
If Central.Fc.Curva(NCurvas + 1) = Central.Fc.Curva(NCurvas) Then
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
a0
a1
a2
a3
=
=
=
=
Central.Fc.c0(NCurvas)
Central.Fc.c1(NCurvas)
Central.Fc.c2(NCurvas)
Central.Fc.c3(NCurvas)
Ordenada = a0 + a1 * Abscisa + a2 * Abscisa ^ 2 + a3 * Abscisa ^ 3
Else
If Cells(168, 2).Value = Cells(168, 3).Value Then 'Aunque tengo varias curvas,
no es necesaria la interpolación doble porque sólo hay un CorteCurva1
Call BuscaHorquillaCorte2(Central, Funcion, HorqMin, HorqMax, CorteCurva2)
Call ResultadoFcPolinomDoble(Central, Abscisa, CorteCurva1, HorqMin,
Funcion, OrdenadaMin)
Call ResultadoFcPolinomDoble(Central, Abscisa, CorteCurva1, HorqMax,
Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva2, OrdenadaMin, OrdenadaMax,
Ordenada)
Else
If Cells(169, 2).Value = Cells(169, 3).Value Then 'Aunque tengo varias
curvas, no es necesaria la interpolación doble porque sólo hay un CorteCurva2
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva1,
LimAplicInf, LimAplicSup)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMin, CorteCurva2,
Funcion, OrdenadaMin)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMax, CorteCurva2,
Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva1, OrdenadaMin, OrdenadaMax,
Ordenada)
Else
'Interpolación doble
Call BuscaHorquillaDoble(Central, Funcion, CorteCurva1, CorteCurva2,
HorqMin1, HorqMax1, HorqMin2, HorqMax2)
Peso1 = (CorteCurva1 - HorqMin1) / (HorqMax1 - HorqMin1)
Peso2 = (CorteCurva2 - HorqMin2) / (HorqMax2 - HorqMin2)
Call
Funcion, OrdenadaA)
Call
Funcion, OrdenadaB)
Call
Funcion, OrdenadaC)
Call
Funcion, OrdenadaD)
ResultadoFcPolinomDoble(Central, Abscisa, HorqMin1, HorqMin2,
ResultadoFcPolinomDoble(Central, Abscisa, HorqMin1, HorqMax2,
ResultadoFcPolinomDoble(Central, Abscisa, HorqMax1, HorqMax2,
ResultadoFcPolinomDoble(Central, Abscisa, HorqMax1, HorqMin2,
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
148
Ordenada = (1 - Peso1) * (1 - Peso2) * OrdenadaA + (1 - Peso1) * Peso2 *
OrdenadaB + Peso1 * Peso2 * OrdenadaC + Peso1 * (1 - Peso2) * OrdenadaD
End If
End If
End If
Cells(167, 5).Value = Ordenada
ActiveWorkbook.Sheets("Datos central").Activate
Cells(167, 5).Activate
End Sub
Private Sub PerdCarga_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim Funcion As String
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(175, 4)) = False Then
If Cells(175, 4).Value < Cells(175, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por grupo mayor que el valor
mínimo", vbExclamation, "CARHI"
Cells(175, 4).Activate
Exit Sub
Else
If Cells(175, 4).Value > Cells(175, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por grupo menor que el valor
máximo", vbExclamation, "CARHI"
Cells(175, 4).Activate
Exit Sub
Else
Abscisa = Cells(175, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal turbinado por grupo", vbExclamation, "CARHI"
Cells(175, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(176, 4)) = False Then
If Cells(176, 4).Value < Cells(176, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos mayor que el valor mínimo",
vbExclamation, "CARHI"
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
149
Cells(176, 4).Activate
Exit Sub
Else
If Cells(176, 4).Value > Cells(176, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos menor que el valor máximo",
vbExclamation, "CARHI"
Cells(176, 4).Activate
Exit Sub
Else
CorteCurva = Cells(176, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el número de grupos", vbExclamation, "CARHI"
Cells(176, 4).Activate
Exit Sub
End If
Funcion = "F4"
Call ResultadoFcPolinom(Central, Abscisa, CorteCurva, Funcion, Ordenada)
Cells(175, 5).Value = Ordenada
ActiveWorkbook.Sheets("Datos central").Activate
Cells(175, 5).Activate
End Sub
Private Sub Pgen_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim HorqMin As Variant
Dim HorqMax As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim OrdenadaMin As Variant
Dim OrdenadaMax As Variant
Dim Funcion As String
Dim LimAplicInf As Variant
Dim LimAplicSup As Variant
Dim LimAplicReal As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Borro los posibles derivados de un posible cálculo anterior
ActiveWorkbook.Sheets("Datos central").Activate
Range("E195").Select
Selection.ClearContents
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(194, 4)) = False Then
If Cells(194, 4).Value < Cells(194, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal mayor que el valor mínimo",
vbExclamation, "CARHI"
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
150
Cells(194, 4).Activate
Exit Sub
Else
If Cells(194, 4).Value > Cells(194, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal menor que el valor máximo",
vbExclamation, "CARHI"
Cells(194, 4).Activate
Exit Sub
Else
Abscisa = Cells(194, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal", vbExclamation, "CARHI"
Cells(194, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(195, 4)) = False Then
If Cells(195, 4).Value < Cells(195, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(195, 4).Activate
Exit Sub
Else
If Cells(195, 4).Value > Cells(195, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(195, 4).Activate
Exit Sub
Else
CorteCurva = Cells(195, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto neto", vbExclamation, "CARHI"
Cells(195, 4).Activate
Exit Sub
End If
Funcion = "F7"
'Interpolación simple
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, Abscisa, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Abscisa, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
Call Interpola(HorqMin, HorqMax, CorteCurva, LimAplicInf, LimAplicSup, LimAplicReal)
'Compruebo si el usuario ha introducido una Abscisa mayor que el LimAplicReal
(interpolado)
If Abscisa < LimAplicReal Then
Cells(194, 5).Value = Ordenada
Else
'Advierto al usuario que el límite de aplicación real (interpolado) es inferior
a la abscisa que ha introducido, por lo que es el valor que se ha usado al hacer el
cálculo
Cells(195, 5).Value = "Nota: el cálculo se ha realizado para un caudal máximo de
" & LimAplicReal & " m^3/s, menor que el valor de " & Abscisa & " m^3/s introducido en
un principio"
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Cells(194, 4).Value = LimAplicReal
Cells(194, 5).Value = Ordenada
End If
ActiveWorkbook.Sheets("Datos central").Activate
Cells(194, 5).Activate
End Sub
Private Sub PMax_Click()
Dim
Dim
Dim
Dim
Dim
NombreCentral As String
CorteCurva As Variant
Abscisa As Variant
Ordenada As Variant
Funcion As String
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(182, 4)) = False Then
If Cells(182, 4).Value < Cells(182, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(182, 4).Activate
Exit Sub
Else
If Cells(182, 4).Value > Cells(182, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(182, 4).Activate
Exit Sub
Else
Abscisa = Cells(182, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto neto", vbExclamation, "CARHI"
Cells(182, 4).Activate
Exit Sub
End If
CorteCurva = 0
Funcion = "F5"
Call ResultadoFcPolinom(Central, Abscisa, CorteCurva, Funcion, Ordenada)
Cells(182, 5).Value = Ordenada
ActiveWorkbook.Sheets("Datos central").Activate
151
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
152
Cells(182, 5).Activate
End Sub
Private Sub PMaxBomb_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim Curva As Integer
Dim LimAplic As Variant
Dim Funcion As String
Const NMaxCurvas = 100 'mayor que la suma del número de de todas las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(211, 4)) = False Then
If Cells(211, 4).Value < Cells(211, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto bruto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(211, 4).Activate
Exit Sub
Else
If Cells(211, 4).Value > Cells(211, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto bruto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(211, 4).Activate
Exit Sub
Else
Abscisa = Cells(211, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto bruto", vbExclamation, "CARHI"
Cells(211, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(212, 4)) = False Then
If Cells(212, 4).Value < Cells(212, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(212, 4).Activate
Exit Sub
Else
If Cells(212, 4).Value > Cells(212, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos menor que el valor máximo",
vbExclamation, "CARHI"
Cells(212, 4).Activate
Exit Sub
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
153
Else
CorteCurva = Cells(212, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el número de grupos", vbExclamation, "CARHI"
Cells(212, 4).Activate
Exit Sub
End If
Funcion = "F9"
Call ResultadoFcPolinomBomb(Central, Abscisa, CorteCurva, Funcion, Ordenada, Curva,
LimAplic)
Cells(211, 5).Value = Ordenada
Cells(212, 5).Value = "Nota: el cálculo se ha realizado para la curva " & Curva & "
porque su límite de aplicación es " & LimAplic & " m de salto bruto máximo"
ActiveWorkbook.Sheets("Datos central").Activate
Cells(211, 5).Activate
End Sub
Private Sub QGen_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim HorqMin As Variant
Dim HorqMax As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim OrdenadaMin As Variant
Dim OrdenadaMax As Variant
Dim Funcion As String
Dim LimAplicInf As Variant
Dim LimAplicSup As Variant
Dim LimAplicReal As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Borro los posibles derivados de un posible cálculo anterior
ActiveWorkbook.Sheets("Datos central").Activate
Range("E202").Select
Selection.ClearContents
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(201, 4)) = False Then
If Cells(201, 4).Value < Cells(201, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una potencia mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(201, 4).Activate
Exit Sub
Else
If Cells(201, 4).Value > Cells(201, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una potencia menor que el valor máximo",
vbExclamation, "CARHI"
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
154
Cells(201, 4).Activate
Exit Sub
Else
Abscisa = Cells(201, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir la potencia", vbExclamation, "CARHI"
Cells(201, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(202, 4)) = False Then
If Cells(202, 4).Value < Cells(202, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(201, 4).Activate
Exit Sub
Else
If Cells(202, 4).Value > Cells(202, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(201, 4).Activate
Exit Sub
Else
CorteCurva = Cells(202, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto neto", vbExclamation, "CARHI"
Cells(201, 4).Activate
Exit Sub
End If
Funcion = "F8"
'Interpolación simple
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, Abscisa, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Abscisa, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
Call Interpola(HorqMin, HorqMax, CorteCurva, LimAplicInf, LimAplicSup, LimAplicReal)
'Compruebo si el usuario ha introducido una Abscisa mayor que el LimAplicReal
(interpolado)
If Abscisa < LimAplicReal Then
Cells(201, 5).Value = Ordenada
Else
'Advierto al usuario que el límite de aplicación real (interpolado) es inferior
a la abscisa que ha introducido, por lo que es el valor que se ha usado al hacer el
cálculo
Cells(202, 5).Value = "Nota: el cálculo se ha realizado para una potencia máxima
de " & LimAplicReal & " MW, menor que el valor de " & Abscisa & " MW introducido en un
principio"
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
Cells(201, 4).Value = LimAplicReal
Cells(201, 5).Value = Ordenada
End If
ActiveWorkbook.Sheets("Datos central").Activate
Cells(201, 5).Activate
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
End Sub
Private Sub QMax_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim Funcion As String
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(188, 4)) = False Then
If Cells(188, 4).Value < Cells(188, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(188, 4).Activate
Exit Sub
Else
If Cells(188, 4).Value > Cells(188, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(188, 4).Activate
Exit Sub
Else
Abscisa = Cells(188, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto neto", vbExclamation, "CARHI"
Cells(188, 4).Activate
Exit Sub
End If
CorteCurva = 0
Funcion = "F6"
Call ResultadoFcPolinom(Central, Abscisa, CorteCurva, Funcion, Ordenada)
Cells(188, 5).Value = Ordenada
ActiveWorkbook.Sheets("Datos central").Activate
Cells(188, 5).Activate
End Sub
Private Sub QMaxBomb_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim Curva As Integer
Dim LimAplic As Variant
Dim Funcion As String
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
155
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
156
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(218, 4)) = False Then
If Cells(218, 4).Value < Cells(218, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto bruto mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(218, 4).Activate
Exit Sub
Else
If Cells(218, 4).Value > Cells(218, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto bruto menor que el valor máximo",
vbExclamation, "CARHI"
Cells(218, 4).Activate
Exit Sub
Else
Abscisa = Cells(218, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto bruto", vbExclamation, "CARHI"
Cells(218, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(219, 4)) = False Then
If Cells(219, 4).Value < Cells(219, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(219, 4).Activate
Exit Sub
Else
If Cells(219, 4).Value > Cells(219, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos menor que el valor máximo",
vbExclamation, "CARHI"
Cells(219, 4).Activate
Exit Sub
Else
CorteCurva = Cells(219, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el número de grupos", vbExclamation, "CARHI"
Cells(219, 4).Activate
Exit Sub
End If
Funcion = "F10"
Call ResultadoFcPolinomBomb(Central, Abscisa, CorteCurva, Funcion, Ordenada, Curva,
LimAplic)
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
157
Cells(218, 5).Value = Ordenada
Cells(219, 5).Value = "Nota: el cálculo se ha realizado para la curva " & Curva & "
porque su límite de aplicación es " & LimAplic & " m de salto bruto máximo"
ActiveWorkbook.Sheets("Datos central").Activate
Cells(218, 5).Activate
End Sub
Private Sub Rto_Click()
Dim NombreCentral As String
Dim CorteCurva As Variant
Dim HorqMin As Variant
Dim HorqMax As Variant
Dim Abscisa As Variant
Dim Ordenada As Variant
Dim OrdenadaMin As Variant
Dim OrdenadaMax As Variant
Dim Funcion As String
Dim g As Variant
Dim Densidad As Variant
Dim RtoAlternador As Variant
Dim LimAplicInf As Variant
Dim LimAplicSup As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
'Cargo los datos que ha introducido el usuario
If IsEmpty(Cells(228, 4)) = False Then
If Cells(228, 4).Value < Cells(228, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(228, 4).Activate
Exit Sub
Else
If Cells(228, 4).Value > Cells(228, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal menor que el valor máximo",
vbExclamation, "CARHI"
Cells(228, 4).Activate
Exit Sub
Else
Abscisa = Cells(228, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal", vbExclamation, "CARHI"
Cells(228, 4).Activate
Exit Sub
End If
If IsEmpty(Cells(229, 4)) = False Then
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
158
If Cells(229, 4).Value < Cells(229, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto mayor que el valor mínimo",
vbExclamation, "CARHI"
Exit Sub
Else
If Cells(229, 4).Value > Cells(229, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un salto neto menor que el valor máximo",
vbExclamation, "CARHI"
Exit Sub
Else
CorteCurva = Cells(229, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el salto neto", vbExclamation, "CARHI"
Exit Sub
End If
Funcion = "F7"
'Interpolación simple
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, Abscisa, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Abscisa, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
'Rendimiento total (paso los MW a W multiplicando por 1000000)
g = 9.8 'Considero g= 9,8 m/s^2
Densidad = 1000 'Considero la densidad del agua igual a 1000 kg/m^3
Ordenada = Ordenada * 1000000 / (g * Densidad * CorteCurva * Abscisa)
'Rendimiento de la turbina es rendimiento total entre rendimiento del alternador
RtoAlternador = 0.98 'Considero 0,98 un rendimiento típico de alternador
Ordenada = Ordenada / RtoAlternador
Cells(228, 5).Value = Ordenada
ActiveWorkbook.Sheets("Datos central").Activate
Cells(228, 5).Activate
End Sub
D.7
Subrutinas de cálculo polinómico del embalse
Sub ResultadoFcVolUtCota(ByRef Embalse As Emb, ByVal Abscisa As Variant, ByRef Tramo As
Integer, ByRef LimAplic As Variant, ByRef Ordenada As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta el
código
Application.ScreenUpdating = False
Const NMaxTramos = 14
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
i As Integer
a0 As Variant
a1 As Variant
a2 As Variant
a3 As Variant
Cont As Integer
RefQueMeLlevoUnDiaEncontrar As Variant
UltTramo As Integer
If Embalse.Fc.VMin(2) = Embalse.Fc.VMin(3) Then 'Hay dos tramos de F2
Cont = 4
Else 'Hay un tramo de F2
Cont = 3
End If
UltTramo = 0
For i = 1 To NMaxTramos
If Embalse.Fc.Curva(Cont) = Embalse.Fc.RgVTot(Cont) Then 'Sólo hay un tramo
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Exit For
Else
'VRef es el valor de abscisa del knot
If Embalse.Fc.VRef(Cont + 1) < Abscisa Then 'No estoy en el tramo
'RgVTot es el número máximo de curvas
If Embalse.Fc.Curva(Cont) = Embalse.Fc.RgVTot(Cont) - 1 Then 'Ya sólo
queda un tramo, así que salgo del bucle for
Cont = Cont + 1 'Me posiciono en el último tramo que queda
UltTramo = 1
i = i + 1
Exit For 'Salgo del bucle
End If
Cont = Cont + 1
Else 'Ya estoy en el tramo
Exit For
End If
End If
Next i
a0 = Embalse.Fc.c0(Cont)
a1 = Embalse.Fc.c1(Cont)
a2 = Embalse.Fc.c2(Cont)
a3 = Embalse.Fc.c3(Cont)
RefQueMeLlevoUnDiaEncontrar = Embalse.Fc.VRef(Cont)
Ordenada = a0 + a1 * (Abscisa - RefQueMeLlevoUnDiaEncontrar) + a2 * (Abscisa RefQueMeLlevoUnDiaEncontrar) ^ 2 + a3 * (Abscisa - RefQueMeLlevoUnDiaEncontrar) ^ 3
Tramo = i
If UltTramo = 1 Then 'Estoy en el último tramo
LimAplic = Embalse.Fc.VMax(Cont)
Else
LimAplic = Embalse.Fc.VRef(Cont + 1)
End If
Application.ScreenUpdating = True
End Sub
Sub ResultadoFcCotaVTot(ByRef Embalse As Emb, ByVal Abscisa As Variant, ByRef Ordenada
As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Dim
Dim
Dim
Dim
Dim
Dim
Dim
a0 As Variant
a1 As Variant
a2 As Variant
a3 As Variant
a4 As Variant
CotRef As Double
Cont As Integer
If Embalse.Fc.VMin(2) = Embalse.Fc.VMin(3) Then 'Hay dos tramos de F2
If Abscisa < Embalse.Fc.RgVTot(2) Then
Cont = 2
Else
Cont = 3
End If
Else 'Hay un tramo de F2
Cont = 2
End If
a0
a1
a2
a3
=
=
=
=
Embalse.Fc.c0(Cont)
Embalse.Fc.c1(Cont)
Embalse.Fc.c2(Cont)
Embalse.Fc.c3(Cont)
159
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
160
a4 = Embalse.Fc.c4(Cont)
CotRef = Embalse.Fc.VRef(Cont)
Ordenada = a0 + a1 * (Abscisa - CotRef) + a2 * (Abscisa - CotRef) ^ 2 + a3 *
(Abscisa - CotRef) ^ 3 + a4 * (Abscisa - CotRef) ^ 4
Application.ScreenUpdating = True
End Sub
Sub ResultadoFcCotaVUt(ByRef Embalse As Emb, ByVal Abscisa As Variant, ByRef Ordenada As
Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Dim
Dim
Dim
Dim
Dim
Dim
a0 As Variant
a1 As Variant
a2 As Variant
a3 As Variant
a4 As Variant
CotRef As Double
a0 = Embalse.Fc.c0(1)
a1 = Embalse.Fc.c1(1)
a2 = Embalse.Fc.c2(1)
a3 = Embalse.Fc.c3(1)
a4 = Embalse.Fc.c4(1)
CotRef = Embalse.Fc.VRef(1)
Ordenada = a0 + a1 * (Abscisa - CotRef) + a2 * (Abscisa - CotRef) ^ 2 + a3 *
(Abscisa - CotRef) ^ 3 + a4 * (Abscisa - CotRef) ^ 4
Application.ScreenUpdating = True
End Sub
D.8
Subrutinas de cálculo polinómico y de interpolación simple y doble de la
central
Sub BuscaHorquilla(ByRef Central As Ctr, ByVal Funcion As String, ByRef HorqMin As
Variant, ByRef HorqMax As Variant, ByVal CorteCurva As Variant, ByRef LimAplicInf As
Variant, ByRef LimAplicSup As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim NCurvas As Integer
Dim Cont As Integer
Dim MiniCont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Busco la horquilla dentro de la función concreta
For Cont = NCurvas To NMaxCurvas
If Central.Fc.Cor1(Cont) >= CorteCurva Then
If Cont = NCurvas Then 'Sólo entro aquí si CorteCurva justo es la frontera
inferior
HorqMin = Central.Fc.Cor1(Cont)
LimAplicInf = Central.Fc.VMax(Cont)
MiniCont = Cont
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
161
While Central.Fc.Cor1(MiniCont) = HorqMin
MiniCont = MiniCont + 1
Wend
HorqMax = Central.Fc.Cor1(MiniCont)
LimAplicSup = Central.Fc.VMax(MiniCont)
Exit For
Else
HorqMin = Central.Fc.Cor1(Cont - 1)
LimAplicInf = Central.Fc.VMax(Cont - 1)
HorqMax = Central.Fc.Cor1(Cont)
LimAplicSup = Central.Fc.VMax(Cont)
Exit For
End If
End If
Next Cont
End Sub
Sub BuscaHorquillaCorte2(ByRef Central As Ctr, ByVal Funcion As String, ByRef HorqMin As
Variant, ByRef HorqMax As Variant, ByVal CorteCurva As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim NCurvas As Integer
Dim Cont As Integer
Dim MiniCont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Busco la horquilla dentro de la función concreta
For Cont = NCurvas To NMaxCurvas
If Central.Fc.Cor2(Cont) >= CorteCurva Then
If Cont = NCurvas Then 'Sólo entro aquí si CorteCurva justo es la frontera
inferior
HorqMin = Central.Fc.Cor2(Cont)
MiniCont = Cont
While Central.Fc.Cor2(MiniCont) = HorqMin
MiniCont = MiniCont + 1
Wend
HorqMax = Central.Fc.Cor2(MiniCont)
Exit For
Else
HorqMin = Central.Fc.Cor2(Cont - 1)
HorqMax = Central.Fc.Cor2(Cont)
Exit For
End If
End If
Next Cont
End Sub
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
162
Sub BuscaHorquillaDoble(ByRef Central As Ctr, ByVal Funcion As String, ByVal CorteCurva1
As Variant, ByVal CorteCurva2 As Variant, ByRef HorqMin1 As Variant, ByRef HorqMax1 As
Variant, ByRef HorqMin2 As Variant, ByRef HorqMax2 As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim
Dim
Dim
Dim
NCurvas As Integer
Cont1 As Integer
Cont2 As Integer
MiniCont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Busco la horquilla dentro de la función concreta
For Cont1 = NCurvas To NMaxCurvas
If Central.Fc.Cor1(Cont1) >= CorteCurva1 Then
If Cont1 = NCurvas Then 'Sólo entro aquí si CorteCurva1 justo es la frontera
inferior
HorqMin1 = Central.Fc.Cor1(Cont1)
MiniCont = Cont1
While Central.Fc.Cor1(MiniCont) = HorqMin1
MiniCont = MiniCont + 1
Wend
HorqMax1 = Central.Fc.Cor1(MiniCont)
Exit For
Else
HorqMin1 = Central.Fc.Cor1(Cont1 - 1)
HorqMax1 = Central.Fc.Cor1(Cont1)
Exit For
End If
End If
Next Cont1
For Cont2 = NCurvas To NMaxCurvas
If Central.Fc.Cor2(Cont2) >= CorteCurva2 Then
If Cont2 = NCurvas Then 'Sólo entro aquí si CorteCurva2 justo es la frontera
inferior
HorqMin2 = Central.Fc.Cor2(Cont2)
MiniCont = Cont2
While Central.Fc.Cor2(MiniCont) = HorqMin2
MiniCont = MiniCont + 1
Wend
HorqMax2 = Central.Fc.Cor2(MiniCont)
Exit For
Else
HorqMin2 = Central.Fc.Cor2(Cont2 - 1)
HorqMax2 = Central.Fc.Cor2(Cont2)
Exit For
End If
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
163
End If
Next Cont2
End Sub
Sub Interpola(ByVal HorqMin As Variant, ByVal HorqMax As Variant, ByVal CorteCurva As
Variant, ByVal OrdenadaMin As Variant, ByVal OrdenadaMax As Variant, ByRef Ordenada As
Variant)
Dim a As Variant
Dim b As Variant
a = (OrdenadaMax - OrdenadaMin) / (HorqMax - HorqMin)
b = OrdenadaMax - a * HorqMax
Ordenada = a * CorteCurva + b
End Sub
Sub ResultadoFcPolinom(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal CorteCurva
As Variant, ByVal Funcion As String, ByRef Ordenada As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim
Dim
Dim
Dim
Dim
Dim
a0 As Variant
a1 As Variant
a2 As Variant
a3 As Variant
NCurvas As Integer
Cont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Busco la curva dentro de la función concreta
For Cont = NCurvas To NMaxCurvas
If Central.Fc.Cor1(Cont) = CorteCurva Then
Exit For
End If
Next Cont
a0
a1
a2
a3
=
=
=
=
Central.Fc.c0(Cont)
Central.Fc.c1(Cont)
Central.Fc.c2(Cont)
Central.Fc.c3(Cont)
Ordenada = a0 + a1 * Abscisa + a2 * Abscisa ^ 2 + a3 * Abscisa ^ 3
Application.ScreenUpdating = True
End Sub
Sub ResultadoFcPolinomBomb(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal
CorteCurva As Variant, ByVal Funcion As String, ByRef Ordenada As Variant, ByRef Curva
As Integer, ByRef LimAplic As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim a0 As Variant
Dim a1 As Variant
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim
Dim
Dim
Dim
a2 As Variant
a3 As Variant
NCurvas As Integer
Cont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
Curva = 1
'Busco la curva en concreto
For Cont = NCurvas To NMaxCurvas
'Dentro del if cojo la curva (como máximo hay 3) para el NGrupos = CorteCurva
tal que el salto bruto esté dentro del límite de aplicación
If Central.Fc.Cor1(Cont) = CorteCurva Then
If Abscisa < Central.Fc.VMax(Cont) Then 'Entro en curva 1 para NGrupos =
CorteCurva
Exit For
Else
If Abscisa < Central.Fc.VMax(Cont + 1) Then 'Entro en curva 2 para
NGrupos = CorteCurva
Cont = Cont + 1
Curva = Curva + 1
Exit For
Else 'Entro en curva 3 para NGrupos = CorteCurva
Cont = Cont + 2
Curva = Curva + 2
Exit For
End If
End If
End If
Curva = Curva + 1
Next Cont
a0
a1
a2
a3
=
=
=
=
Central.Fc.c0(Cont)
Central.Fc.c1(Cont)
Central.Fc.c2(Cont)
Central.Fc.c3(Cont)
Ordenada = a0 + a1 * Abscisa + a2 * Abscisa ^ 2 + a3 * Abscisa ^ 3
LimAplic = Central.Fc.VMax(Cont)
Application.ScreenUpdating = True
End Sub
Sub ResultadoFcPolinomDoble(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal
CorteCurva1 As Variant, ByVal CorteCurva2 As Variant, ByVal Funcion As String, ByRef
Ordenada As Variant)
'Para que el usuario no vea cómo se pasa de una hoja a otra
Application.ScreenUpdating = False
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Dim a0 As Variant
Dim a1 As Variant
Dim a2 As Variant
Dim a3 As Variant
Dim NCurvas As Integer
Dim Cont As Integer
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
164
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
End If
Next NCurvas
'Busco la curva dentro de la función concreta
For Cont = NCurvas To NMaxCurvas
If Central.Fc.Cor1(Cont) = CorteCurva1 Then
If Central.Fc.Cor2(Cont) = CorteCurva2 Then
Exit For
End If
End If
Next Cont
a0
a1
a2
a3
=
=
=
=
Central.Fc.c0(Cont)
Central.Fc.c1(Cont)
Central.Fc.c2(Cont)
Central.Fc.c3(Cont)
Ordenada = a0 + a1 * Abscisa + a2 * Abscisa ^ 2 + a3 * Abscisa ^ 3
Application.ScreenUpdating = True
End Sub
D.9
Proceso iterativo para unas condiciones de funcionamiento de una central
Sub Iteracion()
'Para que el usuario no vea cómo se pasa de una hoja a otra mientras se ejecuta
el código
Application.ScreenUpdating = False
'Variables que introduce el usuario (inputs)
Dim Potencia As Variant
Dim QVert As Variant
Dim Caar As Variant
Dim Caab As Variant
Dim CaabMax As Variant
Dim CaabMin As Variant
Dim Qcp As Variant
Dim QcpMax As Variant
Dim QcpMin As Variant
Dim NGr As Variant
'Variables para realizar la iteración
Dim QInic As Variant
Dim QNuevo As Variant
Dim QAntig As Variant
Dim QMax As Variant
Dim Ajuste As Variant
Dim HnMin As Variant
Dim HnMax As Variant
Dim NVueltas As Variant
Dim NVueltasMax As Variant
Dim PMax As Variant
Dim QMin As Variant
Dim PAntigPar As Variant
Dim PAntigImpar As Variant
Dim PesoPar As Variant
Dim PesoImpar As Variant
Dim CopiaQAntig
'Variables que se obtienen (outputs)
Dim CDes As Variant
Dim PCarga As Variant
Dim SaltoB As Variant
Dim SaltoN As Variant
Dim PAntig As Variant
Dim Par As Variant
Dim
Dim
Dim
Dim
CoefEnerg As Variant
CoefEnergMxRto As Variant
CoefEnergPlenaCarga As Variant
QMxRto As Variant
165
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim
Dim
Dim
Dim
Dim
166
PMxRto As Variant
PMx As Variant
QMx As Variant
PBomb As Variant
QBomb As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Dim NombreCentral As String
Dim IndCentral As Integer
Dim Central As Ctr
ReDim Central.Fc.Nb(1 To NMaxCurvas)
ReDim Central.Fc.Curva(1 To NMaxCurvas)
ReDim Central.Fc.c0(1 To NMaxCurvas)
ReDim Central.Fc.c1(1 To NMaxCurvas)
ReDim Central.Fc.c2(1 To NMaxCurvas)
ReDim Central.Fc.c3(1 To NMaxCurvas)
ReDim Central.Fc.Cor1(1 To NMaxCurvas)
ReDim Central.Fc.Cor2(1 To NMaxCurvas)
ReDim Central.Fc.VMin(1 To NMaxCurvas)
ReDim Central.Fc.VMax(1 To NMaxCurvas)
'Compruebo que todos los valores introducidos están dentro de rango
'Potencia
PMax = Cells(239, 3).Value
If IsEmpty(Cells(239, 4)) = False Then
If Cells(239, 4).Value < Cells(239, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una potencia mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(239, 4).Activate
Exit Sub
Else
If Cells(239, 4).Value > Cells(239, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una potencia menor que el valor máximo",
vbExclamation, "CARHI"
Cells(239, 4).Activate
Exit Sub
Else
Potencia = Cells(239, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir la potencia", vbExclamation, "CARHI"
Cells(239, 4).Activate
Exit Sub
End If
'Caudal vertido
If IsEmpty(Cells(240, 4)) = False Then
If Cells(240, 4).Value < Cells(240, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal vertido por la central mayor que el
valor mínimo", vbExclamation, "CARHI"
Cells(240, 4).Activate
Exit Sub
Else
If Cells(240, 4).Value > Cells(240, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal vertido por la central menor que el
valor máximo", vbExclamation, "CARHI"
Cells(240, 4).Activate
Exit Sub
Else
QVert = Cells(240, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
167
MsgBox "Ha de introducir el caudal vertido por la central", vbExclamation,
"CARHI"
Cells(240, 4).Activate
Exit Sub
End If
'cota de embalse aguas arriba
If IsEmpty(Cells(241, 4)) = False Then
If Cells(241, 4).Value < Cells(241, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas arriba mayor que el
valor mínimo", vbExclamation, "CARHI"
Cells(241, 4).Activate
Exit Sub
Else
If Cells(241, 4).Value > Cells(241, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas arriba menor que el
valor máximo", vbExclamation, "CARHI"
Cells(241, 4).Activate
Exit Sub
Else
Caar = Cells(241, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir la cota de embalse aguas arriba", vbExclamation,
"CARHI"
Cells(241, 4).Activate
Exit Sub
End If
'cota de embalse aguas abajo
CaabMin = Cells(242, 2).Value
CaabMax = Cells(242, 3).Value
If IsEmpty(Cells(242, 4)) = False Then
If Cells(242, 4).Value < CaabMin Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas abajo mayor que el
valor mínimo", vbExclamation, "CARHI"
Cells(242, 4).Activate
Exit Sub
Else
If Cells(242, 4).Value > CaabMax Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir una cota de embalse aguas abajo menor que el
valor máximo", vbExclamation, "CARHI"
Cells(242, 4).Activate
Exit Sub
Else
Caab = Cells(242, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir la cota de embalse aguas abajo", vbExclamation,
"CARHI"
Cells(242, 4).Activate
Exit Sub
End If
'caudal turbinado por central paralela
QcpMin = Cells(243, 2).Value
QcpMax = Cells(243, 3).Value
If IsEmpty(Cells(243, 4)) = False Then
If Cells(243, 4).Value < QcpMin Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por central paralela mayor
que el valor mínimo", vbExclamation, "CARHI"
Cells(243, 4).Activate
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
168
Exit Sub
Else
If Cells(243, 4).Value > QcpMax Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un caudal turbinado por central paralela
menor que el valor máximo", vbExclamation, "CARHI"
Cells(243, 4).Activate
Exit Sub
Else
Qcp = Cells(243, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el caudal turbinado por central paralela",
vbExclamation, "CARHI"
Cells(243, 4).Activate
Exit Sub
End If
'número de grupos
If IsEmpty(Cells(244, 4)) = False Then
If Cells(244, 4).Value < Cells(244, 2).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos mayor que el valor mínimo",
vbExclamation, "CARHI"
Cells(244, 4).Activate
Exit Sub
Else
If Cells(244, 4).Value > Cells(244, 3).Value Then
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir un número de grupos menor que el valor
máximo", vbExclamation, "CARHI"
Cells(244, 4).Activate
Exit Sub
Else
NGr = Cells(244, 4).Value
End If
End If
Else
ActiveWorkbook.Sheets("Datos central").Activate
MsgBox "Ha de introducir el número de grupos", vbExclamation, "CARHI"
Cells(244, 4).Activate
Exit Sub
End If
'Creo la estructura
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
'Relleno en estructura "Central" con todos los datos de la central
Call RellenaCentral(IndCentral, Central)
ActiveWorkbook.Sheets("Datos central").Activate
HnMin = Cells(182, 2).Value
HnMax = Cells(182, 3).Value
'Obtengo un caudal inicial como punto de partida de la iteración
Call ItQInic(Central, Potencia, HnMin, HnMax, QInic)
QMin =
QMax =
PAntig
QNuevo
Ajuste
Cells(194, 2).Value
Cells(194, 3).Value
= 0
= QInic
= 100
NVueltas = 0
Par = 1
SeSaleRango = 0
NVueltasMax = 100
'Iteración
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
While (Potencia > (PAntig + (PMax / Ajuste)) Or Potencia < (PAntig - (PMax /
Ajuste)) And NVueltas < NVueltasMax)
Call ItCDes(Central, QNuevo, QVert, NGr, Caab, Qcp, CDes, CaabMin, CaabMax,
QcpMin, QcpMax)
SaltoB = Caar - CDes
Call ItPCarga(Central, QNuevo, NGr, PCarga)
SaltoN = SaltoB - PCarga
Call ItPGen(Central, QNuevo, SaltoN, PAntig)
CopiaQAntig = QAntig
QAntig = QNuevo
If PAntig < Potencia Then
QNuevo = QAntig + (QMax / Ajuste)
Else
QNuevo = QAntig - (QMax / Ajuste)
End If
NVueltas = NVueltas + 1
If PAntig = PAntigPar Then 'Está "vibrando" alrededor de dos valores que
horquillan a PAntig +/- Error
NVueltas = NVueltasMax + 100
'Pesos de desvio respecto de Potencia
PesoPar = Potencia - PAntigPar
If PesoPar < 0 Then
PesoPar = PesoPar * (-1)
End
PesoImpar = Potencia - PAntigImpar
If PesoImpar < 0 Then
PesoImpar = PesoImpar * (-1)
End
PesoPar = PesoImpar / (PesoPar + PesoImpar)
PesoImpar = PesoPar / (PesoPar + PesoImpar)
'Salgo de la iteración con valor de caudal intermedio, según pesos
QAntig = QAntig * PesoPar + CopiaQAntig * PesoImpar
End If
If (NVueltas > NVueltasMax) And (NVueltas < NVueltasMax + 99) Then 'Sumo 99
porque cuando vibra sumo 100
SeSaleRango = 1
End If
Par = Par * (-1)
If Par = 1 Then 'PAntigPar guarda el valor de PAntig para NVueltas par
PAntigPar = PAntig
Else
PAntigImpar = PAntig
End If
Wend
If SeSaleRango = 0 Then
'Características que se obtienen directamente
Cells(252, 2).Value = QAntig
Cells(256, 2).Value = CDes
Cells(259, 2).Value = PCarga
Cells(257, 2).Value = SaltoB
Cells(258, 2).Value = SaltoN
'Características que requieren ciertos cálculos
CoefEnerg = Potencia * 1000 / QAntig / 3600 ' Multiplico por 1000 para paar los
MW a kW, y divido entre 3600 para tener h en vez de s
Cells(253, 2).Value = CoefEnerg
Call HallaCoefEnergPlenaCarga(Central, SaltoN, CoefEnergPlenaCarga, PMx, QMx)
169
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
170
Cells(255, 2).Value = CoefEnergPlenaCarga
Cells(262, 2).Value = PMx
Cells(263, 2).Value = QMx
Call HallaCoefEnergMxRto(Central, SaltoN, QMin, CoefEnergMxRto, PMxRto, QMxRto)
Cells(254, 2).Value = CoefEnergMxRto
Cells(260, 2).Value = QMxRto
Cells(261, 2).Value = PMxRto
'Sólo relleno estas características si la central bombea
If (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral =
11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Then
Call HallaPBomb(Central, SaltoB, NGr, PBomb)
Cells(264, 2).Value = PBomb
Call HallaQBomb(Central, SaltoB, NGr, QBomb)
Cells(265, 2).Value = QBomb
End If
Else
Cells(252, 2).Value = "Fuera de rango"
Cells(256, 2).Value = "Fuera de rango"
Cells(259, 2).Value = "Fuera de rango"
Cells(257, 2).Value = "Fuera de rango"
Cells(258, 2).Value = "Fuera de rango"
Cells(253, 2).Value = "Fuera de rango"
Cells(255, 2).Value = "Fuera de rango"
Cells(262, 2).Value = "Fuera de rango"
Cells(263, 2).Value = "Fuera de rango"
Cells(254, 2).Value = "Fuera de rango"
Cells(260, 2).Value = "Fuera de rango"
Cells(261, 2).Value = "Fuera de rango"
'Sólo relleno estas características si la central bombea
If (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral =
11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Then
Cells(264, 2).Value = "Fuera de rango"
Cells(265, 2).Value = "Fuera de rango"
End If
End If
Application.ScreenUpdating = True
End Sub
D.10 Subrutinas en las que se apoya la iteración para unas condiciones de
funcionamiento
Sub HallaCoefEnergMxRto(ByRef Central As Ctr, ByVal SaltoNeto As Variant, ByVal QMin
As Byte, ByRef CoefEnergMxRto As Variant, ByRef PMxRto As Variant, ByRef QMxRto As
Variant)
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
HorqMin As Variant
HorqMax As Variant
Caudal As Variant
Potencia As Variant
Funcion As String
Ordenada
OrdenadaMin As Variant
OrdenadaMax As Variant
CorteCurva As Variant
CorteCurvabis As Variant
LimAplicInf As Variant
LimAplicSup As Variant
Dim Ajuste As Variant
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim
Dim
Dim
Dim
171
Cont As Integer
g As Variant
Densidad As Variant
RtoAlternador As Variant
g = 9.8 'Considero g= 9,8 m/s^2
Densidad = 1000 'Considero la densidad del agua igual a 1000 kg/m^3
RtoAlternador = 0.98 'Considero 0,98 un rendimiento típico de alternador
Ajuste = 100
Caudal = QMin
CoefEnergMxRto = 0
CorteCurva = SaltoNeto
CorteCurvabis = 0
'Hallo el caudal máximo para el salto neto dado
Funcion = "F6"
Call ResultadoFcPolinom(Central, CorteCurva, CorteCurvabis, Funcion, QMax)
'Hallo HorqMin (salto neto inmediatamente inferior) y HorqMax (salto neto
inmediatamente superior). LimAplic no me importan en este cálculo
Funcion = "F7"
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
For Cont = 1 To Ajuste 'Recorro exactamente un número Ajuste de puntos (Q, P)
porque el paso es (QMax - QMin)/Ajuste
Caudal = Caudal + (QMax - QMin) / Ajuste
Call ResultadoFcPolinom(Central, Caudal, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Caudal, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax,
Ordenada)
Potencia = Ordenada
Ordenada = Potencia * 1000 / Caudal / 3600
If Ordenada > CoefEnergMxRto Then
CoefEnergMxRto = Ordenada
PMxRto = Potencia
QMxRto = Caudal
End If
Next Cont
End Sub
Sub HallaPBomb(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal CorteCurva As
Variant, ByRef Ordenada As Variant)
Dim Curva As Integer
Dim LimAplic As Variant
Dim Funcion As String
Funcion = "F9"
Call ResultadoFcPolinomBomb(Central, Abscisa, CorteCurva, Funcion, Ordenada,
Curva, LimAplic)
End Sub
Sub HallaQBomb(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal NGr As Variant,
ByRef Ordenada As Variant)
Dim Curva As Integer
Dim LimAplic As Variant
Dim Funcion As String
Funcion = "F10"
Call ResultadoFcPolinomBomb(Central, Abscisa, CorteCurva, Funcion, Ordenada,
Curva, LimAplic)
Cells(218, 5).Value = Ordenada
End Sub
Sub HallaCoefEnergPlenaCarga(ByRef Central As Ctr, ByVal SaltoN As Variant, ByRef
CoefEnergPlenaCarga As Variant, ByRef PMax As Variant, ByRef QMax As Variant)
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
172
CorteCurva As Variant
Funcion As String
LimAplicInf As Variant
LimAplicSup As Variant
OrdenadaMin As Variant
OrdenadaMax As Variant
HorqMin As Variant
HorqMax As Variant
CorteCurva = 0
Funcion = "F6"
Call ResultadoFcPolinom(Central, SaltoN, CorteCurva, Funcion, QMax)
'Hallo HorqMin (salto neto inmediatamente inferior) y HorqMax (salto neto
inmediatamente superior). LimAplic no me importan en este cálculo
Funcion = "F7"
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, SaltoN, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, QMax, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, QMax, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, SaltoN, OrdenadaMin, OrdenadaMax, PMax)
CoefEnergPlenaCarga = PMax * 1000 / QMax / 3600 ' Multiplico por 1000 para paar
los MW a kW, y divido entre 3600 para tener h en vez de s
End Sub
Sub ItPGen(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal CorteCurva As
Variant, ByRef Ordenada As Variant)
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
HorqMin As Variant
HorqMax As Variant
OrdenadaMin As Variant
OrdenadaMax As Variant
Funcion As String
LimAplicInf As Variant
LimAplicSup As Variant
LimAplicReal As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de todas las
funciones
Funcion = "F7"
'Interpolación simple
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, Abscisa, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Abscisa, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
Call Interpola(HorqMin, HorqMax, CorteCurva, LimAplicInf, LimAplicSup,
LimAplicReal)
'Compruebo si el usuario ha introducido una Abscisa mayor que el LimAplicReal
(interpolado)
If Abscisa > LimAplicReal Then
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax,
Ordenada)
End If
End Sub
Sub ItPCarga(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal CorteCurva As
Variant, ByRef Ordenada As Variant)
Dim Funcion As String
Funcion = "F4"
Call ResultadoFcPolinom(Central, Abscisa, CorteCurva, Funcion, Ordenada)
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
173
End Sub
Sub ItCDes(ByRef Central As Ctr, ByVal QAntig As Variant, ByVal QVert As Variant,
ByVal NGr As Variant, CorteCurva1 As Variant, ByVal CorteCurva2 As Variant, ByRef
Ordenada As Variant, ByVal CaabMin As Variant, ByVal CaabMax As Variant, ByVal QcpMin As
Variant, ByVal QcpMax As Variant)
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
HorqMin1 As Variant
HorqMax1 As Variant
HorqMin2 As Variant
HorqMax2 As Variant
Peso1 As Variant
Peso2 As Variant
NCurvas As Integer
LimAplicInf As Variant
LimAplicSup As Variant
Abscisa As Variant
OrdenadaA As Variant
OrdenadaB As Variant
OrdenadaC As Variant
OrdenadaD As Variant
Funcion As String
a0 As Variant
a1 As Variant
a2 As Variant
a3 As Variant
Const NMaxCurvas = 100 'mayor que la suma del número de curvas de las funciones
Abscisa = (QAntig + QVert) * NGr
Funcion = "F3"
'Busco la función
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
'Sólo se cumplirá este If si tengo una curva (pues Central.Fc.Curva(NCurvas + 1)
= Central.Fc.Curva(NCurvas) = 1
If Central.Fc.Curva(NCurvas + 1) = Central.Fc.Curva(NCurvas) Then
'Busco las características de la función en concreto
For NCurvas = 1 To NMaxCurvas
If Central.Fc.Nb(NCurvas) = Funcion Then
Exit For
End If
Next NCurvas
a0
a1
a2
a3
=
=
=
=
Central.Fc.c0(NCurvas)
Central.Fc.c1(NCurvas)
Central.Fc.c2(NCurvas)
Central.Fc.c3(NCurvas)
Ordenada = a0 + a1 * Abscisa + a2 * Abscisa ^ 2 + a3 * Abscisa ^ 3
Else
If CaabMin = CaabMax Then 'Aunque tengo varias curvas, no es necesaria la
interpolación doble porque sólo hay un CorteCurva1
Call BuscaHorquillaCorte2(Central, Funcion, HorqMin, HorqMax,
CorteCurva2)
Call ResultadoFcPolinomDoble(Central, Abscisa, CorteCurva1, HorqMin,
Funcion, OrdenadaMin)
Call ResultadoFcPolinomDoble(Central, Abscisa, CorteCurva1, HorqMax,
Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva2, OrdenadaMin, OrdenadaMax,
Ordenada)
Else
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
174
If QcpMin = QcpMax Then 'Aunque tengo varias curvas, no es necesaria la
interpolación doble porque sólo hay un CorteCurva2
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva1,
LimAplicInf, LimAplicSup)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMin, CorteCurva2,
Funcion, OrdenadaMin)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMax, CorteCurva2,
Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva1, OrdenadaMin,
OrdenadaMax, Ordenada)
Else
'Interpolación doble
Call BuscaHorquillaDoble(Central, Funcion, CorteCurva1, CorteCurva2,
HorqMin1, HorqMax1, HorqMin2, HorqMax2)
Peso1 = (CorteCurva1 - HorqMin1) / (HorqMax1 - HorqMin1)
Peso2 = (CorteCurva2 - HorqMin2) / (HorqMax2 - HorqMin2)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMin1, HorqMin2,
Funcion, OrdenadaA)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMin1, HorqMax2,
Funcion, OrdenadaB)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMax1, HorqMax2,
Funcion, OrdenadaC)
Call ResultadoFcPolinomDoble(Central, Abscisa, HorqMax1, HorqMin2,
Funcion, OrdenadaD)
Ordenada = (1 - Peso1) * (1 - Peso2) * OrdenadaA + (1 - Peso1) *
Peso2 * OrdenadaB + Peso1 * Peso2 * OrdenadaC + Peso1 * (1 - Peso2) * OrdenadaD
End If
End If
End If
End Sub
Sub ItQInic(ByRef Central As Ctr, ByVal Abscisa As Variant, ByVal HnMin As Variant,
ByVal HnMax As Variant, ByRef QInic As Variant)
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
Dim
CorteCurva As Variant
HorqMin As Variant
HorqMax As Variant
Ordenada As Variant
OrdenadaMin As Variant
OrdenadaMax As Variant
Funcion As String
LimAplicInf As Variant
LimAplicSup As Variant
LimAplicReal As Variant
Funcion = "F8"
'Considero como primera aproximación de salto neto, el caudal resultante para la
media ponderada de los límites de rango
CorteCurva = 0.5 * (HnMin + HnMax)
'Interpolación simple
Call BuscaHorquilla(Central, Funcion, HorqMin, HorqMax, CorteCurva, LimAplicInf,
LimAplicSup)
Call ResultadoFcPolinom(Central, Abscisa, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, Abscisa, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax, Ordenada)
Call Interpola(HorqMin, HorqMax, CorteCurva, LimAplicInf, LimAplicSup,
LimAplicReal)
'Compruebo si el usuario ha introducido una Abscisa mayor que el LimAplicReal
(interpolado)
If Abscisa < LimAplicReal Then
QInic = Ordenada
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
175
Else
'El límite de aplicación real (interpolado) es inferior a la abscisa que ha
introducido, por lo que es el valor que se ha usado al hacer el cálculo
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMin, Funcion, OrdenadaMin)
Call ResultadoFcPolinom(Central, LimAplicReal, HorqMax, Funcion, OrdenadaMax)
Call Interpola(HorqMin, HorqMax, CorteCurva, OrdenadaMin, OrdenadaMax,
Ordenada)
QInic = Ordenada
End If
End Sub
D.11 Subrutinas de carga y borrado de gráficas del embalse o de la central
Sub Grafica()
Const NFc = 10
Dim HojasCentrales() As String
Dim Funciones() As String
Dim CeldaGraf() As String
Dim NombreCentral As String
Dim IndCentral As Integer
Dim Ubicacion As String
ReDim HojasCentrales(1 To NFc)
ReDim Funciones(1 To NFc)
ReDim CeldaGraf(1 To NFc)
'Vector que apunta a diferentes funciones
HojasCentrales(1) = "Figuras F3\"
HojasCentrales(2) = "Figuras F4\"
HojasCentrales(3) = "Figuras F5\"
HojasCentrales(4) = "Figuras F6\"
HojasCentrales(5) = "Figuras F7\"
HojasCentrales(6) = "Figuras F8\"
HojasCentrales(7) = "Figuras F9\"
HojasCentrales(8) = "Figuras F10\"
HojasCentrales(9) = "Figuras Q - Rendimiento\"
HojasCentrales(10) = "Figuras Colinas Rendimiento\"
Funciones(1) = "_F3"
Funciones(2) = "_F4"
Funciones(3) = "_F5"
Funciones(4) = "_F6"
Funciones(5) = "_F7"
Funciones(6) = "_F8"
Funciones(7) = "_F9"
Funciones(8) = "_F10"
Funciones(9) = "_Q-Rendimiento"
Funciones(10) = "_ColinaRendimiento"
CeldaGraf(1) = "A10"
CeldaGraf(2) = "A117"
CeldaGraf(3) = "A171"
CeldaGraf(4) = "A225"
CeldaGraf(5) = "A279"
CeldaGraf(6) = "A334"
CeldaGraf(7) = "A389"
CeldaGraf(8) = "A446"
CeldaGraf(9) = "A503"
CeldaGraf(10) = "Q503"
NombreCentral = Cells(1, 1).Value
'Necesito índice de la central
Call BuscaCentral(NombreCentral, IndCentral)
ActiveWorkbook.Sheets("Gráficas central").Activate
ActiveSheet.Cells(1, 15).Value = IndCentral 'Necesario para entrar en el if al
hacer borrar las imágenes
Ubicacion = ActiveSheet.Cells(2, 15).Value 'Necesario para cargar imágenes
For Cont = 1 To 6
ActiveSheet.Range(CeldaGraf(Cont)).Select
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
176
ActiveSheet.Pictures.Insert( _
Ubicacion & "\Figuras obtenidas con Matlab\" & HojasCentrales(Cont) &
IndCentral & Funciones(Cont) & ".jpg" _
).Select
Selection.Name = "Foto" & Cont ' Necesario para borrar las fotos
Next Cont
'Sólo entra si central bombea
If (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral =
11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Then
For Cont = 7 To 8
ActiveSheet.Range(CeldaGraf(Cont)).Select
ActiveSheet.Pictures.Insert( _
Ubicacion & "\Figuras obtenidas con Matlab\" & HojasCentrales(Cont) &
IndCentral & Funciones(Cont) & ".jpg" _
).Select
Selection.Name = "Foto" & Cont 'Necesario para borrar las fotos
Next Cont
End If
'Añadido de rendimiento
For Cont = 9 To 10
ActiveSheet.Range(CeldaGraf(Cont)).Select
ActiveSheet.Pictures.Insert( _
Ubicacion & "\Figuras obtenidas con Matlab\" & HojasCentrales(Cont) &
IndCentral & Funciones(Cont) & ".jpg" _
).Select
Selection.Name = "Foto" & Cont 'Necesario para borrar las fotos
Next Cont
ActiveSheet.Range("A10").Select
End Sub
Private Sub CommandButton1_Click()
Dim IndCentral As Integer
IndCentral = Cells(1, 15).Value
ActiveSheet.Shapes("Foto1").Select
Selection.Delete
ActiveSheet.Shapes("Foto2").Select
Selection.Delete
ActiveSheet.Shapes("Foto3").Select
Selection.Delete
ActiveSheet.Shapes("Foto4").Select
Selection.Delete
ActiveSheet.Shapes("Foto5").Select
Selection.Delete
ActiveSheet.Shapes("Foto6").Select
Selection.Delete
'Sólo entra si central bombea
If (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral =
11) Or (IndCentral = 11) Or (IndCentral = 11) Or (IndCentral = 11) Then
ActiveSheet.Shapes("Foto7").Select
Selection.Delete
ActiveSheet.Shapes("Foto8").Select
Selection.Delete
End If
ActiveSheet.Shapes("Foto9").Select
Selection.Delete
ActiveSheet.Shapes("Foto10").Select
Selection.Delete
ActiveWorkbook.Sheets("Datos central").Activate
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
177
End Sub
Sub GraficaEmb()
Const NFc = 2
Dim HojasEmbalses() As String
Dim Funciones() As String
Dim CeldaGraf() As String
Dim NombreEmbalse As String
Dim IndEmbalse As Integer
Dim Ubicacion As String
ReDim HojasEmbalses(1 To NFc)
ReDim Funciones(1 To NFc)
ReDim CeldaGraf(1 To NFc)
'Vector que apunta a diferentes funciones
HojasEmbalses(1) = "Figuras F1 y F2\"
HojasEmbalses(2) = "Figuras F1 Inversa\"
Funciones(1) = "_F1"
Funciones(2) = "_InvF1"
CeldaGraf(1) = "A7"
CeldaGraf(2) = "A117"
NombreEmbalse = Cells(1, 1).Value
'Necesito índice del embalse
Call BuscaEmbalse(NombreEmbalse, IndEmbalse)
ActiveWorkbook.Sheets("Gráficas embalse").Activate
Ubicacion = ActiveSheet.Cells(5, 10).Value 'Necesario para cargar imágenes
For Cont = 1 To NFc
ActiveSheet.Range(CeldaGraf(Cont)).Select
ActiveSheet.Pictures.Insert( _
Ubicacion & "\Figuras obtenidas con Matlab\" & HojasEmbalses(Cont) &
IndEmbalse & Funciones(Cont) & ".jpg" _
).Select
Selection.Name = "Foto" & Cont ' Necesario para borrar las fotos
Next Cont
ActiveSheet.Range("A7").Select
End Sub
Private Sub CommandButton1_Click()
ActiveSheet.Shapes("Foto1").Select
Selection.Delete
ActiveSheet.Shapes("Foto2").Select
Selection.Delete
ActiveWorkbook.Sheets("Datos embalse").Activate
End Sub
D.12 Actualización de rangos de celda a los que hacen referencia los menús
desplegables
Sub ActualizaRangoCentrales()
'Declaración de variables
Dim numFilas As Integer
Dim numFilasBorrar As Integer
Const NumCuencas = 4
Dim MatrizCuencas(1 To 2, 1 To NumCuencas) As String
Dim Cont As Integer
'Relleno el vector de
MatrizCuencas(1, 1) =
MatrizCuencas(1, 2) =
MatrizCuencas(1, 3) =
MatrizCuencas(1, 4) =
cuencas
"EBRO"
"SIL"
"TAJO"
"DUERO"
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
MatrizCuencas(2,
MatrizCuencas(2,
MatrizCuencas(2,
MatrizCuencas(2,
1)
2)
3)
4)
=
=
=
=
178
"CentralesEbro"
"CentralesSil"
"CentralesTajo"
"CentralesDuero"
'Autoborrado (en el caso de que haya algo que borrar)
For Cont = 1 To NumCuencas
ActiveSheet.Cells.Find(MatrizCuencas(2, Cont)).Offset(1, 0).Select
If Not IsEmpty(ActiveCell) Then
numFilasBorrar = Selection.CurrentRegion.Rows.Count
Range(Selection, Selection.Offset(numFilasBorrar, 0)).Select
Selection.ClearContents
End If
Next Cont
'Actualizo los nombres de los rangos de embalses de cada cuenca
For Cont = 1 To NumCuencas
'Hago filtro de la cuenca copiando los embalses
Selection.AutoFilter Field:=3, Criteria1:=MatrizCuencas(1, Cont)
Cells.Find("Central").Select
numFilas = Selection.CurrentRegion.Rows.Count
Range(Selection.Offset(1, 0), Selection.Offset(numFilas - 1, 0)).Select
Selection.Copy
'Copia abajo para darle nombre al rango
ActiveSheet.Cells.Find(MatrizCuencas(2, Cont)).Offset(1, 0).Select
ActiveSheet.Paste
ActiveWorkbook.Names.Add Name:=MatrizCuencas(2, Cont),
RefersToR1C1:=Selection
Next Cont
'Dejo la tabla sin ningún tipo de autofiltro (para que no se quede con el filtro
de la última cuenca
Selection.AutoFilter Field:=3
'No olvido crear un rango para todas las centrales
ActiveSheet.Cells.Find("Central").Offset(1, 0).Select
numFilas = Selection.CurrentRegion.Rows.Count
Range(Selection, Selection.Offset(numFilas - 2, 0)).Select
ActiveWorkbook.Names.Add Name:="Centrales", RefersToR1C1:=Selection
Sheets("Duero").ComboCentralesDuero.ListFillRange = "CentralesDuero"
Sheets("Ebro").ComboCentralesEbro.ListFillRange = "CentralesEbro"
Sheets("Sil").ComboCentralesSil.ListFillRange = "CentralesSil"
Sheets("Tajo").ComboCentralesTajo.ListFillRange = "CentralesTajo"
End Sub
Sub ActualizaRangoEmbalses()
'Declaración de variables
Dim numFilas As Integer
Dim numFilasBorrar As Integer
Const NumCuencas = 5
Dim MatrizCuencas(1 To 2, 1 To NumCuencas) As String
Dim Cont As Integer
'Relleno el vector de
MatrizCuencas(1, 1) =
MatrizCuencas(1, 2) =
MatrizCuencas(1, 3) =
MatrizCuencas(1, 4) =
MatrizCuencas(1, 5) =
MatrizCuencas(2, 1) =
MatrizCuencas(2, 2) =
MatrizCuencas(2, 3) =
MatrizCuencas(2, 4) =
cuencas
"EBRO"
"SIL"
"TAJO"
"DUERO"
"JÚCAR"
"EmbalsesEbro"
"EmbalsesSil"
"EmbalsesTajo"
"EmbalsesDuero"
D Desarrollo de interfaces y realización de cálculos en Excel mediante programación en VBA
179
MatrizCuencas(2, 5) = "EmbalsesJucar"
'Autoborrado (en el caso de que haya algo que borrar)
For Cont = 1 To NumCuencas
ActiveSheet.Cells.Find(MatrizCuencas(2, Cont)).Offset(1, 0).Select
If Not IsEmpty(ActiveCell) Then
numFilasBorrar = Selection.CurrentRegion.Rows.Count
Range(Selection, Selection.Offset(numFilasBorrar, 0)).Select
Selection.ClearContents
End If
Next Cont
'Actualizo los nombres de los rangos de embalses de cada cuenca
For Cont = 1 To NumCuencas
'Hago filtro de la cuenca copiando los embalses
Selection.AutoFilter Field:=3, Criteria1:=MatrizCuencas(1, Cont)
Cells.Find("Embalse").Select
numFilas = Selection.CurrentRegion.Rows.Count
Range(Selection.Offset(1, 0), Selection.Offset(numFilas - 1, 0)).Select
Selection.Copy
'Copia abajo para darle nombre al rango
ActiveSheet.Cells.Find(MatrizCuencas(2, Cont)).Offset(1, 0).Select
ActiveSheet.Paste
ActiveWorkbook.Names.Add Name:=MatrizCuencas(2, Cont),
RefersToR1C1:=Selection
Next Cont
'Dejo la tabla sin ningún tipo de autofiltro (para que no se quede con el filtro
de la última cuenca
Selection.AutoFilter Field:=3
'No olvido crear un rango para todos los embalses
ActiveSheet.Cells.Find("Embalse").Offset(1, 0).Select
numFilas = Selection.CurrentRegion.Rows.Count
Range(Selection, Selection.Offset(numFilas - 2, 0)).Select
ActiveWorkbook.Names.Add Name:="Embalses", RefersToR1C1:=Selection
Sheets("Duero").ComboEmbalsesDuero.ListFillRange = "EmbalsesDuero"
Sheets("Júcar").ComboEmbalsesJucar.ListFillRange = "EmbalsesJucar"
Sheets("Ebro").ComboEmbalsesEbro.ListFillRange = "EmbalsesEbro"
Sheets("Sil").ComboEmbalsesSil.ListFillRange = "EmbalsesSil"
Sheets("Tajo").ComboEmbalsesTajo.ListFillRange = "EmbalsesTajo"
End Sub
E
Ampliaciones que contiene la
herramienta CARHI
E Ampliaciones que contiene la herramienta CARHI
E.1
Función que relaciona el caudal por grupo con el rendimiento de la turbina
%%
%Autor: Juan Palomares
%Caudal - Rendimiento
%%
function CaudalRendimiento()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de centrales (col2)
% y sus respectivos índices (col3)
load Centrales
%Cargo Caudal: col1=NCurvas col2 = índice central, col3 = índice curvas,
%col4 = VLIM, col5 = salto neto, col6 = ruido y col7 - col10 coef en orden
%[coef0,...,coefn]
load Caudal
%Cargo leyenda: número de grupos
load Leyenda
%Cargo coefientes (col2-col4) para hallar caudal máximo para un salto neto
load CoefHnQmax
%%
%Número de centrales
NCurvas = length(Caudal);
%Número de puntos que pintaré
NPuntos = 1000;
%Matriz de coeficientes
Cambio = 0;
for CfCt =1: NCurvas
%Pongo índices para luego saber cuántas curvas pongo en cada gráfica
if Caudal(CfCt,3) == 1
Cambio = Cambio + 1;
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
else
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
end
end
%Necesito el orden: coefn, coef(n-1),...,coef0] para usar polyval
Coef= fliplr(Coef);
%%
%Genero un vector con los caudales máximos para el salto neto al que se
%corresponde cada curva
for CfCt = 1:NCurvas
Qmax(CfCt,1) = polyval(CoefHnQmax(Caudal(CfCt,2),2:4),Caudal(CfCt,5));
end
%Matriz de abscisas
for CfCt =1: NCurvas
xt(CfCt,1:NPuntos) = linspace(0.4*Qmax(CfCt,1),Qmax(CfCt,1),NPuntos);
end
%Matriz de ordenadas en potencias
for CfCt =1: NCurvas
yt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
end
%Matriz de ordenadas en rendimientos
for CfCt=1:NCurvas
yt(CfCt,1:NPuntos) =
yt(CfCt,1:NPuntos).*1000000./9800./Caudal(CfCt,5)./xt(CfCt,1:NPuntos);
%No pinto el rendimiento total, sino el rendimiento de la turbina que es
%el rendimiento total entre el rendimiento del alternador (=0.98)
yt(CfCt,1:NPuntos) = yt(CfCt,1:NPuntos)/0.98;
end
%%
%Gráficas
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = 1;
Cont = 0;
for CfTotCt =1: NCurvas
%Uso índices para saber cuántas curvas pongo en cada gráfica
if Coef(CfTotCt,1) ~= Antiguo
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',15);
ylabel('Rendimiento de la turbina','FontSize',15);
PrimLeyenda = CfTotCt - Cont;
UltLeyenda = CfTotCt - 1;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','Best');
NbArchivo = strcat(num2str(Antiguo),'_Q-Rendimiento');
saveas(gcf,NbArchivo,'jpeg');
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
Antiguo = Coef(CfTotCt,1);
Cont = 0;
end
Cont = Cont + 1;
if Cont == 1
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'g');
else
if Cont == 2
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'b');
else
if Cont == 3
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'k');
else
if Cont == 4
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'r');
else
if Cont == 5
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'c');
else
if Cont == 6
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'m');
else
if Cont == 7
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'y');
else
if Cont == 8
plot (xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'-g');
else
if Cont == 9
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'--b');
else
if Cont == 10
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'--y');
else
if Cont == 11
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'ob');
else
if Cont ==12
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'ok');
else
if Cont ==13
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'or');
else
if Cont ==14
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'oc');
else
if Cont ==15
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'om');
else
if Cont ==16
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'oy');
else
if Cont==17
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'xy');
else
plot
(xt(CfTotCt,1:NPuntos),yt(CfTotCt,1:NPuntos),'xb');
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',15);
ylabel('Rendimiento de la turbina','FontSize',15);
PrimLeyenda = CfTotCt - Cont;
UltLeyenda = CfTotCt - 1;
legend(Leyenda(PrimLeyenda:UltLeyenda),'Location','Best');
NbArchivo = strcat(num2str(Antiguo),'_Q-Rendimiento');
saveas(gcf,NbArchivo,'jpeg');
return
E.2
Colinas de rendimiento: relación entre el salto neto, el caudal por grupo y el
rendimiento de la turbina
%%
%Autor: Juan Palomares
%Caudal - Salto Neto - Rendimiento
%%
function ColinasRendimiento()
%Inicializo
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de centrales (col2)
% y sus respectivos índices (col3)
load Centrales
%Cargo Caudal: col1=NCurvas col2 = índice central, col3 = índice curvas,
%col4 = VLIM, col5 = salto neto, col6 = ruido y col7 - col10 coef en orden
%[coef0,...,coefn]
load Caudal
%Cargo coefientes (col2-col4) para hallar caudal máximo para un salto neto
load CoefHnQmax
%%
%Número de centrales
NCurvas = length(Caudal);
%Número de puntos que pintaré
NPuntos = 100;
%Matriz de coeficientes
Cambio = 0;
for CfCt =1: NCurvas
%Pongo índices para luego saber cuántas curvas pongo en cada gráfica
if Caudal(CfCt,3) == 1
Cambio = Cambio + 1;
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
else
Coef(CfCt,5) = Cambio;
Coef(CfCt,1:4) = Caudal(CfCt,7:10);
end
end
%Necesito el orden: coefn, coef(n-1),...,coef0] para usar polyval
Coef= fliplr(Coef);
%%
%Genero un vector con los caudales máximos para el salto neto al que se
%corresponde cada curva
for CfCt = 1:NCurvas
Qmax(CfCt,1) = polyval(CoefHnQmax(Caudal(CfCt,2),2:4),Caudal(CfCt,5));
end
%Matriz de abscisas en caudales
for CfCt =1: NCurvas
xt(CfCt,1:NPuntos) = linspace(0.4*Qmax(CfCt,1),Qmax(CfCt,1),NPuntos);
end
%Matriz de zs en potencias
for CfCt =1: NCurvas
zt(CfCt,1:NPuntos)= polyval(Coef(CfCt,2:5),xt(CfCt,1:NPuntos));
end
%Matriz de zs en rendimientos
for CfCt=1:NCurvas
zt(CfCt,1:NPuntos) =
zt(CfCt,1:NPuntos).*1000000./9800./Caudal(CfCt,5)./xt(CfCt,1:NPuntos);
%No pinto el rendimiento total, sino el rendimiento de la turbina que es
%el rendimiento total entre el rendimiento del alternador (=0.98)
zt(CfCt,1:NPuntos) = zt(CfCt,1:NPuntos)/0.98;
end
%Creo el meshgrid
Cont = 0;
Antiguo = 1;
for CfTotCt =1: NCurvas
%Uso índices para saber cuándo he acabado con central (cuando entro en
%el if, Cont=número curvas central, CfTotCt=primera curva siguiente
%central y Antiguo=número de la central en cuestión)
if Coef(CfTotCt,1) ~= Antiguo
y(Antiguo,1:NPuntos) = linspace(Caudal(CfTotCt-Cont,5),Caudal(CfTotCt 1,5),NPuntos);
[X Y]= meshgrid(xt(CfTotCt - 1,1:NPuntos),y(Antiguo,1:NPuntos));
%Cuando sólo hay una curva (Chandreja y Pontenovo, que son depósitos),
%no me deja pintarlo, así que me los salto
if Cont ~= 1
Z = interp2(xt(CfTotCt - 1,1:NPuntos),Caudal((CfTotCt - Cont:CfTotCt1),5),zt((CfTotCt - Cont:CfTotCt-1),1:NPuntos),X,Y);
Antiguo = Coef(CfTotCt,1);
Cont = 0;
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
subplot(1,2,1);
meshc(X,Y,Z);
title (Centrales(Antiguo - 1,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',12);
ylabel('Salto neto (m)','FontSize',12);
zlabel('Rendimiento','FontSize',12);
subplot(1,2,2);
contour (X,Y,Z);
title('Curvas de nivel','Fontsize',15);
xlabel ('Caudal (m^{3}/s)','FontSize',12);
ylabel('Salto neto (m)','FontSize',12);
NbArchivo = strcat(num2str(Antiguo),'_ColinaRendimiento');
saveas(gcf,NbArchivo,'jpeg');
else
Antiguo = Coef(CfTotCt,1);
Cont = 0;
end
end
Cont = Cont + 1;
end
y(Antiguo,1:NPuntos) = linspace(Caudal(CfTotCt-Cont,5),Caudal(CfTotCt - 1,5),NPuntos);
[X Y]= meshgrid(xt(CfTotCt - 1,1:NPuntos),y(Antiguo,1:NPuntos));
Z = interp2(xt(CfTotCt - 1,1:NPuntos),Caudal((CfTotCt - Cont:CfTotCt-1),5),zt((CfTotCt Cont:CfTotCt-1),1:NPuntos),X,Y);
Antiguo = Coef(CfTotCt,1);
Cont = 0;
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
subplot(1,2,1);
meshc(X,Y,Z);
title (Centrales(Antiguo,2),'FontSize',17);
xlabel ('Caudal (m^{3}/s)','FontSize',12);
ylabel('Salto neto (m)','FontSize',12);
zlabel('Rendimiento','FontSize',12);
subplot(1,2,2);
contour (X,Y,Z);
title('Curvas de nivel','Fontsize',15);
xlabel ('Caudal (m^{3}/s)','FontSize',12);
ylabel('Salto neto (m)','FontSize',12);
NbArchivo = strcat(num2str(Antiguo),'_ColinaRendimiento');
saveas(gcf,NbArchivo,'jpeg');
return
E.3
Ajuste de la función volumen útil - cota mediante el uso de splines
%%
%Autor: Juan Palomares
%Aproximación de la función inversa de la función cota - volumen útil
%%
function Spline()
%Inicializo
format long
close all
clear all
clc
%Cargo matriz con nombre de cuencas (col1), nombre de embalses (col2)
% y sus respectivos índices (col3)
load Embalse
%cargo volumen de todos los embalses
load Volumenes
%cargo cota de todos los embalses
load Cotas
%%
%Número de embalses
NEmbalses = size(Volumenes,1);
%Número de elementos
NElem = size(Volumenes,2);
%Variable para generar matriz de coeficientes
Antiguo = 1;
for Cont = 1:NEmbalses
%Primera aproximación de spline cúbica (pasa por los extremos)
xp(Cont,1:2) = [Volumenes(Cont,1) Volumenes(Cont,NElem)];
yp(Cont,1:2) = [Cotas(Cont,1) Cotas(Cont,NElem)];
EstrSpline = spline(xp(Cont,1:2), yp(Cont,1:2));
%Vector de desvios en valor absoluto
Desvio(Cont,1:NElem) = abs(Cotas(Cont,1:NElem) - ppval(EstrSpline,
Volumenes(Cont,1:NElem)));
MaxDesvio = max(Desvio(Cont,1:NElem));
NTramos(Cont,1) = 1;
%Iteración para determinar el número de tramos
while (MaxDesvio >= 0.03)
%Divido en tramos
PosicionDesvio = find(Desvio(Cont,1:NElem) >= MaxDesvio);
xp(Cont,NTramos(Cont,1) + 2) = Volumenes(Cont,PosicionDesvio);
xp(Cont,1:NTramos(Cont,1) + 2) = sort(xp(Cont,1:NTramos(Cont,1) + 2));
yp (Cont,NTramos(Cont,1) + 2)= Cotas(Cont,PosicionDesvio);
yp(Cont,1:NTramos(Cont,1) + 2) = sort(yp(Cont,1:NTramos(Cont,1) + 2));
%Hago pasar la spline por puntos que determinan los tramos
EstrSpline = spline(xp(Cont,1:NTramos(Cont,1) + 2), yp(Cont,1:NTramos(Cont,1) +
2));
Desvio(Cont,1:NElem) = abs(Cotas (Cont,1:NElem)- ppval(EstrSpline,
Volumenes(Cont,1:NElem)));
MaxDesvio = max(Desvio(Cont,1:NElem));
NTramos(Cont,1) = NTramos(Cont,1) + 1;
end
%Copio los coeficientes de la spline de tercer grado
[v,coef,n,o,d] = unmkpp(EstrSpline);
%A veces spline no "usa" tantos tramos o no genera 4 coef
NTramosSpline = size(coef,1);
NCoefSpline = size(coef,2);
Coef(Antiguo:Antiguo + NTramosSpline - 1,1:NCoefSpline) = coef;
Coef(Antiguo:Antiguo + NTramosSpline - 1,5) = Cont;
Antiguo = Antiguo + NTramosSpline;
%Dibujo spline encima de función inversa
fullscreen = get(0,'ScreenSize');
figure('Position',[10 -80 fullscreen(3) fullscreen(4)]);
hold
title (Embalse(Cont,2),'FontSize',17);
xlabel('Volumen útil (hm^{3})','FontSize',15);
ylabel ('Cota (msnm)', 'FontSize',15);
plot (Volumenes(Cont,1:NElem),Cotas(Cont,1:NElem),'b');
plot(xp(Cont,1:NTramos(Cont,1) + 1),yp(Cont,1:NTramos(Cont,1) + 1),'o');
plot(Volumenes(Cont,1:NElem),ppval(EstrSpline,Volumenes(Cont,1:NElem)),'r');
legend('Función inversa','Puntos por donde pasa spline','Spline','Location','B');
NbArchivo = strcat(num2str(Cont),'_InvF1');
saveas(gcf,NbArchivo,'jpeg');
%Inicializo la estructura Spline y el número de tramos
clear EstrSpline
NTramos(Cont,1) = NTramosSpline;
end
return