SISTEMAS DE AMORTIZACIONES
Anuncio
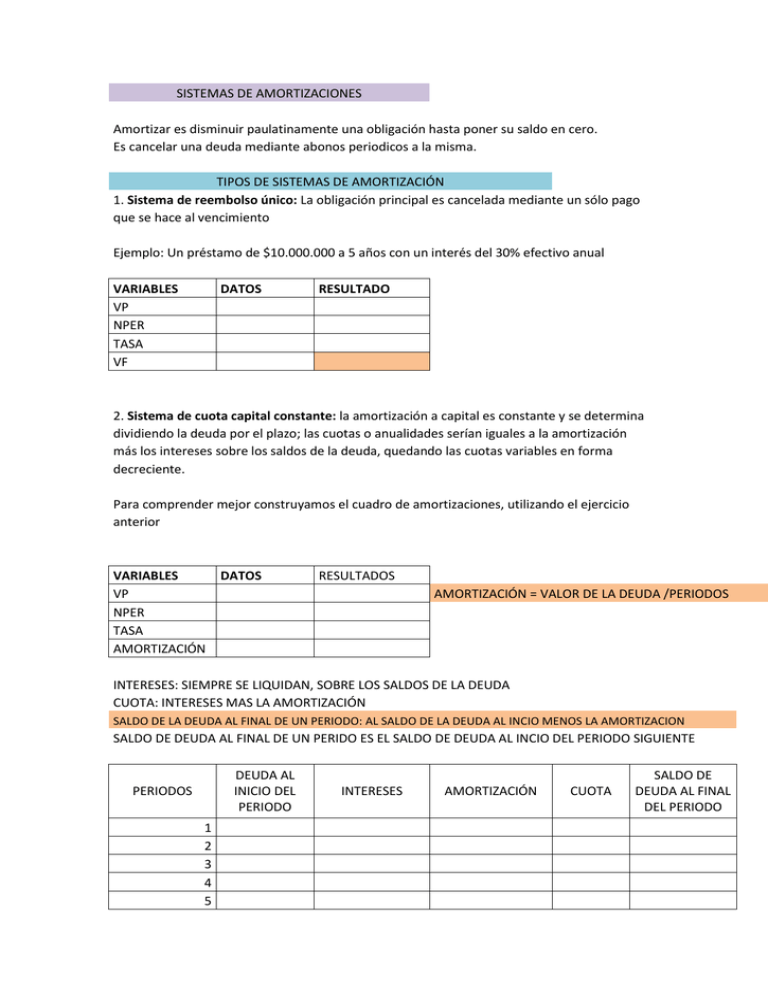
SISTEMAS DE AMORTIZACIONES Amortizar es disminuir paulatinamente una obligación hasta poner su saldo en cero. Es cancelar una deuda mediante abonos periodicos a la misma. TIPOS DE SISTEMAS DE AMORTIZACIÓN 1. Sistema de reembolso único: La obligación principal es cancelada mediante un sólo pago que se hace al vencimiento Ejemplo: Un préstamo de $10.000.000 a 5 años con un interés del 30% efectivo anual VARIABLES VP NPER TASA VF DATOS RESULTADO 2. Sistema de cuota capital constante: la amortización a capital es constante y se determina dividiendo la deuda por el plazo; las cuotas o anualidades serían iguales a la amortización más los intereses sobre los saldos de la deuda, quedando las cuotas variables en forma decreciente. Para comprender mejor construyamos el cuadro de amortizaciones, utilizando el ejercicio anterior VARIABLES VP NPER TASA AMORTIZACIÓN DATOS RESULTADOS AMORTIZACIÓN = VALOR DE LA DEUDA /PERIODOS INTERESES: SIEMPRE SE LIQUIDAN, SOBRE LOS SALDOS DE LA DEUDA CUOTA: INTERESES MAS LA AMORTIZACIÓN SALDO DE LA DEUDA AL FINAL DE UN PERIODO: AL SALDO DE LA DEUDA AL INCIO MENOS LA AMORTIZACION SALDO DE DEUDA AL FINAL DE UN PERIDO ES EL SALDO DE DEUDA AL INCIO DEL PERIODO SIGUIENTE DEUDA AL INICIO DEL PERIODO PERIODOS 1 2 3 4 5 INTERESES AMORTIZACIÓN CUOTA SALDO DE DEUDA AL FINAL DEL PERIODO En algunos casos se requiere conocer los intereses, la cuota o el saldo de la deuda en un periodo cualquiera, entonces utilizamos: FORMULA 1 FORMULA 2 FORMULA 3 FORMULA 4 FORMULAS DE CUOTA CAPITAL CONSTANTE Amortizacion real del periodo A = VP/n Intereses en el primer periodo I1 = VP *i Intereses en el periodo K Ik = I1(1 -(k/n)) Cuota a pagar en el periodo K CK = A + IK siendo K = k-1 saldo de deuda final del periodo K FORMULA 5 SDFK= PV (1 -(K/N)) Encontremos los intereses del primer periodo I1 encontremos los intereses del 4 año I4 cual sera el saldo de deuda al finalizarnel tercer año SDFK 3. SISTEMA DE CUOTA FIJA: se determina una cuota fija para todo el plazo, y en ella se incluye: la amortización a capital y los intereses sobre el saldo de la deuda Para nuestro ejemplo VARIABLES VP NPER TASA CUOTA DATOS DEUDA AL INICIO DEL PERIODO PERIODOS 1 2 3 4 5 RESULTADO INTERESES AMORTIZACIÓN CUOTA SALDO DE DEUDA AL FINAL DEL PERIODO FORMULA 1 FORMULA 2 VARIABLE CUOTA Interes en periodo K FUNCION EN EXCEL PAGO PAGOINT FORMULA 3 Amortización PAGOPRINT en el periodo k FORMULA 4 Intereses pagados entre periodos FORMULA 5 Amortizaciones pagadas entre PAGO.PRIN.ENTRE periodos FORMULA 6 Saldo de deuda Ik= VP*i A1((1+i)^(k-1) - 1) AK= A1*(1+i)^(k-1) PAGO.INT-ENTRE SDK = VP- A1* ((1+i)^k - 1))/i Intereses y la amortización en el periodo 3 PAGOINT PAGOPRINT Intereses pagados entre el periodo 2 y 4 PAGO.INT.ENTRE EJERCICIO Una propiedad de $15.000.000 es financiada a 15 años, para amortizarla con cuotas mensuales iguales, pagando un interes del 2,5% mensual, se desea saber Cuota a pagar cada mes? Determina la amortización real, los intereses y el saldo de deuda al finalizar del mes 70