Empieza a Leer

1850-1930
sección i
1
N
O
E
S
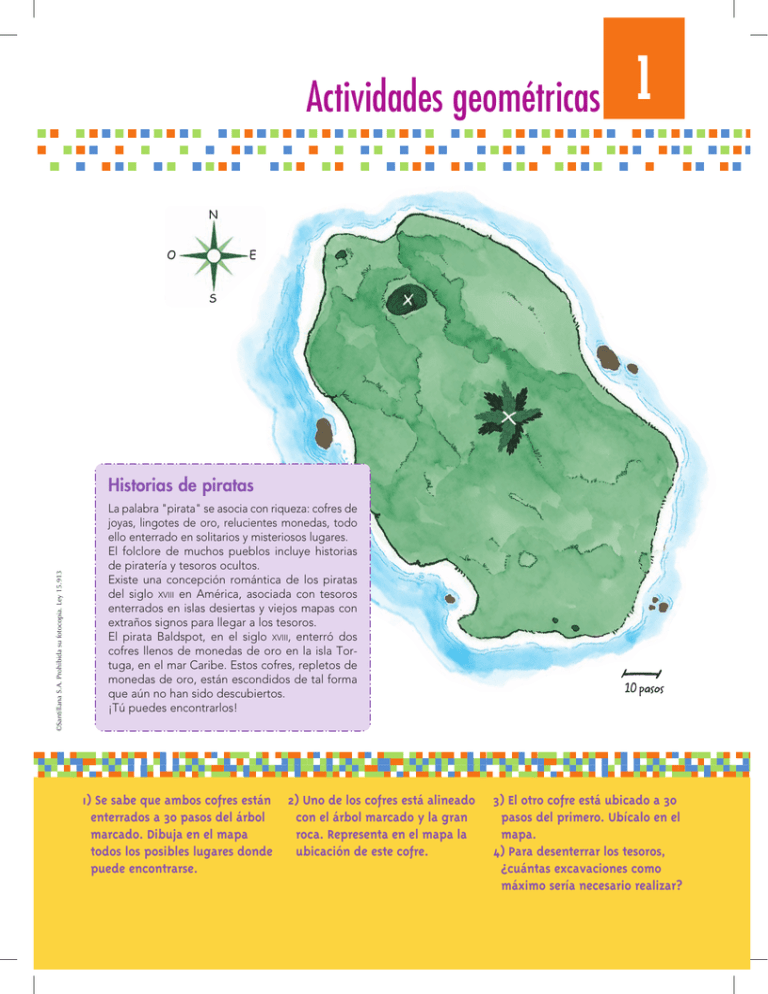
Historias de piratas
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
ura 2
Actividades geométricas
La palabra "pirata" se asocia con riqueza: cofres de
joyas, lingotes de oro, relucientes monedas, todo
ello enterrado en solitarios y misteriosos lugares.
El folclore de muchos pueblos incluye historias
de piratería y tesoros ocultos.
Existe una concepción romántica de los piratas
del siglo xviii en América, asociada con tesoros
enterrados en islas desiertas y viejos mapas con
extraños signos para llegar a los tesoros.
El pirata Baldspot, en el siglo xviii, enterró dos
cofres llenos de monedas de oro en la isla Tor­
tuga, en el mar Caribe. Estos cofres, repletos de
monedas de oro, están escondidos de tal forma
que aún no han sido descubiertos.
¡Tú puedes encontrarlos!
1) Se sabe que ambos cofres están
enterrados a 30 pasos del árbol
marcado. Dibuja en el mapa
todos los posibles lugares donde
puede encontrarse.
2) Uno de los cofres está alineado
con el árbol marcado y la gran
roca. Representa en el mapa la
ubicación de este cofre.
3) El otro cofre está ubicado a 30
pasos del primero. Ubícalo en el
mapa.
4) Para desenterrar los tesoros,
¿cuántas excavaciones como
máximo sería necesario realizar?
10
1. Circunferencia. Círculo. Concepto de lugar geométrico
Circunferencia. Círculo
Los cofres están en puntos cuya distancia al pie del árbol marcado (punto M) es
de 30 pasos. Todos los puntos del mapa que cumplen esta propiedad pertenecen
a una figura que es una circunferencia de centro M y radio 30 pasos.
Llamaremos circunferencia de centro O y radio r
al conjunto de los puntos del plano que distan r
de O.
NotacióN: C (O, r)
r
O
Si en la actividad inicial se cambia la infor­
mación “están enterrados a 30 pasos del
árbol marcado” por “están enterrados a
30 pasos o menos del árbol marcado”,
¿cómo resolverías las partes 1), 2) y 3)?
Llamaremos círculo de centro O y radio r al con­
junto de los puntos del plano cuya distancia al
centro es menor o igual que el radio.
r
O
De acuerdo con esta definición, el círculo está formado por los puntos de la cir­
cunferencia y los puntos interiores a ella.
11
Concepto de lugar geométrico
La circunferencia es un ejemplo de lugar geométrico en el plano.
• Todo punto del plano que diste r de O pertenece a la circunferencia de centro
O y radio r.
• Todo punto de dicha circunferencia dista r de O.
Diremos que una figura F es el lugar geométrico (LG ) de los puntos que
cumplen una propiedad P si:
• Todo punto que verifica la propiedad P pertenece a F .
• Todo punto que pertenece a F cumple con la propiedad P.
Se ha representado un arco de circunferencia de
centro A y radio 2. Analiza si esta figura es el LG
de los puntos del plano que distan 2 del punto A.
Fundamenta tu respuesta.
2
3
A
2
3
A
A
fig.5
El conjunto formado por los puntos de la zona sombreada, ¿es un LG ? Explica.
fig.5
2
3
A
2
4
A
B
3
A
4
B
A
fig.5
El círculo de centro P y radio 3, ¿es el LG de los
puntos del plano que distan 3 de P? Justifica tu res­
puesta.
fig.6
fig.5
3
P
fig.6
P
P
3
a. La semicircunferencia de centro B y diámetro 3 de la figura, ¿es el LG
de los puntos del plano que distan 1,5 de B?
b. Define la semicircunferencia de diámetro 3 como un LG .
P
P
fig.7
fig.7
Q
3
B
P
3fig.7
fig.8
P
fig.7
Q
B
fig.8
P
12
El método del jardinero
A un jardinero le encargan construir tres canteros con el siguiente diseño.
eje
eje
Circunferencia
Se decide entonces a trazar dos circunferencias y una elipse.
Para trazar una circunferencia utiliza una cuerda con dos estacas anudadas en los
extremos. Clava una de ellas en la tierra y, manteniendo la cuerda tensa, surca el
terreno con la otra.
Para trazar la elipse también utiliza una cuerda con dos estacas en los extremos,
pero ahora fija ambas en la tierra. Luego surca el terreno y hace resbalar una ter­
cera estaca, siempre con la cuerda en tensión.
eje
eje
Elipse
El jardinero sabía muy bien que la elipse es el conjunto de puntos del plano cuya
suma de distancias a dos puntos fijos es constante. La elipse, al igual que la cir­
cunferencia, es un LG .
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
Las secciones
cónicas son figuras
que resultan de
la intersección de
un plano (plano
secante) con la
superficie cónica
de revolución.
13
2. Igualdad de triángulos. Criterios de igualdad
Igualdad de triángulos
C
Dos triángulos son iguales
cuando tienen sus tres lados
y sus tres ángulos respectiva­
mente iguales.
A’
B
B’
A
C’
Criterios de igualdad de triángulos
Primer criterio (LAL)
Segundo criterio (ALA)
Tercer criterio (LLL)
Dos triángulos son iguales si
tienen respectivamente iguales
dos lados y el ángulo compren­
dido por ellos.
Dos triángulos son iguales si
tienen respectivamente iguales
un lado y los dos ángulos adya­
centes a este.
Dos triángulos son iguales si
tienen respectivamente iguales
los tres lados.
P
M
R
M’
N
N’
Q
P’
S
S’
Q’
E
R’
G
F
F’
G’
E’
Aplicando los criterios de igualdad
Los criterios de igualdad son una herramienta muy útil para probar la igualdad
de dos segmentos o dos ángulos, si probamos previamente que ese par de seg­
mentos o de ángulos son elementos correspondientes de dos triángulos iguales.
Veamos un ejemplo.
^
^
En la figura adjunta se sabe que: RMS = TMS y que RM = TM
Queremos probar que: RS = TS
R


Para ello probaremos que RMS = TMS
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
^
^
RMS = TMS (dato)
RM = TM (dato)
MS común






M

⇒ RMS = TMS ⇒ RS = TS
por (LAL)
por definición de
triángulos iguales
T
Actividades
C
Se sabe que: AB = CB
AD = CD
Prueba que:
^
D
B
^
ADB = CDB
A
S
3. Mediatriz de un segmento como lugar geométrico
A ambas orillas de un río hay dos árboles, uno frente al otro. En la cima de cada
uno hay un pájaro. De pronto, los dos pájaros ven un pez que aparece en la super­
ficie del agua entre los dos árboles y se lanzan, al mismo tiempo y a la misma
velocidad, para alcanzarlo. Llegan en el mismo instante al pez. ¿En qué punto de
la superficie del agua lo alcanzan?
Como los pájaros se lanzan al mismo tiempo, a la misma velocidad y alcanzan el
pez en el mismo instante, podemos decir que las distancias recorridas son iguales.
Por lo tanto, se trata de encontrar un punto de la superficie del agua, entre los
dos árboles, que equidiste de A y de B. Los puntos que cumplen esta propiedad
pertenecen a la mediatriz del segmento AB.
Para ubicar el punto buscado
trazamos la mediatriz de AB.
Para resolver este problema utilizamos la pro­
piedad que cumplen los puntos de la media­
triz y solo ellos: estar a igual distancia de los
extremos del segmento.
A
B
Demostraremos que la mediatriz es un LG . Para ello recordaremos previamente
su definición.
La mediatriz de un segmento AB es la
recta perpendicular al segmento en su
punto medio.
NotacioN: mz(AB)
A
B
De acuerdo con el concepto de LG , debemos probar que:
1) Todo punto del plano que equidiste de los extremos de un segmento perte­
nece a su mediatriz.
2) Todo punto que pertenezca a la mediatriz de un segmento equidista de los
extremos de este.
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
14
15
1) Sea P un punto del plano que equidista de A y de B y M el punto medio del
segmento AB. Para probar que P pertenece a la mediatriz de AB demostrare­
mos que la recta PM es perpendicular al segmento AB.
Se sabe que: PA = PB y que M es el punto medio de AB.
P
Probaremos que P pertenece a la mediatriz de AB.
Para ello consideremos los triángulos AMP y BMP.




AM = MB (definición de punto medio)  ⇒ AMP = BMP ⇒
 por (LLL)
por definición de

triángulos iguales
PM común
PA = PB (dato)
^
⇒
A
M
^
AMP = BMP
B
^
^

 ⇒ AMP = BMP = 1 recto ⇒
AMP y BMP adyacentes 
^
^
⇒ PM es perpendicular al segmento AB en su punto medio ⇒ P ∈ mz(AB)
por definición de mediatriz
2) Sea P un punto de la mediatriz del segmento AB. Para probar que P equidista
de A y de B demostraremos la igualdad de los triángulos AMP y BMP.
Se sabe que: P ∈ mz(AB) y que mz(AB) ∩ AB = {M}
P
Probaremos que: PA = PB
Consideramos los triángulos AMP y BMP.
B




AMP = BMP = 1 recto (definición de mediatriz)  ⇒ AMP = BMP ⇒ PA = PB
 por (LAL)
por definición de
PM común

triángulos iguales
AM = MB (definición de mediatriz)
^
M
mz(AB)
A
^
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
De 1) y 2) se deduce que la mediatriz es un LG.
La mediatriz de un segmento es el LG de
los puntos del plano que equidistan de los
extremos del segmento.
Para construir la mediatriz con regla y compás es suficiente con
determinar dos puntos del plano que equidisten de A y de B.
P
A
mz(AB)
Q
B
16
Construcción de la perpendicular a una recta por un punto
Dada una recta r y un punto P, distinguiremos dos casos:
P∈r
P∉r
Determinamos un segmento incluido en la recta
r de modo que P sea su punto medio. Luego tra­
zamos la mediatriz de dicho segmento, que es la
perpendicular a r por P.
Determinamos dos puntos de r que equidisten
de P. La mediatriz del segmento cuyos extremos
son dichos puntos es la perpendicular buscada.
)
P
r
r
P
Circuncentro. Circunferencia circunscrita
P
Considera un triángulo PQR cualquiera.
Q
a. Traza las mediatrices de PQ y QR. Llama C al punto de
intersección de dichas mediatrices.
b. A continuación aparece la demostración de que la media­
triz de PR también pasa por C.
Deduce lo que está escrito debajo de cada papelito.
CQ = CP porque C ∈ mz(
porque C ∈ mz (QR)
CR =
)
 ⇒ CR =


R
⇒ C ∈ mz (PR)
Actividades
1) Se sabe que: AB = AD
^
B
^
BAC = DAC
A, C y E alineados
Prueba que:
a. C y E pertenecen a la mediatriz de BD.


b. BME = DCE
E
C
A
D
2) Determina elLG de los puntos del plano que son vértices de todos los triángulos isósceles de base PQ.
3) ¿Cómo hallarías el centro de una circunferencia si no lo conoces?
©Santillana S.A. Prohibida su fotocopia. Ley 15.913
Podemos afirmar entonces, que las tres mediatrices concurren en el punto C.
Este punto recibe el nombre de circuncentro del triángulo y es el centro de
la circunferencia que pasa por sus tres vértices (circunferencia circunscrita al
triángulo). Trázala.