Geometría Analítica Plana
Anuncio
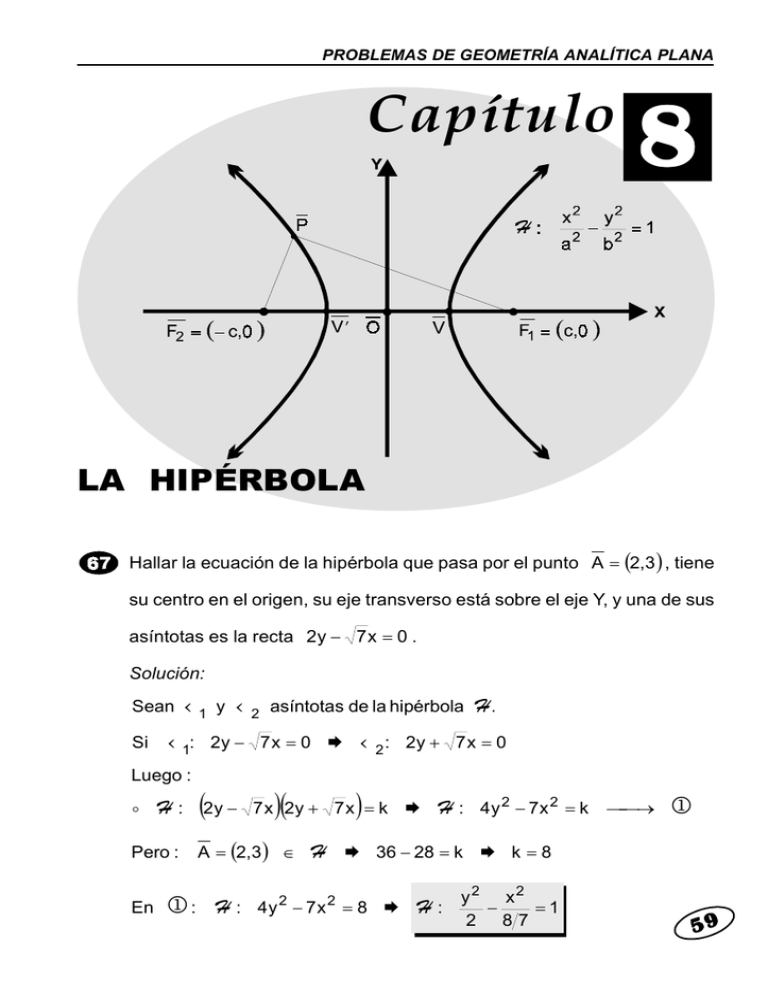
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Capítulo 8 LA HIPÉRBOLA Hallar la ecuación de la hipérbola que pasa por el punto A = (2,3 ) , tiene su centro en el origen, su eje transverso está sobre el eje Y, y una de sus asíntotas es la recta 2y − 7 x = 0 . Solución: Sean Si ‹ 1 y ‹ 2 asíntotas de la hipérbola H . ‹ 1: 2y − 7 x = 0 ! ‹ 2 : 2y + 7 x = 0 Luego : ! H : (2y − 7 x )(2y + 7 x ) = k ! H : 4y 2 − 7x 2 = k → ! Pero : En A = (2,3 ) ∈ !: H : H ! 36 − 28 = k ! k = 8 4y 2 − 7 x 2 = 8 ! H: y2 x2 − =1 2 87 59 Capítulo 8. LA HIPÉRBOLA Hallar la ecuación de la hipérbola, con vértices en V = (0,±7 ) y e = 4 3 . Solución: H: De los datos se deduce : Si : y2 a2 − x2 b2 =1 V = (0, ± 7 ) = (0, ± a ) ! a = ±7 Además : e= c 4 4 784 = ! c = × a ! c2 = a 3 3 9 Luego : b 2 = c 2 − a 2 = H: Por lo tanto : 343 784 − 49 ! b 2 = 9 9 y2 x2 − =1 49 343 9 H : 9x 2 − 7 y 2 = 343 Dada la ecuación de la hipérbola x 2 − 4 y 2 = 4 , hallar las coordenadas de los vértices y focos, las longitudes de los ejes transverso y conjugado, la excentricidad y la longitud de la cuerda normal (lado recto). Solución: H : x 2 − 4y 2 = 4 ! H : Sabemos : x2 y2 − =1 4 1 De donde : ! a 2 = 4 ! a = ±2 ! b 2 = 1 ! b = ±1 ! c 2 = a2 + b2 = 4 + 1 = 5 ! c = ± 5 Vértices : V = (± a,0 ) = (± 2,0 ) ( Focos : F = (± c,0 ) = ± 5 ,0 Excentricidad : 60 e= c a ! ) e= 5 2 PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Cuerda Normal : CN = 2b 2 2 ×1 = =1 a 2 Eje Transverso : 2a = 4 Eje Conjugado : 2b = 2 Encontrar la ecuación de la hipérbola de focos F1 = (− 1,1) y F2 = (5,1) y un vértice en V = (0,1) . Solución: 61 Capítulo 8. LA HIPÉRBOLA Sabemos : F1 F2 = 2c = 6 ! c = 3 ! c 2 = 9 ! C = (h,k ) ! Ahora : h=2 ! C = (2,1) k =1 ! a = CV = 2 ! a 2 = 4 ! c 2 = a 2 + b2 ! 9 = 4 + b2 ! b2 = 5 Por lo tanto : H: (x − h)2 − (y − k )2 =1 H: (x − 2)2 − (y − 1)2 =1 a2 4 b2 5 Determinar la ecuación de la hipérbola, sabiendo que sus focos son los puntos F1 = (3,4 ) y F2 = (3,−2 ) y su excentricidad es igual a 2. Solución: ! C = (h,k ) ! h=3 k =1 ! C = (3,1) Luego : c = F1C = CF2 = 3 9 3 c =2 ! a= ! a2 = 4 2 a 27 9 ! b2 = Sabemos que : b 2 = c 2 − a 2 = 9 − 4 4 Además : e = Por lo tanto : 62 H: (y − k )2 − (x − h)2 =1 H: (y − 1)2 − (x − 3)2 =1 a2 94 b2 27 4 PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Hallar la ecuación de la hipérbola, cuyos focos están en los vértices de la elipse: x 2 100 + y 2 64 = 1 . Y las directrices pasan por los focos de esta elipse. Solución: En la elipse : õ: x2 y2 + =1 100 64 ! a 2 = 100 ! a = ±10 ! b 2 = 64 ! b = ±8 ! b 2 = a 2 − c 2 ! c 2 = a 2 − b 2 = 100 − 64 = 36 ! c = ±6 De donde : F = (± c,0) = (± 6,0) En la hipérbola : H: x2 a2 − y2 b2 =1 Por condición del problema, obtenemos el valor de c en la hipérbola a partir del valor de a en la elipse. ! c = ±10 ! c 2 = 100 63 Capítulo 8. LA HIPÉRBOLA La ecuación de la directriz de la hipérbola : ! x=± a a2 a2 = =± ca c 10 → x=± a e ! Por condición del problema : x = c ; donde c es un valor obtenido en la elipse. Luego en !: a 2 = 60 Seguido : b 2 = a 2 − c 2 Por lo tanto : H: H: 64 ! b 2 = 100 − 60 ! b 2 = 40 x2 a2 − y2 b2 =1 x2 y2 − =1 60 100 PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Dada la ecuación de la hipérbola: (x − 4 )2 16 − y 2 128 = 1 , encontrar las coordenadas del centro, vértices y focos; la excentricidad; las ecuaciones de las directrices y asíntotas; y la longitud de la cuerda normal (lado recto). Solución: Si (x − 4)2 − H: 16 y2 = 1 → 128 ! se deduce que C = (h,k ) = (4,0 ) Además : ! a 2 = 16 ! a = ±4 ! b 2 = 128 ! b = ±8 2 ! c 2 = a 2 + b 2 = 16 + 128 = 144 ! c = ±12 Vértice : V = (h ± a,k ) = (4 ± 4,0 ) ! s: Focos : F = (h ± c,k ) = (4 ± 12,0 ) ! V1 = (8,0 ) V2 = (0,0 ) F1 = (16,0 ) F2 = (− 8,0 ) Ecuaciones de las directrices : x = h± a 4 = 4± e 3 ! x = 16 3 x=8 3 Ecuaciones de las asíntotas ; en !: 8(x − 4 ) − y − 128 = k 2 ! [2 ! ][ ] 2 (x − 4 ) + y ⋅ 2 2 (x − 4 ) − y = 0 ‹ 1: 2 2 (x − 4) + y = 0 ‹ 2 : 2 2 (x − 4) − y = 0 65 Capítulo 8. LA HIPÉRBOLA Cuerda Normal : CN = 66 2b 2 2 × 128 = = 64 = 64 a 4 PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA Hallar la ecuación de la hipérbola que pasa por los puntos A = (3,−2) y B = (7,6 ) , tiene su centro en el origen y el eje transverso coincide con el eje X. Solución: H: x2 a2 − y2 b2 =1 ! A = (3,−2) ∈ ! B = (7,6 ) ∈ De ! y H: ! ": ∴ a 49 a 2 2 − − 4 b2 36 b2 = 1 → = 1 → ! " a 2 = 4 ; b 2 = 16 5 H: Luego : 9 H: ! x2 y2 − =1 4 16 5 H : 4x 2 − 5y 2 = 16 Un observador estacionado en el punto P oye el estampido de un rifle y el golpe de la bala sobre el objetivo en el mismo instante. Demostrar que el lugar geométrico de P es una hipérbola. Solución: Sean : ! Vb : ! Vs : Velocidad del sonido Velocidad de la bala Además : e = v⋅t ! t = e v 67 Capítulo 8. LA HIPÉRBOLA Por condición del problema : De !: ! RP BP BR − = Vb Vs Vs ! RP − BP = Vs × ! RP − BP = k 68 RP BR BP = + Vs Vb Vs → BR =k Vb (Definición de hipérbola ) LQQD !





