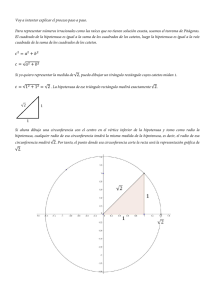
La lección de hoy es sobre Triángulos derechos
Anuncio

T.2.G.5-Jennifer Pierce-Special Right Triangles, Use the special right triangle relationships to solve problems. La lección de hoy es sobre Triángulos derechos especiales usando las relaciones de los triángulos derechos especiales para resolver problemas. El cuál es la expectativa para el aprendizaje del estudiante T.2 G 5 Hablaremos de triángulos derechos de 45, 45, 90 grados. Lado 45° Lado hipotenusa Dos de los ángulos tienen las mismas medidas. Quiere decir que los lados opuestos a ellos también son de las mismas medidas, son congruentes. Ahora la hipotenusa es √2 multiplicada por las longitudes de los lados. Si recuerdas esto, será suficiente información para resolver este problema, que usa el triangulo derecho de 45, 45, 90, grados. Veremos nuestro ejemplo: Ejemplo #1: Para el ejemplo uno vamos a buscar los valores de x y y. Y sabemos que uno de los lados es 7. X 7 45° Y Ahora sabemos que solo unos de los lados tiene valor, Recuerda: En un triangulo todos los ángulos sumaran un total de 180°. Que quiere decir, el otro lado que no tiene un valor tiene que ser 45, para que esto pueda pasar. Entonces el 7 es opuesto de 45° Angulo. Recuerda, el lado 45, 45, 90 grados triangulo siempre es congruente. Quiere decir si el lado que ya sabemos es 7 la x también es 7. ¿Cómo la hipotenusa se relaciona? La hipotenusa siempre es √2 multiplicada por la longitud del lado que ya sabemos es 7. Entonces: √2 . 7 te dará Y = 7√2 esta es la longitud de la hipotenusa. Ejemplo # 2: Para el ejemplo dos ahora la hipotenusa es el valor dado y será 10√2. ¿Cómo esta conecta con el lado? X Y 45° 10√2 Bueno, siempre será √2 multiplicado por la longitud de los lados. En este caso haremos: 10√2 = y√2 Por que la Y es uno de la longitud de los lados, Queremos resolver por Y. ¿Cómo lo haremos? Ahora mismo es y√2 para cancelar necesitas hacer lo opuesto será, dividir entre √2. Recuerda en los dos lados será: 10√2 = y √2 √2 √2 Las √2 se cancelan. Y tendrás, Y= 10 ¿Cómo busca la x? En un triangulo de 45, 45, 90 grados los lados siempre serán de la misma longitud, y son congruentes. Quiere decir si y=10, la x es igual a 10. Las dos longitudes de los dos lados del triangulo es 10. Ejemplo # 3: Es un poco difícil, aquí te dan la longitud de la hipotenusa que es 15. ¿Cómo se define la hipotenusa en un triangulo de 45, 45, 90 grados? Sera √2 multiplicada por la longitud de los lados. De nuevo, los lados que usamos es Y. Tenemos: 15 = √2 Para resolver por Y. Como el último problema, es multiplicar por la √2, lo opuesto de este seria dividir los dos lados entre √2, seria, Y= 15 √2 No podemos dejarlo de esta forma. Necesitamos racionalizar el denominador. Cada vez que tengas un radical en el denominador tendrás que multiplicar el numerador y el denominador por √2 y si haces esto y simplificas tendrás, 5 √2 2 Si no estás seguro de que hemos hecho, necesitas observar las lecciones con respecto a simplificar radicales antes de escuchar esta lección. Ahora sabes el valor de Y, si sabes esta necesitas recordar que los lados siempre son congruentes y si los lados son congruentes, esta respuesta también será la longitud para X. Entonces X y Y o los dos lados son 15 √2 =X 2 Ahora veremos triángulos derechos de 30, 60, 90 grados. Lado corto (lc) Lado largo 60° (LL) 30° Hipotenusa Tenemos el lado corto que esta opuesto al Angulo de 30°, el lado largo que esta opuesto al Angulo con 60°, y la hipotenusa que está cruzando el Angulo derecho. El lado largo es siempre √3 multiplicado por el lado corto (lc). La hipotenusa es siempre el doble del lado corto, o dos veces la longitud del lado corto. Recuerda esto al desarrollar nuestros ejemplos. Ejemplo #1: Busca el valor que no sabemos para este triangulo de 30, 60, 90 grados. Lc = 7 60° LL = X 30° Y Notas que la X es el lado largo, Y es la hipotenusa. ¿Cómo lo haremos? Recuerda el lado largo siempre es √3 multiplicado por el lado corto. Seria, LL =√3, Lado corto que seria, X = √3 . 7 para escribir este correctamente, el numero racional tendrá que escribirlo de primero, si haces esto tendrás, X = 7√3 esta es la longitud del lado largo. Ahora busca la hipotenusa que es Y. Recuerda, la hipotenusa siempre es 2 multiplicado por el lado corto. En este caso es: Hipotenusa = 2 . 7 Hipotenusa = 14 este es la longitud del lado que no sabemos de un triangulo de 30, 60, 90 grados. Ejemplo # 2: Ahora, busca X y Y, de nuevo. Lc = X 60° LL = 10 30° Y Aquí X es el lado corto, y Y es la hipotenusa. Nos han dado el lado más largo y su longitud es 10. ¿Cómo escribimos una proporción entre el lado largo y uno de los otros lados? Haremos el lado corto primero. Ya sabemos que el lado largo es √3 multiplicado por el lado corto, o sea, LL= √3 . Lcorto El lado largo es 10, lo sustituyes, y tendrás, 10 = √3 . X El lado corto es la variable X. Ahora queremos resolver por X y para hacer este necesitas eliminar la √3, si se multiplica haremos lo opuesto será dividir entre √3. Tendrás X= 10 √3 Pero necesitamos racionalizar. En matemáticas nunca deberás dejar un radical en el denominador. Si multiplicas el numerador y denominador por la √3, tendrás: 10√3 3 esta es la longitud del lado corto. Ahora busca lo longitud de la hipotenusa: La hipotenusa siempre es 2 veces la longitud del lado corto que hemos encontrado. Si hacemos este tendremos, Hip= 2 . Lc Sustituyes Y = 2 . 10√3 3 este nos dará un total de 20√3 3 esta es longitud del lado de la hipotenusa, y la longitud del lado que estamos buscando. Para el ejemplo #3: busca la longitud de los lados X y Y. Lc = X 60° Y 30° Hipotenusa = 24 En este ejemplo sabemos que la hipotenusa es 24 unidades de largo. El lado corto es X, y el lado largo es Y. Vamos a relacionar todo esto con el lado corto. Como sabemos la hipotenusa, la relacionaremos con el lado corto. La hipotenusa siempre es 2 multiplicado por la longitud del lado corto. Si este es cierto la, Hipotenusa = 2 . L corto ¿Cuál es la longitud de la hipotenusa? Es, 24 = 2 . X Porque X es el lado corto. ¿Cómo resuelves por X? Lo opuesto de multiplicar aquí seria dividir entre dos y recuerda tendrás que dividir los dos lados dividido entre dos, seria X = 12 este es la longitud del lado corto. Esta información nos ayudara a buscar el lado largo, este siempre es √3 multiplicado por le lado corto, entonces tendremos: LL = √3 . L corto Y = √3 . 12 sabes que el lado corto es 12 ahora sustituyes. Este √3 multiplicado por 12 es el valor de Y o la longitud del lado largo. Sabemos que el racional se escribe enfrente, seria, 12√3 esta es la longitud del lado largo. A si es que usas triangulo de 30.60, 90 grados, y 45, 45, 90 grados triángulos, para buscar los lados ausentes del triangulo dado.