2.9 Integración por sustitución trigonométrica
Anuncio
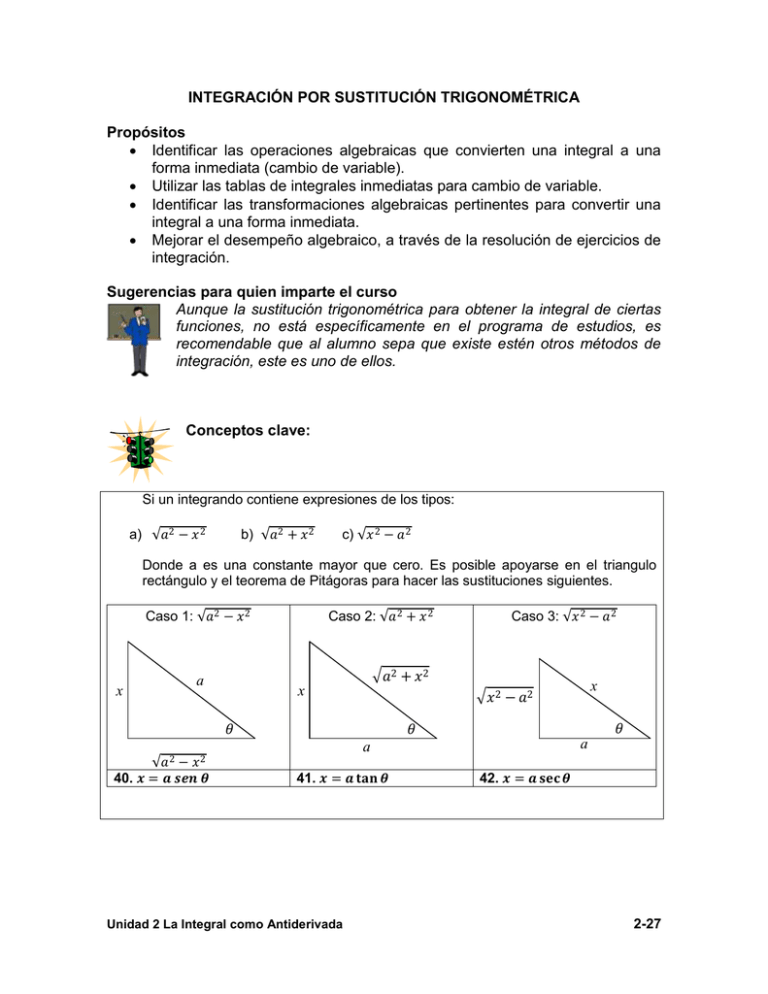
INTEGRACIÓN POR SUSTITUCIÓN TRIGONOMÉTRICA Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas para cambio de variable. Identificar las transformaciones algebraicas pertinentes para convertir una integral a una forma inmediata. Mejorar el desempeño algebraico, a través de la resolución de ejercicios de integración. Sugerencias para quien imparte el curso Aunque la sustitución trigonométrica para obtener la integral de ciertas funciones, no está específicamente en el programa de estudios, es recomendable que al alumno sepa que existe estén otros métodos de integración, este es uno de ellos. Conceptos clave: Si un integrando contiene expresiones de los tipos: a) 𝑎2 − 𝑥 2 b) 𝑎2 + 𝑥 2 c) 𝑥 2 − 𝑎2 Donde a es una constante mayor que cero. Es posible apoyarse en el triangulo rectángulo y el teorema de Pitágoras para hacer las sustituciones siguientes. Caso 2: 𝑎2 + 𝑥 2 Caso 1: 𝑎2 − 𝑥 2 x 𝑎2 + 𝑥2 a x x 𝑥2 − 𝑎2 𝜃 𝑎2 − 𝑥 2 40. 𝒙 = 𝒂 𝒔𝒆𝒏 𝜽 Caso 3: 𝑥 2 − 𝑎2 𝜃 𝜃 a a 41. 𝒙 = 𝒂 𝐭𝐚𝐧 𝜽 Unidad 2 La Integral como Antiderivada 42. 𝒙 = 𝒂 𝐬𝐞𝐜 𝜽 2-27 Puntos problemáticos Los alumnos pudieran no recordar cómo se definen las funciones trigonométricas, es recomendable que quien imparte el curso, se asegure de que los alumnos conocen lo anterior. Ejemplo 1 Obtener 1 𝑥 2 𝑎2 − 𝑥 2 𝑑𝑥 Donde 𝑎 > 0, de acuerdo con el caso 1, 𝑥 = 𝑎 𝑠𝑒𝑛 𝜃 Entonces 𝑎2 − 𝑥 2 = 𝑎2 − 𝑎2 𝑠𝑒𝑛2 𝜃 = 𝑎2 (1 − 𝑠𝑒𝑛2 𝜃) = 𝑎 1 − 𝑠𝑒𝑛2 𝜃 = 𝑎 𝑐𝑜𝑠 𝜃 Como 𝑥 = 𝑎 𝑠𝑒𝑛 𝜃. 𝑑𝑥 = 𝑎 𝑐𝑜𝑠 𝜃 𝑑𝜃. Sustituyendo en la integral 1 𝑥 2 𝑎2 − 𝑥 2 = 1 𝑎2 𝑑𝑥 = (𝑎2 𝑠𝑒𝑛2 1 1 𝑑𝜃 = (𝑠𝑒𝑛2 𝜃 ) 𝑎2 1 (𝑎𝑐𝑜𝑠 𝜃 𝑑𝜃) 𝜃 ) 𝑎 𝑐𝑜𝑠 𝜃 𝑐𝑠𝑐 2 𝜃𝑑𝜃 = − 1 𝑐𝑜𝑡𝜃 + 𝐶 𝑎2 1 Se debe regresar la integral obtenida − 𝑎 2 𝑐𝑜𝑡𝜃 + 𝐶 a la variable de integración original. Haciendo uso del triangulo del caso 1, 𝑐𝑜𝑡𝜃 = forma la integral obtenida es: 1 𝑥 2 𝑎2 − 𝑥 2 𝑑𝑥 = − 𝑎 2 −𝑥 2 𝑥 , de esta 𝑎2 − 𝑥 2 +𝐶 𝑎2 𝑥 Sugerencias para quien imparte el curso Dependiendo de las características el grupo se pudieran hacer algunos ejemplos dando un valor a la constante 𝑎, tales como 1, 4, 9, etc y después generalizarlo. 2-28 Unidad 2 La Integral como Antiderivada Ejemplo 2 Obtener 1 𝑎2 + 𝑥 2 𝑑𝑥 Donde 𝑎 > 0, de acuerdo con el caso 2, 𝑥 = 𝑎 𝑡𝑎𝑛 𝜃, por tanto 𝑑𝑥 = 𝑎 𝑠𝑒𝑐 2 𝜃 𝑑𝜃 Entonces 𝑎2 + 𝑥 2 = 𝑎2 + 𝑎2 𝑡𝑎𝑛2 𝜃 = 𝑎2 (1 + 𝑡𝑎𝑛2 𝜃) = 𝑎 1 + 𝑡𝑎𝑛2 𝜃 = 𝑎 𝑠𝑒𝑐 𝜃 Sustituyendo en la integral 1 𝑎2 + 𝑥 2 = 𝑑𝑥 = 1 (𝑎 𝑠𝑒𝑐 2 𝜃 𝑑𝜃) (𝑎 𝑠𝑒𝑐 𝜃 ) sec 𝜃 𝑑𝜃 = 𝑙𝑛 sec 𝜃 + tan 𝜃 + 𝐶 De acuerdo con el triángulo del caso 2, sec 𝜃 = = sec 𝜃 𝑑𝜃 = 𝑙𝑛 𝑎 2 +𝑥 2 𝑎 . Entonces: 𝑎2 + 𝑥 2 𝑥 + +𝐶 a 𝑎 Después de hacer algunas operaciones algebraicas, el resultado puede escribirse como: sec 𝜃 𝑑𝜃 = 𝑙𝑛 𝑎2 + 𝑥 2 + 𝑥 + 𝐶 Sugerencias para quien imparte el curso Nuevamente, dependiendo de las características el grupo, se pueden proponer algunos ejemplos dando un valor a la constante 𝑎, tales como 1, 4, 9, etc y después generalizarlo. Unidad 2 La Integral como Antiderivada 2-29 Ejemplo 3 Obtener 𝑥 2 − 𝑎2 𝑑𝑥 𝑥 Donde 𝑎 > 0, de acuerdo con el caso 3, 𝑥 = 𝑎 𝑠𝑒𝑐 𝜃, por tanto 𝑑𝑥 = 𝑎 𝑠𝑒𝑐 𝜃 tan 𝜃 𝑑𝜃 Entonces 𝑥 2 − 𝑎2 = 𝑎2 𝑠𝑒𝑐 2 𝜃 − 𝑎2 = 𝑎2 (𝑠𝑒𝑐 2 𝜃 + 1) = 𝑎 𝑡𝑎𝑛 𝜃 Sustituyendo en la integral =𝑎 𝑥 2 − 𝑎2 𝑑𝑥 = 𝑥 𝑎 𝑡𝑎𝑛 𝜃 (𝑎 𝑠𝑒𝑐 𝜃 tan 𝜃 𝑑𝜃) (𝑎 𝑠𝑒𝑐 𝜃 ) 𝑡𝑎𝑛2 𝜃 𝑑𝜃 = 𝑎 (𝑠𝑒𝑐 2 𝜃 − 1)𝑑𝜃 = 𝑎 (𝑡𝑎𝑛𝜃 − 𝜃) Como 𝑥 = 𝑎 𝑠𝑒𝑐 𝜃, entonces 𝑠𝑒𝑐 𝜃 = 𝑥 𝑎 𝑥 2 − 𝑎2 𝑑𝑥 = 𝑎 𝑥 = 2-30 y 𝜃 = 𝑠𝑒𝑐 −1 𝑥 𝑎 , entonces: 𝑥 2 − 𝑎2 𝑥 − 𝑠𝑒𝑐 −1 𝑎 𝑎 𝑥 2 − 𝑎2 − 𝑎 𝑠𝑒𝑐 −1 +𝐶 𝑥 +𝐶 𝑎 Unidad 2 La Integral como Antiderivada Ejercicios Obtén las siguientes trigonométrica 1. 2. 3. 4. 5. 6. 7. 1 𝑥 1 2+𝑥2 𝑥 9+𝑥2 𝑥 4−𝑥2 ocupando sustitución 𝑑𝑥 𝑑𝑥 𝑑𝑥 𝑥2 𝑥2 −25 𝑥2 −16 1 integrales 𝑑𝑥 𝑑𝑥 1 𝑥2 4− 𝑥2 𝑥2 9− 𝑥2 𝑑𝑥 𝑑𝑥 Unidad 2 La Integral como Antiderivada 2-31