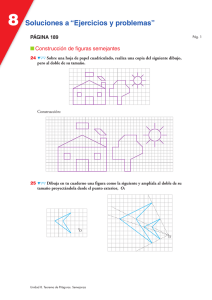
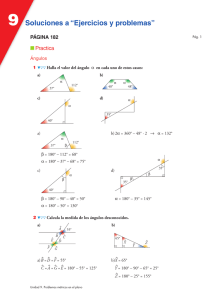
2. Ayuda a la resolución de problemas
Anuncio

UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 1 de 4 1 Tenemos tres copas de forma cónica de 6 cm de radio y 15 cm de altura. La primera está llena, en la segunda el líquido alcanza 10 cm, y en la tercera, 5 cm. Calcula la cantidad de líquido que contiene cada copa. 6 A 6 6 15 cm 10 cm 5 cm B AYUDA • Volumen de la primera V = π R 2 · h = … 3 • Para calcular el volumen de la segunda, necesitamos calcular el radio menor: 6 R1 De la semejanza de estos triángulos: R1 10 = 8 R1 = … 6 15 15 10 • Volumen de la segunda: V = π R 21 · 10 = … 3 • Repite el procedimiento anterior para hallar el radio y el volumen de la tercera. SOLUCIÓN π 2 6 · 15 = 565,49 cm3 3 V= R1 6 = V1 = R2 6 = V2 = 10 15 8 R1 = 4 cm π · 42 · 10 = 167,55 cm3 3 5 15 8 R2 = 2 cm π · 22 · 5 = 20,94 cm3 3 UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 2 de 4 2 Una maceta tiene forma de tronco de pirámide cuadrangular regular con las dimensiones que se indican en la figura. Calcula su volumen. 18 cm 20 cm 10 cm AYUDA V • Prolongamos las aristas laterales hasta que se corten para obtener la pirámide de la que se obtiene el tronco. • Tenemos que hallar la altura de la pirámide mayor VO', y de la menor, VO: A O D 10 cm — — AC = √102 + 102 = 10 √2 8 AO = … O A 10 B 20 cm A' C O' 18 cm D' C' — — A'C' = √182 + 182 = 18 √2 8 A'O' = … O' A' 18 B' • Por la semejanza de los triángulos AOV y A'O'V' se verifica: — — AV = AO 8 Obtén AV y A'V . A'V A'O' — — • Con el teorema de Pitágoras, halla las alturas VO y V'O. — — • Volumen del tronco = VPIRÁMIDE MAYOR – VPIRÁMIDE MENOR = 1 182 · VO' – 1 102 · VO = … 3 3 SOLUCIÓN — — — — — — AO = 5√2 cm; A'O' = 9√2 cm; AV = 25 cm; A'V = 45 cm; VO › 23,98 cm; VO' › 43,16 cm V = 3 861,95 cm3 UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 3 de 4 3 En un cono de 5 cm de radio y 12 cm de altura se inscribe una esfera. Calcula su radio. A R P O B 5 cm C AYUDA • Hallamos la generatriz del cono: — — — — AC 2 = BC 2 + AB 2 = 52 + 122 8 AC = … ì • Los triángulos ABC y APO son semejantes, por ser rectángulos con un ángulo agudo común, el A . • Por semejanza: Hipotenusa de APO = Cateto menor de APO Hipotenusa de ABC Cateto menor de ABC 8 AO = OP AC BC • Si llamamos R al radio de la esfera: — — — OP = R y AO = AB – R = 12 – R • Sustituye en la igualdad [1] y despeja R. SOLUCIÓN — AC = 13 cm 12 – R R = 13 5 ) 8 R = 3,3 cm [1] UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 4 de 4 4 Si cortamos un tronco de cono por un plano perpendicular a las bases la sección es un trapecio isósceles de bases 26 cm y 34 cm y altura 12 cm. Halla el volumen del tronco de cono. 26 cm 12 cm 34 cm AYUDA V Prolonga los lados laterales hasta llegar al vértice del cono y ten en cuenta la semejanza de los triángulos VAB y VCD: x = … x + 12 … x 13 A B 12 C 17 D SOLUCIÓN x 13 = 8 x = 39 cm x + 12 17 V= π 3 · 172 · 51 – π 3 · 132 · 39 = 8 532,57 cm3 UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 1 de 4 1 Tenemos tres copas de forma cónica de 6 cm de radio y 15 cm de altura. La primera está llena, en la segunda el líquido alcanza 10 cm, y en la tercera, 5 cm. Calcula la cantidad de líquido que contiene cada copa. 6 A 6 6 15 cm 10 cm 5 cm B AYUDA • Volumen de la primera V = π R 2 · h = … 3 • Para calcular el volumen de la segunda, necesitamos calcular el radio menor: 6 R1 De la semejanza de estos triángulos: R1 10 = 8 R1 = … 6 15 15 10 • Volumen de la segunda: V = π R 21 · 10 = … 3 • Repite el procedimiento anterior para hallar el radio y el volumen de la tercera. SOLUCIÓN π 2 6 · 15 = 565,49 cm3 3 V= R1 6 = V1 = R2 6 = V2 = 10 15 8 R1 = 4 cm π · 42 · 10 = 167,55 cm3 3 5 15 8 R2 = 2 cm π · 22 · 5 = 20,94 cm3 3 UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 2 de 4 2 Una maceta tiene forma de tronco de pirámide cuadrangular regular con las dimensiones que se indican en la figura. Calcula su volumen. 18 cm 20 cm 10 cm AYUDA V • Prolongamos las aristas laterales hasta que se corten para obtener la pirámide de la que se obtiene el tronco. • Tenemos que hallar la altura de la pirámide mayor VO', y de la menor, VO: A O D 10 cm — — AC = √102 + 102 = 10 √2 8 AO = … O A 10 B 20 cm A' C O' 18 cm D' C' — — A'C' = √182 + 182 = 18 √2 8 A'O' = … O' A' 18 B' • Por la semejanza de los triángulos AOV y A'O'V' se verifica: — — AV = AO 8 Obtén AV y A'V . A'V A'O' — — • Con el teorema de Pitágoras, halla las alturas VO y V'O. — — • Volumen del tronco = VPIRÁMIDE MAYOR – VPIRÁMIDE MENOR = 1 182 · VO' – 1 102 · VO = … 3 3 SOLUCIÓN — — — — — — AO = 5√2 cm; A'O' = 9√2 cm; AV = 25 cm; A'V = 45 cm; VO › 23,98 cm; VO' › 43,16 cm V = 3 861,95 cm3 UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 3 de 4 3 En un cono de 5 cm de radio y 12 cm de altura se inscribe una esfera. Calcula su radio. A R P O B 5 cm C AYUDA • Hallamos la generatriz del cono: — — — — AC 2 = BC 2 + AB 2 = 52 + 122 8 AC = … ì • Los triángulos ABC y APO son semejantes, por ser rectángulos con un ángulo agudo común, el A . • Por semejanza: Hipotenusa de APO = Cateto menor de APO Hipotenusa de ABC Cateto menor de ABC 8 AO = OP AC BC • Si llamamos R al radio de la esfera: — — — OP = R y AO = AB – R = 12 – R • Sustituye en la igualdad [1] y despeja R. SOLUCIÓN — AC = 13 cm 12 – R R = 13 5 ) 8 R = 3,3 cm [1] UNIDAD 11 La semejanza y sus aplicaciones 2. Ayuda a la resolución de problemas: triángulos semejantes en el espacio Soluciones Pág. 4 de 4 4 Si cortamos un tronco de cono por un plano perpendicular a las bases la sección es un trapecio isósceles de bases 26 cm y 34 cm y altura 12 cm. Halla el volumen del tronco de cono. 26 cm 12 cm 34 cm AYUDA V Prolonga los lados laterales hasta llegar al vértice del cono y ten en cuenta la semejanza de los triángulos VAB y VCD: x = … x + 12 … x 13 A B 12 C 17 D SOLUCIÓN x 13 = 8 x = 39 cm x + 12 17 V= π 3 · 172 · 51 – π 3 · 132 · 39 = 8 532,57 cm3