Trabajo Práctico N°4
Anuncio

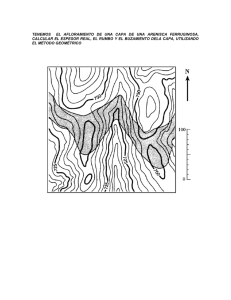
Departamento de Geología UNSL Trabajo Práctico N°4 Problema de los tres puntos Reconstrucción del diseño de afloramiento de estratos Objetivos: - Definir isohipsa estructural. Desarrollar el método de los tres puntos para cálculo de rumbo y buzamiento. Reconstruir patrones de afloramientos en base al método de los tres puntos en cartas topográficas. Elementos a utilizar: regla, trasportador, escuadra, lápices, calculadora, tijera, pegamento Isohipsas estructurales El entendimiento de isohipsa estructural o contorno de una estructura resulta básico en el uso de métodos cuantitativos, ya que muchas de las soluciones gráficas hacen uso de ellos. Las curvas de nivel o isohipsas topográficas son líneas que unen puntos de igual elevación en el terreno, generalmente proyectadas sobre un plano horizontal. Los contornos de estructuras o isohipsas estructurales, son proyecciones de líneas que unen puntos de igual profundidad o altura de un nivel geológico determinado sobre un plano horizontal (ej.: un estrato). En un estrato esquemático representado por un cuerpo tabular, los puntos MNOP conforman la superficie o techo buzante de la formación (Fig. 3.1). Las líneas segmentadas, unen puntos de igual profundidad ubicadas a intervalos o equidistancias de 100 metros, y coinciden con distintas líneas de rumbo contenidas sobre el techo del estrato. Las líneas continuas son su proyección sobre un plano horizontal, siendo los contornos de la estructura o isohipsas estructurales, de la superficie particular analizada. Todos los contornos de estructuras o isohipsas estructurales son coincidentes con líneas de rumbo en un sector determinado. Conociendo esto, es posible construir el actual buzamiento en profundidad a partir de un mapa de contorno de estructuras. isohipsas estructurales Figura 3.1 Block diagrama de un estrato buzante y sus isohipsas estructurales (líneas continuas), resultado de la proyección en un plano horizontal de líneas que unen puntos de igual profundidad del techo del estrato (líneas segmentadas). Las isohipsas siempre resultan paralelas al rumbo de la estructura. Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 1 Departamento de Geología UNSL En el ejemplo de la figura 3.2, se muestra un mapa de isohipsas esquemático y la representación de un perfil según la línea X-Y. El ángulo de buzamiento del plano puede ser ahora calculado en base a este perfil mediante trigonometría, utilizando el triángulo M-P-Y´. Figura 3.2 Mapa esquemático de isohipsas estructurales y un perfil del mismo según la línea X-Y. En el perfil se puede determinar el triángulo MPY’, con el cual se puede calcular el ángulo de buzamiento de la capa. Método de los tres puntos Este método permite resolver la obtención en forma geométrica el rumbo y buzamiento de estratos en base a cartas topográficas, con geometrías principalmente tabulares. Para tal finalidad es necesario contar con tres puntos del afloramiento de un mismo nivel estratigráfico (ej.: techo), con cotas perfectamente definidas. Como se mencionó anteriormente, resulta necesario hacer referencia a líneas de rumbo que son coincidentes con las isohipsas estructurales. Utilizando el método de los tres puntos se puede operar de dos formas: con dos puntos de igual elevación y uno diferente o con tres puntos de diferente elevación. 1- Tres puntos, dos de igual elevación: Sí existen dos puntos (A y C) de igual cota sobre un nivel de un estrato, la línea de rumbo es obtenida directamente por la conexión de los puntos por medio de una recta (Fig. 3.3).Una segunda línea de rumbo puede ser trazada paralela a la primera, con un tercer punto (B) que se encuentre a distinta elevación. El segmento comprendido entre estas líneas de rumbo constituye la equidistancia igual que para las curvas de nivel (Fig. 3.3). N Escala 1:20.000 Figura 3.3 Método de tres puntos, dos de ellos a igual elevación. Los puntos A y C se encuentran a la misma altura sobre el techo de un estrato, al unirlos se obtiene el rumbo. Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 2 Departamento de Geología UNSL Obtención del rumbo y buzamiento La figura 3.3 muestra que el rumbo obtenido es E-O. En, el buzamiento se obtiene usando un triángulo, el cual se rebate sobre el plano de la carta (Fig. 3.4a). Para la resolución gráfica, se unen dos líneas de rumbo contiguas con una recta perpendicular S-T (Fig. 3.4 a y b). Sobre la línea de rumbo de menor altura, se traza un segmento con origen en el punto T, de una longitud calculada en base a la equidistancia y la escala del mapa (Fig. 3.4b). Uniendo el extremo Z con el segmento trazado se obtiene el triángulo STZ. Utilizando un transportador se puede calcular gráficamente el valor. También puede realizarse el cálculo trigonométrico (Tgδ=ST/TZ) lo que permite corroborar la exacta construcción del gráfico: a. b. Figura 3.4 Método de tres puntos, resolución gráfica. a. Representación del problema en 3D. b. Representación en planta y cálculo del segmento TZ. 2- Tres puntos de distinta elevación: En este caso se deben conocer como mínimo tres afloramientos de igual nivel estratigráfico y distinta posición topográfica, por ejemplo los puntos A, B y C (Fig. 3.5a), en los cuales A es el de menor cota y C el de cota mayor. Entre la línea que une A-C existe un punto (P) que posee igual elevación que el punto B. Esta localización puede hacerse gráficamente, como se realiza en el caso de interpolación de curvas de nivel. Se mide la longitud del segmento entre A-C y se interpola mediante regla de tres simple, determinando así el punto P. La figura 3.5b muestra en tres dimensiones el mismo problema. Desde este punto, para la obtención del rumbo y buzamiento se procede de la misma manera que en el caso anterior. a. b. Figura 3.5 Método de tres puntos de diferente elevación: a. Solución del problema por método gráfico b. Representación tridimensional del problema. Consideraciones sobre el método de los tres puntos Se puede acotar que este método ofrece una ventaja invalorable en el trabajo de mapeo, ya que se puede conocer la actitud de formaciones con solo poseer tres puntos en una carta sin poseer limitaciones de escala o superficies. Entre las limitaciones más importantes se pueden mencionar que el geólogo debe conocer la polaridad de las capas donde se toman los puntos para la resolución gráfica, ya que los mismos deben ser referidos a un mismo nivel estratigráfico o estructural. Estos datos pueden ser difíciles de obtener si no se disponen de buenos afloramientos, lo que induciría a una interpretación errónea. Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 3 Departamento de Geología UNSL Predicciones de patrones de afloramientos Usando el método de los tres puntos se puede llegar a predecir el patrón de afloramiento de un estrato. La erosión que modela la topográfica puede originar diseños sinuosos en relación al buzamiento de la capa o estructura. La metodología para la reconstrucción consiste en proyectar sucesivamente las líneas de rumbo (Fig. 3.6), conservando la equidistancia obtenida. Como consecuencia de la actividad erosiva que genera una topografía irregular, el estrato puede aflorar en valles o crestas. Donde se intersecta una curva topográfica con una línea de rumbo de igual valor se debe observar un punto de afloramiento. En base a este criterio se puede predecir cada uno de los sectores en que aflora un estrato. Uniendo cada punto es posible determinar el patrón de afloramiento. En esta metodología el diseño esta estrictamente controlado por la topografía y las líneas de rumbo. Debido a esto la traza no se continua si no se intersecta una curva topográfica con la línea de rumbo correspondiente. En tal caso se debe realizar el trazado del afloramiento entre el último intervalo de las curvas de nivel. Si se cuenta con un punto del nivel estratigráfico complementario (ej.: base y techo) y asumiendo al estrato uniformemente buzante y su espesor constante, se traza la línea de rumbo paralela a la anterior, trasladando desde la misma el valor de la equidistancia obtenida por los tres puntos. Con esta traza se obtiene el diseño completo del afloramiento (techo y base). Puede ocurrir que no se cuente con el afloramiento correspondiente al nivel complementario, pero sí el espesor vertical o verdadero, entonces con este valor se puede reconstruir de igual manera el diseño de afloramiento. Figura 3.6 Predicción de patrones de afloramiento, en base al método de tres puntos en una carta topográfica. Los puntos A-B-C, corresponden a un mismo nivel estratigráfico de los cuales se obtiene el rumbo de la capa. El punto D, corresponde a otro nivel de la misma capa. Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 4 Departamento de Geología UNSL Planos geológicos, topografía e isohipsas Diferentes ejemplos de casos de contactos planares, topografía e isohipsas y su representación. Se recomienda utilizar como herramienta de comparación con la ejercitación propuesta anteriormente. a. Buzamiento opuesto a la pendiente topográfica: 1.Horizontal, 2.Bz 9 NO, 3.Bz 17 NO, 4.Bz 32 NO Observar el diseño de afloramiento del contacto genera una V cuando cruza valles e interfluvios. 1. Bz 52º NO; 2. Bz 68º NO; 3. Bz 79º NO, curva de nivel cada 200m; 4. Bz 90º Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 5 Departamento de Geología UNSL b. Buzamiento con orientación similar a la pendiente topográfica: 1. Horizontal, 2.Bz 9 SE, 3.Bz 17 SE, 4.Bz 32 SE 1. Bz 52º SE; 2. Bz 68º SE; 3. Bz 79º SE, curva de nivel cada 200m; 4. Bz 90º Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 6 Departamento de Geología UNSL Trabajo Práctico N° 4 Método de los tres puntos Alumno: Fecha: Ejercitación Ejercicio N° 1 Los puntos A, B y C corresponden a un contacto entre litologías diferentes (mismo nivel estructural). Por el método de los tres puntos reconstruir el afloramiento, determinar el rumbo y buzamiento y trazar perfiles paralelos y perpendiculares a la estructura. N E 1:20.000 Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 7 Departamento de Geología UNSL Ejercicio N° 2 En la siguiente carta topográfica los puntos A, B y C corresponden a un contacto entre litologías diferentes (mismo nivel estructural) y D corresponde al nivel complementario de la misma capa. Por el método de los tres puntos reconstruir el afloramiento, determinar el rumbo y buzamiento. Trazar un perfil paralelo y un perfil perpendicular a la estructura. D A C N B E 1:20.000 Ejercicio N° 3 En la siguiente carta topográfica los puntos A, B y C corresponden a un contacto entre litologías diferentes (mismo nivel estructural). Por el método de los tres puntos reconstruir el afloramiento, determinar el rumbo y buzamiento Trazar un perfil paralelo y un perfil perpendicular a la estructura y ordenar la secuencia sedimentaria. N Pelita Arenisca B A C Arenisca Caliza E 1:25.000 Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 8 Departamento de Geología UNSL Ejercicio N° 4 El siguiente es un modelo 3D en papel con el planteo de un problema de los tres puntos (ABC). Recortarlo y ensamblarlo. Calcular el buzamiento real en base a los datos que puede extraer del modelo Geología Estructural 2014 UNSL Geología Estructural 2014 - Trabajo Práctico N° 4 – Problema de los tres puntos 9