Experimento de Hafele y Keating

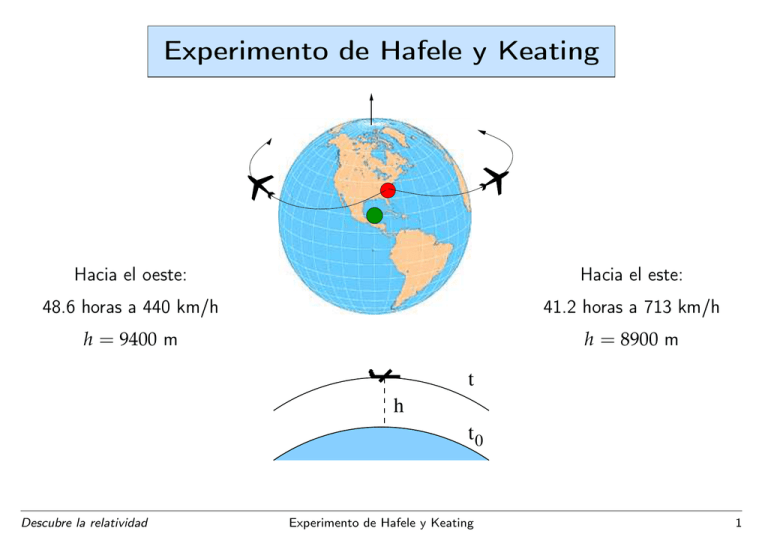
Experimento de Hafele y Keating
Hacia el oeste:
Hacia el este:
48.6 horas a 440 km/h
41.2 horas a 713 km/h
h = 9400 m
h = 8900 m
t
h
t0
Descubre la relatividad
Experimento de Hafele y Keating
1
Experimento de Hafele y Keating
Dilatación cinemática t• ≡ t0 = Centro de la Tierra, t• ≡ t A = Aeropuerto
v A = ωR cos α,
ωR = 1675 km/h = 465 m/s,
α = latitud (supondremos α = 0◦ )
• Hacia el Este: t0 = γ(v A )t A = γ(v A + v E )t E
v2A
( v A + v E )2
t0
t0
= t0 1 − 2 ,
= t0 1 −
⇒ tA =
tE =
γ(v A )
2c
γ(v A + v E )
2c2
t0 2
2
⇒ ∆t E = t E − t A = − 2 (v A + v E ) − v A = −184 ns (retrasan)
2c
• Hacia el Oeste: t0 = γ(v A )t A = γ(v A − vW )tW
2 2
v
t0
t0
(v − v )
⇒ tA =
= t0 1 − A2 ,
tW =
= t0 1 − A 2 W
γ(v A )
2c
γ ( v A − vW )
2c
t0 2
2
⇒ ∆tW = tW − t A = 2 v A − (v A − vW ) = 96 ns (adelantan)
2c
v2
• Nota: Si viajaran a v v A siempre retrasarían: ∆t = −t0 2 < 0
2c
Descubre la relatividad
Experimento de Hafele y Keating
2
Experimento de Hafele y Keating
2GM
Nota:
= 9 mm R = 6370 km
c2
Dilatación gravitatoria
t = t0 1 −
= t0
2GM
c2 ( R + h )
1/2 1−
2GM
c2 R
−1/2
' 1−
GMh R
gh R
1+ 2 2
= t0 1 + 2
c R R+h
c R+h
Descubre la relatividad
GM
c2
⇒
1
1
−
R+h R
gh R
∆t = t − t0 = t0 2
>0
c R+h
hE
⇒
∆t E = 144 ns (adelantan)
hW
⇒
∆tW = 179 ns (adelantan)
Experimento de Hafele y Keating
3
Experimento de Hafele y Keating
Efecto total (errores estimados en el artículo original)
Diferencia de tiempos
Hacia el este
Hacia el oeste
Dilatación cinemática
−184 ± 18 ns
96 ± 10 ns
144 ± 14 ns
179 ± 18 ns
Efecto total
−40 ± 23 ns
275 ± 21 ns
Efecto observado
−59 ± 10 ns
273 ± 21 ns
Dilatación gravitatoria
Descubre la relatividad
Experimento de Hafele y Keating
4
Relojes en órbita
Orbitación
⇒
v2
r
GMm
=m
2
R+h
( R + h)
Es una velocidad muy grande: h = 0
⇒
⇒
v=
GM
R+h
v = 8 km/s = 28 800 km/h ωR
• Dilatación cinemática:
t0 v2
gR R
∆t|cin = −
=
−
t
0 2
2 c2
2c R + h
• Dilatación gravitatoria:
∆t|grav = t0
gh R
c2 R + h
• Ambos efectos tienen signo contrario:
R
– Si h = h? = = 3185 km se cancelan
2
– Si h < h? domina efecto cinemático (retrasan)
– Si h > h? domina efecto gravitatorio (adelantan)
Descubre la relatividad
Relojes en órbita
5
Relojes en órbita
ISS Estación Espacial Internacional
Orbita a h = 340 km < h? ⇒ v = 7.7 km/s = 27 700 km/h
∆t|cin = −28.5 µs/día
∆t|grav = 3.2 µs/día
∆t|tot = −25.3 µs/día (retrasan)
GPS
Orbitan a h = 20 000 km > h? ⇒ v = 3.9 km/s = 14 000 km/h
∆t|cin = −7.2 µs/día
∆t|grav = 45.4 µs/día
∆t|tot = 38.2 µs/día (adelantan)
Descubre la relatividad
Relojes en órbita
6